一种线性规划的铁心纵剪排片方案计算方法

李 艳，贾振楠，文 松，刘仁峤

（1.江西变压器科技股份有限公司，江西 南昌 330314；2.南昌大学，江西 南昌 330031）

0 引言

变压器铁心的各级硅钢片，是将一定尺寸的硅钢片卷料（硅钢卷）纵剪，得到各级硅钢片的卷料后，再横剪得到。硅钢片作为变压器生产所需的主要原材料之一，其质量占整台产品总质量的1/3～1/4，费用占整台产品总物耗的30%以上。在一次生产任务中，如何使用最少量的硅钢卷而纵剪得到所需要的各级硅钢片卷料，是非常有意义的问题。它能帮助我们降低硅钢卷的采购量。而硅钢卷的低采购量意味着低成本、低库存[1-3]。

文中提出一种基于线性规划的铁心纵剪排片计算方法。该方法将铁心纵剪描述成一个线性规划最小化问题，并利用成熟的单纯型算法，快速得到一个最优解，从而给出一个相应的铁心纵剪排片方案。该方案能满足生产所需且硅钢卷用量最小[4-7]。

1 铁心纵剪问题描述及数学建模

为了将问题简化，这里忽略实际生产中对硅钢卷的料头料尾的处理。问题也简化为：如何安排纵剪，使得所用硅钢卷的长度最短。

如何安排纵剪，这涉及到宽度、长度两个方向上的问题，在宽度方向上，有（d1，d2，d3，…，di，…）共n个所需硅钢片的宽度要通过硅钢卷的宽度（d）裁剪而来，显然，硅钢卷的宽度必须大于等于任何一个所需的硅钢片宽度

d≥di

大多数时候我们可以找到满足

ci1×di1+ci2×di2+…≤d

且满足

ci1×di1+ci2×di2+…≤d

的宽度组合，式中dik为n个宽度中的任意一个宽度，mm；Cik为组合中宽度dik的个数。现举例说明：有宽度为1 020 mm的硅钢卷，硅钢片的宽度有：300 mm，350 mm，390 mm等，其中300 mm是的最小宽度，那么可以很容易找到以下几个满足条件的宽度组合：

1）（2×390）mm=780 mm（余240<300）

2）（390+350）mm=740 mm（余280<300）

3）390 mm+（ 2×300）mm=990 mm（余 30<300）

4）（2×350）mm+300 mm=1000 mm（余 20<300）

5）350 mm+（2×300）mm=950 mm（余 70<300）

如上所示，当n较小时，组合的数量不多，仅凭人工依序组合也是轻而易举，但随着n的增大，组合数会急剧增加到几千甚至是几万的量级。因而为了得到所有满足条件的宽度组合，要使用递归的方法，具体算法如图1所示。

图1 宽度组合算法流程图

设满足条件的宽度组合有m个，由于任何一个硅钢片的宽度都不大于硅钢卷的宽度，所以对于每一种宽度都会至少存在一个宽度组合包含它。对于这样一个组合问题，m远大于n，那么数量如此多的组合要如何取舍？考虑到长度方向上必须要满足的条件：裁剪所得各宽度硅钢片的总长度不能低于其所需长度（l1，l2，…，li，…），且我们对母材硅钢卷的目标也是其长度最短，此时，不妨就将各宽度组合的裁剪长度设为自变量Xj，于是

式中Cij为宽度为di的硅钢片在第j个组合中所占的个数，组合中不包含宽度为di的硅钢片时Cij=0。也可以很容易得到所用母材硅钢卷总长即为各组合长度的和，于是

由于组合长度不可能为负，所以上两式中

Xj≥0

纵观以上分析，不难看出，这是一个线性规划最小化问题：

最小化

满足约束：

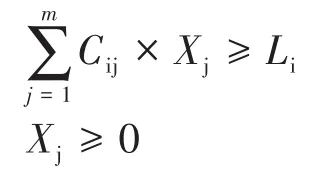
2 利用线性规划的单纯型算法求解

2.1 单纯型算法

要求模型转化为线性规划的标准型，得到

满足约束：

最大化：

2.2 约束条件和目标函数的处理

在实际计算中，通常将约束条件的左边构造为一个m×n的矩阵A=（aij），右边构造为一个m维的向量b=（bi），将目标函数的系数构造为一个n维向量c=（cj），重写数学模型得到

最大化

CTx

满足

Ax≤b

x≥0

计算时，输入矩阵A和向量b、c作为参数，即可求得向量x。

3 系列产品算例

现有某系列产品的硅钢片需求表，试用根据本方法编写的铁心纵剪优化软件对其进行纵剪计算。其中硅钢卷片宽为980 mm，硅钢片需求表及计算结果如表1、表2。

表1 某系列产品的调变硅钢片需求表 mm

表2 利用铁心纵剪优化程序得出的组合方案详情mm

算例中单边裁边宽为5，宽度组合共40 334种。

4 结语

硅钢片纵剪排片不是一般的数学问题，而是一个比较复杂的工程问题，它既在宽度方向上有一个组合问题，又在长度方向上有一个排列问题，就一个系列的变压器而言，其排列组合之多，以人工之力，是无法在生产计划能接受的时间内穷尽并得出一个最优方案的，即使通过计算机编程，穷尽法也不可取。

而此基于线性规划的排片方法，利用已成熟的单纯型算法，可快速求得最优解，给出一个硅钢卷采购量最小的纵剪排片方案。