哈密顿表象中的投影算子及性质分析①

徐丽雯， 张海丰， 刘明达， 韩海生， 李慕勤

(佳木斯大学a.理学院,b.附属第二医院,c.材料科学院，黑龙江 佳木斯 154007)

0 引 言

在量子力学中，哈密顿算符表象是很重要的基本表象之一，很多体系的哈密顿算符本征值问题的求解都是在哈密顿算符表象下进行的，因而在大量的研究中被使用，例如：张鹏程等在哈密顿算符表象中对一维谐振子做了计算[1]；李重石给出了三维谐振子哈密顿算符表象下径向矩阵元的简要形式[2]；韩菊等在坐标表象和哈密顿算符表象中对电场中带电谐振子进行了求解[3]；马春生等在哈密顿算符表象中使用应变补偿对多量子阱价带结构哈密顿方程进行了求解。此外，投影算子也在国内外的量子体系研究中被大量的应用[5-8]。

1 哈密顿算符表象

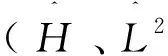
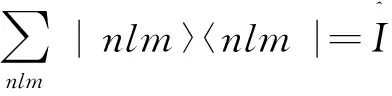
(1)

任意波函数向该本征函数系基矢投影后就得到了哈密顿算符表象下的波函数。任意波函数|ψ〉向该表象投影可得

(2a)

展开项系数{Anlm}就是波函数|ψ〉在该表象下的表示形式。

易知(2a)式在坐标表象中为

(2b)

相应展开系数可以表示为

(2c)

2 哈密顿算符表象中的封闭关系

于是，对于任意的态函数|ψ〉可以由于正交归一系的基矢表示为

(3)

其中，展开项系数表示为

cn=〈n|ψ〉

(4)

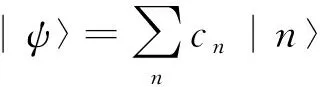
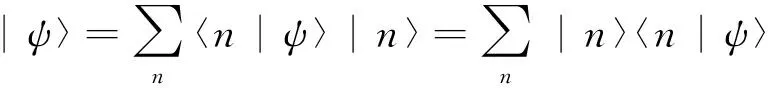
(5)

可见，应该有下式成立

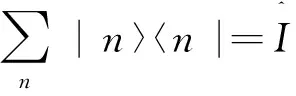
(6)

这体现了基矢{|n〉}的完备性的表现，即封闭关系，由于其等于1，所以它可以任意插入到公式的任何位置。

3 投影算子

(7)

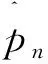
(8)

3.1 去n态投影算子

根据上边投影算子的定义，若令

(9)

令其作用在任意一个态矢|ψ〉上，则有

(10)

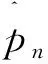
3.2 投影到|m〉态的投影算子

根据投影算子的定义，可以做如下定义

(11)

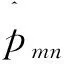
(12)

4 投影算子的性质及应用

4.1 投影算子和哈密顿算符的对易

取任意态矢|ψ〉，有

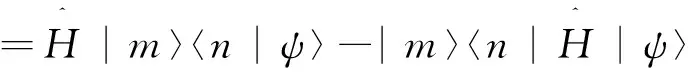
(13)

所以

(14)

4.2 投影算子的性质

(15)

4.3 投影算子的迹

(16)

4.4 任意算符在哈密顿算符表象中的表示

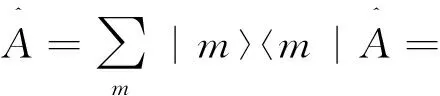
(17)

而

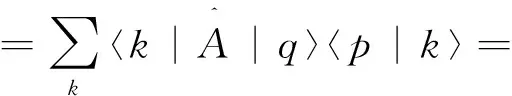
(18)

5 结 论