高中生数列学习障碍及其成因的调查研究

2020-12-28张玉娟

鞍山师范学院学报 2020年6期

张玉娟,张楠,刘兵

(鞍山师范学院数学与信息科学学院,辽宁鞍山 114007)

高中数学知识与初中数学知识相比更抽象、逻辑性更强且内容更丰富.高中生存在数学学习障碍已经成为普遍现象[1]，数列作为高中数学极为重要的一部分，学生在实际的学习中存在着很多问题，这些问题如果不解决，不仅会影响学生后续数学知识的学习，还会影响其他学科的学习[2].因此，数列学习障碍的研究成为一个亟待解决的问题.本研究根据梁威教授对数学学习障碍的分类[3]，结合高中数学课程标准以及高考大纲对数列的要求，将数列学习障碍分为概念理解障碍、运算障碍、公式与性质应用障碍以及数学思想方法应用障碍来进行研究.

1 学习障碍的概念

学习障碍最早是由美国的特殊教育学家Kirk于20世纪60年代初提出[4]，由于学习障碍的复杂性，至今对学习障碍还没有一个统一的定义.

1.1 学习障碍概念的界定

1981年，学者们反对用心理上的异常来定义学习障碍，给出了新的定义，把在听、说、读、写、推理或数学等方面表现出的显著困难用来代替心理异常这种提法[3].苏联教育界对学习障碍概念的研究主要持两种观点，第一种观点认为学习障碍就是代表智力发展落后；第二种观点认为学习障碍是“学业不良”[5].本文的学习障碍是指学习异常者，主要包括在听、说、读、写、推理和数学能力的获取和运用上有很大的困难，这里需要强调的是这些存在学习障碍的人智力正常.

1.2 数学学习障碍概念的界定

数学学习障碍是学习障碍的学科化，数学学习障碍普遍定义为：因为数学能力的欠缺而导致学生在数学学习上落后，学习成绩明显落后于同年级平均水平，表现为数学领域的学习障碍.

本文将数列学习障碍定义为：智力正常，因为数学能力的欠缺而导致学生在学习数列上落后，学习成绩明显落后于同年级平均水平的现象，表现为数列学习方面的学习障碍.

2 样本选取

2.1 研究对象

选取鞍山市某中学高二年级136名学生为研究对象，对他们的数列学习情况进行测试，分析他们在数列学习中存在的障碍.试卷发放时间选在数列月考之后，共发放试卷136份，有效试卷132份，试卷回收率为97%.

2.2 测试卷

测试卷共有7个题目，每题10分，满分为70分，测试卷的具体题目如下：

第1题已知数列{an}的前n项和Sn=2n2-30n，

(1)求出这个数列的通项公式;

(2)求出使得Sn最小的序号n的值.

第2题等差数列{an}的前n项和为Sn,

(1)Sk=10,S2k=40,求S3k；

(2)Sn,S3=9,S6=36，求a7+a8+a9；

第3题已知等差数列{an}中，Sn是它的前n项和，若S16>0,且S17<0,则当Sn最大时n的值是多少？

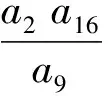
第5题在各项均为正数的等比数列{an}中，若a5=5,则log5a1+log5a2+…+log5a9的值是多少？

第6题已知等差数列{an}满足：a3=7,a5+a7=26,{an}的前n项和为Sn，

(1)求An及Sn；

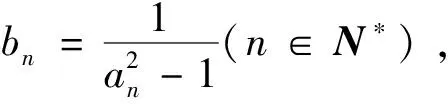
第7题已知{an}是首项为19，公差为-2的等差数列，Sn为{an}的前n项和,

(1)求通项an及Sn;

(2)设{bn-an}是首项为1，公比为3的等比数列，求数列{bn}的通项公式及其前n项和Tn.

2.3 测试卷的信效度

在测试前利用SPSS(19.0)软件对测试卷进行信效度分析，得到测试卷的信度如表1所示，测试卷的效度如表2所示.

表1 可靠性统计

由表1可以看出，该测试卷的信度为0.806，处于0.75～0.9之间，说明测试卷具有良好的信度；由表2可知，效度为0.701，大于0.5，说明测试卷具有良好的效度.根据测试卷先分析数列学习障碍的类型，再分析不同类型障碍的成因.

表2 KMO 和巴特利特检验

3 数列学习障碍类型的分析

对回收的132份试卷进行仔细批阅，再用Excel对试卷得分进行统计分析，具体情况如表3所示.

由表3可以看出，学生测试卷平均成绩只有36.31分.平均正确率为31%，也就是说大约70%学生在数列学习方面存在障碍，具体分析如下：第1题和第7题得分率最高，但是正确率却不高，说明只有少数学生能完全答对，而大部分学生只能部分答对.第5题考查了等比数列等比中项的性质与对数运算相结合的题目，得分率与正确率相近，说明学生在此题得分波动很大.第4题考察了等比数列与方程的结合，并融入了分类讨论思想，本题的正确率最低，说明学生在数学思想应用方面存在着普遍的障碍.

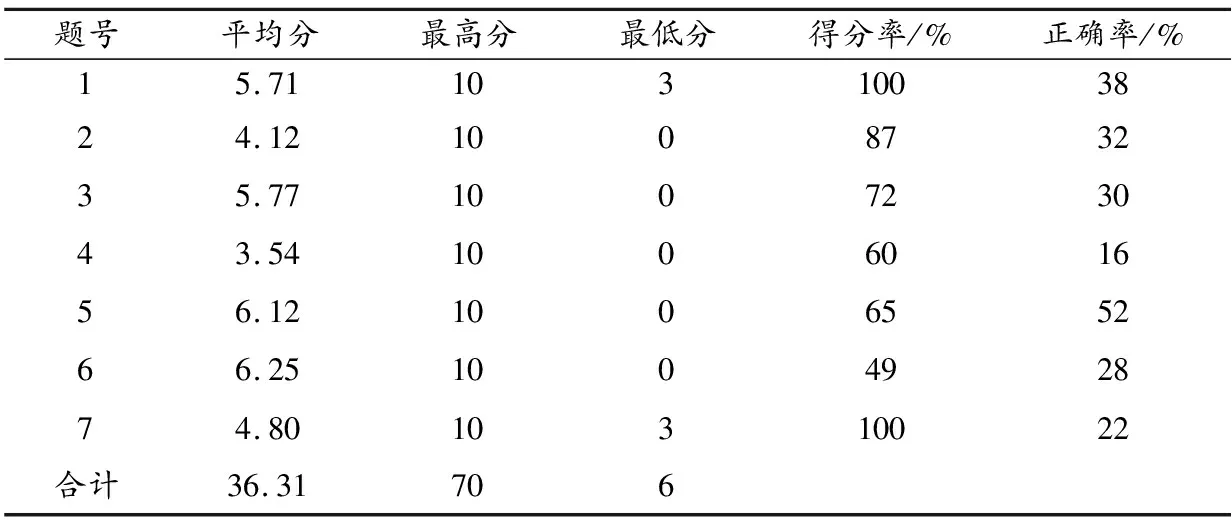
表3 测试卷得分情况统计表

根据梁威教授对数学学习障碍的分类对数列学习障碍进行如下研究：

3.1 概念理解障碍

概念理解障碍包括没有掌握数列所使用符号，对等差、等比数列的概念理解不到位.

测试卷第6题和第7题考察了数列的综合运用能力，学生需要把非等差、等比数列转化为等差、等比数列进行求解，学生只有对等差、等比数列的概念充分理解了才能求解.从统计结果看，较多学生没有得满分，甚至一些学生出现卷面空白的情况.通过对存在问题的部分学生访谈发现，多数学生不知道如何解题，很多同学对数列概念记忆不清，尤其是学习了数列的函数性质后.因此，一些学生在学习数列时存在概念理解障碍.

3.2 运算障碍

通过批阅测试卷发现，在数列的学习中很多学生存在计算错误.运算能力是数学能力的基础，也是高中生应该具备的数学核心素养之一.数列解题过程的每一步都考察学生的运算能力，数列的大部分题目看似简单，但事实并非如此.数列的很多题目中，运算量都不小，只要一步出错，则结果就错了.

根据学生测试卷的答题情况可以看到，学生的运算存在很大问题，大部分在数列学习中存在障碍的学生明明解题思路没问题，但是因为计算错误而拿不到分数.可见，学生在数列学习中存在运算障碍.

3.3 公式与性质应用障碍

数列解题过程中都会用到数列的公式与性质.如果数列的公式与性质不能准确地记忆，将会影响整个问题的解决.通过测试卷的答题情况可以看出，学生对基本的公式掌握得很好，而数列的性质掌握得不好，尤其是等差、等比数列的前n项和的性质掌握得不好.测试卷第2题考查了等差数列的前n项和的性质，学生的答题情况并不好，一些卷面出现空白.可见，在数列的学习过程中，学生在公式与性质的应用上也存在着障碍.

3.4 数学思想方法应用障碍

数学思想方法的掌握是数学学习极为重要的一部分.在数列的学习过程中，融入了很多数学思想方法，其中最为重要的三个数学思想方法是：函数思想、分类讨论思想、转化与化归思想[6].在新教材中，将数列作为一种特殊的函数来进行讲解，用函数的概念、性质等来解决数列问题；分类讨论思想用来解决数列中不能统一求解的问题，比如，测试卷第1题考察了利用数列前n项和求数列的通项公式，就用到了分类讨论思想；对于非等差、等比数列的相关问题，就要用到转化与化归思想，把它们转化为等差、等比数列来进行求解.思想方法的运用在解决数列综合问题时极为重要.

根据测试卷的答题情况可以看出，第1题、第4题、第6题和第7题均存在着思想方法的运用.尤为突出的是第4题，这道题考察了等比数列中的分类讨论思想的应用，大部分学生存在问题，由此可见，学生在学习数列的过程中对数学思想方法的应用存在着很大的问题.

4 数列学习障碍成因分析

4.1 概念理解障碍成因

在分析学生数列概念障碍的时候，通过翻看数列学习存在障碍学生的练习册，发现他们对一些基础知识掌握得不牢固.造成基础知识掌握不牢固的原因有很多，研究发现最大的原因是学生在学习数列的概念时不注重数列概念的形成分析，只对数列概念死记硬背，导致对数列概念理解不深刻，以至于在一些基础题目的变式上出错率较高.

数学是一门逻辑思维严谨的学科，教学内容的设计是层层递进的.虽然数列是学生在高中时才开始接触，但是在高中以前他们已经接触过找规律的题目，这类题目与数列的学习有着密不可分的关系.因此，基础知识薄弱的同学也会出现概念理解障碍.

4.2 运算障碍成因

数学运算是学生学习数学时必须具备的一种素质和关键能力.在数列的解题中，需要进行大量的运算.研究发现学生在面对复杂的运算时，存在着畏难的情绪，有的学生因为考试紧张，会出现暂时遗忘知识点的情况，甚至基础的移项、合并同类项、去括号等简单步骤也会出错.教师讲课时大都注重学生其他数学能力的培养而忽视运算能力的培养，因为课时少，教师讲题时会省略一些中间步骤，学生只听不做，这样使得一些运算不准确的学生在一些基础题目上丢分.长此以往，这些因素就使学生形成了不良的学习习惯，运算能力逐渐下降，从而造成了学生数列学习的运算障碍.

4.3 公式与性质应用障碍成因

在数列的学习中，出现了许多新的公式与性质.学生由于对公式与性质不理解，在记忆这些公式与性质时也就存在很多困难.数列的题型有着数字多、限制条件也多的特点，特别是一些变式题，学生不知道该用什么公式或性质求解.数学作为一门实用性学科，常常与实际生活相联系，很多数列的题目也和实际生活有关，学生无法将现实问题用数学符号准确地表示出来，从而导致学生对这类题不会求解.这些原因导致学生在公式与性质应用上出现障碍.

4.4 数学思想方法应用障碍成因

在数列概念掌握的基础上学生才能运用数学思想方法，而数列解题时，数学思想方法应用存在障碍的学生多数对数列概念的理解不深入.例如，测试卷的第1题考察了学生的分类讨论思想和函数思想，学生需要掌握数列项的概念才能知道为什么要进行分类讨论，同时类比二次函数最值问题，学生才会求解等差数列前n项和的最值问题.在平时的教学中，教师只是教学生如何解题，而不强调所用的数学思想方法，使得学生将自己的错误归咎为粗心大意、马虎、运算不准.久而久之，学生在学习数列时便存在数学思想方法应用障碍.