五十铃某发动机用增压器低周疲劳分析
2020-12-28高群芳邱济宝沃鸣杰
高群芳,邱济宝,沃鸣杰
(1.江西五十铃发动机有限公司,江西南昌 330200;2.宁波威孚天力增压技术股份有限公司,浙江宁波 315032)
0 引言
疲劳是引起工作结构和构件失效的最主要的原因。疲劳破坏是材料、零件和构件在循环加载下,在某点或某些点产生局部的永久性损伤,并在一定循环次数后形成裂纹、或使裂纹进一步扩展直到完全断裂的现象。任何材料都会发生疲劳破坏,因此在设计零部件及工程结构等时必须考虑到材料遭受疲劳破坏的时限,以免造成不必要的财产损失和人身伤亡事故。
涡轮增压器在使用过程中转速连续变化且无规律,而且增压器叶轮的基材一般为铝,强度较弱,叶轮主要承受离心力的作用力[1],而叶轮设计从气动性能考虑,叶轮叶片应尽可能地薄,使叶轮的工作应力非常大,因此叶轮的低周疲劳失效是增压器面临的较大的失效风险。
随着有限元软件及计算机技术的发展,使叶轮低周疲劳的计算分析成为可能。
本文作者针对五十铃某发动机用增压器项目,根据增压器负载主要考虑离心应力对压气机叶轮进行低周疲劳计算分析,以排除该机型的低周疲劳风险。
1 低周疲劳载荷的说明
低周疲劳发生的条件是承受扰动载荷,所谓扰动载荷是随时间变化的应力[2]。对于压气机叶轮载荷就是增压器转速引起的离心应力。
描述载荷-时间变化关系的图,称为载荷谱[3]。图1为客户提供的增压器200 km的载荷谱(数据为格尔木高原采集的数据)。
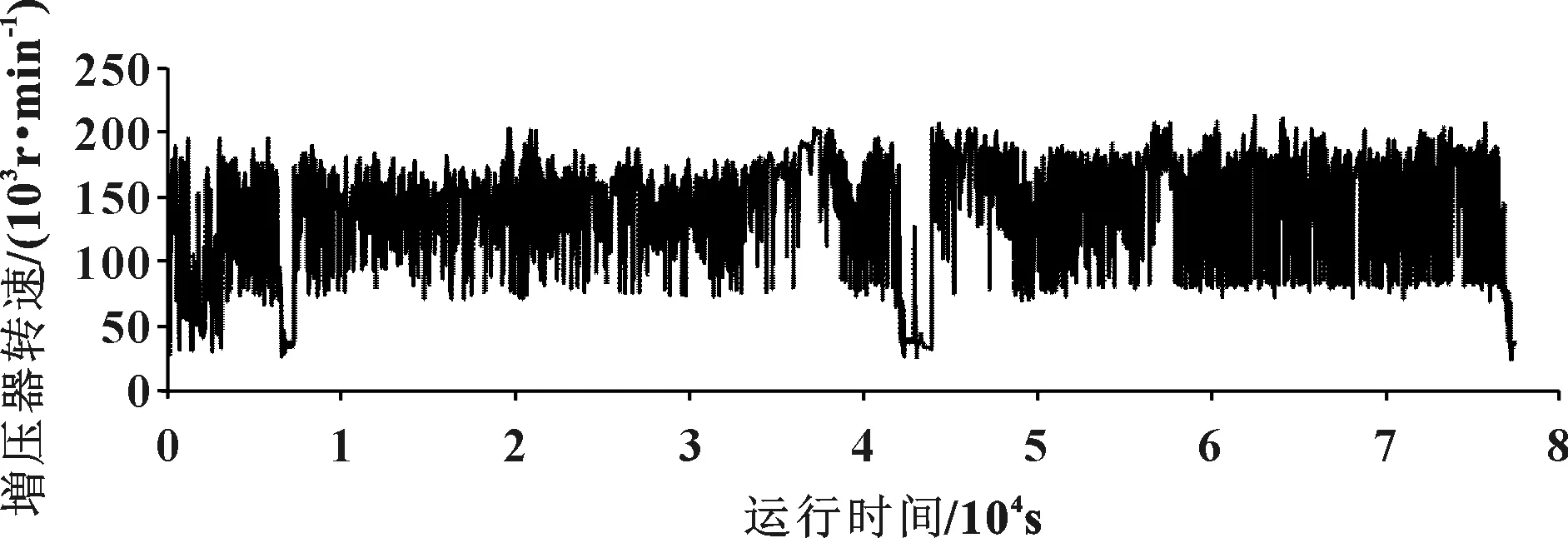
图1 200 km增压器载荷谱
需要根据客户提供的数据,计算载荷并判断压气机叶轮是否能满足发动机20万km的要求(高原地区要求)。
将连续的载荷-时间方程离散成一系列的峰值和谷值,并进行循环计数统计处理的方法称为“循环计数法”[3]。由于目前计算机能处理大量的数据,并不需要将载荷完全地分解成若干分段的载荷进行分别计算,只需要将原载荷的数据进行适当地简化用于减少计算量,如图2所示。
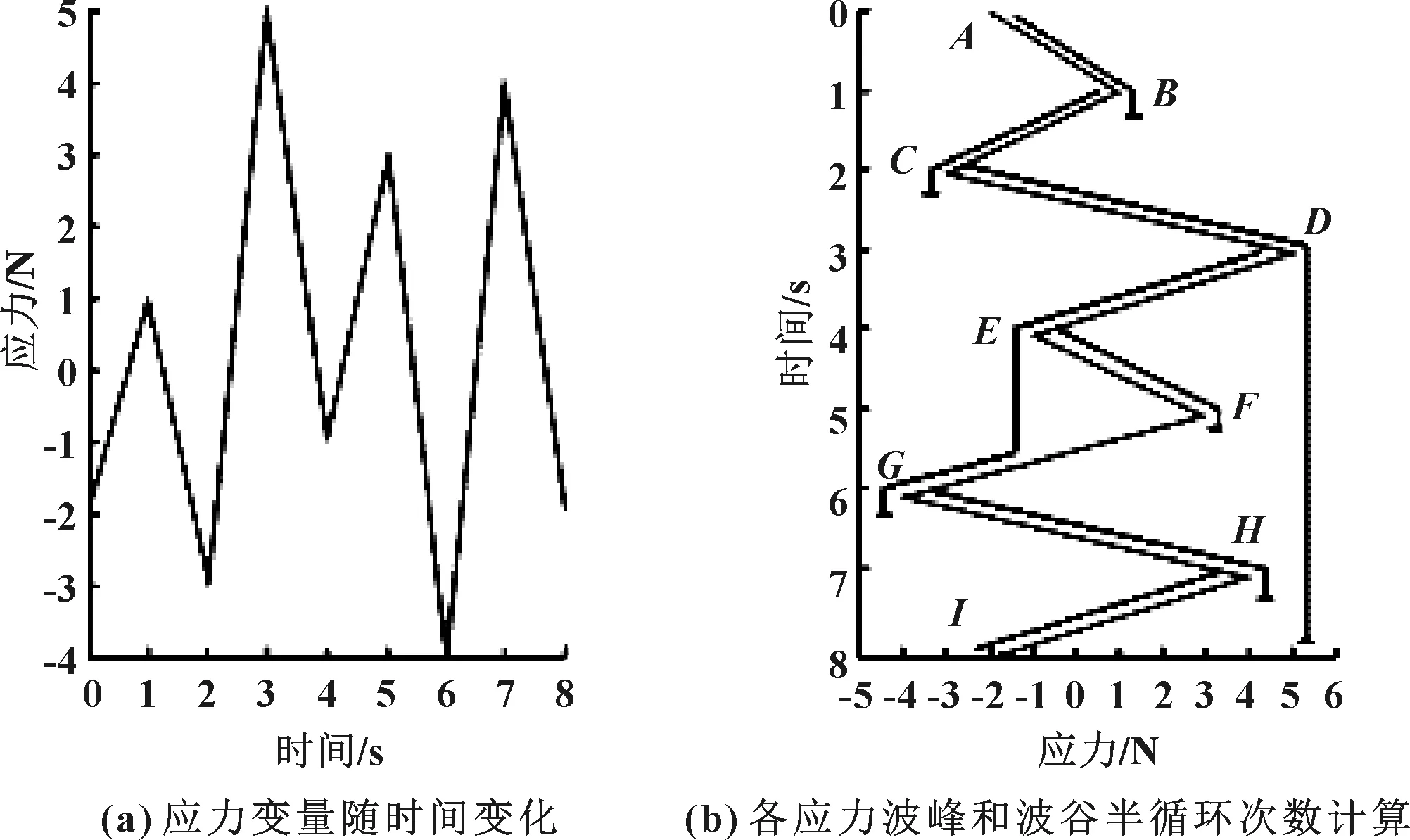
图2 一次雨落法进行载荷简化
通过编程将一次雨落法程序化,可以方便将采集的转速数据进行简化,如图3所示,由原来的近80 000次的计点减少为8 000次,减少了近9/10,极大地减少了计算机的计算时间。

图3 简化后的增压器转速循环曲线
2 S-N曲线
S-N曲线,也叫应力与寿命曲线,是以疲劳寿命的对数值lgN为横坐标,以材料标准试件疲劳强度为纵坐标、表示一定循环特征下标准试件的疲劳寿命和疲劳强度之间的曲线。材料的疲劳寿命一般是把原材料做成圆棒状,在特定的加工精度和热处理工艺下的标准样件,经过拉、压、弯曲以及扭转作用下得到的。疲劳强度是指材料在无限多次变更载荷作用而产生破坏的最大应力。目前对于增压器用的锻铝材料2618的S-N曲线国内没有相关疲劳数据,特别在高温下的数据,所以需要依据材料的强度Su作简单的估计,供设计参考。
S-N曲线计算表达方式为:
Sm·N=A
(1)
两边取对数得:
mLgS+ LgN=A
(2)
当寿命N=1时,S1=Su,反映试件在极限强度下被破坏或屈服。由于S-N反映的是长寿命疲劳,所以假设当寿命N=103
则S103=0.9Su
(3)
由于疲劳极限是由试验确定的,试验又无法无限制一直做下去,故在许多试验研究基础上,所谓的无穷大一般定义为:
对于金属材料,N=107次。
由于疲劳极限Sf存在误差,
所以假设当N=106时,则
S106=Sf=kSu
(4)
式中:k为反映不同载荷作用的形式系数。
综上所述:S-N曲线表达式为
A=m(0.9Su)m×103=m(kSu)×106
(5)
由上述计算式推出不同温度下增压器叶轮材料2618的S-N曲线,如图4所示。

图4 不同温度下2618的S-N曲线
3 不同应力幅值的等寿命转换
当应力幅值Sa=-1时,测得的S-N曲线为基本S-N曲线,则将实际应力等寿命转换为Sa=-1才能估计寿命。不同方式的等寿命条件如图5所示。

图5 不同方式的等寿命条件
由图5可知在等寿命条件下:
图5(c)中的抛物线为Sa-Sm关系的一种表达形式为
(Sm/Su)2+ (Sa/S-1) = 1
(6)
上述曲线被称为Gerber曲线[3],根据在整车上测得的实验数据,发现所有的数据点基本上在此抛物线附近。
图5(b)中的直线为Sa-Sm关系的另一表达形式,即
(Sa/S-1) + (Sm/Su) = 1
(7)
上述直线称为Goodman直线[3],发现所有的数据点基本都在这一直线的上方。
由于直线的表达形式简单,偏于保守,在实际工程中常用,所以现在采用Goodman方式。
4 Miner线性累积损伤理论
在实际工作中,受到的载荷是变化的,体现为扭矩和速度是变化的,不同挡位所使用的频繁程度即每挡所用时间也不相同,三者之间对应关系,就是载荷谱。载荷-循环次数图可以通过计数由载荷谱得到。
若构件在某恒幅应力水平S作用下,循环至破坏的寿命为N,则循环至n次时的损伤定义[3]为:
D=n/N
(8)
如n=0,则D=0,那么构件无疲劳损伤;
如n=N,则D=1,那么构件产生疲劳损伤。
D随循环数N线性增长:Di=ni/Ni;
疲劳破坏判定为:D=1
若在k个应力水平Si作用下,各经受ni次循环,则其总损伤可定义[3]为:
(9)
则线性累积损伤理论的破坏准则[3]为:
(10)
式中:ni是在Si作用下的循环次数,由载荷谱给出;Ni是在Si作用下循环到破坏的寿命,由S-N曲线确定。
Miner累积损伤理论是线性的,损伤和载荷Si、载荷的作用次序以及D无关[3]。叶轮低周疲劳分析的重要理论基础,计算分析通过一段载荷对叶轮造成的损伤,计算出当累计损伤达到破坏准则时经历的循环数,当循环数对应的公里数大于客户目标时认为该叶轮的低周疲劳风险较低,反之较高。
5 叶轮低周疲劳计算分析
叶轮低周疲劳分析以压气机叶轮离心应力分析为基础,压气机叶轮的离心应力与转速的关系为二次方关系,当计算得到一定转速下叶轮的应力后可以很方便地计算出在不同转速下,压气机叶轮的应力分布。
在计算叶轮的疲劳寿命之前需要通过计算该叶轮在最大载荷下的应力,排除叶轮强度失效的风险,并确定最低寿命位置[4]。
叶轮材料2618,密度ρ=2.66×103kg/s,弹性模量E=6.9×104MPa,泊松比0.31。根据客户提供的载荷压气机最高运行转速213 400 r/min。
叶轮的高速旋转给整个叶轮带来较大的应力,分布如图6所示。

图6 压气机叶轮应力分布
在最高转速下,应力最大的位置为压气机叶片的叶根位置和轴孔位置,分别为257 MPa和242 MPa,最大应力没有超过材料的极限应力,所以该叶轮没有强度破坏风险。参考不同温度下的S-N曲线,温度越高在相同应力下低周疲劳风险越高,压气机叶轮的正常工作过程中,叶片由于直接接触气体所以温度较高,综合考虑得到,该叶轮低周疲劳的风险位置为压气机叶轮出口倒角位置。如果压气机叶轮应力最大位置与温度最高位置不统一,需要根据等损伤理论对不同位置的载荷进行损伤分析,以确定低周疲劳的风险位置。
加载简化后的循环曲线作为载荷输入,根据估算的S-N曲线,采用Goodman载荷转换方式,根据Miner累计疲劳破坏理论,寿命D=λ∑ni/Ni预估该叶轮寿命如图7所示。

图7 叶轮叶根位置寿命图
计算在该载荷下,叶轮的最大循环次数为1 130次;
叶轮寿命对应的公里数为L=200 km×1 130=225 080 km≥200 000 km,满足客户要求。
6 结论
文中运用ANSYS软件的低周疲劳分析模块,总结了叶轮低周疲劳所需要的理论知识,建立了一种较为方便使用的增压器叶轮的低周疲劳分析流程,并通过该流程对发动机用增压器的压气机叶轮进行了低周疲劳风险分析,排除了该压气机的低周疲劳风险。
