技术创新与城市经济增长波动——基于我国15个副省级城市面板数据的实证研究

冯云廷 计利群（东北财经大学经济学院，大连 605） （东北财经大学经济与社会发展研究院，大连 605）

引 言

我国自加入世界贸易组织后，经济增长经历了飞速发展的10年。根据国家统计局发布的信息，2003～2011年，中国经济年均实际增长10.7%，社会生产力和综合国力显著提升。2012年以来，我国经济发展增速主动放缓并逐渐步入 “新常态”，从高速增长阶段向高质量发展阶段转变。政府致力于调整和优化经济结构，加快转变经济发展方式，实施创新驱动发展战略。党的十八大报告指出：“科技创新是提高社会生产力和综合国力的战略支撑，必须摆在国家发展全局的核心位置。”党的十九大报告进一步指出：“创新是引领发展的第一动力，是建设现代化经济体系的战略支撑。”技术创新对经济发展的推动作用日益明显。

城市作为我国经济的重要载体，是带动整个国家经济发展的主要力量。伴随着城市化进程的深入，我国大部分城市同样经历了经济的高速增长到中高速发展的转变。尽管我国城市经济总体上呈现大致相同的变化趋势，然而不同城市的经济增速波动的幅度却有很大的差异。如沈阳市2007年全市地区生产总值增速达20.4%，而2015年则降低到3.2%；武汉市2007年全市地区生产总值增速为15.6%，到2015年则是8.8%。计算2000～2017年这两座副省级城市全市地区生产总值增速的变异系数来衡量经济增速的波动程度，沈阳市约为0.55，武汉市约为0.18，两者差异明显。同时，两座城市的另一组对比数据同样引人思考。根据国家知识产权局发布的专利统计年报，2000年沈阳市的年度专利授权量为1949件，比同年份武汉市的1038件多出911件；而2017年沈阳市的年度专利授权量为9891件，比同年份武汉市的25528件少15637件。

以往，城市经济增长往往依靠传统生产要素投入数量的增加，但这种推动经济增长的方式总会遇到瓶颈，产生如资源配置不合理、产能过剩和资源利用效率低下等负面影响。当前，我国许多城市的经济增长面临着新旧动能转换，要加快通过技术创新推动经济增长的发展任务。探讨技术创新与我国城市经济增长波动之间的联系，并分析其内在机制有较强的现实意义。

1 文献综述

众所周知，技术创新能够有效促进经济增长，但关于技术创新对经济波动的影响，不同的研究往往有不同的结论。现有关于技术创新、技术进步或技术冲击对经济波动影响的研究可以归纳为以下几方面：

（1）从内容角度看，此类文献以讨论经济周期相关问题最为常见，而且观点和结论不尽相同。实际经济周期理论认为技术冲击是经济周期波动的重要冲击源。 Kydland和 Prescott［1］发现， 实际经济周期模型可以解释美国经济波动的77%，技术冲击成为主要的波动动力来源。陈师等［2］将偏向性技术变迁和投资专有技术变迁引入到实际经济周期 （RBC）模型，测算该模型能够解释85%和94%以上的中国经济波动特征。丁任重等［3］的分析表明技术创新冲击对我国经济周期的影响具有十分显著的正向效应，技术创新在繁荣阶段与经济周期运行的关联度要高于衰退阶段。虽然普遍承认技术冲击是经济波动的重要冲击源，但仍有部分学者对技术冲击能够解释大部分的经济波动持怀疑态度。Galí等［4］的研究从技术冲击和总体经济波动角度测算了实际经济周期模型与美国战后经济数据的吻合程度，结果是 “吻合程度不太好”，总体技术冲击的作用是有限的。新凯恩斯主义的动态随机一般均衡 （DSGE）模型，则更加强调需求冲击的作用，而不是技术的作用。徐舒等［5］在动态随机一般均衡模型 （DSGE）的理论框架下建立的内生R＆D投入与技术转化模型较好地解释了我国1989～2008年的现实数据83.3%的经济波动；（2）从研究对象角度，此类研究主要以国家的宏观经济为研究对象，以城市经济为研究对象的相对较少。如袁秀明［6］、陈漓高等［7］分别以美国为研究对象，分析了技术冲击、技术进步与美国的经济波动关系；陈乐一等［8］采用我国30个省、市、自治区数据研究了要素偏向型技术进步对我国经济波动的影响。相对而言，对我国城市技术创新与城市经济波动的研究往往以特定类型城市为对象，如陈妍等［9］以东北地区资源型城市为对象进行研究，认为经济周期性波动与国家振兴老工业基地政策和城市产业结构调整历程相吻合，技术进步对经济增长贡献较小； （3）从变量选择角度，尽管收入、贸易、就业等数据也可以度量经济波动，但更多的研究选择国内生产总值 （GDP）总量或人均国内生产总值 （人均GDP）的变化，或二者的同比增速变化为代理变量；技术创新或技术进步多选择专利或研发投入相关变量作为代理变量。得到变量波动成分的处理方法主要包括标准差法、HP滤波方法和一阶差分等方法，其中以HP滤波方法较为常见。如方福前等［10］、 陈太明［11］、 欧阳秋珍等［12］的研究均涉及了以上内容与方法。

综上所述，技术创新对经济波动的影响因研究对象不同而有显著差异，现有的研究一般比较宏观，普遍缺少对城市经济波动的研究。我国城市经济增长正处在由要素驱动向创新驱动转变的关键期。本文基于我国一些城市经济增长率大幅波动及专利数据变化的一些事实，在参照现有文献的基础上，探讨城市技术创新对城市经济增长波动的影响及其内在过程。

2 理论依据与假说

近20年我国城市的经济高速增长是伴随着快速的城市化进程共同发生的，突出地表现在地区生产总值的增长、城市人口的集聚、城市空间的扩展、基础设施的改善和生产技术的提升。因此，资本、劳动力、土地和技术在城市经济增长中都在发挥着作用。关于技术在经济增长中的作用，新古典增长理论的索洛模型将 “技术进步”作为外生变量而不必解释。内生增长理论则把技术变革作为市场活动的结果，而不是无法解释的外生变量。内生增长理论中的熊彼特增长模型提出了一个简单却重要的观点：在长期中，经济的平均增长率等于创新的频率乘以创新的规模［13］。这深刻阐述了创新活动与经济增长之间的关系。熊彼特增长理论是由当代著名的经济学家菲利普·阿吉翁（PhilippeAghion） 和彼得·豪伊特 （Peter Howitt）创立发展的。他们最突出的贡献是建立了基于 “创造性破坏”的阿吉翁-豪伊特 （Aghion-Howitt）模型，并将其发展成为一个统一的分析框架，从而把熊彼特经济增长理论带回到主流宏观经济理论中。由于阿吉翁-豪伊特型的理论思想来自于熊彼特的 “创造性破坏”，所以阿吉翁-豪伊特模型通常被称为熊彼特增长模型［14］。如果认为不同城市具有不同的创新频率和创新规模，那么不同城市的长期平均经济增长率是不同的。

同时，实际经济周期理论认为技术冲击是经济波动的重要来源。实际经济周期模型认为类似于石油危机、农业歉收、战争、技术革新等实际冲击导致了经济的周期波动，其中技术冲击是导致经济周期波动的最常见和值得分析的冲击［15］。实际经济周期理论忽略了货币变动在推动宏观经济波动中的作用，认为经济活动中的波动仅来自长期总供给的冲击。与实际经济周期理论观点不同，新凯恩斯主义经济学家观点更加强调需求冲击。他们考虑到经济行为主体对货币因素扰动可以做出跨期理性决策，使得短期总供给和总需求曲线的移动更加符合现实社会经济，构建了动态随机一般均衡 （DSGE）模型。鉴于此，将技术创新作为城市经济增长波动的重要来源是符合实际经济周期理论的，但同时也不能忽略供给和需求两方面的其他因素。

从熊彼特增长理论的角度，城市的创新活动决定了城市的长期平均增长率。经济周期理论启示供给因素和需求因素都是城市经济增长波动的重要波动源，其中技术冲击尤其值得重视。以往生产要素数量的投入在我国城市经济增长中起到重要的拉动作用，同时也伴随着经济增长的明显波动。技术创新是重要的创新活动，影响着城市长期的经济平均增长率。在我国现阶段，如果技术创新在经济增长中起到稳定的拉动作用，必然可以抵消部分要素投入变化带来的经济波动。结合我国城市处于 “三期叠加”现实背景，本文认为：“在其他条件相近的情况下，城市技术创新波动与其经济增长波动具有此消彼长的关系。”换一种说法：“在其他条件相近的情况下，城市的技术创新对经济增长波动具有熨平效应。”如果假说成立，其内在过程具有严谨的逻辑性。本文尝试以我国15个副省级城市为样本对假说进行检验。

3 模型设定、数据来源和变量

3.1 模型设定

鉴于本文实证所选择的研究对象是城市，而城市个体之间的特征差别很大，但单个城市的特征随时间的变化相对缓慢，所以直接设定如下个体固定效应变截距面板数据模型：

其中，被解释变量Vgrowthi，t表示城市经济增长波动，核心解释变量Vinnovationi，t表示技术创新变化的波动，Zi，t表示其他控制变量，c表示常数项，μi表示个体固定效应；β和θ表示各回归变量的系数， εi，t表示残差项。

我国幅员辽阔，地区差异因素往往不容忽视，而技术创新行为往往与地区的创新精神、创新环境等因素相关。为了在控制城市所在区域因素的基础上进一步考察核心解释变量对被解释变量的影响，本文利用虚拟变量建立了变系数面板数据模型。按照常规将我国主要区域划分为东北地区、东部地区、中部地区、西部地区。其中哈尔滨、长春、沈阳、大连属于东北地区；济南、青岛、南京、杭州、宁波、厦门、广州、深圳属于东部地区；武汉属于中部地区；成都和西安属于西部地区。设置3个虚拟变量如下：

D1i＝D2i＝D3i＝0表示城市位于西部地区。建立变系数面板数据模型如下：

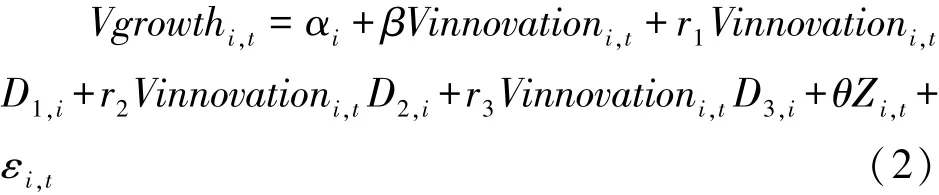
3.2 样本、变量选择及数据来源

3.2.1 样本选择和数据来源

基于数据的可得性和统计口径的一致性，本文选取15个副省级城市作为研究对象。这些城市技术创新活动活跃、经济体量相当、地域分布广泛，覆盖了我国东北、东部、中部和西部地区，具有广泛的代表性。主要数据来自2001～2017年《中国城市统计年鉴》和2000～2017年国家知识产权局 《专利统计年报》，部分数据参考各城市统计年鉴。

3.2.2 代理变量的选择

一般意义上讲，波动可以理解为实际对长期趋势或潜在水平的短期偏离。经济波动通常采用GDP或人均GDP的波动来度量，而经济增长通常采用GDP或人均GDP的实际增长率表示。本文要考察的城市经济增长波动选取城市市辖区范围内地区生产总值的增长率的波动来表示。核心解释变量采用文献中通用的专利数据变量来代替，本文选取城市年度专利申请授权量的波动来表示技术创新的波动。尽管专利申请授权量指标不能完全反映技术是否转化为推动经济增长的现实生产力，但该指标是城市技术创新能力的重要表征。专利申请授权量大的城市，拥有更多可以转化的资源，因而经济增长从中受益。

在核心解释变量的基础上，本文还从供给和需求角度引入了一些其他控制变量以控制其他主要因素对城市经济增长波动及其内在过程的影响。本文在控制变量的选取和处理方面参考吴建銮的做法［16］，具体包括：（1）投资因素。投资是影响我国经济增长最活跃的因素之一。尤其是在经济增长乏力时，投资是稳定经济增长和就业的有效抓手。本文选择固定资产投资变动作为投资因素对经济增长波动影响的代理变量；（2）消费因素。居民消费水平变动是影响经济增长波动的基础因素，这里选择社会消费品零售总额变动代表消费因素对经济增长波动的影响；（3）贸易因素。选择城市进出口总额的变动作为贸易因素对经济增长波动影响的代理变量；（4）劳动力因素。劳动力供给是经济生产活动的基础要素，这里选择城市城镇就业人员数、私营企业和个体劳动者数量的和的变动作为劳动力供给冲击对经济增长波动的影响代理变量；（5）价格因素。物价水平影响居民的实际消费购买能力，不仅与居民收入、消费偏好、商品产量等因素相关，而且受到货币政策的直接影响。本文选择消费者物价指数的变动作为价格因素影响经济增长波动的代理变量。

3.2.3 数据的处理

衡量经济波动的方法有滚动标准差、HP滤波、BP滤波等。HP滤波法可以较好地分解出时间序列的趋势要素，具有简便、灵活、模拟效果好等优点，本文选择用HP滤波法对技术创新和经济增长的波动进行测算。HP滤波法是由Hodrick和Prescott于1980年在分析美国战后的经济景气时提出的，之后被广泛应用于对宏观经济趋势的分析研究。该方法认为Y＝G＋C，其中Y是经济时间序列， Y＝｛y1，y2，…，yn｝， G 是趋势要素成分的时间序列， 为 G＝｛g1，g2，…，gn｝， C 是波动要素成分的时间序列， 为 C＝｛c1，c2，…，cn｝， n 为样本容量。可以将yt分解成为：yt＝gt＋ct。时间序列Y中趋势要素G被定义为如下式 （1）的最小化问题的解：

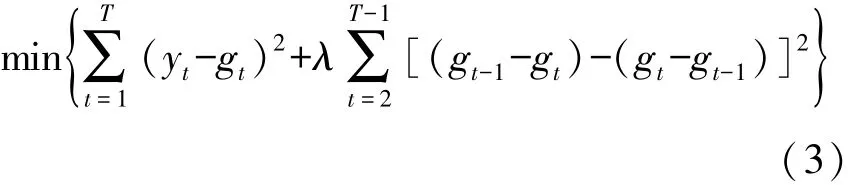
HP滤波依赖参数λ，并随着λ的增大而增大。根据一般的经验，当使用年度数据时λ＝100。

图1 HP滤波法的2000～2017年我国GDP增速及15个副省级城市GRP增速的波动部分

图1是对2000～2017年我国国内生产总值（GDP）增长率和15个副省级城市地区生产总值（GRP）增长率采用HP滤波方法分解出的波动成分。图片由Eviews10生成。对比发现，期间不同城市的经济增长率波动成分图形不仅与全国经济增长率波动图形不十分吻合，而且各自的差异十分明显。

表1列出了模型中所有变量的符号和数据的具体处理方法，变量的统计性能描述见表2。

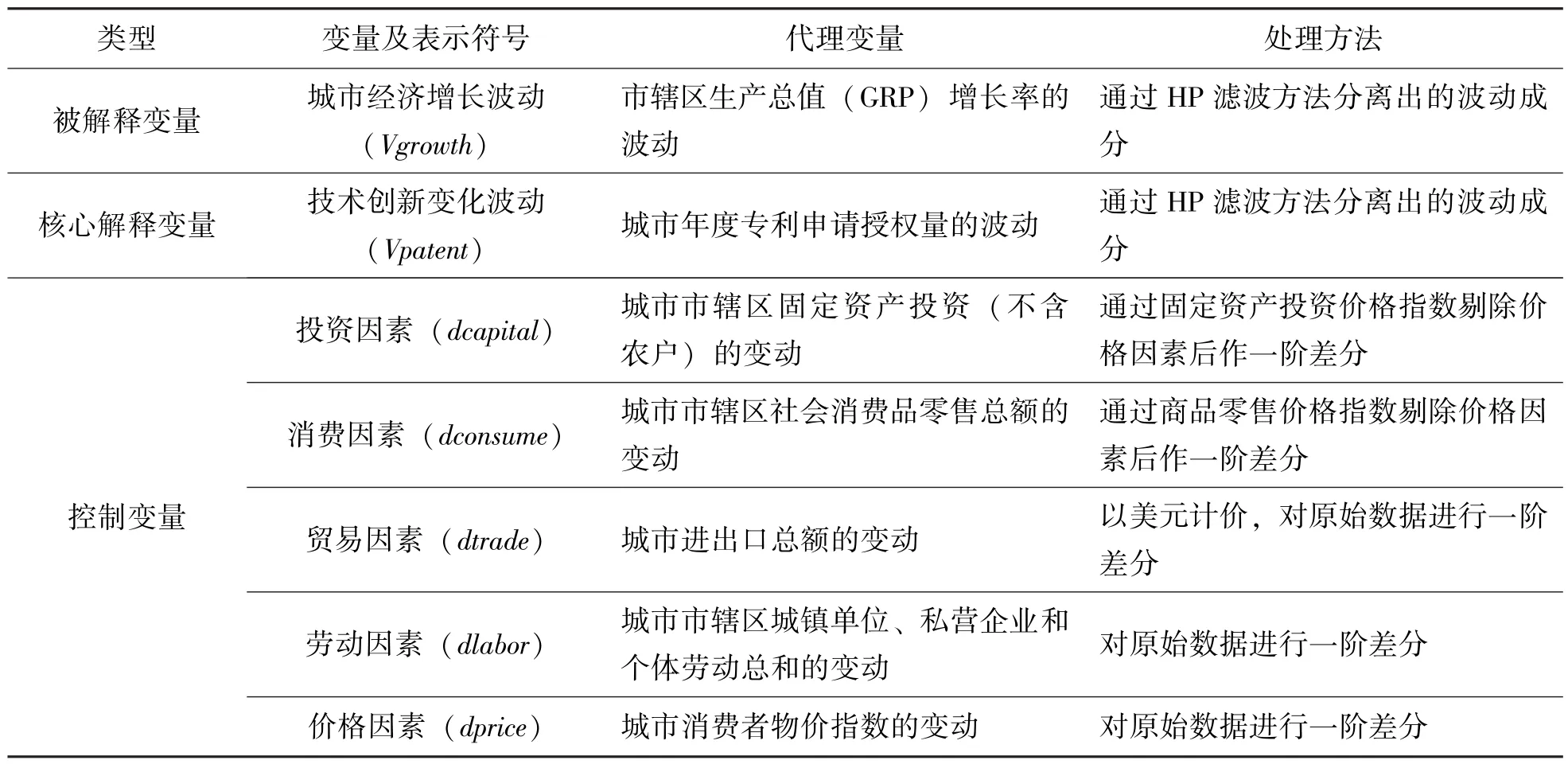
表1 变量指标的选择与处理

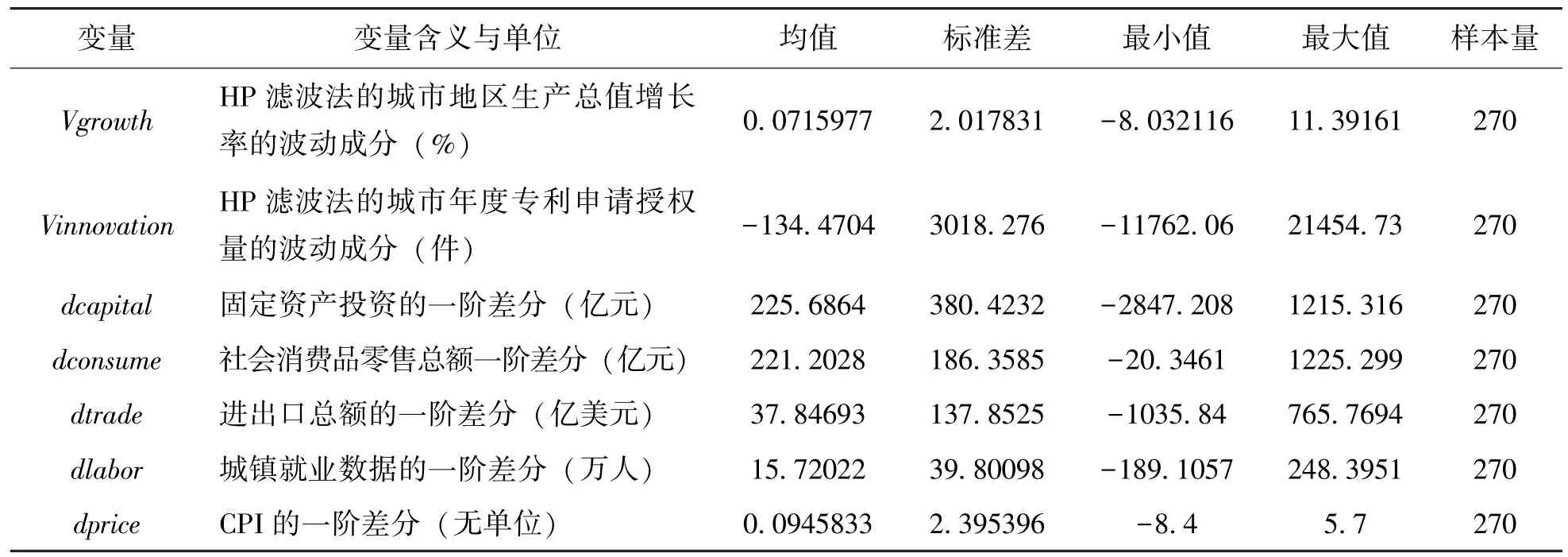
表2 变量的统计性描述

4 实证分析

基于前文设定的模型，本文从实证的角度考察技术创新变化的波动对城市经济增长波动的影响及分析其内在过程，并对模型进行稳健性检验来评价结论的可靠性。所有的估计结果通过Stata14.0得出。

4.1 单位根检验

为了减少伪回归，在进行实证之前应该对变量进行单位根检验。常见的单位根检验方法有LLC、IPS、 Breitung、 Fisher-ADF、 Fisher-PP、 Hadri LM检验等，为了避免单一检验方法造成的偏误，本文选择 LLC［17］和 IPS［18］两种方法进行单位根检验。检验结果如表3所示。根据检验结果，我们认为本文的数据是平稳的。

4.2 实证结果与分析

4.2.1 个体固定效应变截距面板数据模型的估计基于不同城市在技术创新理念、技术创新政策、技术创新能力等方面存在着个体差异，而单个城市个体的这些特性随时间变化相对比较缓慢的基本分析，本文认为建立个体固定效应模型较为妥当。同时，F检验表明面板数据的个体效应明显，建立面板数据混合模型是不合适的。按照统计理论，应该进一步对模型的固定效应或随机效应进行统计学检验，常用的检验方法是Hausman检验。但鉴于样本数量等方面的原因，本文没有进行相关检验，而是在个体固定效应回归基础上同时进行个体随机效应的回归估计，以此来进行对比并作为模型稳健性检验的一部分。在回归方法上，个体固定效应模型采用组内 （Within）估计方法，个体随机效应采用可行广义最小二乘法（FGLS）。为了更好地显示控制变量的引入过程及对解释变量回归结果的影响过程，本文采用逐渐添加控制变量的方法对回归结果进行展示。模型1～5为个体固定效应模型在控制并逐渐添加投资、消费、贸易、劳动和价格因素情况下考察核心解释变量对被解释变量的影响；模型6是个体随机效应模型的结果，用来与模型5进行对比并作为稳健性检验的一部分。模型1～5采用组内估计方法，模型6采用可行广义最小二乘估计方法。

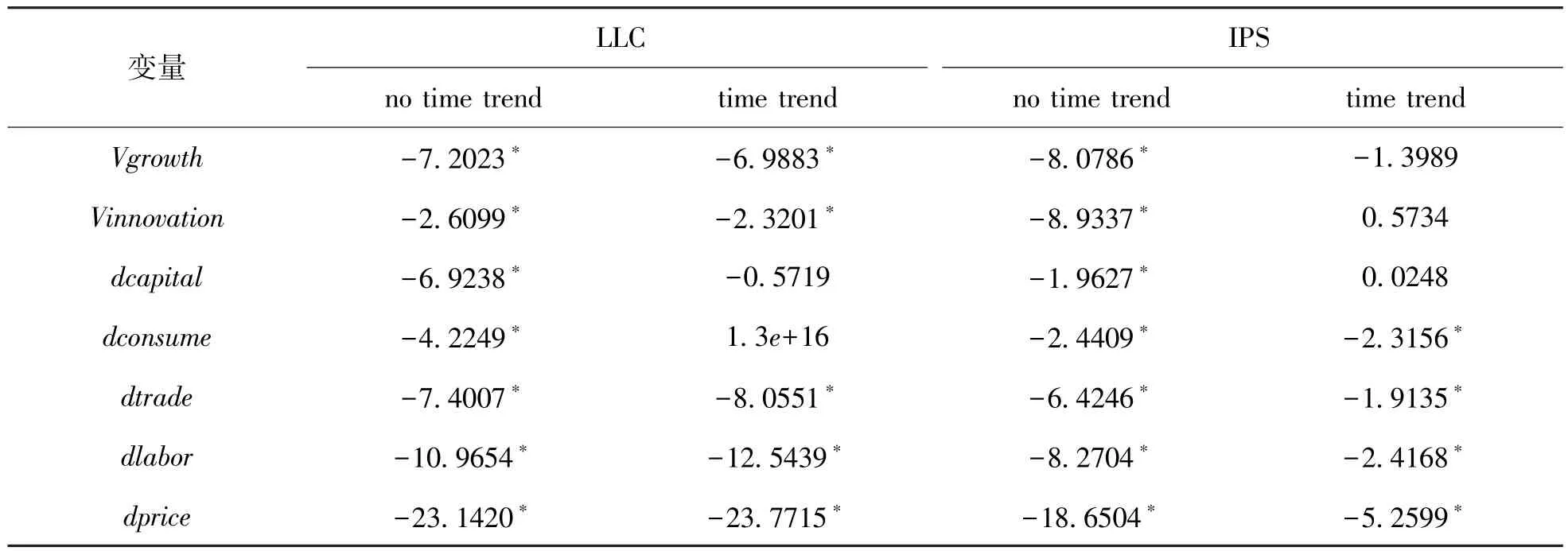
表3 变量单位根检验

从表4结果可以看出，个体固定效应模型1～4中核心解释变量对被解释变量的影响通过了1%的显著性检验，模型5则显示其通过5%的显著性检验。同时系数符号均为负值，说明技术创新变化的波动与城市经济增长波动之间存在着稳定的负向关系。从模型系数上看，模型5核心解释变量系数的直接含义表示15座副省级城市在2001～2017年间，在控制投资、消费、贸易、劳动和价格因素变量不变情况下，专利申请授权量波动每增加10000，城市经济增长率波动平均减少0.67%，对经济增长波动具有熨平效应。

从控制变量上看，模型5显示投资因素的波动和价格因素的波动对城市经济增长波动的影响通过1%显著性检验，并且是正向的。贸易因素的波动对城市经济增长波动的影响通过10%显著性检验，同样是正向的。消费因素和劳动因素的波动对城市经济增长波动的影响未能通过显著性检验，同时消费因素波动对应的系数是负的。这些与我国经济的实际情况基本是相符的。众所周知，投资、消费和净出口一直被认为是拉动城市经济增长的 “三驾马车”，其中投资和出口也是经济宏观调控政策重要的着眼点，两者本身的波动对经济增长波动的影响较为直接。我国国内消费市场稳健发展，是带动经济增长的重要稳定力量，其潜力十分巨大，城市消费波动程度也相对较小。我国城市就业市场一直是稳字当头，劳动因素的波动对经济增长波动影响不显著；而价格因素的波动对经济增长波动的影响是十分显著的。

个体随机效应模型6是个体固定效应模型的对照模型，其结果与模型5的结果基本一致，这也一定程度检验了模型5的稳健性。

4.2.2 控制地区因素的变系数模型的估计

我国幅员辽阔，地区之间存在着自然地理、社会环境、经济结构及人们思想观念等多方面的差别。技术创新的地区差异因素不仅会影响模型的截距项，也可能会影响模型的结构，因此假设样本城市所在地区能够影响模型系数，利用理论设定模型 （2）式在控制地区因素的基础上进行回归分析。在统计检验上，LR检验表明建立混合模型是不合适的。同时基于上文分析，这里设定计量模型截距项为个体固定效应，考察核心解释变量在控制样本城市所在地区的情况下对被解释变量的影响。检验结果显示 （表略），除西部地区外，在控制东北、东部、中部地区情况下，核心解释变量对被解释变量的影响均通过了1%的显著性检验，符号也均为负。控制变量的显著性和符号与个体固定效应变截距面板数据模型的估计结果的显著性和符号相同，系数数值相近。考虑到我国大部分城市集中在中东部地区，基本可以认为在控制地区因素的情况下，核心解释变量对解释变量的影响是显著的。从系数数值上看，技术创新对稳定东北地区经济波动的作用更加明显。

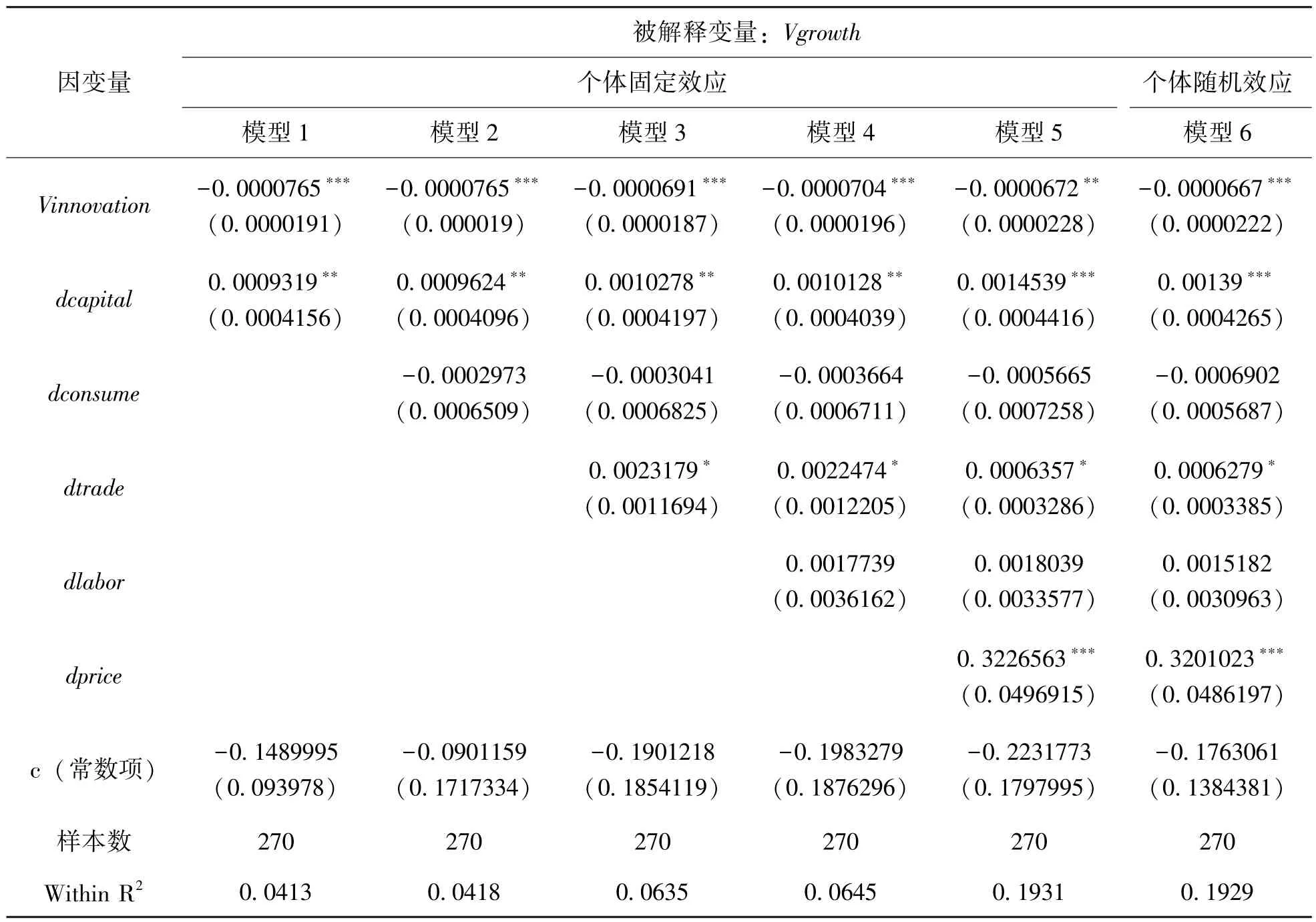
表4 个体固定效应变截距模型的估计结果

4.3 稳健性检验

为了检验结论的稳健性，这里采用替代被解释变量、对数据进行分类回归和分时间段回归的方法进行检验。这里选用人均地区生产总值 （人均GRP）增长率的波动替代被解释变量进行检验。尽管地区生产总值和人均地区生产总值二者有内在的联系，但人均地区生产总值更能反映一座城市的综合发达程度。分类回归是指采用以秦岭淮河为南北分界线将样本城市分为南方城市和北方城市进行的回归检验。南方城市包括南京、杭州、宁波、厦门、广州、深圳、武汉、成都；北方城市包括西安、济南、青岛、大连、沈阳、长春、哈尔滨。分段回归是指将数据的年份时间段分成2000～2009年和2010～2017年两个时间段分别进行回归检验。以上检验在个体固定效应模型下进行，其主要结果显示 （表略），核心解释变量均在10%显著水平上显著，基本验证了上文模型结论的稳健性。

4.4 实证结果的进一步探讨

4.4.1 技术创新对经济增长波动具有熨平效应符合我国事实

实证结果表明2000～2017年我国15个副省级城市技术创新并没有加剧经济增长的波动，相反对经济增长波动具有一定的熨平效应。这似乎与实际经济周期理论中技术冲击是经济波动的重要来源观点不一致，但本文并不认为这是矛盾的。本文实证是在我国经济由高速增长向高质量增长转型背景这个定位基础上的时间跨度较短的实证分析，无法替代长期的分析。同时，从我国经济波动来源的识别方面看，现有的一些重要研究成果表明投资、土地财政等因素［19，20］，而非技术冲击因素是我国经济波动的主要因素，这对理解本文中技术创新对城市经济增长波动具有一定的熨平效应有很大帮助。

关于经济增长阶段，有观点认为初期的经济增长是由资本积累驱动的，而资本积累为知识的逐渐增长创造条件而不必受制于土地的递减报酬；此后，创新将越来越发挥作用［21］。技术创新能够长期推动经济增长，作用的稳定性强于要素扩张。技术创新在对我国城市经济增长的促进作用逐渐增强时，对城市经济增长波动具有熨平效应是符合我国城市经济增长波动的事实的。

4.4.2 熨平效应的逻辑分析

为了更好地阐述和理解这种熨平效应的作用机制，本文需要在我国城市经济处于转型期这个前提下结合作者已有的研究成果加以说明。冯云廷等［22］从城市创新能力与城市经济结构变化之间的内在关系角度探讨了城市兴衰的原因，认为城市创新能力是内生于经济结构的，经济结构的转换同方向地影响着城市创新能力；经济结构本质上是资源配置结构和利益分享结构，是各类决策主体行为选择的结果，而结构调整和优化是微观主体再选择的过程；产业多样性或产业链网络完备的、多元的、开放的经济结构往往可以转换成更强的城市创新能力；城市经济结构转换对创新能力的作用程度决定了城市兴衰。由此可见，城市的技术创新同样是内生于城市经济结构的，城市技术创新成果较大的提升是市场机制下城市经济结构转换的反映，是在市场机制中行为主体主动的、自发的行为选择的结果。这种各类行为主体经过市场机制筛选后的、能够自我负责的、主动自发的行为能够形成持久稳定的经济增长推动力，抵消部分非市场因素和外部环境变化的作用，从而对经济增长的波动具有熨平效应。经济转型重要特征就是发挥市场配置资源的能力，弱化非市场因素的影响。因而，技术创新对城市经济增长波动的熨平效应就符合逻辑。

5 结论与政策启示

本文基于我国15个副省级城市2000～2017年的面板数据构建变截距面板数据模型和控制地区因素的变系数面板数据模型，实证了技术创新对城市经济增长波动的影响，进而讨论了这种影响产生的内在过程及其机制。实证计量模型结果表明：在控制其他条件情况下，城市技术创新 （以专利申请授权量表示）的波动与城市经济增长率的波动之间存在着稳定的负向关系，在控制地区因素时，结论基本成立；从实证数据上看，总体上城市专利申请授权量每增加10000，城市经济增长率波动平均减少0.67%。本文认为实证结果证实了城市技术创新对我国城市经济增长波动具有熨平效应的假说。结合作者已有的研究成果发现，技术创新的熨平效应通过市场机制发挥作用，抵消或弱化非市场因素的影响。城市技术创新内生于城市经济结构，是行为主体自主与自发的行为结果，通过了市场的筛选作用，具备稳定的经济增长推动力。

通过研究结论可知，城市获得稳定经济增长的重要路径是促进技术的持续创新，技术持续创新的城市拥有更加稳定的经济增长率。多元的、开放的经济结构往往可以转换成更高的城市创新能力，因此调整优化经济结构是获得创新能力的有效途径。为此应减少短期经济刺激手段，着眼于提升城市技术创新能力。因此打破单一的、封闭的经济结构，培育形成多元的、开放的经济结构是长久之计。