GB/T 228.1—2010应变速率应用情况及对新版标准的建议

2020-12-25徐惟诚田慧玲

理化检验(物理分册) 2020年12期

方昊, 徐惟诚, 田慧玲

(宝山钢铁股份有限公司制造管理部, 上海 200941)

2009年发布的ISO 6892-1:2009MetallicMaterials—TensileTesting—Part1:MethodofTestatRoomTemperature，新增了基于应变速率控制的试验速率，称为方法A。此外ISO 6892-1:2009还完全保留了上一版对试验速率的相关规定，即方法B。GB/T 228.1-2010《金属材料拉伸试验第1部分：室温试验方法》对试验速率的规定与ISO 6892-1:2009的基本一致，也将试验速率控制分为方法A和方法B。GB/T 228.1-2010的这一变化在业内引起了持续的讨论，讨论焦点主要集中在速率控制方式(应变、应力和横梁位移)、速率大小及速率对检验结果和效率等方面的影响。笔者结合目前正在进行的GB/T 228.1-2010修订工作，就方法A应用中遇到的问题(主要是不连续屈服试样，采用方法A的推荐速率时，试样平行长度内应变速率的相对误差超±20%的规定)进行探讨，希望对该次标准修订工作有所贡献。

1 应变速率应用中可能出现的问题

1.1 引伸计控制方式存在速率失控等风险

较早期的试验机，不具备应变速率控制能力或控制精度不高，引伸计控制方式存在速率失控等风险[1]。为此，采用应变速率控制前，需对试验机的能力进行评估。

1.2 应变速率相对误差难以满足标准

对于不连续屈服材料，测定下屈服强度ReL和屈服点延伸率Ae时，要求试样平行长度内应变速率的相对误差为目标值的±20%。由于屈服伸长变形是不均匀的[2]，采用恒定的横梁位移速率控制且应变速率较低时，试样平行长度内应变速率的相对误差难以满足±20%的规定。

2 屈服阶段试验速率验证

笔者对GB/T 228.1-2010的方法A进行验证。方法A有两种不同类型的应变速率控制模式，第一种是基于引伸计的反馈而得到应变速率；第二种是根据平行长度估计的应变速率，由恒定的横梁位移速率来实现。

验证试验的设备为近期引入的配有高刚度液压平推夹具和全自动引伸计的国际知名品牌拉伸试验机，数据采样频率设定为50 s-1。验证速率范围为屈服阶段的应变速率范围2和范围3。

2.1 连续屈服试样的验证

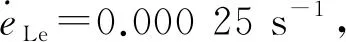
图1为连续屈服试样弹性及屈服阶段的应力-应变曲线，曲线呈典型的连续屈服特征。图2为屈服点及其附近应变速率及波动情况，可见屈服点及其附近引伸计标距内应变速率波动为0.000 1～0.000 4 s-1，即0.000 25 s-1相对误差±40%的范围内，超出相对误差±20%的要求，但符合ASTM E8/E8M-16aε1的控制方法B规定的应变速率及误差范围(0.015±0.006) mm·mm-1·min-1(即0.000 25 s-1，相对误差±40%)。仔细观察图2可发现，大部分时间点的应变速率在0.000 2～0.000 3 s-1，符合相对误差±20%的规定。

图1 连续屈服试样弹性及屈服阶段的应力-应变曲线Fig.1 Stress-strain curve of the continuous yield sample atelasticity and yield section

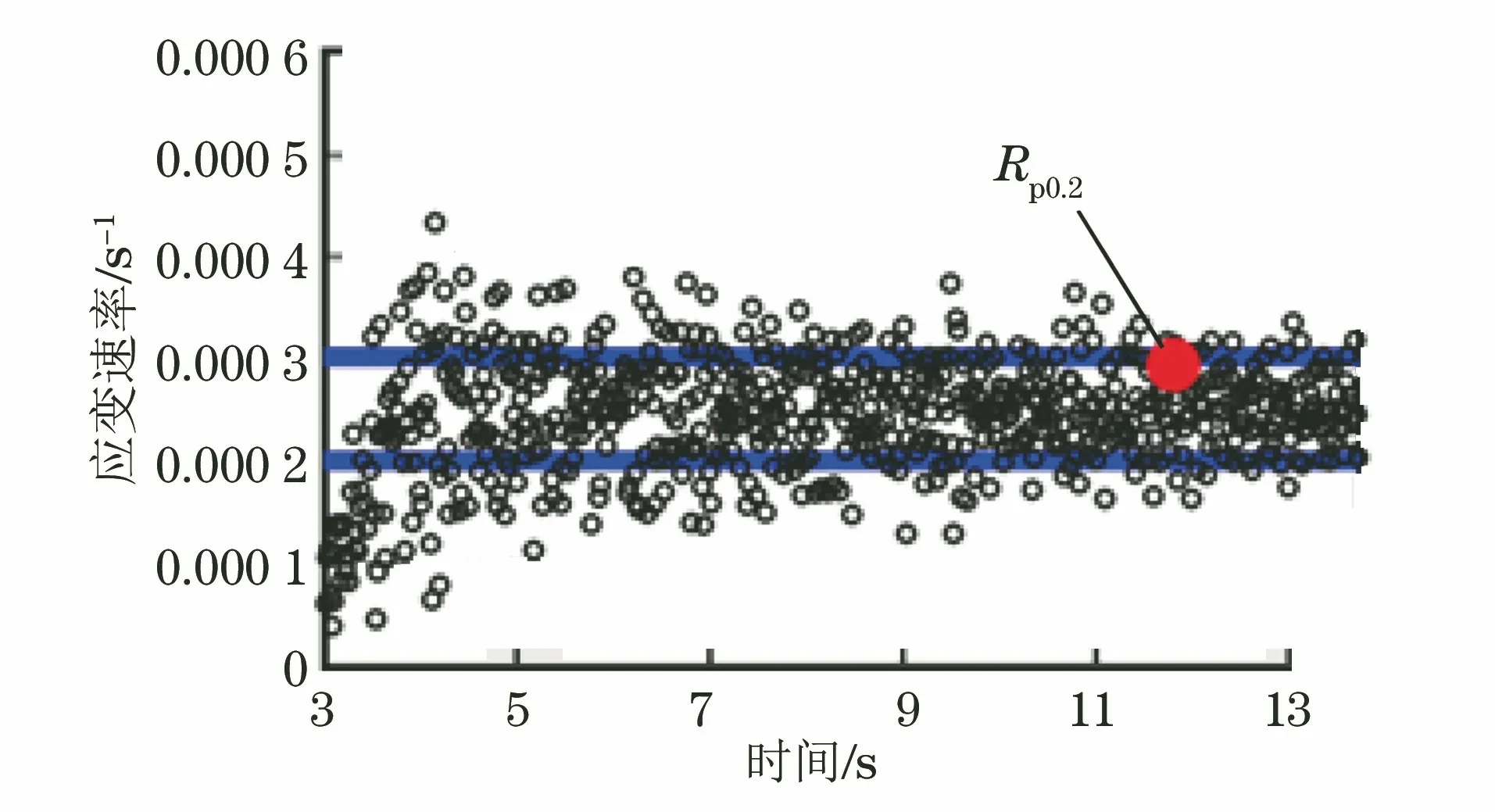
图2 连续屈服试样弹性及屈服阶段的应变速率-时间曲线Fig.2 Strain rate-time curve of the continuous yield sample atelasticity and yield section

2.2 不连续屈服试样的验证

2.2.1 验证速率范围2

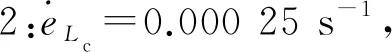
2.2.1.1 验证引伸计标距范围内的应变速率

验证试验采用GB/T 228.1-2010的P6带头试样，引伸计标距为80 mm。图3为不连续屈服P6试样弹性及屈服阶段的应力-应变曲线，曲线呈典型的不连续屈服特征。上、下屈服点及其附近应变速率及变化情况见图4，可见试样标距内的应变速率的相对误差约为±60%，超出了标准规定的±20%相对误差。

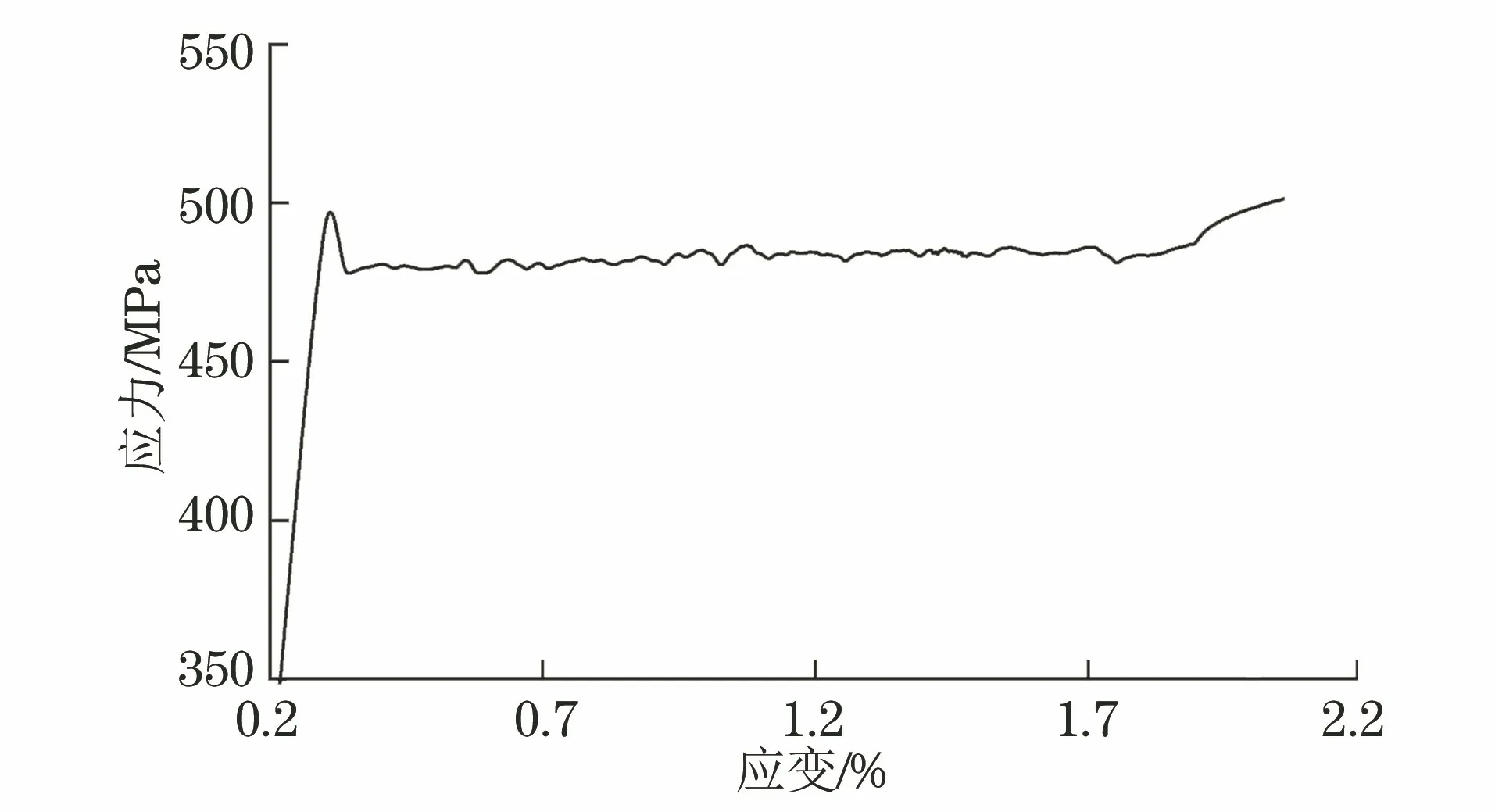
图3 采用速率范围2时不连续屈服P6试样弹性及屈服阶段的应力-应变曲线Fig.3 Stress-strain curve of the discontinuous yield sample P6 atelasticity and yield section in the rate range 2

图4 采用速率范围2时不连续屈服P6试样引伸计标距内弹性及屈服阶段的应变速率-时间曲线Fig.4 Strain rate-time curve in extensometer gauge length of thediscontinuous yield sample P6 at elastic and yield section in the rate range 2

2.2.1.2 验证平行长度范围内的应变速率

采用GB/T 228.1-2010的平行长度100 mm,宽度25 mm的P7带头试样。引伸计标距长度与平行长度约为100 mm。

GB/T 228.1-2010的3.5款：理想的L0应大于Lc/2但小于约0.9Lc,这将保证引伸计检测到发生在试样上的全部屈服(L0为原始标距,Lc为平行长度)。将引伸计标距长度设置为与平行长度相等，仅为了验证平行长度范围内的应变速率及速率相对误差能否满足标准规定。

图5为不连续屈服P7试样弹性及屈服阶段的应力-应变曲线，上、下屈服点及其附近应变速率及变化情况见图6，试样平行长度内应变速率波动主要集中在目标值的±60%，个别值达到目标值的±100%，超出了标准规定的±20%相对误差。

为排除速率波动系横梁位移速率不稳定所致，分析了横梁位移速率的波动情况。图7为图5对应试样试验时的横梁位移速率及其波动情况。由图7可见横梁位移速率非常稳定，波动范围仅为目标值的±0.8%。结合图2连续屈服试样应变速率的波动范围，可认为不连续屈服试样平行长度内应变速率波动主要由试样和测试系统引起。

图5 采用速率范围2时不连续屈服P7试样弹性及屈服阶段的应力-应变曲线Fig.5 Stress-strain curve of the discontinuous yield sample P7 atelasticity and yield section in the rate range 2

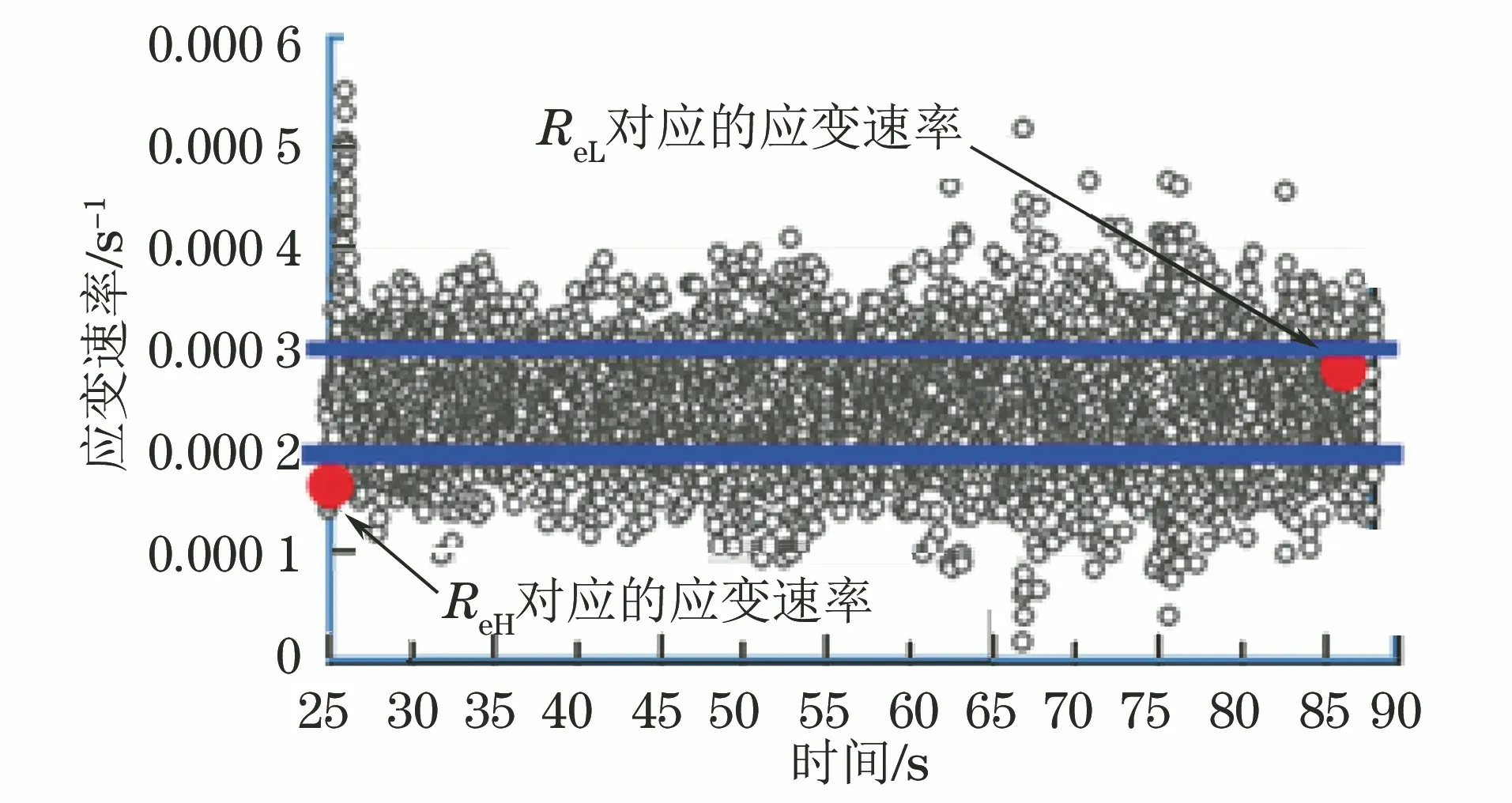
图6 采用速率范围2时不连续屈服P7试样平行长度内弹性及屈服阶段的应变速率-时间曲线Fig.6 Strain rate-time curve in parallel length of the discontinuousyield sample P7 at elastic and yield section in the rate range 2

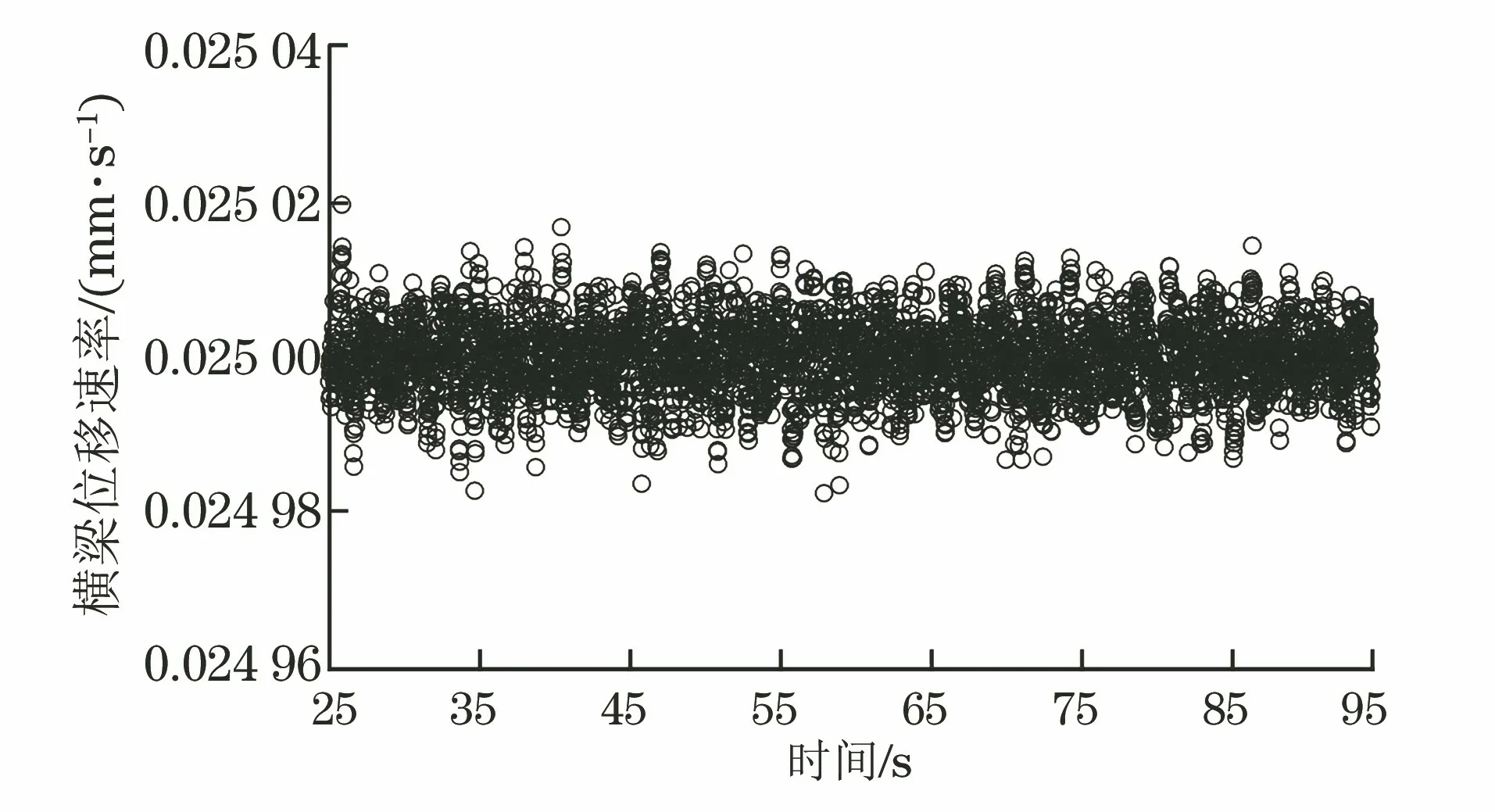
图7 采用速率范围2时不连续屈服P7试样弹性及屈服阶段的横梁位移速率-时间曲线Fig.7 Crosshead separation rate-time curve of the discontinuousyield sample P7 at elasticity and yield section in the rate range 2

2.2.2 验证速率范围3

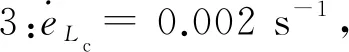
仅验证平行长度内应变速率的波动范围。采用GB/T 228.1-2010的平行长度100 mm,宽度25 mm的P7带头试样。引伸计标距长度与平行长度均为100 mm。

图8为不连续屈服P7试样平行长度内弹性及屈服阶段的应变速率-时间曲线，屈服点及其附近应变速率及变化情况见图9。可见，采用平行长度估计的应变速率范围3时，试样平行长度内的实际应变速率波动未超出标准规定的相对误差(±20%)。

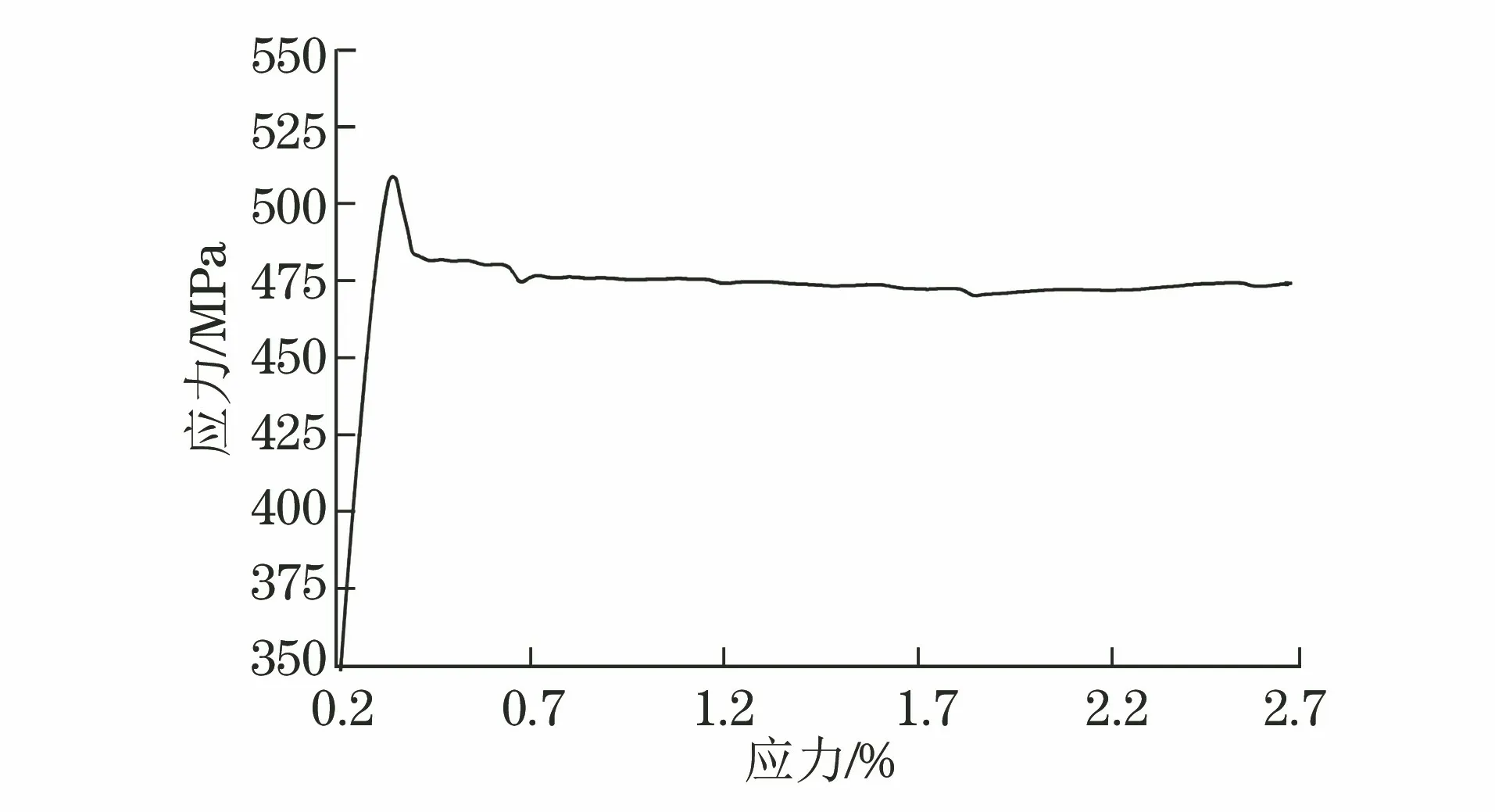
图8 采用速率范围3时不连续屈服P7试样弹性及屈服阶段的应力-应变曲线Fig.8 Stress-strain curve of the discontinuous yield sample P7at elasticity and yield section in the rate range 3

图9 采用速率范围3时不连续屈服P7试样平行长度内弹性及屈服阶段的应变速率-时间曲线Fig.9 Strain rate-time curve in parallel length of the discontinuousyield sample P7 at elastic and yield section in the rate range 3

3 分析与讨论

3.1 连续屈服试样

采用第一种应变速率的范围2(ISO 6892-1:2019的A1)时，由于试样标距内的应变速率是基于引伸计的反馈控制而得到的，应变速率波动主要来自试验机的机电仪系统。根据上述验证试验数据，现有试验机基本能将试样标距内的应变速率控制在±20%的相对误差内。如果适当扩大应变速率相对误差，比如将目前的±20%扩大至±40%，则能覆盖该次验证试验的应变速率波动范围。也与ASTM E8/E8M-16aε1的控制方法B规定的应变速率及误差范围(0.015±0.006) mm·mm-1·min-1(即0.0002 5 s-1±40%)相一致。

3.2 不连续屈服试样采用速率范围2

采用第二种应变速率的范围2时，屈服阶段(含上屈服附近)，试样标距内和平行长度内的应变速率波动均超出了±20%的相对误差。由于拉伸曲线的物理屈服点是材料特性和试验机系统共同作用的结果[2]，且试验系统达不到理想刚体，对于试样平行长度内屈服伸长为不均匀变形的材料，即使试验机能将横梁位移速率波动控制在极小的范围内，也无法将试样平行长度内的应变速率控制在某个恒定值或标准要求的±20%。GB/T 228.1-2010附录F给出的“考虑试验机刚度(或柔度)后估算的横梁位移速率”的方法，虽可将应变速率均值修正至目标值，但不能消除由试样不均匀变形引起的应变速率波动。文献[3]介绍了不连续屈服材料试样采用引伸计反馈的应变速率进行屈服阶段控制，屈服阶段应变速率在0.000 3 s-1左右，个别数据达到0.002 s-1。也表明不连续屈服试样采用速率范围2时，应变速率相对误差不满足标准规定。

根据该次验证试验，如果将第二种根据平行长度估计的应变速率的相对误差扩大至±100%，则能很好覆盖该次试验采用的试验系统的应变速率波动范围。

查阅ASTM E8/E8M-16aε1也能发现，其测定屈服特性的应变率控制方法，仅包含取自引伸计反馈信号的闭环控制，即GB/T 228.1-2010方法A中的第一种应变速率。

结合验证试验结果和ASTM E8/E8M-16aε1，对于GB/T 228.1-2010的第二种应变速率的范

围2，建议要么结合材料特性和目前主流的拉伸试验设备，适当扩大应变速率的相对误差，要么取消第二种应变速率。

3.3 不连续屈服试样采用速率范围3

不连续屈服试样采用第二种应变速率的范围3时，屈服阶段(含上屈服点附近)，试样标距内和平行长度内的应变速率波动均未超出±20%的相对误差。由于采用横梁位移控制时，试验机和试样夹持方式与范围2相同时，由试验系统造成速率波动是相近的，差异主要由试样引起。但应变速率由范围2的0.000 25 s-1提高到范围3的0.002 s-1时，同样为±20%的相对误差，范围3的速率波动幅度较范围2提高了8倍。