基于水平集函数的区间不确定性结构可靠性拓扑优化
2020-12-25陆小华李贵杰魏发远
陆小华,李贵杰,魏发远
(中国工程物理研究院总体工程研究所,四川 绵阳 621999)
1 引言
在传统的结构拓扑优化设计中,由于受到数学方法和计算速度等因素的限制,通常将输入参数视为确定的,进行确定性设计[1]。然而,实际工程问题中存在着大量的不确定性因素,如结构的几何尺寸、材料参数、初边值条件以及承受载荷等,这些不确定性会引起结构的性能波动,影响设计结果的可靠性。为此,文献[2]提出了结构可靠性拓扑优化设计(Reliability-based Topology Optimization,RBTO)的概念,将结构的材料参数、几何尺寸和载荷等参数视为不确定变量,并以可靠性作为拓扑优化的一个约束条件,将拓扑优化和可靠性优化设计结合起来,开展优化设计,使设计结果更加合理。
随着技术不断进步,可靠性拓扑优化设计的研究取得了丰硕成果。目前,考虑输入参数为随机变量的可靠性拓扑优化发展较为成熟。如:文献[3]使用可靠性指数法和性能评估法对随机不确定性结构进行可靠性分析,并用渐进结构优化方法完成拓扑优化,文献[4]对应力可靠性约束进行等价显式化处理,然后利用满应力准则法进行优化设计。为了提高优化效率,有学者提出了一次二阶矩方法[5],根据极限状态函数求出结构可靠度,并用来衡量结构的可靠性。但是,大多数的结构没有显示的极限状态函数,因此,文献[6]提出了标准响应面方法来构造极限状态函数,文献[7]提出用稀疏网格技术和随机响应面法来构造极限状态函数,然后再使用一次二阶矩方法进行结构可靠性分析。
计原理和裕度设计思想,能综合评价实际工程中结构的可靠性。为此,基于水平集函数,建立了以QMU 方法中位移置信因子为可靠性约束的结构可靠性拓扑优化模型。最后,使用移动渐近线算法(MMA)进行求解,通过悬臂梁算例验证了模型的可行性和使用方法的有效性。然而在实际工程中除了随机不确定性外,由于数据不足,还存在着大量的区间不确定性,针对输入参数为区间变量的可靠性拓扑优化问题,目前的研究较少,主要使用非概率可靠指标来评价结构的可靠性。如:文献[8]提出了非概率拟安全系数的概念,将非概率可靠性约束显式化处理,并使用水平集方法完成拓扑优化。文献[9]针对动态载荷作用下的区间不确定性问题,用结构非概率可靠性指标进行可靠性分析,并使用移动渐近线方法(MMA)求解。针对具有区间不确定性的热传导结构拓扑优化问题,文献[10]基于区间因子法推导出非概率可靠性指标,使用渐进结构优化方法进行拓扑优化。
上述方法几乎都是基于拉格朗日网格进行结构分析,拓扑优化的结果容易出现灰度单元、棋盘格式等网格变化所引起的数值问题。文献[11]中提出的基于水平集函数的拓扑优化方法,基于固定网格对结构进行分析,可以避免出现上述问题,而用水平集函数(Level Set Function,LSF)来描述结构,易于追踪结构边界的演变,并保证结构边界光滑。同时,文献[12]使用的裕量与不确定性量化(QMU)方法,结合了结构的物理设
2 基于水平集函数的拓扑优化方法
基于水平集函数的拓扑优化方法,首先借助自由设计区域建模器(Free-form Design Domain Modeler,FDDM)来定义结构的设计区域,借助拓扑变化建模器(Topology Variation Modeler,TVM)来实现一个规则区域的拓扑变化,然后通过两个建模器之间的R 函数运算,将拓扑变化限制在固定的结构区域内,使用固定网格对结构离散化,采用B 样条有限胞元法(BSFCM)进行结构分析,最后,使用MMA 算法对进行优化求解,实现拓扑优化设计。
2.1 自由设计区域建模器
自由设计区域建模器(FDDM)是一个描述优化结构具体形状的隐函数,它主要通过R 函数的运算将几个由水平集函数描述的结构组合,得到最终的结构。R 函数的定义如下[13]:

式中:φ1、φ2—描述两个结构的隐函数;∧、∨—R 函数中的R-合取和R-析取运算,运算规则和布尔运算中的布尔交∩和布尔并∪相同。
根据结构的具体形状,使用R 函数可构造出描述结构形状的水平集函数φFDDM(x)。
2.2 拓扑变化建模器
拓扑变化建模器(TVM)是通过插值函数构造而成的,规则区域内的拓扑变化可以通过插值系数的变化来实现。使用水平集函数来描述TVM,其定义为:

式中:ATVM—整个规则的TVM 区域;ΩTVM—在规则的TVM 区域内进行拓扑变化的结构区域;x—控制点坐标。
传统的水平集方法进行拓扑优化时计算复杂,效率较低。为此,使用径向基函数等插值函数构造参数化的LSF[11],通过对插值系数进行简单的参数优化即可实现LSF 描述的区域的拓扑优化。使用紧支径向基函数(CSRBF)构建TVM,其定义如下:

式中:φ(x)=(φ1(x),φ2(x),…,φN(x))T—由紧支径向基函数φi(x)组成的向量;p=(p1,p2,…,pN)T—由基函数的插值系数组成的向量,φ(x)只与选取的插值函数和控制点的坐标有关,因此水平集函数为参数化的形式。
2.3 拓扑优化模型
根据前面所构造的两种建模器,这里的拓扑优化方法由TVM 主导拓扑变化,通过FDDM 控制结构的真实设计域,通过R函数的运算将TVM 的变化“映射”到FDDM 上,实现FDDM 描述的真实结构的拓扑变化,其表达式如下:

式中:向量p—设计变量向量;φ(x,p)—的是此方法进行拓扑优化的真实结构区域Ω。
为了说明两个建模器的“组合”过程,以一个简单结构的初始拓扑模型的形成过程为例进行解释,如图1 所示。一个规则的拓扑变化区域,用来主导拓扑变化,如图1(a)所示。一个不规则的自由设计区域,如图1(b)所示。用来描述具体的优化结构,将二者进行布尔交运算,即可得到的拓扑优化模型,如图1(c)所示。

图1 拓扑优化模型的建立过程Fig.1 Modeling Progress of Topology Optimization
3 基于QMU 的可靠性评价方法
文献[14]是一种评价复杂系统安全性和可靠性的新方法,其基本思想是通过设计足够的裕量,来保证已知的失效模式不对系统的性能产生影响,从而确保结构安全可靠。QMU 方法有三个关键要素:性能阈值、性能裕量M、不确定性U,如图2 所示。其基本原理[12]是:根据性能裕量M 是否能够覆盖不确定性U 来判断系统性能是否可靠。即用性能裕量和不确定性的比值CF 来表征系统的可靠性:

CF 称为置信因子,(1)若CF>1,表明系统性能裕量M 大于不确定性U,系统性能可靠;(2)若CF=1,不能确定系统是否可靠,一般视为不可靠;(3)若CF<1,表明系统性能可能落到性能通道外,可能发生故障或失效。
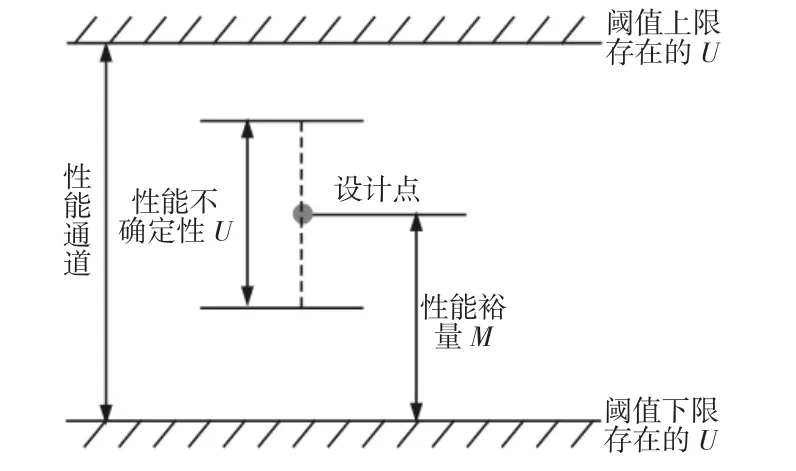
图2 QMU 基本原理示意图Fig.2 Diagram of QMU Principle
性能阈值根据结构的物理特性来确定,一般表示的是最坏的情况下的性能参数值,设最大节点位移dm为性能参数,给定许用最大节点位移为性能阈值,是一个确定值。由于弹性模量E和载荷F 具有不确定性,导致结构的位移也具有不确定性,根据E 和F 的不同边界值组合进行结构分析,计算出实际最大节点位移的取值范围为。根据QMU 方法的原理,性能裕量M 定义为结构实际性能值和结构性能阈值之间的距离,不确定性U定义为实际性能值的不确定性,此处性能阈值为确定值,不确定性仅指设计点不确定性,如图3 所示。取设计区间的中值为设计点,则性能裕量为许用位移值和设计区间的中值之差,不确定性为设计区间的半宽度,其具体表达式如下:

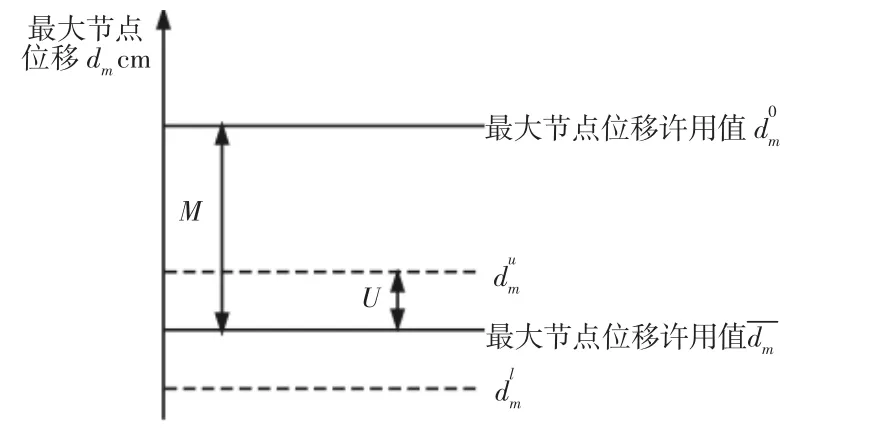
图3 最大节点位移性能通道Fig.3 Performance Gate of Maximum Node Displacement
基于QMU 的可靠性评价方法用置信因子CF 来表征结构是否可靠。其定义是关键性能参数的裕量M 和不确定度U 之比:

4 基于LSF 和QMU 的可靠性拓扑优化方法
4.1 优化模型
关注的问题是:针对任意结构,考虑其材料参数及载荷具有区间不确定性,以结构最大刚度为优化目标、结构可靠性为约束条件,进行结构的拓扑优化获得最优结构。针对该问题的基本思路是:基于LSF 进行结构拓扑优化,优化迭代过程中利用QMU方法计算结构的可靠性约束,并将该约束作为确定优化方向的依据。
基于上述思路,假设结构设计区域为ΩFDDM,设计变量为紧支径向基函数的插值系数p,建立以插值系数为设计变量,以结构最小应变能为目标,以结构体积为普通约束,以位移的QMU置信因子为可靠性约束,则具有区间不确定性结构的可靠性拓扑优化数学模型为:
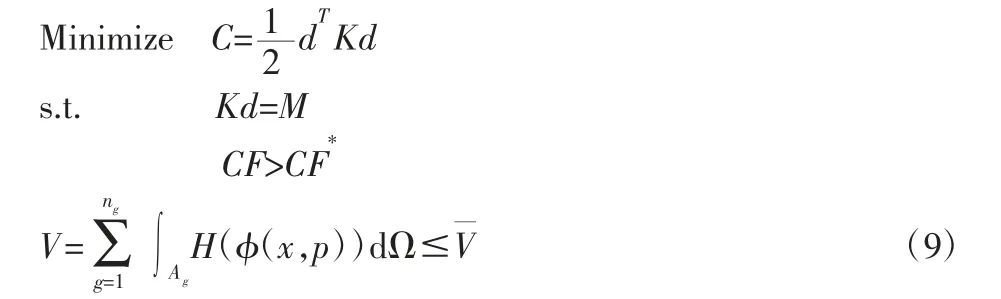

式中:C—结构应变能,是结构总刚度的逆的度量,即为平均柔度;d—结构的节点位移向量;K—结构整体刚度矩阵;F—结构所受外载荷;CF—衡量结构可靠性的置信因子;CF*—给定的大于1 的置信因子;ng—对结构进行B 样条有限胞元分析时的胞元数;Ag、kg—第g 个胞元的区域和刚度矩阵;—结构体积及其上限;D、B—结构的弹性矩阵和应变矩阵;φ(x,p)—式定义的LSF。
4.2 求解策略
使用QMU 方法进行可靠性分析,求出位移置信因子CF 后,借助水平集函数建立参数化的数学模型,然后使用MMA 方法求解。整个优化求解的重点是刚度矩阵对设计变量的灵敏度求解,目标和约束的灵敏度均可由其推导得到,而刚度矩阵K 则由各个胞元的刚度矩阵kg组装得到,其表达式如式所示。由于弹性矩阵D 和应变矩阵B 均与设计变量无关,则kg对第i 个设计变量pi的灵敏度为:

优化模型中目标应变能C 对第i 个设计变量pi的灵敏度为:

结构所承受载荷F 和设计变量无关,因此∂F/∂pi=0,则位移d 对第i 个设计变量pi的灵敏度为:

将式代入式中,可进一步化简得到:

优化模型中可靠性约束CF 对第i 个设计变量pi的灵敏度为:

从式和可以看出,应变能C 和置信因子CF 的灵敏度分析问题均转化为了刚度矩阵K 的灵敏度分析问题,结合前面推导可求出相应的灵敏度。
从体积V 的表达式可知约束函数V 对第i 个设计变量pi的灵敏度和刚度矩阵灵敏度求解类似,每个胞元对应的体积Vg的灵敏度求解如下:

根据求解得到的各变量的灵敏度信息,使用MMA 算法即可完成结构的可靠性拓扑优化。整个可靠性拓扑优化的流程,如图4 所示。

图4 基于LSF 和QMU 的结构可靠性拓扑优化流程图Fig.4 Flowchart of RBTO Based on LSF and QMU
5 数值算例
以拓扑优化中经典的悬臂梁结构为例,进行可靠性拓扑优化,验证其有效性。具体结构,如图5 所示。其长12cm,宽6cm,厚0.1cm,结构材料为各向同性材料,泊松比为0.3,弹性模量E 具有区间不确定性,其值为[0.8,1.2]GPa,悬臂梁自由端受一竖直向下的区间载荷F 的作用,其值为[0.8,1.2]kN,给定结构关键性能参数节点最大位移的许用值为3cm,结构保留材料的体积上限为3.6cm3。
结构初始设计区域被划分为80×40 个矩形胞元。根据E 和F 的值,求出表征可靠度的置信因子CF,给定的置信因子为1.2(CF*=1.2)。按照式所示,建立悬臂梁的可靠性拓扑优化模型,使用移动渐近线算法(MMA)进行优化求解,迭代终止条件为:设计变量的累积变化量小于0.001。拓扑优化的过程,如图6 所示。悬臂梁拓扑优化的初始设计结构,为了加快迭代的收敛速度,在设计区域内预先均布若干圆孔,如图6(a)所示。使用这里所述可靠性拓扑优化方法进行拓扑优化的迭代过程及达到收敛时的最终结果,如图6(b)~图6(d)所示。整个拓扑优化过程中应变能的迭代历程,如图7 所示。从图中可以看出应变能从25 步开始已经基本收敛,最终收敛时应变能为61.67N·cm,保留体积为3.598cm3,此时置信因子为3.814,满足约束条件,结构可靠。

图5 悬臂梁结构的设计区域Fig.5 Design Domain of a Cantilever Beam

图6 悬臂梁结构的可靠性拓扑优化设计Fig.6 Reliability-Based Topology Optimization of the Cantilever Beam
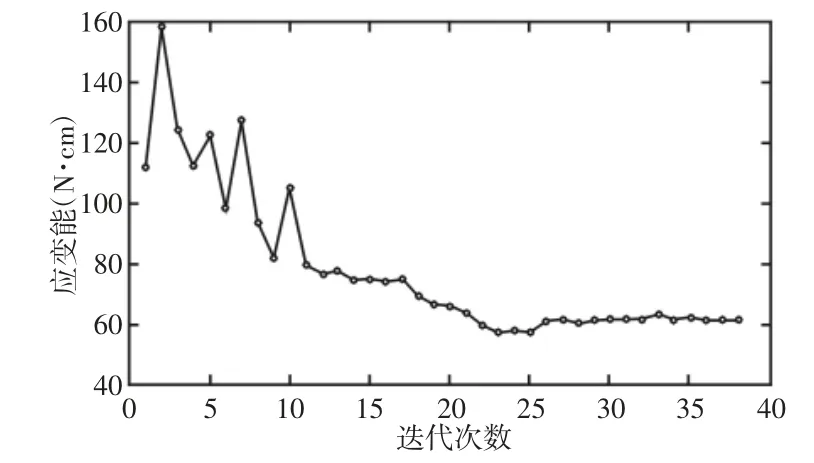
图7 应变能变化历程Fig.7 History of Strain Energy Change
从拓扑优化的最终结果可以看出:使用文中的可靠性拓扑优化方法可以得到一个清晰且合理的拓扑结构,表明使用的拓扑优化方法可以很好地避免拓扑优化中常见的灰度单元、棋盘格式和网格依赖性等数值问题。同时,在拓扑优化过程中考虑了输入参数的区间不确定性,保证了最终的拓扑优化结果的可靠性,拓扑优化的结果更符合工程实际,更具参考价值。
6 结论
针对具有区间不确定性的结构可靠性拓扑优化问题,利用水平集函数的特性,以裕量与不确定性量化(QMU)置信因子为可靠性约束,建立了基于水平集函数的结构可靠性拓扑优化模型,并使用移动渐近线算法(MMA)进行求解。数值算例的结果表明文中建立的优化模型和使用的求解方法是可行且有效的。通过此研究,一方面对这种新的拓扑优化方法进行了扩展,考虑了输入参数的区间不确定性,使结果更符合工程实际;另一面将这种新方法和可靠性分析结合,为区间不确定性结构的可靠性拓扑优化的研究提供了一种可行方法。
