基于多尺度熵和EMD 阈值的电能表内异物声音信号去噪方法
2020-12-25欧习洋
张 进,吴 健,欧习洋,欧 熙
(1.国网重庆市电力公司电力科学研究院,重庆401120;2.四川福德机器人股份有限公司,四川 绵阳 621000)
1 引言
随着近几年国家智能电网和电力用户信息采集系统建设,电子式交流电能表得到了广泛的应用。为确保计量器具的精确性与可靠性,电能表在用于计量之前都必需经过一整套检定项目的测试[1]。在“JJG596-2012 电子式交流电能表检定规程”中,异物检测是外观检测项目的一个子项,其目的是检测电能表内部是否存在焊渣残留、松脂残留、脱落元器件、胶沫等异物或杂物。传统的电能表内异物检测采用“手摇+耳听”的人工检测方法。异物自动检测装置通过设计自动摇表结构和自动控制系统实现自动摇表和声音采集,利用声音识别技术实现异物检测算法。由于摇表装置结构复杂,环境噪声成分较多,电能表内异物声音信号在采集过程必须采用合适的去噪方法排除噪声干扰。由于异物自动检测装置采集的声音信号是典型的非线性非平稳时变信号,频率成分非常复杂,对去噪方法研究带来了挑战。
小波分析作为新的时频分析工具,具有良好的自适应性,并迅速应用到信号去噪中。小波阈值去噪继承了小波分析的多分辨率特性,方法简单且计算量小,是一种应用比较广泛的去噪方法。但小波变换的相关参数如小波阈值的确定、小波基函数的选择、信号的分解层数都需要根据信号分解后的具体情况凭经验人为地选定,这使得去噪过程更加复杂化[2]。
经验模态分解法是由Huang 等人提出的一种新的信号分解方法,该算法将待处理的原始信号唯一地分解为一系列本征模态函数(intrinsic mode function,IMF)集,每个本征模态函数都包含了原信号的部分频率成分,其频率成分随信号本身的变化而变化。该方法根据信号本身的特性自适应地分解成合适的模态,而这些模态很好地反映了信号在不同时间局部的频率特性。它不但具有小波分析多分辨率分析的特点,而且克服了小波基以及分解层数选择的困难。
文献[3]将相关系数和EMD 区间阈值结合起来,通过原始信号与IMF 分量的相关系数来选取相关模式,最后进行阈值去噪,取得了较好的效果。文献[4]将EMD 同小波阈值结合起来,通过自适应选择EMD 分解后的IMF 分量,结合小波阈值对脉搏信号进行处理,对于脉搏信号的噪声消除有较好的的效果。文献[5]采用EMD 方法对柴油机振动信号进行处理,较好地消除了干扰因素的影响。文献[6]提出了EMD 与小波收缩相结合的方法对含有背景噪声的滚动轴承信号进行了预处理,并且同基于互相关系数和峭度准则的EMD 方法进行了比较,结果表明EMD 同小波收缩相结合的方法在低信噪比时能更好地保留轴承信号。单独使用EMD 或者小波阈值法都不能取得很好的效果,文献中的噪声特性也不能直接适用于电能表内异物声音信号去噪方法,因此需要研究电能表内异物声音信号的噪声特性,针对性地研究一种更为有效地电能表内异物声音信号背景噪声去除的方法。
结合了短时能量、多尺度熵、改进小波阈值和EMD 去噪方法,研究了一种基于多尺度熵和EMD 阈值的电能表内异物声音信号去噪方法。通过对添加了不同信噪比的电能表内异物声音信号进行模拟测试,对所提方法同传统的EMD 去噪方法进行了效果比较,证明方法在电能表异物声音信号噪声去除方面更为有效。
2 基于短时能量、多尺度熵和EMD 阈值的降噪
异物声音信号降噪方法框图,如图1 所示。首先采用短时能量提取信号关键帧后,进行EMD 分解并计算各个本征模态函数的多尺度熵值,根据多尺度熵值选择一部分IMF 分量进行处理;最后将去噪后的IMF 分量、未进行处理的IMF 分量以及EMD 分解得到的残差进行信号重建,从而得到更准确的去噪后的信号。

图1 基于短时能量、多尺度熵和EMD 的电能表内异物声音信号去噪方法Fig.1 Denoising of Foreign Body Sound Signals in Electric Energy Meters Based on Short-Term Energy,Multi-Scale Entropy and EMD
2.1 短时能量提取数据
电能表内异物声音信号的能量随着时间变化比较明显,异物与电能表内部碰撞时其能量变化明显较大。采集的声音数据一般较长,为了提高处理速度,可对采集的数据设置合适的帧长进行分帧,利用短时能量提取出关键帧数据进行后续处理。根据采集的数据设置帧长为100ms,对于电能表内异物声音信号的短时能量,其计算方法如下:

式中:fn—对采集的电能表内异物声音数据进行分帧以后的帧数;L—每帧数据的帧长。
2.2 多尺度熵区分IMF 分量的复杂度
传统的样本熵仅仅只能反映信号某一尺度下的特征,文献[7]提出的多尺度熵(Multiscale Entropy,MSE)可以用来反映信号在不同的时间尺度下的复杂程度。信号越是复杂不规则,生成新模式的机率越大,多尺度熵值也就更大[8]。
对于采集的电能表内异物声音信号,经过EMD 分解后,各阶IMF 由于背景噪声的存在复杂程度不一,可用多尺度熵来量化信号的非线性和非平稳特性。越复杂的信号多尺度熵值越大,故可由计算得到的各阶IMF 分量多尺度熵值设定一个阈值,一般选择相邻两阶IMF 分量多尺度熵值变化较大的那一阶多尺度熵值为阈值。对大于阈值的IMF 分量进行进一步的处理,从而更好地完成信号的去噪。具体计算过程如下:
(1)对于时间序列{y(t),t=1,2,…,M},采用下式重新构造粗粒化的序列{u(t),t=1,2,…,N},其中τ 表示尺度,N=int(M/τ)为重构后时间序列的长度(int 表示取整)。

(2)设定模式维数m 和相似容限r,按照如下公式构造m 维矢向量x(i)。

(3)定义向量x(i)(1≤i≤N-m+1)与x(j)(1≤j≤N-m+1,j≠i)之间的距离为两者对应元素中差值最大的一个,即:
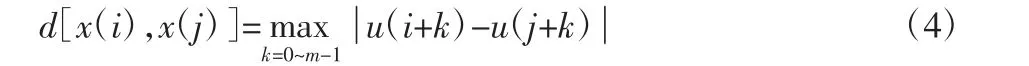
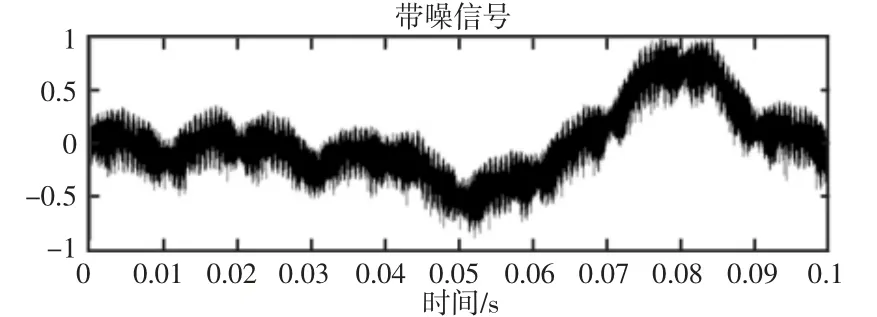
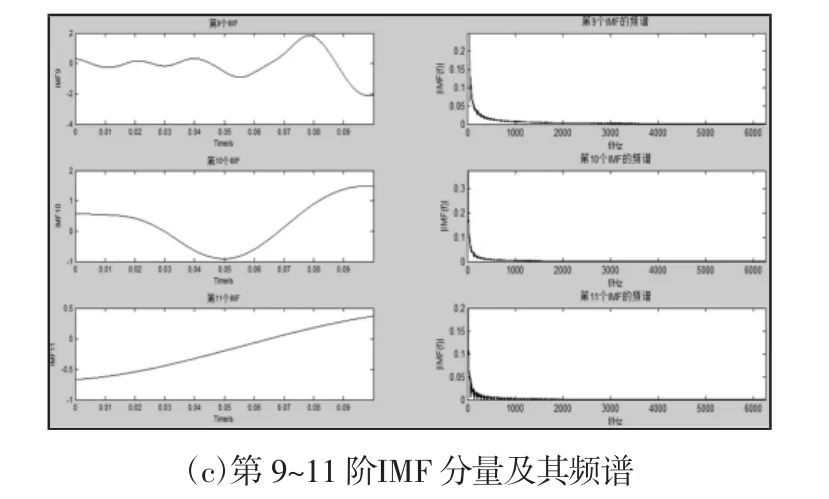
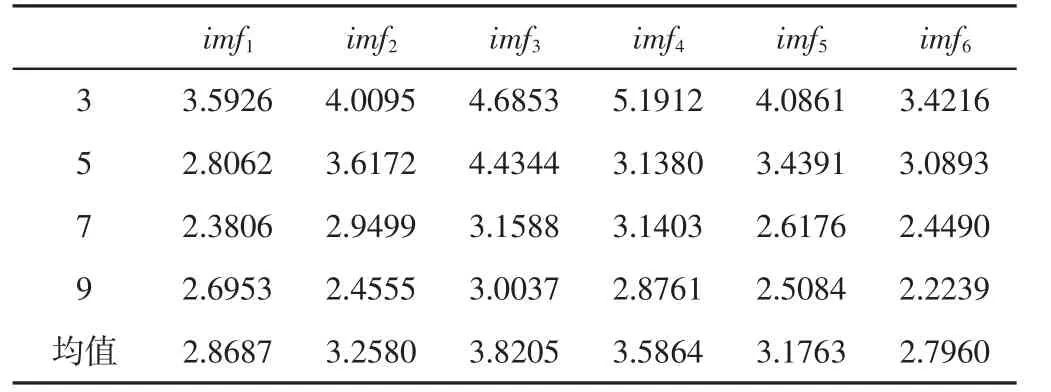
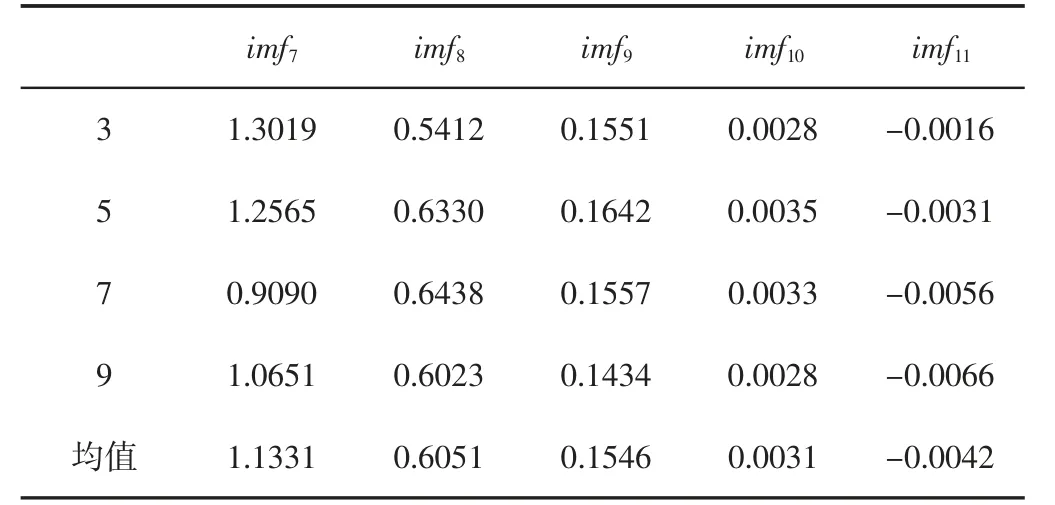
(4)根据给定的相似容量r(r>0)以及每个i(1≤i≤N-m+1)值,分别计算距离d[x(i),x(j)] “坦率他说,我虽然并不了解您,但我觉得您绝不是罗马那些无聊透顶的有钱人可比的,您身上有一种莫名其妙的气质吸引我。 (5)按照如下公式计算步骤(4)中计算结果的平均值φm(r)。 (6)令m=m+1,重复上述四步,计算φm+1(r)。 (7)时间序列{u(t),t=1,2,…,N}的样本熵计算公式如下。 (8)根据上述计算过程(1)~(7),计算各个尺度τ 下的样本熵,从而得到一组多尺度熵。 根据上述计算过程可知,多尺度熵与模式维数m、相似容限r、粗粒化后的数据长度N 以及尺度τ 有关[8]。模式维数m 的增大会导致重构向量x(i)包含的信息越多,与此同时m 的大小也与数据序列的长度成正比。相似容限r 偏小会造成统计特征信息的缺失;偏小又会导致统计特性对噪声敏感。多尺度熵对数据长短要求并不高,若m=2,则N=90~900 即可。对于尺度因子τ,可以选择为(1~20)范围之内。根据实际选择m=1,N=1000,r=0.01,尺度因子τ=3,5,7,9。 2.3.1 EMD 分解 EMD 信号分解算法的目的是针对非线性非平稳信号做一个分解得到一系列表示信号在相异特征时间尺度的固有模态函数分量,使每个模态函数是窄带信号,从而可以进行希尔伯特谱分析。IMF 分量的获取可以视为一个自适应的筛选过程。 (1)确定数据序列x(t)极大值集和极小值集,由极大极小值集合确定上下包络线,算出上下包络线的平均值m1(t)。 (2)计算h1(t)=x(t)-m1(t),检查h1(t)是否满足IMF 分量的筛选条件,若满足则继续进行下一阶分量的分解,反之,将h1(t)作为一个新信号继续重复进行前面的流程直到h1n(t)满足条件,直到得到第一个IMF 分量g1(t)=h1n(t)。 (3)将r1(t)=x(t)-g1(t)作为新的信号重复步骤(1)~步骤(2)得到g2(t)。同理依次可得到各阶固有模态函数以及余项rn(t)。余项满足单调性或者仅存在一个极值点。 (4)原始信号经过EMD 分解最终可表示为: 经过分解获得了n 个本征模态函数和残差,分解得到的各阶IMF 分量代表了原始信号中相异时间尺度的特征信号,并且是窄带信号,使得瞬时频率分析具有了意义。 2.3.2 EMD 的滤波特性 EMD 方法通过将非线性非平稳的原始信号自适应地分解为一系列表征信号不同特征时间尺度的IMF 分量,这个分解过程也是一个多分辨率分析滤波分解过程。每一个IMF 分量包含了原信号不同的特征尺度以及频率成分,因此可以利用这个特征设计一种基于局部特征时间尺度参数的时空滤波器(time-space filter)。当含噪原始信号x(t)经过EMD 分解后,信号可表示为: 此时,低通滤波器可以表示为: 高通滤波器则可表示为: 带通滤波器可表示为: 式(11)~式(13)中的k 为滤波器的滤波截断参数,其取值一般根据信号分解后的情况灵活确定。时空滤波器基于信号EMD分解后的本征模态函数,因此这种滤波器能够充分保存信号本身的非平稳特征和非线性特性[2],一般可以取得较好的效果。 采用EMD 算法构造的时空滤波器多针对于IMF 分量中噪声与有用信号不重叠的情况,但是对于有用信号同噪声在IMF分量中频率混叠的情况,直接采用上述去噪方法便会导致一部分有用信号被当成噪声去掉。电能表内异物声音信号经过EMD 分解后部分低阶IMF 分量将存在噪声与有用信号混合的情况。由此,可先根据多尺度熵确定出噪声与有用信号混合相对复杂的IMF 分量,对这些分量结合小波阈值处理后进行信号重构,这个过程称为EMD 阈值降噪。 采用软阈值处理,具体为: 阈值THri的计算公式如下: 各个IMF 所含噪声的标准差为σi,由式(16)计算而来,L 为各阶本征模态函数的长度。 我们对大于设定的多尺度熵阈值的IMF 分量进行阈值去噪得到Ci(t),将处理后的Ci(t)、无需经过处理的IMF 分量以及EMD 分解得到的残差叠加重构即可得到去噪后的信号。 分别采集了较为纯净的电能表内异物声音信号以及工厂的背景噪声。针对采集到的数据设计了两组实验。将采集的工厂背景噪声按照设定的信噪比(-5dB、0dB、5dB)叠加到较为纯净的电能表内异物声音信号中,分别针对两种方法设计实验。实验1 是采用传统的EMD 去噪方法对纯净的电能表内异物声音信号混合工厂背景噪声以后的信号进行去噪实验。实验2 是采用提出的方法对较为纯净的电能表内异物声音信号混合工厂背景噪声以后的信号进行去噪实验。实验采集装置整体结构外观图,如图2 所示。采集的原始电能表内异物声音信号,如图3 所示。加入工厂背景噪声以后的混合信号,如图4 所示。对混合信号进行EMD 分解以后的各阶IMF 分量及其频谱,如图5 所示。实验1 采用传统的EMD 去噪方法,即构造一个时空滤波器,直接去掉一部分IMF 分量,再将余下的IMF 分量重构。由以上分解可知,噪声主要集中在前两阶模态函数分量。故构造一个高通滤波器,实现电能表内异物声音信号的去噪,去噪效果,如图6 所示。 图2 声音信号采集装置外观图Fig.2 Appearance of Sound Signal Acquisition Device 图3 原始信号Fig.3 Original Signal 图4 带噪信号(信噪比=5dB)Fig.4 Noisy Signal(snr=5dB) 图5 第1~11 阶IMF 分量及其频谱Fig.5 Stage 1 to 11 IMF Components and Their Frequency Spectrum 图6 传统的EMD 去噪后信号Fig.6 Traditional EMD Denoising Signal 实验2 采用提出的方法,不同尺度下各阶IMF 分量的多尺度熵均值,如图7 所示。不同尺度下各阶IMF 分量的多尺度熵值及均值,如表1~表2 所示。根据图7 计算相邻两阶多尺度熵均值的变化斜率,第6 阶至第7 阶的斜率变化最大,值为1.6629,即前面6 阶的IMF 分量同后面的IMF 分量所构成的信息空间区别较大,结合前面的频谱图可知,前面6 阶包含了较多的异物声音信息及其他噪声信息,故根据相邻IMF 分量多尺度熵均值变化斜率设置阈值,选择斜率突变最大处的IMF 分量的多尺度熵均值为阈值,对大于此阈值的分量进行去噪处理,小于此阈值的IMF分量不做处理,最后将去噪后的IMF 分量、未去噪的IMF 分量以及EMD 分解余下的残差叠加重构,完成信号去噪。采用提出的算法的去噪效果,如图8 所示。采用两种方法去噪以后的信噪比(SNR)以及均方差(MSE),如表3 所示。 图7 各阶IMF 的多尺度熵均值Fig.7 Multiscale Entropy Mean Value of Various Order IMFs 表1 尺度3、5、7、9 下第1 至第6 阶IMF 的多尺度熵值及均值Tab.1 Multiscale Entropy and Mean of the 1st to 6th IMFs at Scales 3,5,7 and 9 表2 尺度3、5、7、9 下第6 阶后各阶IMF 的多尺度熵值及均值Tab.2 Multiscale Entropy and Mean Value of IMF After Stage 6 in Scales 3,5,7,9 图8 EMD 阈值去噪后信号Fig.8 EMD Threshold Denoising Signal 表3 两种去噪算法对应的去噪结果评价指标Tab.3 Corresponding Denoising Results of Two Denoising Algorithms 根据多尺度熵以及EMD 的滤波特性,结合小波阈值提出了一种基于多尺度熵和EMD 阈值的电能表内异物声音信号去噪法。该方法对含噪电能表内异物声音信号处理后信噪比明显提高,均方差也有显著地减小。与传统的EMD 滤波算法相比较,该算法同小波阈值去噪法相比较,去噪原理简单易行,避免了小波基函数的选择、分解层数等参数的确定;同传统EMD 去噪算法相比较避免了IMF 分量选取的盲目性,阈值根据分解后的IMF 分量的多尺度熵均值的斜率变化进行设置,针对不同的声音数据,可以自适应的更改阈值,避免了人为的选择,能够在一定程度上自适应地去除噪声,在电能表内异物声音信号去噪方面有很好的效果。



2.3 EMD 分解及其滤波方法





2.4 基于多尺度熵与EMD 的阈值去噪方法



3 实验验证







4 结语
