基于LinWPSO算法的同步顶升系统模糊PID控制器设计
2020-12-25刘鑫蔡改贫罗小燕
刘鑫,蔡改贫,罗小燕
(江西理工大学 机电工程学院,江西 赣州 341000)
0 引 言
液压同步顶升系统集成了液压技术、机械结构、计算机算法和电气自动化控制等先进理论技术,是与桥梁改造、建筑施工和起重吊装相结合的一种新型的施工技术装备,成功应用在桥梁的改造、重要建筑物的保护性迁移等方面,并取得了良好的经济效益[1-3]。
大型机械设备的制造、使用以及在役一段时间后的检修能力往往代表着国家的工业发展水平,其中,在检修过程中,大质量部件的高精度、安全、高效吊装与分离是关键[4]。近年来,针对顶升系统同步控制问题,国内外学者开展了很多研究:吕国芳等[5]针对青岛中国海洋石油总公司装载级改造工程,提出一种基于PLC的液压同步升降控制系统,该系统通过控制电液比例减压阀的开口压力,调节油液流量,进而实现同步顶升,并使用灰色预测模糊控制算法降低同步误差,将其应用至实际工程中进行试验分析,结果表明,所设计的系统控制性能较好,达到了预期的目标;刘学伟[6]针对分布式液压同步控制系统,采用模糊自整定P闭环控制和前馈开环控制的综合方法,实现了在“同等方式”下的位移同步;周玉伟等[7]针对大型机械物件连续同步顶升存在的问题,采用多个桩腿多油缸同步顶升的方法,支点与支点间通过同步分流液压泵的容积同步进行控制,桩腿间采用基于位移模糊的多点主从同步控制方式,结果表明,该控制方法满足同步要求,适用于实际工况环境。
上述研究成果都是采用模糊控制实现多油缸的同步顶升,但同步精度和速度不能满足现代液压同步顶升系统的需要。因此,寻找一种智能算法对模糊控制器进行优化,就显得非常必要和迫切。粒子群优化(particle swarm optimization,PSO)算法是一种仿生智能算法,常常用于性能参数的优化。相比其他寻优算法,LinWPSO算法不容易陷入局部最优、搜索能力更强、收敛更快,采用这种算法优化,可以使同步顶升系统获得更高的同步精度。
由于大型挖掘机液压顶升系统具有体积大、干扰因素多、质量大等特点,在实际工况中,顶升同步精度要求较高。本文结合工程实际背景(同步精度控制在±1 mm),采用几何分析计算的方法,验证顶升体系的同步精度要求,设计模糊PID同步顶升控制器,并引入LinWPSO算法对模糊控制器的性能参数进行优化。建立AMEsim液压仿真模型和多液压缸同步顶升Simulink控制系统模型,并进行联合仿真研究。采用本文提出的方法对WK-35大型挖掘机上下盘分离同步顶升工程进行现场试验研究,并对所设计的改进模糊PID控制器的可行性进行验证。
1 工程背景
本文研究背景为江西铜业集团公司德兴铜矿实际大修现场。型号为WK-35的挖掘机在大修的上下盘分离工序中,整个分离过程极为重要的一点就是要确保上盘结构的完整性,不能因为重量不均而使上盘的顶升、下放过程不稳定,出现倾斜,导致上盘中央枢轴铜套与中央枢轴相互卡死,甚至造成上盘倾翻而损坏,进而造成人员伤亡。
WK-35大型挖掘机上下盘分离操作现场如图1所示。

图1 WK-35大型挖掘机上下盘分离操作现场Fig.1 WK-35 large excavator disconnect operation scene
根据设计要求和现场工况条件,该项工程存在以下特点:顶升质量大,在5.51×105kg以上,且质量分布不均匀;顶升高度很大,要求将上盘相对下盘顶升1 700 mm的距离,且一次顶升到位;多点同步顶升,顶升点的布置难度大;顶升精度要求高,系统稳定性要好。
具体顶升过程为:顶升准备→预顶升→设定每次行程、同步精度→同步顶升→加上辅助支撑→判断是否到达→重复顶升到达设计高度→加上辅助支撑→移出下盘→逐级减辅助支撑→缓慢回落→辅助支撑稳定上盘→顶升完毕。
2 顶升体系分析
在上下盘顶升分离时,为防止悬臂、斗杆、铲斗等活动部件因摇晃而产生倾覆,在分离施工前对其进行拆除,拆除后挖掘机上盘质量约5.51×105kg。上下盘间通过下盘的中央枢轴与上盘的中央枢轴孔间隙配合,最大间隙0.5 mm,配合深度1 400 mm,设计顶升系统的同步精度±1 mm,顶升过程中央枢轴与顶升平面几何关系如图2所示。

图2 顶升过程中央枢轴与顶升平面的几何关系Fig.2 Geometric relationship between the central pivot and the elevation plane in the uplift process
图2中顶升点间的距离为L,中央枢轴配合深度为S,理想的同步顶升状态下,中央枢轴与水平的顶升平面垂直,与中央枢轴配合的上盘孔的轴线与中央枢轴平行,假设间隙最大为0.5 mm;当出现顶升点不同步时,顶升平面倾斜,上盘的孔与中央枢轴形成如图1所示的α夹角,顶升点间出现顶升高度差Δh,轴与孔间的最大间距Δsmax=1 mm。一般用同步误差表示同步精度,其表达式为
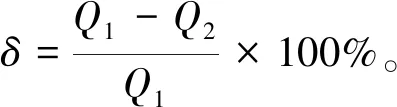
(1)
顶升平面倾斜时,α=β,因此,Δh=tanβ·L=tanα·L,在WK-35大型挖掘机上盘同步顶升过程中,L=13 693 mm,因此,从几何关系的角度看,最大顶升-下降同步精度为
δmax=Δhmax=tanα·L=
1/1400×13 693=9.78,
(2)
因此,±1mm的同步精度设计要求满足从几何关系角度所得同步精度要求。
3 LinWPSO算法及模糊PID同步顶升控制
3.1 模糊PID同步顶升控制器
多液压缸顶升系统的模型参数具有不确定性和非线性性,无法建立精确的数学模型。经典、现代控制理论均无法应用于这类系统,而以模糊集合论、模糊语言以及模糊推理等为理论基础的模糊控制为此类问题的解决提供了一个有效的方案[8-10]。模糊控制是基于模糊算法的一种优化控制算法,依靠试验获得的现成经验或者专家指导的策略形成规则,进而控制输入和输出,实现复杂非线性系统的模糊控制。模糊控制的算法核心是模糊处理和模糊推理,其中模糊处理包括模糊化和清晰化。
模糊PID同步顶升控制器包括PID顶升控制部分和模糊控制部分,其系统原理如图3所示。

图3 模糊PID同步顶升控制系统原理Fig.3 Principle diagram of fuzzy PID synchronous lifting control system
同步顶升系统模糊PID控制器的目标是控制比例伺服阀,从而保证液压缸的精准定位以及多点同步顶升。模糊控制主要是把模糊化后的系统偏差e及偏差变化率ec作为输入,按照已制定好的模糊规则表,通过模糊化、模糊推理、清晰化得到精准的控制量u,同时获取PID控制参数的增量ΔKP,ΔKI,ΔKD,从而实现对PID 3个控制参数的调整,完成KP,KI,KD的自动调节。图4所示为同步顶升系统模糊PID控制流程。

图4 模糊PID控制流程Fig.4 Fuzzy PID control flow
影响模糊PID控制器性能好坏的最主要因素是隶属函数,隶属函数曲线的形状特征表征着模糊控制器的控制性能:形状尖的模糊子集控制力度大,灵敏度高;形状平缓则灵敏度低,控制系统更稳定。通过对隶属函数进行动态优化,可以使模糊PID控制器的控制性能达到最佳。本文采用三角型隶属函数,表达式为
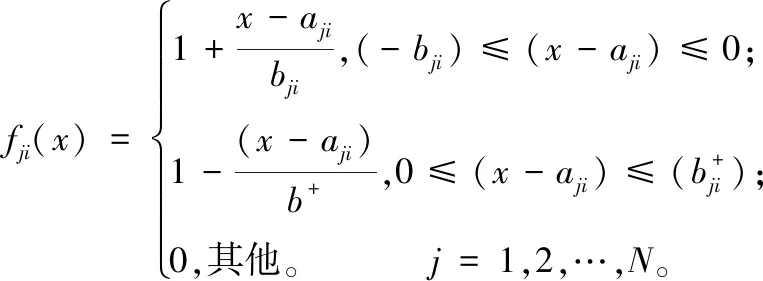
(3)
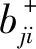
因此,需要对模糊控制器的性能参数进行优化,使同步顶升模糊PID控制器的性能最优。
3.2 改进PSO算法
粒子群优化算法(PSO)是由Kennedy和Eberhart博士提出的一种群体智能优化算法,因其简单易于实现、智能程度较高等特点,广泛应用于各个领域,成为复杂问题寻优的重要解决手段[11-12]。
PSO算法基本原理如下。
假设需要优化的变量个数为D,粒子群的粒子总数为N,定义Xp=(xp1,xp2,...,xpD)、Vp=(vp1,vp2,...,vpD)分别为粒子群中第p个粒子的位置和速度,Wp=(wp1,wp2,...,wpD)为粒子群中第p个粒子自身达到最优时的位置,Wg=(wg1,wg2,...,wgD)为整个粒子群达到最优时的位置,则粒子群算法的速度与位置更新公式为
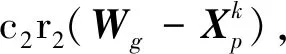
(4)

(5)
式中:k为迭代次数;ω为粒子惯性权重;c1,c2为粒子的学习因子,前者为个体,后者为全局;r1,r2为[0,1]内的随机数,表示粒子的独立多样性。
利用式(4)~(5)可实现对个体极值及群体极值的跟踪,并通过不断迭代更新,满足终止条件时可使粒子群全局都趋近于最优位置Wg。传统的粒子群算法虽然可以达到收敛,但是随着迭代次数的增加,粒子群算法常常出现无法跳出局部解的情况。另外,传统粒子群算法收敛不够迅速,无法很快达到最优解。
针对上述传统粒子群算法存在的问题,对PSO算法进行改进,提出权重线性递减的LinWPSO算法。权重因子ω大时,粒子不容易陷入局部最优,有利于全局搜索;权重因子ω小时,粒子在当前区域寻优的精度更高,有利于快速收敛。利用LinWPSO算法这一特点,采用线性变化的权重,使得ω的值在全局范围内从ωmax线性减小为ωmin。权重因子ω随时间的变化公式为

(6)
3.3 基于LinWPSO算法的模糊PID同步顶升控制器
LinWPSO算法具有自适应能力强的特点,对于同步顶升模糊PID控制器的多参数,优化效果非常显著。
本文所用的模糊控制中,隶属函数共有9个参数,假设分别是αi,βi,γi(i=1,2,3),把这9个参数作为粒子群的粒子进行优化,以达到优化模糊PID控制器的目的。具体流程如下。
步骤一:在整个搜索空间初始化粒子群,随机获得每个粒子的初始位置和速度。
步骤二:利用适应度函数对每一个粒子的适宜值作出评价,并以此决定粒子所在位置的优劣。
步骤三:根据适宜值,通过与搜索过的最佳解pbest比较,搜寻出每个粒子当前的最佳解pbest;通过与全局历史最佳解gbest比较,搜寻出整个粒子群在本次迭代中的最佳解gbest。
步骤四:按照LinWPSO算法公式(3)~(5),对该粒子位置和速度更新。
步骤五:如果未获得理想解或者不足达到迭代结束条件,则返回步骤步骤二,循环继续,直至满足要求,算法结束。
采用LinWPSO算法对多液压缸同步顶升模糊PID控制器的参数进行优化,其流程如图5所示。将粒子数和迭代次数均设置为100,算法学习因子c1,c2均设置为1.2。根据上述条件,对LinWPSO算法进行优化仿真,结果如图6所示。
由图6寻优过程中适宜值的变化曲线可知,在第7代左右,权重因子ω较大,此时下降速度很快;随着ω的减小,第20代开始,搜索精度逐渐增大,最终在第48代时寻到最优解,算法的寻优速度和寻优精度都得到提升。
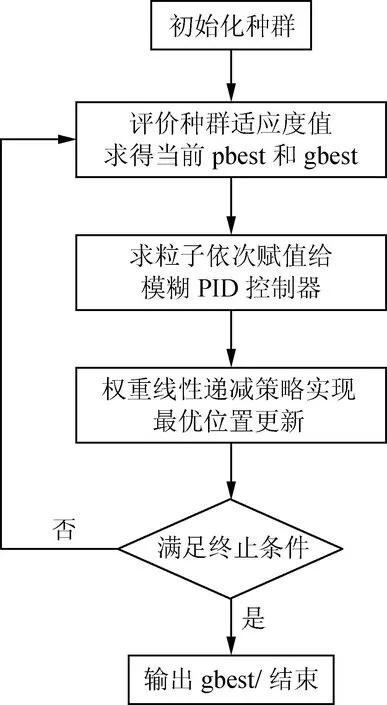
图5 改进PSO算法流程Fig.5 Improved PSO algorithm flow

图6 LinWPSO算法收敛曲线Fig.6 Convergence curve of LinWPSO algorithm
4 同步顶升系统仿真研究
AMEsim在液压建模和仿真方面功能强大,且模型具有很高的精度,而MATLAB/Simulink对于智能算法的实现以及控制器的模拟仿真具有很大优势。因此,通过AMEsim/MATLAB联合仿真,可以实现优势互补,解决以往单一软件仿真存在的不足。
4.1 AMEsim模型的建立
AMESim(advanced modeling environment for performing simulation of engineering systems)是集成了机械、液压、气动、热、电和磁等领域的综合性液压系统仿真软件,为液压系统的计算机模拟仿真提供了强大的支持[13]。AMESim已经成功应用于航空航天、车辆、船舶、工程机械等多学科领域,成为流体、机械、热分析、电气、电磁以及控制等复杂系统建模和仿真的优选平台[14-15]。
在AMESim软件中,由于缺少多通道的液压控制阀和液压控制泵等模型,所以在模型构建过程中,使用电信号单元代替液压信号,部分液压元件的控制由电信号进行控制。所构建的WK-35大型挖掘机上下盘分离同步顶升液压系统AMESim仿真模型如图7所示。

1-位置传感器;2-长行程双作用液压油缸;3-压力传感器;4-平衡控制阀块;5-节流调速阀;6-安全阀;7-油液属性;8-两位两通电磁阀;9-电信号;10-三位四通电磁阀;11-溢流阀;12-高压柱塞泵;13-电动机;14-滤油器;15-油箱
图7 同步顶升AMESim仿真模型
Fig.7 Synchronous uplift AMESim simulation model
为验证所建模型的有效性,以WK-35大型挖掘机4点同步顶升油缸上升工作时的动态过程为研究对象,按照图7模型进行AMEsim仿真。液压系统采用双液压油泵提供动力,通过初步设计,采用单泵5 L/min的供油速度。为了更好地模拟和研究不同现场环境下工作时挖掘机的运行动态特性,分别模拟仿真负重600,700,800 t时油缸活塞速度和油液流速的响应曲线,其动态特性的响应规律如图8所示。
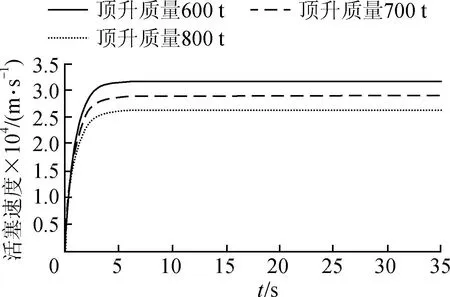
图8 液压单缸活塞速度动态特性Fig.8 Velocity dynamic characteristics of hydraulic single cylinder piston
由图8可知,活塞杆速度在0~5 s内迅速提升至稳态,负重的变化只对最终稳定状态的液压缸活塞速度或者油液流速有影响,稳定后负重600,700,800 t所对应的活塞速度分别为0.32,0.29,0.26 mm/s。液压缸在较短时间内可达到平稳状态,顶升速度稳定。这与WK-35大型挖掘机4点同步顶升油缸上升实际工作时的运动规律基本一致,说明所建立的同步顶升液压系统是有效的。
对负重700 t工况时的单缸顶升位移进行误差分析,结果如图9所示。由仿真结果可知,WK-35大型挖掘机油缸稳定顶升时的位移误差控制在±0.4 mm内,满足系统单缸顶升的控制要求。

图9 液压单缸活塞位移误差仿真结果Fig.9 Simulation results of displacement error of hydraulic single cylinder piston
4.2 模糊PID同步控制仿真模型
多液压缸顶升系统采用“主从方式”控制策略,以1号液压缸活塞杆的位移值作为标准值,对其他3个液压缸进行同步控制。本系统采用4个电液比例换向阀,对每个液压缸活塞杆的伸缩速度进行单独控制,通过调节电液比例换向阀开度的大小,控制液压缸中液压油的流速,使4台液压缸的活塞杆在运动过程中保持一定的同步精度。
在Simulink中建立LinWPSO算法的滑模PID控制系统模型,如图10所示。其中,联合仿真接口模块通过SimuCosim与AMEsim对接,完成顶升位移的输入以及控制指令的输出。

图10 Simulink控制系统模型Fig.10 Simulink control system model
4.3 联合仿真
为了凸显采用LinWPSO算法优化后的模糊PID控制对大型挖掘机顶升时同步精度的影响,对比分析采用模糊PID控制器与本文改进模糊PID控制器2种情形时系统的响应,以验证本文所用方法的优越性。
利用MATLAB中的fuzzy命令将隶属函数和模糊规则写入模型,并通过编程将控制过程写成m文件,通过图10中的S-Function模块导入控制器中,实现对目标量的控制。设置仿真时间为180 s,做出同步顶升液压缸1与液压缸3的顶升位移差曲线以及液压缸2与液压缸4的顶升位移差曲线,如图11(a)所示;在编程时加入LinWPSO算法对模糊PID控制器进行优化,设置同样的参数,可得到结果如图11(b)所示。

图11 顶升液压缸间位移差曲线Fig.11 Displacement difference curves between jacked hydraulic cylinders
由图11可知,不同顶升液压缸之间存在动态变化的位移差,随着顶升位移的增加,顶升位移差也随之增大。采用模糊PID控制器时,位移差值最大可达1.1 mm,已经对WK-35大型挖掘机整体顶升系统性能产生了严重影响;采用LinWPSO算法优化模糊PID器性能参数后,位移差随着时间曲线的变化趋势与采用模糊PID控制器时基本一致,但其值明显降低,顶升最大位移差值只有0.49 mm,大大改善了WK-35大型挖掘机上下盘分离工作时顶升系统的同步控制性能。
5 WK-35大型挖掘机上下盘分离同步顶升工程试验与分析
空载状态下,采用尝试性顶升的方式对系统进行试机调试后,对WK-35大型挖掘机进行上下盘分离同步顶升工程试验研究,预顶升和顶升现场如图12~13所示。

图12 预顶升现场实施图Fig.12 Pre-jacking site implementation diagram

图13 同步顶升现场实施图Fig.13 Synchronous uplift field implementation diagram
在操作屏幕上设置顶升高度为1 700 mm,选取速度平稳后的一个顶升时间段进行试验分析,所测得结果如图14~15所示。由试验结果可得,WK-35大型挖掘机上下盘进行稳定分离时的单缸顶升精度控制在1.2 mm内,而顶升的同步精度控制在1 mm内,液压缸间最大顶升误差为0.91 mm。与仿真结果相比,单缸顶升误差和多缸同步位移差都有略微增大,这是因为在WK-35大型挖掘机上下盘分离的实际工况下,有许多不可忽略的影响因素,如环境因素、阀结构制造误差、液压油条件等。但是现场试验的结果仍在顶升系统的同步精度要求范围内,满足WK-35大型挖掘机上下盘分离时的同步控制要求。

图14 单液压缸顶升时位移误差Fig.14 Displacement error of single hydraulic cylinder during jacking

图15 液压缸间顶升同步位移差Fig.15 Difference in synchronous displacement between hydraulic cylinders
6 结 论
(1)针对WK-35大型挖掘机上下盘分离时不稳定、顶升不同步等问题,设计出基于LinWPSO算法的模糊PID控制器。将粒子群智能寻优理论与模糊PID控制相结合,实现了顶升过程多液压缸位置的高精度同步控制。
(2)通过AMEsim/Simulink联合仿真,对采用模糊PID控制器与LinWPSO算法优化后的模糊PID控制器2种情形时的系统响应进行对比。仿真结果表明,采用LinWPSO算法优化后的模糊PID控制器多液压缸顶升时位移差值明显降低,顶升最大位移差值只有0.49 mm,显著改善了WK-35大型挖掘机上下盘分离时顶升系统的同步控制性能。
(3)进行WK-35大型挖掘机上下盘分离同步顶升工程现场试验研究,结果表明,WK-35大型挖掘机上下盘进行稳定分离时的单缸顶升精度控制在1.2 mm内,多缸间顶升的同步精度控制在1 mm内,满足WK-35大型挖掘机上下盘分离时的同步控制要求。
