基于可靠性分析的军械装备维修策略优化研究

董 理，周奇郑，颜 冰，钟强晖

（海军工程大学 兵器工程学院，湖北 武汉 430033）

0 引言

随着我国海军转型建设逐步深化，对军械装备使用与维修保障提出了更为严格的使用要求，科学合理地制定维修策略[1]，对有效保持其战备完好性，最大限度地降低维修费用，具有重要的经济意义和使用意义。对于军械装备，为了保持其良好的技术状态，使用保障过程中往往采用了定期维修、视情维修、事后维修等相结合的组合维修方式，这种维修策略一般是由相关标准规定的出自经验的传统维修策略[2-3]。随着军械装备新技术、新材料的不断应用，结构越来越复杂，使用模式日趋多样，原有维修策略与装备系统可靠性相脱节的矛盾日益突出，以可靠性为中心的维修策略优化研究成为各行业十分关心的课题。国内外学者在该方面开展了大量的研究，针对不同类型的装备，基于退化轨迹方法和随机过程方法描述其可靠性规律，开展相应的维修策略优化研究，并将研究成果应用到航空、桥梁和核电设备等不同行业中[4-6]。

本文针对有维修活动参与条件下的军械装备部件性能退化规律，研究维修对装备性能状态的影响，并通过定期维护条件下的装备失效过程分析，建立定期维护装备维修策略模型，通过典型组件的维修实例分析，验证模型的有效性。

1 基于性能退化规律的装备失效过程分析

1.1 装备性能退化过程描述

对于退化失效部件而言，如果使用期间没有任何维修活动，则其性能会随着工作时间的增加而逐渐下降（或增加）。下降程度可以通过部件的某些性能状态值（如温度、湿度、电压等）进行度量，通常将性能状态值统称为性能退化量。当部件的性能退化量增加（或降低）到某一数值（或范围）时，则认为部件丧失功能而发生失效。在没有任何维修活动参与时，部件的性能退化过程一般是单调的且具有不可逆性。

维护保养是军械装备的一种常见维修活动，是为保持装备规定状态所需采取的措施，如机械部件润滑、加油、调校等[7-8]，其性能退化过程如图 1所示。研究发现，维护活动不仅会影响装备部件性能退化量的退化进程，而且部分维护活动会将部件的性能退化量恢复到规定值（通常记为0值）。为研究方便，本文所研究的维护活动主要是针对恢复性能退化量到规定值（通常记为 0值）的维护活动，研究这些维护活动对部件性能可靠性规律的影响。

图1 维护条件下装备的性能退化过程示意图Fig.1 Schematic diagram of equipment performance degradation process under maintenance

如上图所示，雷弹部件性能退化量X(t)会在维护时刻被恢复到 0值，随后继续工作，当性能退化量在T时刻达到失效阈值Ls时，部件在T时刻发生失效。由于使用过程中有维护活动参与，导致部件的性能退化过程具有2个特点：1）间断性，性能退化量因为维护而得到恢复，其在维护时刻出现间断点；2）突变性，随着维护次数的增加，每次维护后部件的性能退化量增幅越来越大，性能退化量的变化越来越急剧。

1.2 定期维护装备失效过程分析

根据定期维护装备的使用特点，如图2所示，可以将装备状态分为4种：工作状态o、维护状态s、预防性维修状态m、事后维修状态f。

图2 定期维护装备的工作示意图Fig.2 Schematic diagram of equipment’s regular maintenance

由上图可知，定期维护装备开始正常工作，当达到维护时刻时进行维护。维护时间一般相对于工作时间较短，维护时间可以忽略，维护后装备会继续工作。随着工作时间延长，其故障的可能性会越来越高，通过检测其失效率变化规律而采取预防性维修行为。当然，由于故障的随机性，装备可能在某时刻故障停机，此时，对其进行事后维修。上述使用过程的描述分别对应于a、b两种情况。

为了进一步描述定期维护装备的失效过程，研究时作出以下相关假设。

1）假设装备受到外界因素作用次数服从强度函数为[abtb-1]的非齐次Poisson分布，即装备在时间[t,t+s]内受到外界因素作用数为n的概率满足：

2）外界因素每次作用对装备性能的影响程度与其材料、制造工艺等质量属性有关，所以假设每次外界作用对装备造成的性能状态变化相互独立且服从相同的正态分布：

3）根据上述分析，可以确定装备[t,t+s]时间内的性能状态Xt+s,t与Nt+s,t、Yi有关，综合得到三者的数学关系式为

式中，Nt+s,t、iY分别与装备工作坏境、装备自身属性有关，一般认为两者互相独立。那么，Xt+s,t为一个复合Poisson过程。

4）假设定期维护装备各时刻点的性能状态服从正态分布，根据维护只恢复装备性能状态而不改变装备失效速度的特性，如果记维护时刻为ti(i=1,2,…,m)，那么装备在任意t∈(ti-1,ti]的性能状态X(t,ti-1)满足：

其中，式（4）、式（5）的关系式由复合 Poisson过程的性质获得。

综上所述，可以得到定期维护装备的寿命分布函数为

式中，Ls为失效阈值，当装备性能状态超过该值时则失效，通常Ls为预先给定值。

通过利用非齐次Poisson分布强度函数随时间变化的性质，可以较好地反映出维护不改变装备失效速度的特点。同时，结合上述假设，可以得到定期维护装备任意时刻点的性能状态变化规律，为制定其维修策略奠定了基础。

2 军械装备维修策略研究

不等检测间隔可以有效地降低装备的维修费用，采用不等间隔的维护与预防性维修相结合的方式研究军械装备的维修策略，具体如下：

1）装备在时间（0,tn］内正常工作时，只对其进行维护行为，不采取其他维修行为。记维护时刻为t1,t2…tn，每次维护后只恢复装备的性能状态，装备保持原有的失效速度继续工作到下一维护时刻。

2）当装备在tn时刻进行最后一次维修后，继续工作到te时刻后进行预防性维修将装备修复如新。

3）装备一旦故障停机，则会立即进行事后维修将装备修复如新。

2.2.1 维修策略模型建立

1）工作时间分析。

根据本文所提出的维修策略，应对装备的维护时刻t1,t2,…,tn和预防性维修时刻te进行确定。为了方便求解，根据维修行为分为2个阶段进行求解：①维护阶段；②维修阶段。

当装备处于维护阶段，其工作时间为（0,tn］。记装备寿命的密度函数为f(t)，由式（6）进行确定。当故障发生在（0,t1］的情况下，其平均工作时间为

当故障发生在（t1,t2］的情况下，装备等价于在（0,t1］没有发生故障，其平均工作时间为

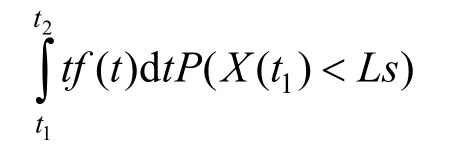
依次递推，当故障发生在（tn-1,tn］的情况下，装备等价于在（0,tn-1］没有发生故障，其平均工作时间为

综上所述，可以得到装备在维护阶段的平均工作时间为

当装备处于维修阶段时，装备的工作时间段为(tn,te]。在装备维护阶段没有发生故障的情况下，可以得到装备维修阶段的平均工作时间为

只有当装备维护阶段不发生故障时，装备才能处于维修阶段，所以装备维修阶段的平均工作时间与装备维护阶段的故障情况有关。记装备在维护阶段不发生故障概率为P′，则其应满足下式：

上式表明在各维护时刻到来之前，装备没有发生故障。

那么，装备在维修阶段的实际平均工作时间应为

综上所述，装备寿命周期内的平均工作时间为

2）费用分析。

定期维护装备的维修费用相关量为维护费用Cs、预防性维修费用Cm和事后维修费用Cf，三者关系满足Cs＜Cm＜Cf。其中维护费用与装备的维护次数相关，预防性维修费用与装备的维护次数、工作时间长度有关，事后维修费用与装备的故障概率有关。因此，定期维护装备的维护次数和工作时间长度是影响其维修费用的主要因素。

根据更新理论，定期维护装备长时间工作的维修费用率为

其中，E(C)为寿命周期内的平均维修费用。

当定期维护装备在维护阶段，其工作时间段为（0,tn］。考虑装备各维护点的维修费用，如果故障发生在（0,t1］时，装备平均维修费用为

如果故障发生在（t1,t2］时，装备平均维修费用为

依次递推，当故障发生在（tn-1,tn］时，装备平均维修费用为

综上所述，可以得到装备在维护阶段的平均维修费用为

当装备在维修阶段，其工作时间段为(tn,te)。显然，该阶段的平均维修费用与维护阶段装备不发生故障的概率有关，综合考虑得到：

综上所述，得到定期维护装备寿命周期的平均维修费用为

3）维修优化模型。

对于定期维护装备而言，为了能够提高装备完成任务的能力，需要确保其具备较高的连续工作能力，但是随着工作时间的延长需要进行维护以避免装备故障停机。而装备寿命周期内维护过于频繁不仅会增加维修成本，也会降低连续工作能力。因此，本文从提高装备完成任务的能力和平均维修费用率2个方面对定期维护装备的维修策略进行优化。

为了确保装备具备较高的任务成功性，一般可以通过避免装备在执行任务期间发生故障来实现。为此外国学者Kumar定义了装备完成任务的能力-生存概率[12]满足：

式中：t为装备连续工作时间；ts为任务持续时间；α为使用方承担的生存风险。

对于定期维护装备而言，为了保证其具备较高的任务成功性，维护时刻t1,t2,…,tn应满足生存概率的条件。对于任意的i=1,2,…n，应满足：

由于维护并不改变装备的失效速度，所以随着时间的延长其失效速度越来越快，这就导致了装备相邻维护的间隔时间Δti=ti-ti-1将会逐渐缩短。当间隔时间Δti＜ts，则说明装备在执行任务期间需要进行一次维护，与保证装备连续工作完成任务的初衷相悖。此时，维护时刻ti-1为最后1次维护时刻，记为tn。定期维护装备转入维修阶段。

在维修阶段，单纯的维护已经无法保证装备满足生存概率的条件。此时，为了避免定期维护装备在使用过程（不特指任务持续期间）中出现故障，造成较高的维修费用，需要确定合适的预防性维修时间te(＞tn)将其状态恢复到全新状态，即修复如新。

根据上文分析，本文以维护时刻ti(i=1,2,…,n)和预防性维修时刻te为优化变量，以装备完成任务的生存概率为约束，装备平均维修费用率最小为目标，建立定期维护装备的维修策略优化模型如下：

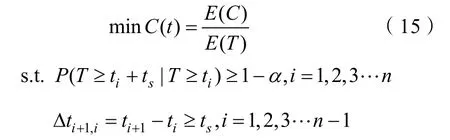
2.2.2 实例分析

如果某装备能够通过维护恢复其状态（即退化量），便可以利用本文方法研究其定期维护策略。某水中兵器用电池的平均寿命为14 005次充放电，其寿命分布函数满足：

式中：Ls=2.8；μt=1.4744×10-8t2；σt=7.3796×10-5t；t为装备的充放电次数。

假设每次维护费用Cs=200元，预防性维修费用Cm=10 000元，更换维修费用Cf=80 000元。并假定装备的免维护期ts=1 000次，使用方所承担的风险α=0.2。

利用本文方法可以得到该装备的维修策略如表1。

表1 维修策略Table 1 Maintenance strategy

其中，第 14次时刻为装备的维修时刻，装备进行预防性维修，至此装备的1个寿命周期结束。采用该维护策略，装备平均维修费用率为0.347 2元/次。

研究该装备平均维修费用率随计划性维修对应的充放电次数的变化规律，可得到图3。

图3 平均维修费用率随充电次数变化规律图Fig.3 Diagram of average maintenance cost rate variation with charging times

由图3可知，随着计划性维修对应的充放电次数的增加，平均维修费用率呈现出先降后增的变化趋势。虽然预防性维修时间越早，装备故障概率越低，但是并没有充分发挥其剩余寿命，导致装备平均维修费用率会随着充放电次数增加而下降。相反，如果预防性维修时间较晚，则会导致装备故障停机，使用方不得不支付高额的事后维修费用，所以导致装备平均维修费用率又会随着充放电次数增加而上升。由上述分析可知，优化目标与变量之间的关系曲线上必定存在一个点，能够令平均维修费用率达到最小。该现象不仅与实际情况相符，也与计算结果一致，说明求解结果较为合理。

在不考虑维修行为参与的情况下，装备的平均寿命仅为14 005次，而通过表1可以发现该维修策略有效地延长了装备的使用寿命。进一步考虑，如果不考虑维护，仅对装备状态进行检测，可以得到该装备视情维修策略下的平均维修费用率为0.913 2元/次。该结果针对于无法维护的装备而言比较合适，但是注意到该结果要大于本文策略下的平均维修费用率0.347 2元/次。这是因为定期检测策略侧重于对状态的检测，当状态超过规定值才采取维修行为（即装备的1个使用周期内只有1次维修行为），所以装备的寿命周期相对于本文策略而言较短，进而导致费用率较高。由此可见，本文的维修策略不仅可以延长使用寿命，而且从经济角度来看该策略更利于降低维修成本，说明了该策略的合理性。

3 结束语

本文分析了维护对军械装备可靠性规律的影响，利用退化强度函数从性能退化速度角度描述了装备的性能退化规律。提出了维护与预防性维修相结合的维修策略，建立了相应的维修策略优化模型，并开展了数值分析。通过算例分析，说明该策略能够有效延长装备的工作时间，并减少全寿命周期内的维修费用。