基于凸优化理论的可扫描稀疏阵列综合

孔 玥, 邱明华,黄 晟, 祁峥东 ,陈 浩

(1.中国船舶集团有限公司第八研究院，南京 211153 ； 2.安徽师范大学 物理与电子信息学院，安徽 芜湖 241002)

0 引 言

阵列天线方向图综合的研究内容是把若干个天线单元按照一定的组合布阵方式进行排列和激励，利用电磁波的叠加和干涉机制，将天线阵列中多个相干单元的辐射电磁波在空间相互干涉并叠加，使得电磁辐射在某些空间区域得以加强，而在其他一些空间区域减弱，使得不变的总辐射能量在空间重新分布以产生特殊的辐射性能指标，以实现理想的方向图。与单个天线相比，阵列天线综合的优势即在于可以实现特殊的方向图，例如可扫描波束、复杂波束形成(较强的方向性、窄波束、高增益)等。综上所述，各种类型的阵列天线在电子对抗、无线通信和雷达声呐等领域拥有极为广泛的应用前景。[1-2]

随着军用和民用领域对无线通信系统和雷达声呐的灵敏度、分辨率等性能指标要求不断提升，使得阵列天线的规模向着超大型、巨型阵列发展。与此同时，稀疏阵的布置可以有效减少天线单元(通道)的总数，从而降低馈电网络的复杂度，以降低系统的造价。因此，关于稀疏阵设计的研究受到了越来越多学者的关注[3-4]。然而，稀疏阵列综合中的阵元位置优化属于非线性优化问题，以往寻优需要采用智能优化算法，如粒子群算法(PSO)[5]、遗传算法(GA)[6]、 蚁群优化算法(ACO)[7]和模拟退火法(SA)[8]等。尽管此类全局优化算法在阵列综合领域取得了良好的应用成果，但通常只能适用于阵元单元数量较少的直线阵(平面阵)综合问题。当处理大型阵列综合问题时，这些算法会暴露出运算量激增且陷入局部最优解的缺点，从而导致优化性能明显下降。目前，针对大型稀疏阵列的综合问题是雷达工程领域一个热门的研究方向。

稀疏阵综合的目的是阵列元数最少化，此阵列综合问题属于L0范数最小化问题，即NP困难问题。本文针对以减少阵列单元总数为优化目标的稀布阵综合问题，将网格中阵元均匀离散化分布的阵列等同于一个过采样的虚拟均匀阵。借助压缩感知(Compressed Sensing，简称CS)理论，上述高度非线性阵列优化问题可转化为CS的稀疏信号重建问题，并采用迭代加权的最小化L1范数的凸优化算法求解得出激励幅度及可用阵元位置。

利用相位的规律变化实现方向图在期望空域内扫描是阵列综合领域中一种最基本的应用，通常还需满足副瓣电平的阈值限制要求。以往的文献资料中[9]稀疏阵综合中的低副瓣赋形仅限于法向控制，忽视了远场方向图在扫描状态下峰值副瓣电平急剧恶化的情形。这主要是由于以往算法都只考虑了法向方向图可见区域的综合，而忽略了阵列在扫描状态下不可见区域的高副瓣或栅瓣进入可见区域的情形。

针对可扫描阵列低副瓣综合问题，本文综合区域不限于可见区域，而是将范围扩大至阵列设计要求的俯仰向最大扫描角。将此思想与最大化稀疏阵列综合方法结合，实现了可扫描最大化稀疏阵列低副瓣设计，且本文算例中对扫描范围与稀疏阵的阵元缩减比的关系进行了对比。

此外，本文也讨论了凸优化(Convex programming optimization, CP)方法在平面阵列综合中的应用，提出了一种结合动态控制策略的凸优化算法，将控制主瓣宽度的非凸优化问题转化成凸优化问题进行求解，在天线主瓣不展宽的情况下可以有效降低峰值副瓣电平。仿真实验表明，与传统阵列相比，本文提出的阵列可以用更少的阵元数实现相同角度的波束扫描。

1 算法应用模型

1.1 远场方向图模型

本节假设有2M×2N个各向同性阵列单元均匀分布一个平面上，各阵元等间距排布，沿x轴和y轴阵元间距分别为dx和dy，则其远场方向图可以表示为

(1)

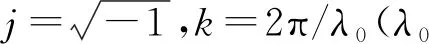
a=[a1，1,a1，2,…,a2M，2N-1,a2M，2N]，

w(u,v)=[ejβ[(-M+1/2)du+(-N+1/2)du]·

ejβ[(-M+1/2)du+(-N+3/2)du],…,

ejβ[(M-1/2)du+(N-3/2)du]·

ejβ[(M-1/2)du+(N-1/2)du]]

综上所述，远场方向图(1)表述为AF=wa。

1.2 凸优化方法

本文将凸优化算法应用于阵列天线方向图综合问题，以期减少阵列中单元数量的同时提高方向图性能，优化问题表述为

(2)

这里，远场方向图|AF|2的主瓣区域(SB)应尽可能地逼近期望波形d(u)，其中d(u)∈R+。|AF|2与d(u)之间的距离ε尽可能地缩小。副瓣部分(SB)的峰值电平应该小于ρ(u)。

从式(2)中可以明显看出，控制主瓣宽度的约束条件为非凸函数。这里对以往凸优化算法进行改进，引入多变量的Multi-Convex算法，通过迭代的多凸模型来近似求解关于控制主瓣宽度的非凸问题，表述如下：

|(wal)Hwar-d|≤ε,al=ar|war|≤ρ

(3)

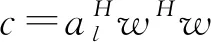
|car-d|≤ε，al=ar

(4)

为快速获得全局最优解，这里利用文献[10-13]中的基于迭代傅里叶算法获得的满足式(2)的激励权值作为本节凸优化算法的初值。

根据文献[10-13]，针对扫描阵列低峰值副瓣综合问题，待综合的区域不能仅限于可见区域，应将综合区域扩大到u2+v2≤r2范围，其中r=1+sinθm。这里θm为阵列扫描过程中需要实现的俯仰向最大扫描角。

1.3 迭代加权L1范数理论

为使阵列尽可能地稀疏,即阵列中单元总数尽可能少，稀疏阵列的优化问题由下式表述:

min‖a‖0

(5)

式(5)表示激励向量或矩阵中非零激励阵元的个数的累加。正是L0范数的这一特点使得其式(5)范数作为稀疏化的度量非常适合。但是，式(5)的L0范数本质上属于NP问题，无论阵列规模大小均难以求解。为解决此问题，这里将式(5)的约束问题松弛变换到维度更高的L1范数最小化问题，函数如下：

min‖a‖1

(6)

本节中，利用重加权L1范数优化算法完成式(5)中L0范数最小化的阵列稀疏化设计目标。在迭代过程中上一步迭代完成的封闭解将作为下一步迭代的初值。结合第1章激励矢量表达式，在第k+1次迭代过程中激励约束表述为

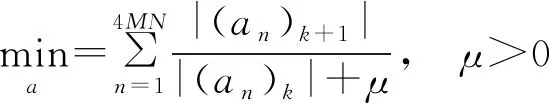
(7)

为防止式(7)在迭代过程中出现分母为零的情况，这里引入参数μ(>0)，则基于凸优化理论的可扫描稀疏阵列综合问题可以表述为

(8)

2 计算实例

为了验证第1章中提出的凸优化算法，本文选择文献[14]中凸优化算法综合得出的图15作为期望方向图。本节所有仿真算例均采用台式计算机，硬件数据如下：处理器为Intel® CoreTMi5-6500T，主频为3.4 GHz，内存为12 GB。仿真软件为MATLAB R2018a。式(8)中μ值选择0.001。

初始阵列选择口径为5λ×5λ的正方形平面阵。假定单元方向图各向同性，且各阵元等间距排布，沿x轴和y轴阵元间距分别为0.5λ和0.5λ。仿真过程中，待综合的区域不仅限于可见区域，而且还将综合区域扩大到51°(与文献[14]中设置相同)。此角度为阵列设计指标中的期望扫描范围上限值。

图1给出了本文算法综合优化后得到的三维远场方向图。

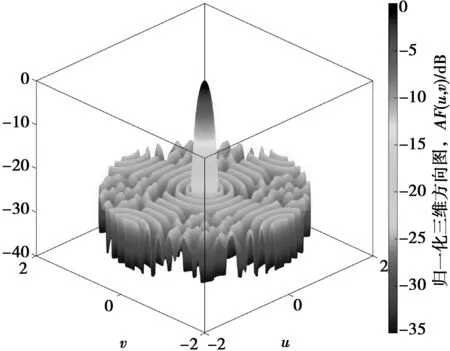
图1 法向三维方向图

值得注意的是，图中已将副瓣区域扩大至不可见区域，显示了u2+v2≤[1+sin(51°)]2范围内的方向图。方向图的峰值副瓣电平为-24.39 dB，与文献[14]中的峰值副瓣电平一致。图2给出了归一化u方向和v方向切面图。

综合后得出的稀疏阵的阵元激励幅度和分布如图3所示。

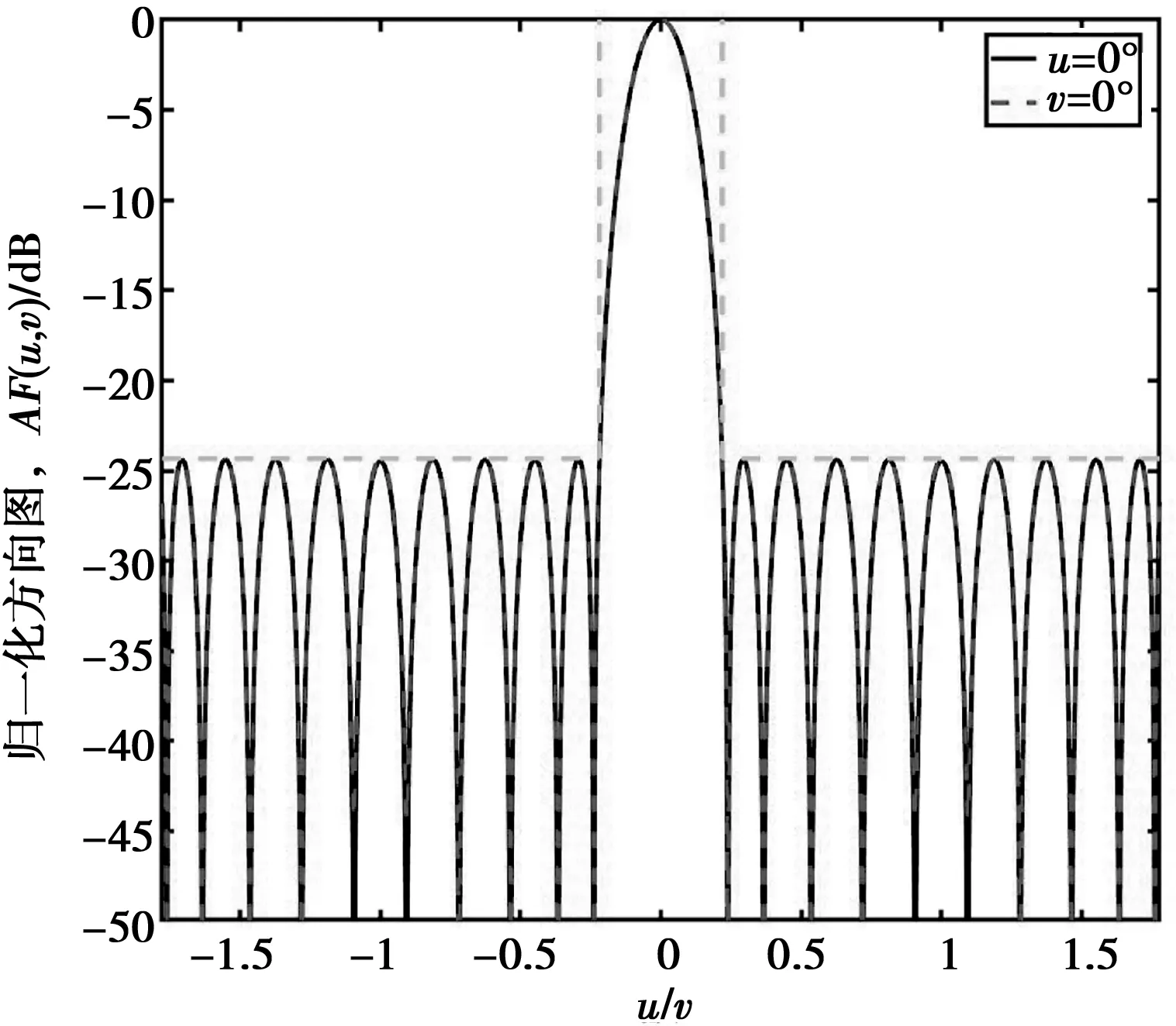
图2 归一化u/v切面远场方向图

图3 105个单元非对称稀疏阵的 阵元位置与激励幅度

如图3中的阵元激励幅度和位置所示，稀疏阵中的阵元总数(The Number of Active Elements,简称Ne)仅为105，实现了13.22%的阵元缩减比(Element Number Reduction Ratio(ENRR),其中有ENRR=1-Ne/(M×N))。与文献[14]中综合得出的满阵(Ne=121)相比，本文的设计结果节省了16 个阵元。

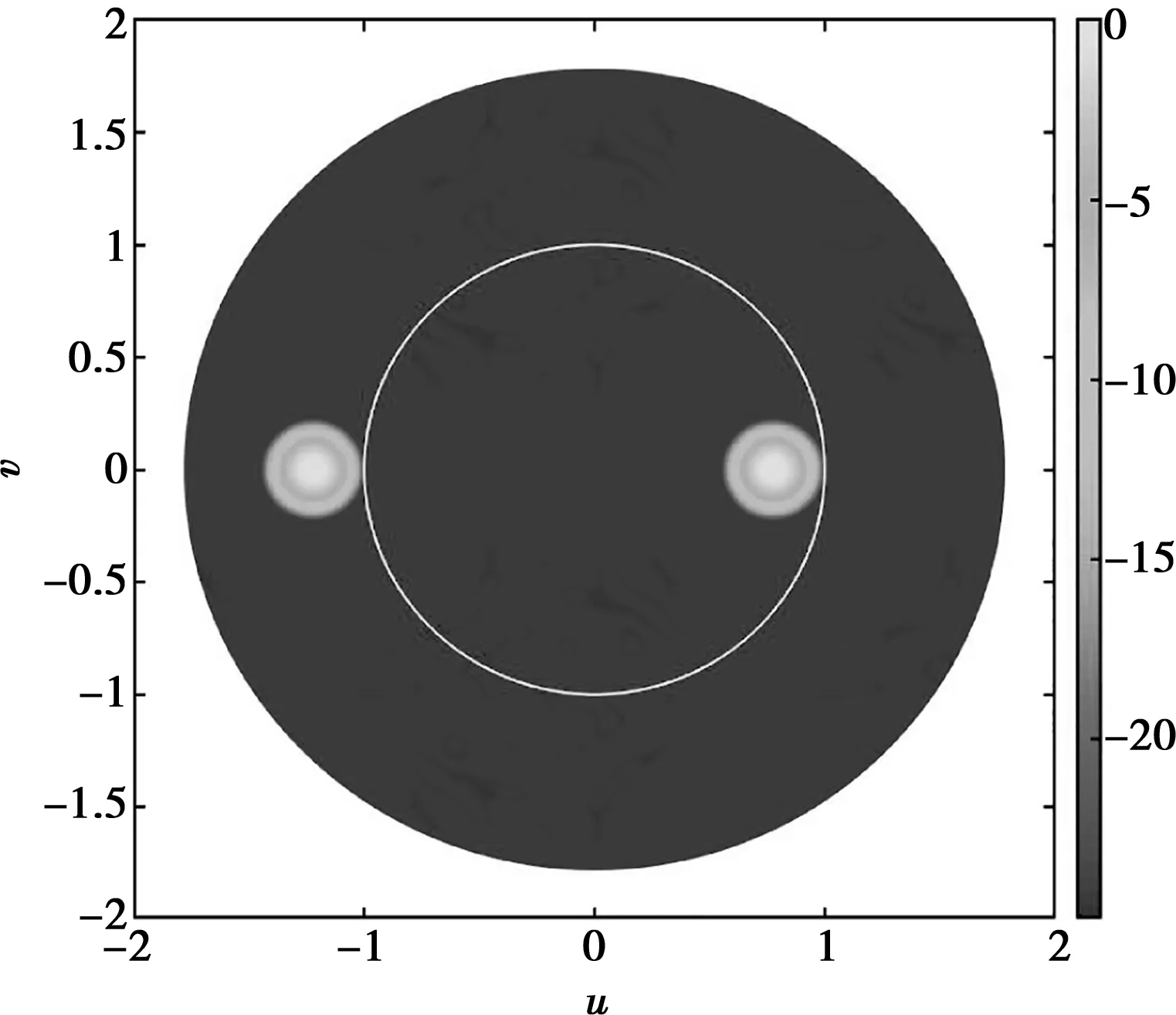
图4 三维方向图的二维投影(主波束 指向(θ, φ)=(51°,0°))

由图4中可以明显得出，当阵列扫描角度达到51°时副瓣电平始终低于阈值，为-24.39 dB，即没有高副瓣进入可见区域。

图5和表1为本章算法综合得出的低副瓣扫描稀疏阵中扫描范围、阵列孔径以及ENRR这3个性能指标之间的关系。

图5 扫描范围与ENRR的对应关系(对应表1)

表1 低副瓣扫描稀疏阵中最大扫描角度和阵元总数两者的对应关系

由图5和表1中方向图辐射性参数和天线口径数据可以得出结论，ENRR随着扫描角度的不断增加而逐渐减小，即表示随着扫描角的增加需要更多的天线单元来实现峰值副瓣电平的抑制。针对孔径为25λ2的平面阵列，本文算法得出的稀疏优化空间的扫描角度极限为51°。在相同峰值副瓣电平阈值、主瓣宽度约束条件下阵元数、阵列孔径如表1内容所示。

3 结束语

本文提出了一种基于迭代算法的可扫描稀疏阵综合方法。该方法包含凸优化算法，即将控制主瓣宽度的非凸优化问题转化成凸约束问题，并结合压缩感知理论，将构建理想辐射性能方向图的具有周期结构的稀疏阵列综合问题转化为迭代加权L1范数最小化的稀疏重构问题。收敛过程中将本次迭代获得的激励权值闭式解作为下次迭代的初值，由完成迭代过程后获得的激励向量中的非零解来确定激励权值以及可用阵元位置。与参考文献中的算法相比,本文算法在方向图主瓣不展宽的情况下可以实现扫描最大化稀疏阵列低副瓣设计。