基于最小二乘偏差补偿法的舵机模型参数辨识

*唐小军，贺 雯

（井冈山大学数理学院，江西，吉安343009）

0 引言

电动舵机作为某型无人旋翼机一个重要的执行机构，控制着旋翼机飞行姿态与轨迹的改变，舵机性能的设计将直接影响着旋翼机动态性能[1-3]。为对舵机性能进行全面分析，需建立舵机的数学模型，可从舵机机理方面分析系统的模型，采用辨识方法去辨识模型参数[4-5]。

系统辨识在1962年由Zadeh 提出[6]，国内外对舵机模型的参数辨识研究较多，通常采用最小二乘法、最大似然法、相关函数法以及基于人工智能的辨识方法等不同的优化方法等[7-11]。在实际的舵机辨识中，关注更多的是舵机系统模型的良好估计，而对噪声模型基本不用关注，偏差补偿法是一种有效获得模型参数的方法。

本文针对舵机特点，对电机、减速器、传动等部件进行逐级建模，先建立舵机各组件的数学模型，进行整体综合后，得到舵机的整个系统模型[12]。在此基础上，采用最小二乘偏差补偿法辨识模型参数，为舵机的性能分析及设计提供基础。

1 机理模型建立

1.1 建立电机与负载的模型

在伺服舵机中，一般都是采用直流电机直接连接负载的方式，从而可以产生较大转矩，带动负载运动，具有方便控制、线性度好的优点。一般在高精度控制系统中，驱动电机都是选用直流电机。可对电机与负载进行简化后，得到其等效电路图(图1)：

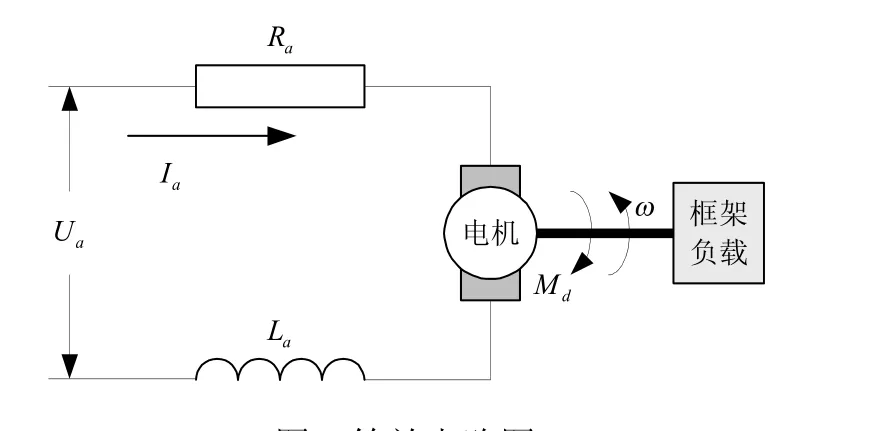
图1 等效电路图Fig.1 Equivalent circuit diagram

在图1中，aU表示电压的平均值，aR表示等效电阻，aI表示电流，aM为干扰力矩，ω表示角速度，aL为等效电感。

在直流力矩电机中，由电压平衡方程得到：

在初始条件下，将前四式进行拉普拉斯变换并进一步整理得：

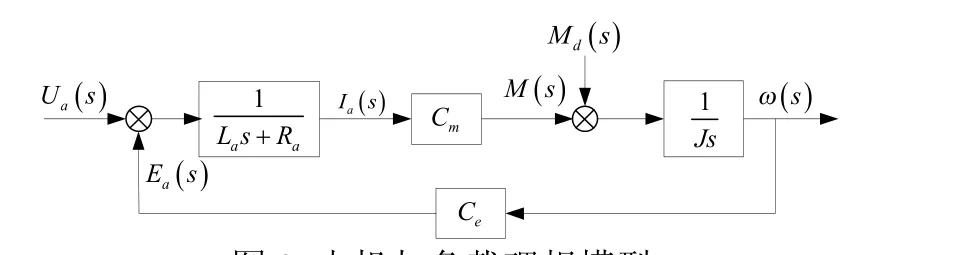
图2 电机与负载理想模型Fig. 2 Ideal model of mortor and load

1.2 建立功放的数学模型

功率放大器（英文名PWM）简称功放，在输入电压转换为一个方波信号后，经功放的放大作用，变成整流电压。在理想状态下，一般来说，整流电压的均值与控制电压是成正比的，其中比例系数pwmK。PWM 同时具有延迟与放大作用，其数学表达式为：

1.3 建立减速器的数学模型

电机转动，输出的是角度位移θ，在经过减速装置后，产生减速作用，借助传动机构，转换成线位移信号l，在忽略其他因素的影响，可以得到线位移与角位移关系式：

1.4 建立电位器的模型

在舵机中，作为控制回路的反馈元件，电位器所起的作用是将信号与输入电压之间的误差进行比较，使舵机工作在指定位置。它的数学模型为一个比列环节，可表示为：

1.5 建立伺服舵机整体的系统模型

对上述电机与负载、功放、减速器、电位器等五个部件组件进行研究讨论，并建立对应的数学模型，根据结构原理，得到伺服舵机模型（图3）。

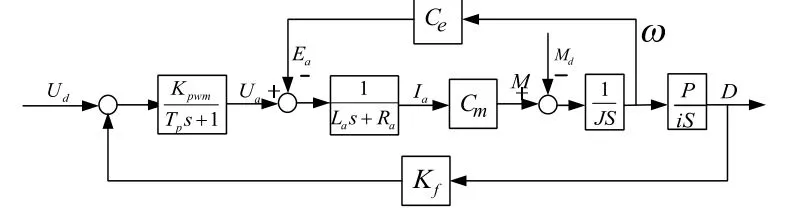
图3 机理模型Fig.3 Mechanism model

2 舵机模型中的参数辨识

舵机作为一个执行机构，对旋翼机进行姿态和轨迹控制时，要求舵机系统具有一个较精确的数学模型，但是，舵机控制回路相对复杂，模型参数有时难以确定，在此情形下，可通过系统辨识方法去确定舵机数学模型中的参数。

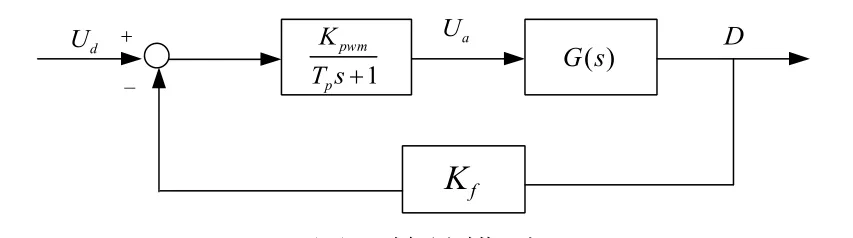
图4 等效模型Fig.4 Equivalent model

将图3 中伺服舵机的机理模型进行等效得到等效模型（图4）：在图4中的前馈控制器中，惯性环节中参数pT由于小到基本忽略不计，由此，得到简化模型图5：

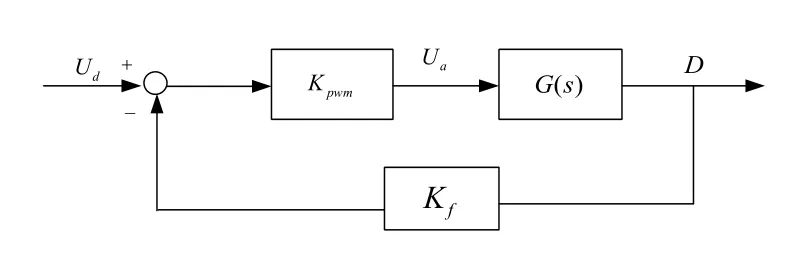
图5 简化模型Fig. 5 Simplified model

在图5中，设闭环系统传递函数为( )sφ，得到如下关系式：

3 试验仿真

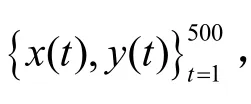
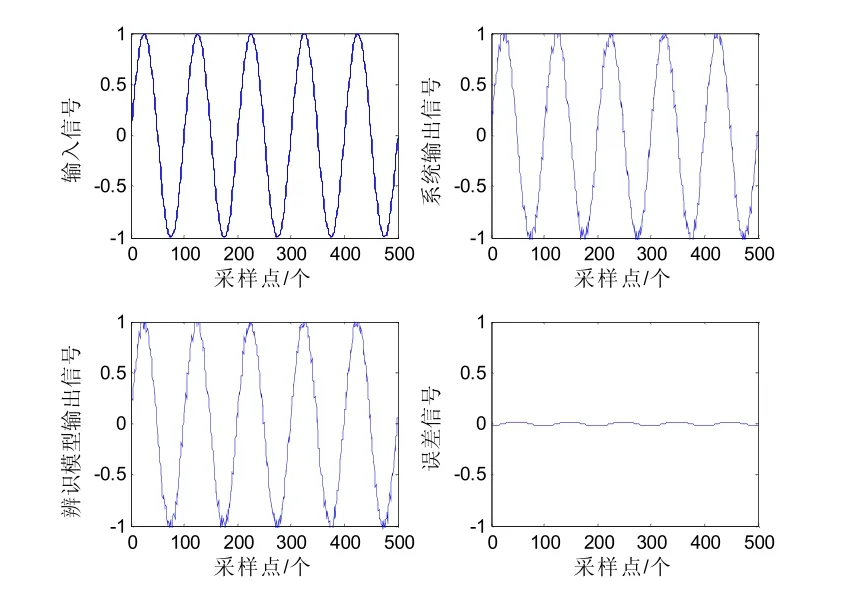
图6 基于正弦波输入的模型验证Fig.6 Model verification based on sin wave

在图6 中显示，真实系统输出与辨识系统输出之间误差为一白噪声。为进一步验证所提辨识方法的精确与有效性，继续采用阶跃信号进行输入，对模型进行验证并与采用最小二乘法辨识结果进行比较如下图7：

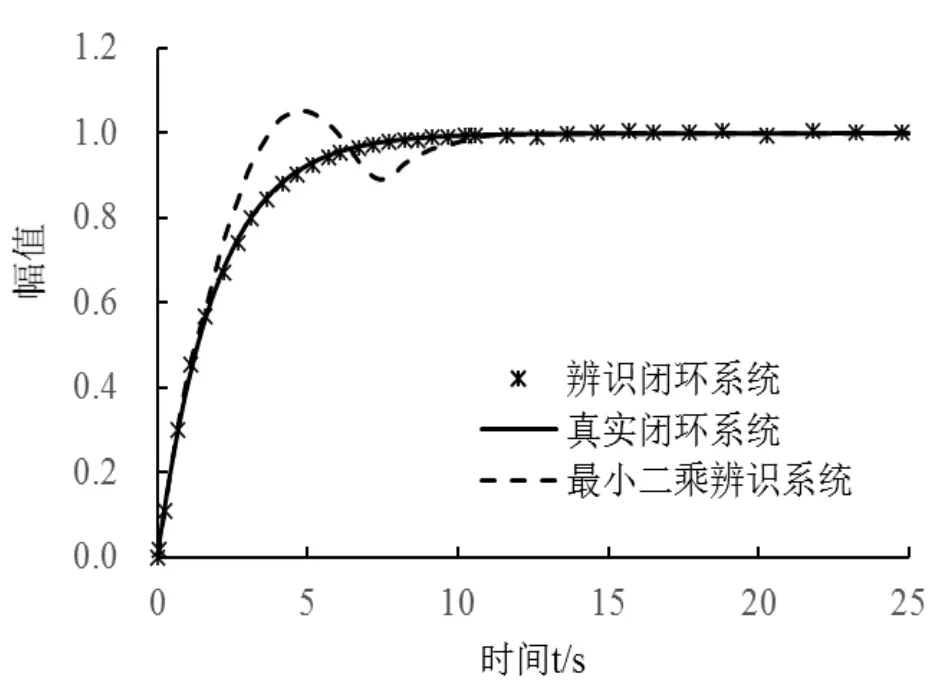
图7 基于阶跃的模型验证Fig.7 Model verification based on step

图7结果显示，与最小二乘法辨识模型相比，采用文中所提方法辨识模型与舵机系统模型之间阶跃响应曲线紧密吻合，具有更高辨识精度。

4 小结

作为无人旋翼机中关键的随动装置，舵机性能的设计对旋翼机机动性能起着决定性作用。论文在对舵机进行机理分析之后，采用最小二乘偏差补偿法去辨识舵机系统模型参数。通过试验仿真，基于正弦波与阶跃信号输入的仿真实验中，真实系统模型与辨识模型的信号输出曲线具有较高吻合度，说明该方法具有较高辨识精度。