基于信息熵的自适应高斯金字塔的LSD算法改进
2020-12-24王冬梅
王冬梅, 谢 鑫
(东北石油大学 电气信息工程学院, 黑龙江 大庆 163318)
0 引 言
线段作为图像的低阶特征, 常用于分析图像。算法检测出的线段需要保留原图像中物体完整的轮廓信息, 又需要抛弃没有利用价值的背景。围绕该问题, 近年来人们提出了众多线段检测算法。主流线段检测算法有基于像素梯度幅值的算法和基于像素梯度角度的算法。
Akinlar等[1]提出了EDLines(Real-time Line Segment Detector)算法, 这是一种基于像素梯度幅值的算法, 他能快速检测一张图像中的线段信息, 并能实现实时给出结果, 适合应用于实时系统。然而由于EDLines算法本身检测线段的机制, 导致其在检测较长的连续边缘或交叉边缘时容易出现不连续的问题。Gioi等[2]提出了LSD(Line Segment Detector)算法, 该算法在聚类类似梯度角度的像素点时, 由于仅通过一个像素点的八连通区域判断周围是否有类似梯度角度的像素点, 容易产生不连续的线段。这种线段不连续的问题在分辨率高的图像或受到噪声干扰的图像中表现的更加明显。为解决LSD算法在提取线段时容易产生线段不连续的问题, 郭克友等[3]提出了一种LSD改进算法, 该算法首先采用LDA(Linear Discriminant Analysis)对道路图像进行有针对性的灰度化; 其次再用LSD算法检测灰度图像中的直线部分。刘璧钺等[4]提出了一种LSD改进算法, 解决原LSD算法在检测被遮挡或局部模糊的边缘时, 将原本连续的边缘分割成多条短线的问题, 但效果并不理想。
针对原LSD算法在对图像提取线段时常常出现线段不连续的问题, 笔者提出一种LSD改进算法。该算法首先通过计算处理后的图像与原图之间的互信息熵, 确定高斯金字塔的层数与层内图像数量; 其次使用改进的大津阈值, 根据图像的梯度峰值将图像分割成不同区域并计算相应梯度阈值, 分离出图像背景; 最后根据梯度角度寻找线段, 并通过赫尔姆霍兹准则验证线段。
通过一组具有代表性的图像, 与比较流行的Hough变换(Hough Transform)[5]、 PPHT(Progressive Probabilistic Hough Transform)[6]、 LSWMS(Line Segment detection using Weighted Mean Shift)[7]、 LSD、 EDLines算法进行了比较, 用结果图像进行定性分析, 并且用线段数量、 总长度及平均长度定量分析各个算法的性能。最后进行抗噪声实验。
1 核心算法
1.1 LSD算法原理
LSD算法[1]是一种基于梯度角度的算法。该算法首先将输入图像转换为灰度图并求取像素的梯度幅值, 对像素梯度幅值进行从大到小排序; 其次由于梯度幅值相对较大的像素点周围更可能出现边缘, 因此以梯度幅值相对较大的像素点作为种子点, 聚类类似梯度角度的像素点形成线段区域; 再次通过计算能包括整个线段区域的最小矩形, 确定线段的位置、 长度和角度等信息; 最终该算法采用赫尔姆霍兹准则验证线段是否存在于实际图像中。
1.2 一种基于信息熵的自适应高斯金字塔算法
高斯金字塔实现在不同的尺度对同一个物体观察, 挖掘同一物体在不同尺度下的图像信息, 使算法提取出的信息更加完整[8-9]。现有多数文章报道的高斯金字塔的层数与层内图像数量均是固定的。在构建图像金字塔过程中, 会对图像进行降采样和高斯模糊。若对图像进行多次降采样或高斯模糊, 图像中原本独立的物体可能会连在一起, 造成图像失真。若算法对失真图像进行线段检测, 最终检测结果中必然带有不正确的线段信息, 已经失真的图像在高斯金字塔中是毫无作用的。高斯金字塔中图像数量并不是越多越好, 但高斯金字塔中图像过少时, 会导致高斯金字塔丢失某个尺度的信息, 最终检测结果中可能会丢失重要线段信息。
因此高斯金字塔的组数与每组组内图像数量的确定方式显得尤为重要, 笔者提出基于信息熵的自适应高斯金字塔。归一化信息熵可以描述两张图像之间的相似程度[10], 借助这一特性, 将高斯模糊或降采样后的图像与原图像进行计算归一化信息熵, 算法将计算结果与阈值进行比较, 决定是否保留处理后的图像, 从而构建出自适应高斯金字塔。实现根据输入图像的不同而建立不同的高斯金字塔。使算法能适应各种各样的图像。
归一化信息熵的计算公式如下
其中A,B为两张图像,H(A)、H(B)为图像信息熵,H(A,B)为联合信息熵,NNMI(A,B)为互信息熵。
算法将阈值ε0,ε1,…,εo和阈值α作为参数。阈值α决定了自适应高斯金字塔具体构建多少组, 阈值ε0,ε1,…,εo分别决定了自适应高斯金字塔对应组组内有多少张图像, 参数具体设定方式在实验中论述。算法对图像构建自适应高斯金字塔的具体步骤如下。
Step1 设定变量o为自适应高斯金字塔的组序号, 变量i为自适应高斯金字塔组内图像序号, 并初始化o、i为0。
Step2 将输入图像作为自适应高斯金字塔的第o组第i张图像, 即金字塔最底层的图像。
Step3 对自适应高斯金字塔的第o组第i张图像进行高斯模糊, 并计算模糊后的图像与输入图像之间的归一化信息熵。判断归一化信息熵是否小于阈值εo。若小于阈值, 则i=i+1, 且将模糊后的图像存入自适应高斯金字塔第o组第i张的位置; 若大于阈值, 则抛弃当前图像, 并停止构建当前组图像。
Step4 对自适应高斯金字塔中第o组第i张图像进行降采样, 计算降采样后的图像与输入图像之间的归一化信息熵。判断归一化信息熵是否小于阈值α。若小于阈值, 则o=o+1, 且将图像存入自适应高斯金字塔第o组第i张的位置, 并重复Step3~Step4; 若大于阈值, 则抛弃当前图像, 并停止构建自适应高斯金字塔。
Step5 得到输入图像对应的金字塔。
通过计算图像归一化互信息熵的方式确定自适应高斯金字塔的组数以及每组组内图像数量。自适应高斯金字塔的结构如图1所示。对输入图像, 算法为其构建的高斯金字塔中共有o+1组, 并且每组组内图像数量是不定的, 分别为i0+1,i1+1,i2+1,…,io+1张; 组内的图像是由当前组的前一张图像高斯模糊得到的; 下一组的第1张图像是前一组最后一张图像降采样得到的。
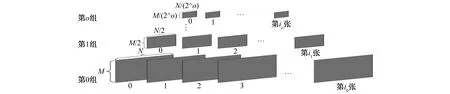
图1 自适应高斯金字塔的结构图
1.3 大津阈值原理
大津阈值是一种图像分割的算法。该算法首先将图像灰度化并统计每个灰度级在图像中出现的个数; 其次计算每个灰度级在图像中所占比例; 最后遍历所有灰度级, 找出能使前景和背景的类间方差最大的灰度级, 即得到该图像前景和背景的分割阈值[11-15]
g=w0w1(u0-u1)2
(5)
其中w0为前景像素点数与图像总像素点数的比例,u0为前景像素点平均灰度,w1为背景像素点数与图像总像素点数的比例,u1为背景像素点平均灰度。
1.4 一种改进的大津阈值
每张图像中都包括前景与背景, 背景对前景中物体的轮廓或边缘并不重要, 并且在背景中可能包含一定的噪声。因此在对图像进行线段检测前, 将前景与背景分离显得尤为重要。这样不仅可以避免算法对一些非边缘像素点进行遍历, 节省算法执行时间; 也能减少噪声干扰, 避免算法对线段的错误判断。因为图像的不同, 所以图像对应的梯度阈值也应该是不同的。
原大津阈值算法是对整张图像计算出一个阈值, 通过其值实现对图像的分割。当图像中的背景像素值类似时, 原大津阈值算法分割图像能发挥出比较好的效果。然而并不是每张图像的背景像素值都是类似的。大部分图像中的背景像素值有几类, 原大津阈值算法就不能很好地将前景与背景分离, 并且很可能将前景部分像素认作是背景像素。
因此笔者提出改进的大津阈值算法: 首先根据图像像素梯度幅值, 将图像分割成若干个局部; 其次计算出每个图像局部的梯度阈值; 再次通过梯度阈值将前景与背景分离, 抛弃背景像素对应的梯度; 最终实现图像的前景与背景实现精确分离, 从而抑制背景噪声的影响。
改进的大津阈值算法的具体步骤如下。
Step1 读取图像金字塔中的一张图像, 并对整张图像像素求取梯度。
Step2 找出局部梯度峰值的像素点, 将这些像素点的笛卡尔坐标转换为极坐标, 统计出共线的像素点, 通过最小二乘方法拟合线段; 计算出所得线段之间的交点, 通过线段交点即可将图像分割成若干局部。
Step3 分别对图像的每个局部计算出一个梯度阈值。
Step4 通过局部的梯度阈值将图像局部的前景与背景分离, 抛弃背景像素对应的梯度。
Step5 判断当前读取的图像是否为金字塔中的最后一张图像, 若不是则重复Step1~Step5; 若是则结束算法。
Step6 得到金字塔中图像前景像素对应的梯度。
流程图如图2所示。

图2 改进的大津阈值算法的流程图
2 仿真实验
笔者实验操作平台电脑: 处理器为AMD Ryzen 5 2600X、 内存为8 GByte、 操作系统为Windows 10。笔者所提算法(MultiscaleLSD)和做对比的算法均在Visual Studio平台上用C++实现。
利用YorkUrbanDB(YorkUrban Dataset)数据库[16]中的图像对算法进行效果比较和抗噪声实验, 实验涉及的算法有: Hough变换(Hough Transform)、 PPHT、 LSWMS、 LSD、 EDLines。其中Hough、 PPHT算法从Opencv 2.4.11软件库中调用, LSWMS、 LSD、 EDLines算法由笔者提供。
2.1 算法参数
该算法继承了原LSD算法无参输入的优点, 因此阈值的设定应根据输入图像的不同而不同。参数的设定如下: 阈值α设定为自适应高斯金字塔第0组第0张图像与第1组第0张图像之间归一化信息熵的x倍; 阈值ε0,ε1,…,εo分别设定为对应组的第0张图像与高斯金字塔第0组第0张图像之间归一化信息熵的y倍, 具体x和y值的大小通过实验确定。
实验结果如图3所示, 图3a和图3e分别用于确定y值和x值的实验输入图像; 在还没有确定x值的情况下, 暂且将x设定为0.8, 在同一输入图像的条件下, 将y值分别设定为0.5,0.7,0.9, 其检测结果分别如图3b、 图3c、 图3d所示, 3幅图中差异较大的部分用圆角矩形圈出。图3d相对于图3c, 在墙壁边缘处检测出的细节更少。这是由于将y值设定过大后, 导致输入图像对应的高斯金字塔组内图像数量过少, 算法无法将图像中的线段信息完整检测出, 使检测结果丢失部分线段信息。图3b相对于图3c, 虽然在墙壁边缘处检测出的细节差不多, 但在地面和树木的位置中出现了更多的短线段, 这些短线段是多余的。这是由于将y值设定过小后, 导致输入图像对应的高斯金字塔组内图像数量过多, 算法将图像中一些不重要的细节也检测出来。根据以上分析, 为了使算法能尽可能地检测出图像中重要的线段信息, 并且忽略掉图像中背景, 因此该算法将y值设定为0.7。
在确定y值后, 在同一输入图像的条件下, 将x值分别设定为0.4、0.6、0.8, 其检测结果分别如图3f、 图3g、 图3h所示, 3幅图中差异较大的部分用圆角矩形圈出。图3h相对于图3g, 窗户的轮廓细节更少, 这是由于在对输入图像建立的图金字塔组数太少, 导致算法无法将图像中物体的轮廓信息完整检测出。图3f相对于图3g, 虽然窗户的轮廓细节差不多, 但在建筑墙壁上检测出了更多的短线段, 这些线段信息在实际利用中并不能发挥作用。这是由于在对输入图像建立的图金字塔组数太多, 有些组内图像和输入图像相比出现失真, 导致检测出较多短线段。根据以上分析, 因此该算法将x值设定为0.6。
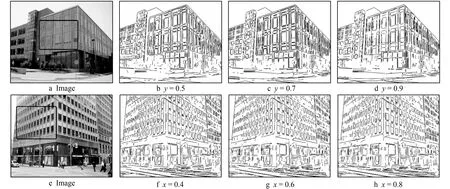
图3 参数选定实验结果
综上所述: 阈值α设定为自适应高斯金字塔第0组第0张图像与第1组第0张图像之间归一化信息熵的0.6倍; 阈值ε0,ε1,…,εo分别设定为对应组的第0张图像与高斯金字塔第0组第0张图像之间归一化信息熵的0.7倍。该参数设置能充分发挥高斯金字塔的优点, 并且算法运行前所设定的参数对任何图像都适用。
2.2 算法测评
为检验各算法线段检测的效果, 将用各个算法的输出图像进行定性分析, 设定算法对输入图像检测出的线段总数量为N、 总长度为L、 平均长度为L/N。用线段数量、 总长度及平均长度定量分析各个算法的性能。最后将笔者所提算法进行抗噪声实验。
教室线段检测结果如图4所示, 其中图4a为输入图像, 图4b是人工标定图像。图4c中边缘不连续, 算法效果差, 例如: 桌子、 椅子和窗户。图4d中丢失大量座椅边缘信息。图4e虽然比图4c、 图4d有进步, 但与图4f相比, 还有很多细节描述不够完整, 并带有一些错误线段。图4f相对于图4e座椅细节信息更加完整, 但有些边缘信息不够完整, 例如: 黑板的下边缘。图4g中的物体轮廓大部分都有, 但少了很多物体细节信息, 例如: 椅子和天花板纹路。图4h是笔者所提算法检测结果, 将图4h与图4g比较, 不难发现图4h检测出的细节比较完整, 与其它算法检测结果相比, 图4h检测出的线段更加连续。

图4 教室线段检测结果
表1为图4所对应的表格。从表1可看出, Hough算法检测出的线段数量最多, 线段总长度不大, 且平均长度最小。PPHT算法检测出的线段数量最少, 并且其中一些线段为错误线段, 使线段平均长度最大。LSWMS算法检测出的线段数量相对于Hough变换算法、 PPHT算法更多, 但相对于LSD、 EDLines、 MultiscaleLSD算法还是太少。LSD、 EDLines两个算法的线段总长度和线段平均长度差不多, 但Edlines的线段数量更多一些, 这是因为EDLines算法在检测时将一些在输入图像中连续边缘当作不连续导致的。MultiscaleLSD算法检测出的线段数量和线段总长度是所有算法结果最多的, 线段平均长度和LSD、 EDLines算法结果相差不多。

表1 教室线段信息
大厅线段检测结果如图5所示, 其中图5a为输入图像, 图5b是人工标定图像。图5c中有较多错误线段, 且很多边缘检测不完整, 例如: 玻璃护栏边缘和窗户。图5d与图5b对比, 有些线段位置有所偏离, 有些线段的长度长于人工标定图像中线段的长度。图5e虽然比图5c、 图5d有进步, 但有些线段没有检测出来, 例如: 图像中的门框。图5f中有很多物体的线段细节, 但有些细节不够完整、 连续, 例如: 左侧的柱子、 地板的纹路。图5g中物体轮廓比较完整, 但少了很多物体细节, 例如: 窗户、 地板的纹路。图5h是笔者所提算法检测结果, 相对于其他算法, 细节都更加完整, 例如图像左侧的柱子、 门框。
表2为图5所对应的表格。从表2可看出, Hough算法检测出的线段数量最多, 但线段总长度不大, 且检测结果中出现较多错误线段, 线段平均长度最小。PPHT算法检测出的线段数量最少, 但线段平均长度最大, 这是因为有些线段的长度要长于标定图像中线段的长度。LSWMS算法检测出的线段数量相对于Hough变换算法、 PPHT算法更多, 但相对于LSD、 EDLines、 MultiscaleLSD还是太少。EDLines算法检测出的线段数量、 总长度均要大于LSD算法的检测结果, 但线段平均长度要略小于LSD的数值, 这是因为EDLines算法在检测时将一些在输入图像中连续边缘当作成不连续导致的。MultiscaleLSD算法检测出的线段数量、 总长度和平均长度是所有算法中最好的。
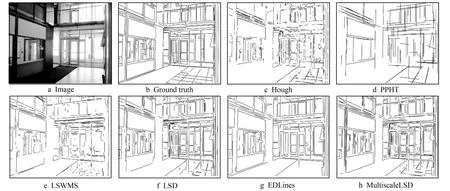
图5 大厅线段检测结果

表2 大厅线段信息
2.3 抗噪声实验
在通常情况下图像受到外界干扰或许会带有一些噪声, 算法在处理这种图像时不能完整检测出图像中的线段信息。为对比不同算法的抗噪声性能, 通过对图像引入一定高斯噪声, 测试在有噪声干扰的情况下算法提取线段的效果。
走廊线段检测结果如图6所示, 图6a为输入图像, 不带有噪声, 图6b是人工标定图像。图6c和图6d检测出图像部分线段, 但是不够完整, 例如: 地板和部分墙体轮廓。图6eLSWMS图像检测出部分地板边缘, 但是带有大量错误线段。图6f和图6g检测出的线段数量差不多, 但是不够完整, 例如: 地板和部分墙体轮廓。图6h是笔者所提算法检测结果, 相对于其他算法, 线段数量更多, 且更加连续。

图6 走廊线段检测结果
走廊线段检测结果(带噪声)如图7所示, 图7a为输入图像, 带有高斯噪声(σ=10), 图7b是人工标定图像。图7c在噪声干扰情况下, 检测出的线段是断断续续的, 且带有较多错误线段。图7d检测的有些线段位置有所偏离。图7e几乎没有检测出较完整的线段, 并带有一些错误线段。图7f和图7g在噪声的干扰下检测出的线段更少。图7h是笔者所提算法检测结果, 相对于其他算法, 线段信息更加丰富。虽然有些线段是断断续续的, 但线段依旧描述出了原图像的边缘信息。

图7 走廊线段检测结果(带噪声)
3 结 语
针对LSD算法提取线段常常出现线段不连续的问题, 笔者提出了一种LSD改进算法。经过图像仿真实验, 验证了该算法能根据输入图像的不同, 建立不同的高斯金字塔, 能充分利用高斯金字塔携带多个尺度的信息; 通过改进的大津阈值算法, 将图像分割成不同区域计算对应的梯度阈值, 将图像的背景和前景进行精确地分离, 减少噪声干扰, 避免算法对线段的错误判断。该算法即解决了LSD原算法缺点又继承了LSD原算法优点, 使提取出的线段更加连续、 完整。通过对图像引入一定噪声, 与其他算法进行比较, 该算法能在噪声干扰的情况下, 仍然能稳定得到满意的结果。
