基于改进标号修正的溃坝逃生路径优化
2020-12-23锁启凤
锁启凤


摘 要: 灾害发生时为确保受灾区居民疏散到安全区,建立疏散路径优化模型。依据溃坝现场情况,以疏散路径最短同时路段通行能力最大为目标建立逃生路径规划模型。考虑到模型是一个多目标优化模型,对标号修正算法的评价准则进行改进以适用于寻找多目标优化模型的最优解集。将该框架应用于龙岩市新罗区,结果表明:在8组方案中,改进的算法找到长度为3741米,路段通行能力评价函数值为2.063的路径最优,充分说明提出算法的優越性,可以为逃生人员规划出可靠的疏散路径。
关键词: 应急疏散;优化问题;逃生;路径规划;标号修正
【中图分类号】F274 【文献标识码】A 【DOI】10.12215/j.issn.1674-3733.2020.40.264
0 引言
洪水,地震等突发性自然灾害事件危及人类的生命安全,面对日益增加的突发事件,人类的防范意识逐渐增强。近些年大部分灾害中依然存在人员伤亡情况。分析原因,灾害发生时灾区居民无法快速了解灾害发展的形势以至于无法得知哪条路径安全。因此,在现有的路况条件下,如果决策者在了解灾害得发展趋势的基础上预先为受灾人群提供一条可以顺利到达安全区域的路径,可以减少伤亡人数。
约束最短路问题是多目标优化问题[1],Stewart和White发现现实世界中许多问题涉及多重,相互冲突的目标,从而首次提出了多目标泛化算法MOA*,处理多目标路径规划问题[2]。大部分文献使用节点扩展方法实现多目标启发式搜索,这样求解的精确度不足,Mandow等人为解决这个问题提出了路径扩展的方法 [3-4]。Dasgupta等人系统地将多准则决策范式推广到启发式搜索领域 [5]。张慧等[6]采用数字高程模型进行地形描述,并通过计算各栅格的坡度、粗糙度、起伏度对地形进行识别,再采用滑动窗及增量式A*算法进行路径规划。
1 问题描述
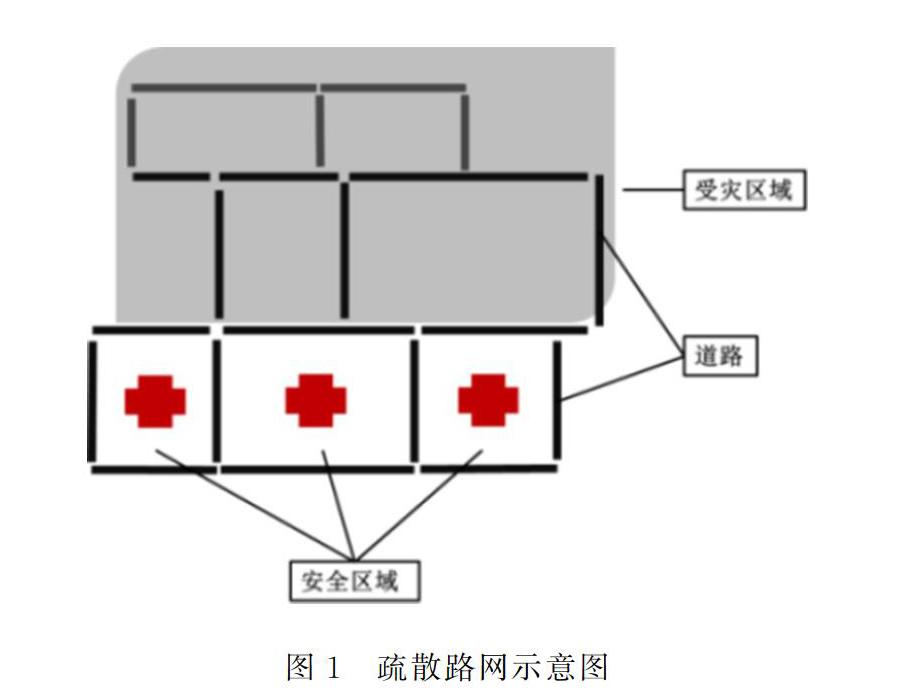
在图1的疏散路网中,灰色区域是受灾区,红色区域是安全区,黑色线段表示路段。假设发生灾难时每个逃生人员都能接收到预警信号,在疏散点到安全点间为逃生人员规划出可靠的疏散路径,确保疏散人员移动到安全区域。根据受灾区域的环境结合路径长度,路段通行能力两个因素规划出一条安全的疏散路径。
多目标优化问题是指在给定约束条件的情况下,目标多于一个并且需要同时极大(小)化这些目标值的问题。一个目标达到最优会使其它目标劣化。因此,多目标优化问题的最优解不止一个,而是存在一个包含多个解的Pareto最优解集合。解决实际的问题时Pareto 最优解集合中解的数量很大不可能逐一求出,况且实际问题只需要一个或几个解,因此需要解决问题者从实际问题出发在Pareto 最优解集合中挑选出一个解作为最终解。
为了更完整描述Pareto最优解,引入两个相关定义[7]:
定义1:令x(x1,x2,…,xn),y(y1,y2,…,yn)为两组解,若x1 定义2:如果x(x1,x2,…,xn)无法被其它解支配,那么x(x1,x2,…,xn)为Pareto最优解。 2 模型建立 定义符号: V:节点集合;A:弧集合;i,j:节点,i,j∈V; O:起点;D:终点; cij=(c(1)ij,c(2)ij),c(1)ij,c(2)ij分别表示路段(i,j)的路径长度和路段通行能力. 2.1 目标函数 mints=∑(i,j∈A)c(1)ijxij+1c(2)ij(1) 式中,ts是影响因素累积成本,c(1)ij是路段(i,j)的长度,c(2)ij是路段(i,j)的通行能力,xij是一个定义如下的二元决策变量: xij∈{0,1},i,j∈A(2) 若选择了路段(i,j),xij=1,否则xij=0. 2.2 约束条件 |∑(i,j)∈Axij-∑(j,i)∈Axji|=1,i∈{O,D} 0,否则.(3) 每个逃生人员有唯一的起点并且选择唯一的终点,公式(3)保证各场景下选择的路径是一段通畅的路径。 2.3 数据准备 本文通过无人机航拍获得研究区域地图数据,如图二(a)的图片格式。通过ArcGIS软件处理,得到如图2(b)所示的点线路网表示,点表示人员聚集的区域或安全区域,线表示路径。路网信息包含路径长度和路段通行能力。路径长度是实际长度值,路段通行能力根据路段宽度以升序的方式生成。路段的长度和宽度皆由ArcGIS软件缓冲得到。根据水源地确定人员逃生的方向,因此相邻两节点间是不可逆的有向路径。 3 算法设计 标号修正算法的思路是[8]:设是G(V,A)一个有向图。首先初始化研究区域路网图中的节点数据和弧长数据,令起点标号为us,对于图中节点集合V中任意一个节点i,赋予两个数值:一个是距离标号ui,存储的信息是起点到该点的累积费用的上界,该费用包括前面提到的路径长度以及路段通行能力。另一个是前趋标号pred[i],记录的是当起点us到该节点i的一条路径的累积费用取到上界时,该条路径中节点i的直接前趋节点。这样,算法通过不断修改这些标号进行迭代计算直到找到终点,此时这些标号不再改变成为永久标号。回溯所有的节点标号可以求出最优路径。基于以上描述,笔者对经典标号修正算法的标号选择准则改进,改进的标号修正算法适用于寻找Pareto最优解,改进的标号修正算法步骤如下: 步骤1:初始化,将两个影响因素的总体费用存储在距离标号集合U中; 步骤2:令起点的距离标号us=0,前趋标号pred(O)=0;对所有其他节点j,令uj为无穷大。 步骤3:若对所有权重为cij的弧(i,j),ujui+cij,算法结束,uj为从起点至节点j的最小总体费用路径,最短路可通过依次寻找前趋标号(pred)获得。 步骤4:寻找满足ui+cijuj的弧(i,j),令uj=ui+cij,pred(j)=i,转至步骤3。 4 实验分析 将框架应用于图2中龙岩市新罗区67个节点99条路径的路网中验证算法的有效性。用ArcGIS软件生成疏散路段的长度(米)以及路段宽度(米)。路段通行能力根据路段宽度在区间[2:12]内以升序的方式生成。 对于节点61-16计算出前8条最优路径,结果如图3所示,图的右上角给出了8次计算得到的路径对应的路径长度累积费用以及路径通行能力累积费用,综合这两个因素,本文算法给出的最优解为第6组解。回溯8条路径得到的可行路径如表1所示: 5 结论 针对溃坝发生水灾时受灾区域人员需要在复杂的环境中转移至安全区域事件,建立逃生路径规划模型。考虑到该问题是一个多目标优化问题,笔者对标号修正算法的评价标准进行改进,改进的算法可以找到Pareto最优解。最后,将该框架应用到龙岩市新罗区示例中,结果表明提出的模型与算法能为灾区居民规划出路径长度最短同时路段通行能力较大的最优路径,可以有效解决应急疏散问题。 参考文献 [1] 王莉.动态不确定路径优化模型与算法[D].北京:北京交通大学,2017.8. [2] Bradley,S,Stewart,et al.Multiobjective A*[J].Journal of the Acm,1991. [3] Dasgupta P,Chakrabarti P P,Desarkar S C.Multiobjective Heuristic Search in AND/OR Graphs[J].Journal of Algorithms,1996,20(2):282-311. [4] L.Mandow and J.L.Pérez de la Cruz.Multicriteria heuristic search[J].European Journal of Operational Research,2003. [5] Harikumar S,Kumar S.Iterative deepening multiobjective A*[M].Elsevier North-Holland,Inc.1996.58(1):11-15. [6] 張慧,荣学文,李贻斌,李彬,丁超,张俊文,张勤.四足机器人地形识别与路径规划算法[J].机器人,2015,37(5): 546-556. [7] 秦玉鑫,张高峰,王裕清.矿灾害环境下多目标路径规划方法[J].控制工程,2017(11):2337-2342. [8] 邢文训,谢金星.现代优化计算方法[M].清华大学出版社,2006.62-77.
