和声搜索算法在坐标转换中的应用

常方敏 李素敏

摘  要： 针对最小二乘算法在处理坐标转换存在准则单一这一问题，本文提出一种思想，将和声搜索算法加入最小二乘坐标转换模型中，从而使传统坐标转换这一P类问题，转换为NP类问题。通过不断迭代使其结果趋近于所设定的函数解，从而实现解的多样性。本文以方向精度最优为例，分别采用模拟数据和实测点云数据来验证本文思想。结果表明，在求某一方向精度时将和声搜索算法加入模型中会提高方向精度，加权后也可以保证其垂直方向一定的精度。

关键词： 和声搜索算法;坐标转换;方向精度;坐标转换准则

中图分类号： P228    文献标识码： A    DOI：10.3969/j.issn.1003-6970.2020.10.027

本文著录格式：常方敏，李素敏. 和声搜索算法在坐标转换中的应用[J]. 软件，2020，41（10）：109113

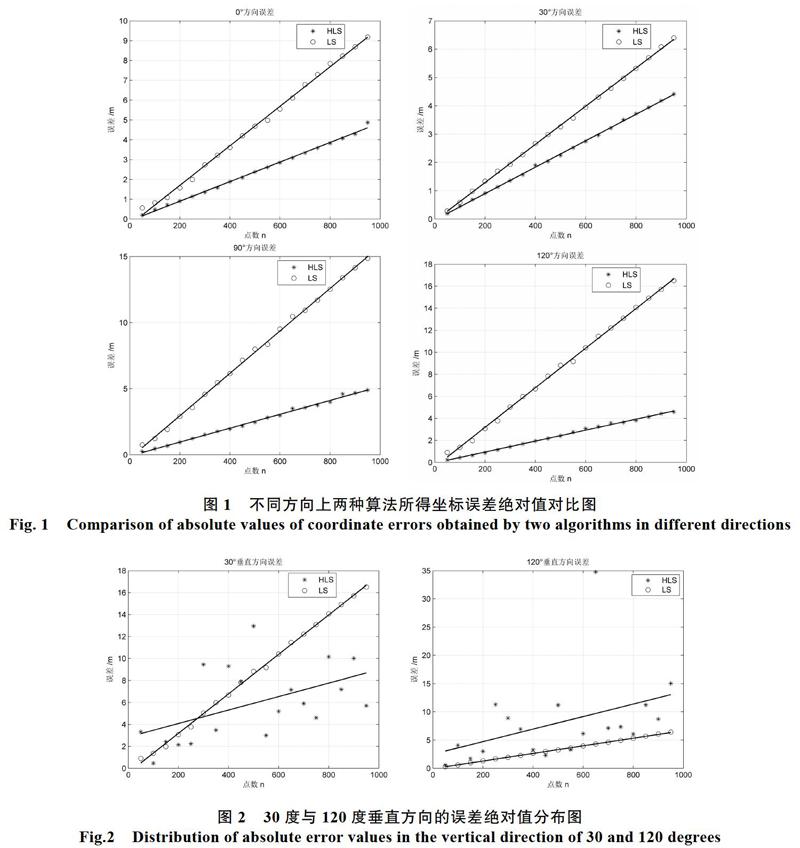
【Abstract】： Aiming at the problem that the least squares algorithm has a single criterion when dealing with coordinate transformation， this paper proposes an idea to add an intelligent optimization algorithm to the least square coordinate transformation model， so that the traditional polynomial problem of coordinate transformation is converted to the Non-polynomial problem. Through continuous iteration， the results approach the set function solution， so as to realize the diversity of the solution. In this paper， taking the best direction accuracy as an example， the simulation data and the measured point cloud data are used to verify the idea of this paper. The results show that HS algorithm is added to the model， the direction accuracy can be improved， and the vertical direction accuracy can be guaranteed after weighting.

【Key words】： Harmony search algorithm; Coordinate transformation; Direction accuracy; Coordinate transformation criterion

0  引言

在2001年，Zong W G等[1]提出了一种新颖的启发式智能优化算法——和声搜索（Harmony Search，HS）算法，由于该算法操作简单，收敛性与初始值无关，具备一定鲁棒性并且可以避免陷入局部最优等优点，因此近年来HS应用在各个领域，例如：稳健大地测量[2]、地下水位的长期预测[3]、斜坡堤护面块体[4]等等。

传统的最小二乘（Least Square，LS）算法在用于坐标转换模型存在一定的缺陷[5]。文献[6]在坐标转换模型中引入基准旋转中心，解决转换系数矩阵病态的问题。文献[7]提出基于单位四元数的任意旋转角度的三维坐标转换，解决了大角度转换的问题。文献[8]采用选权迭代的总体最小二乘算法，通过降低粗差的权重，从而得到更高精度转换参数。文献[9]在加权总体最小二乘的坐标转换模型中加入验后估计，解决了加权总体最小二乘单位权方差不同的问题。以上文献分别从LS坐标转换模型不同角度的缺陷出发，解决了一些基于LS坐标转换的问题。

本文从另一角度出发，引入启发式智能优化算法，将坐标转换这一确定性问题即P类问题转换为NP类问題，从而实现不同的优化准则，即解决坐标转换模型转换准则单一这一问题。本文将和声搜索算法，这一智能算法加入坐标转换模型中，以某一方向精度最优为例，通过模拟数据和点云数据进行对比实验从而验证本文思想。

1  基本理论与流程

1.1  和声最小二乘算法基本理论

HS算法是类比乐师反复调整不同乐器达到最优美和声这一过程。和声创作过程的音乐元素与对应数学关系如表1所示，即将最优美和声类比于最优解。每一个乐器的声音Ri（i=1，2，…，n）类比于每个解向量Xi （i=1，2，…，n），乐器的和声类比于函数解的值，其最优美和声对应的是需要求得的最优解。其中和声搜索算法包含以下几个初始变量[1]：和声记忆库（HM）、和声记忆库的大小（HMS）、和声记忆库的取值概率（HMCR）、音调微调概率（PAR）、音调微调步长（bw）。关于标准和声搜索算法的详细操作流程，请参见文献[1]。

1.2  本文算法的基本理论

基于LS算法布尔莎七参数模型方程为：

其中为目标坐标系下的坐标;为原坐标系下的坐标;为平移参数;、、分别为坐标系绕X、Y、Z轴旋转的矩阵;m为原坐标系到目标坐标系的尺度参数，通过模型方程，基于最小二乘计算准则便可得到七参数，进而通过七参数实现坐标转换。

HS并不能直接加入坐标转换模型中，因此本文对传统的HS算法进形了适当的调整，从而使其可以结合LS算法应用于坐标转换模型中。对HS的调整如下：