一种汽车白车身生产线中圆柱坐标机器人的运动学及仿真
2020-12-23郑鋆路书礼
郑鋆, 路书礼
(华晨宝马汽车有限公司,沈阳110044)
0 引 言
圆柱坐标机器人是自动化生产线中常用的一种元素,相比于传统的六轴机器人,其具有结构简单、高速、相对低廉、便于装调且具有一定柔性的特性,所以常被应用于仅需Z向变化的固定点间小件搬运系统中。在制造白车身分总成时,其小型单板件常被大量存储在含有堆叠功能的上料台内,再被送至焊装夹具上,相比于直角坐标机器人和六轴机器人,实现这个转送过程最佳的载体便是R-θ型圆柱坐标机器人,它可以在两点间实现高速、可靠且准确的低成本搬运。
1 本文描述的R-θ型圆柱坐标机器人
本文分析的搬运机器人如图1所示,其有3个自由度,分别为手臂的径向(R向)直线运动,手臂的整体旋转(θ向)运动及手臂的整体升降(Z向)运动,分别使用3个电动机实现驱动。其中手臂的径向直线运动是靠关节的耦合结构实现,这类机器人属于圆柱坐标结构。但这一水平关节机器人区别于SCARA机器人,SCARA机器人常为3个自由度,且每个关节有单独的驱动源。在末端执行器上采用销子和气磁铁设计的抓手,对工件进行抓取。可以通过升降Z轴对第一层和第二层的单板件进行抓取。

图1 R-θ型圆柱坐标机器人
2 机器人手臂关节特性推导
先研究机器人手臂,建立机器人手臂模型(R-θ向机构)时可以把带传动抽象成两个行星轮机构,因其结构设计特性实现机械运动上的单自由度约束,如图2所示。
可以从抽象后的模型看出,轮1、轮2、轮3和系杆A构成一个周转轮系,轮4、轮5、轮6和系杆B构成第二个周转轮系,且轮3和第二轮系系杆B铰接,第一轮系系杆A和第二轮系轮4铰接。当驱动系杆A即大臂壳体,则第一轮系中轮3绕轮1旋转,且轮3相对系杆A反转,带轮直径关系为d1=2d3=d6,lA=lB,又因ωA=-ω1,则有
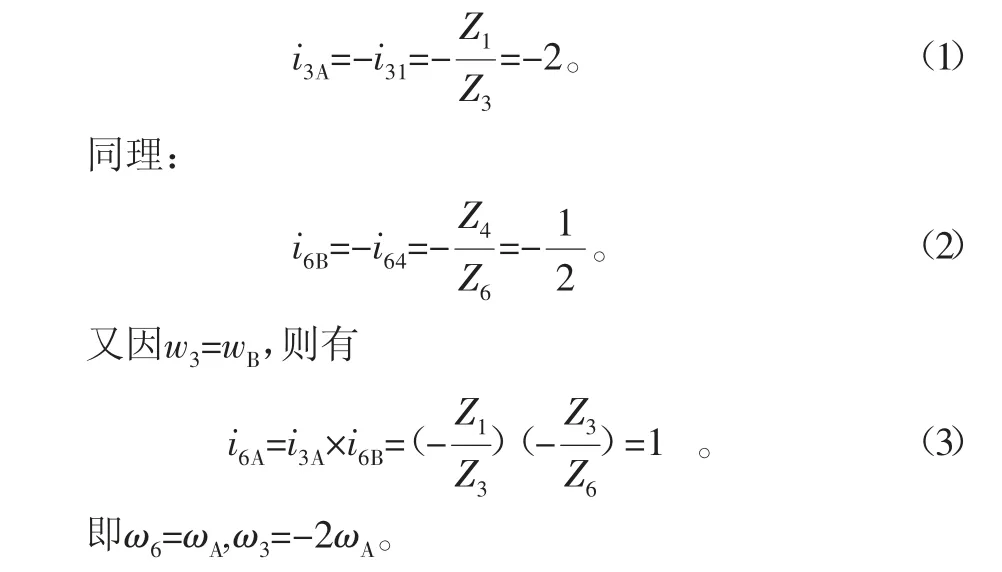

图2 机器人手臂抽象模型
3 机器人的运动学正解

图3 机器人坐标系
机器人运动学正问题是已知各杆件的结构参数和关节变量,求末端执行器的位置和姿态[1]。本文采用D-H方法建立机器人坐标系,如图3所示。

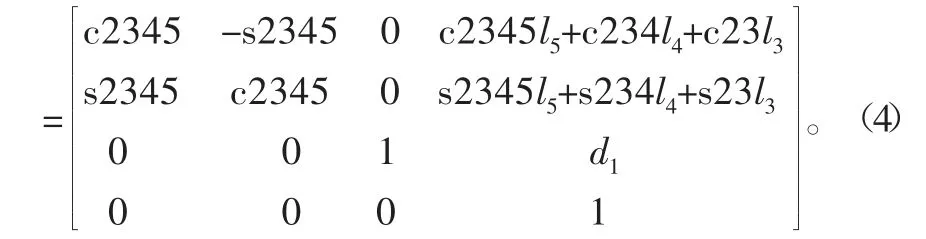
式中:c2345=cos(θ2+θ3+θ4+θ5);c234=cos(θ2+θ3+θ4);c23=cos(θ2+θ3);s2345=sin(θ2+θ3+θ4+θ5);s234=sin(θ2+θ3+θ4);s23=sin(θ2+θ3)。
代入前面手臂关节特性推导出的结论,即约束条件θ3=ω3t,θ4= -2ω3t,θ5=ω3t,同时设计时采用l3=l4=l,则手抓的姿态和位置为:

表1 关节参数
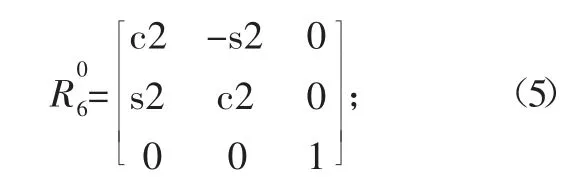

式中:c2=cos θ2;s2=sin θ2。
得到的结论说明机器人的末端执行器的姿态仅在θ2改变时发生改变,当θ2=0时,仅在x轴和z轴上变化,这个结果符合R-θ型圆柱坐标机器人的运动特性。
4 机器人的运动学逆解
机器人的逆问题是已知某满足工作要求时的末端执行器的空间位置和姿态,以及各杆件的结构参数,求解关节变量[1]。Px、Py为末端执行器的位置。可求解各关节变量:


5 机器人速度和加速度分析
速度和加速度的分析基于运动机器人的雅可比矩阵,可先得到雅可比矩阵后,再确定末端执行器速度和各关节速度和的关系。推导可得到雅可比矩阵,如式(11)所示。
建立速度关系:X.=Jq.,并代入约束条件:l4=l3=l,θ4=-2θ3,θ5=θ3,且不考虑立柱套筒的回转,即ϖ2=0,θ2=0时,

则为机器人手臂在坐标系1下的运动情况,可得出速度:

对速度求导,可得到加速度:


图4 ADAMS仿真模型
6 运动学模型的验证
以上对R-θ型圆柱坐标机器人的运动学模型进行了详细的推导,但需要对上面推导进行验证。本文使用Catia建模,然后借助ADAMS强大的运动学分析能力建立机器人运动仿真模型。但前提都是根据带轮的约束条件1:-2:1的关系,如图4所示。
通过ADAMS 仿真得出机器人末端执行器的位置、速度和加速度曲线,并使用Matlab对推导的公式进行赋值,同样分别绘制出位置、速度和加速度曲线。通过对比得知,推算结果与仿真结果是一致的,证明了推导公式和仿真的正确性。
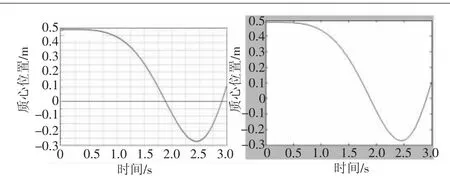
图5 X轴末端执行器质心位置曲线对比

图6 X轴末端执行器质心速度曲线对比

图7 X轴末端执行器质心加速度曲线对比
7 结 论
本文通过公式推导了R-θ型圆柱坐标机器人的运动学模型,且用ADAMS建立运动仿真模型,论证了公式推导运动学模型的正确性。在新建车身焊装生产线时,可以通过本文推导的运动学模型来设计机器人各个杆件的参数或对机器人进行选型评估,以满足生产工作对节拍和布局要求。所以本文的算法对实际工作具有重要意义,量化了评估方法,缩短了产品实现周期。
