遗传优化BP神经网络在电液力伺服系统辨识中的应用
2020-12-23周挺王虎
周挺, 王虎
(航空工业飞机强度研究所,西安710065)
0 引 言
电液力伺服系统结合了电子技术、伺服控制、液压传动和传感器技术,通过电液信号转换实现被控对象力控加载,具有功率质量比大、结构紧凑、响应快、系统刚度大、控制精度高的特点,广泛应用于飞机结构强度试验中。由于伺服阀的死区和游隙、油温和油压的变化、黏性摩擦力等影响,系统为参数时变、非线性系统[1-2]。建立系统精确数学模型可为控制系统的分析和设计提供有力依据[3],基本建立方法包括机理建模法和系统辨识建模,机理建模需要对系统做一些合理假设,通过确切的数学表达式描述系统的内部机理,系统辨识建模则是在输入和输出数据的基础上,从给定的模型类中确定一个具有与辨识系统输入输出特征相同的等价模型。多层前馈BP(Back-Propagation)神经网络作为一种反向传播学习的非线性网络,具有良好的非线性映射能力、自适应能力、并行处理和全局优化能力,能有效辨识多输入多输出的复杂非线性系统[4],但存在收敛速度较慢、对初始权值敏感、容易收敛至局部极小等缺点。遗传算法(Genetic Algorithm)是一种基于自然选择优胜劣汰和群体遗传演化的自适应概率搜索算法[5],具有很强的鲁棒性、并行计算能力和全局搜索能力。
本文采用遗传算法优化的BP神经网络对电液力伺服系统进行系统辨识建模,通过遗传算法和BP算法的混合优化,获得最佳的网络权值和阈值参数;将该辨识模型与线性参数模型的辨识结果进行比较,验证遗传优化的BP神经网络在系统辨识建模上的有效性。
1 电液力伺服系统
电液力伺服系统结构如图1所示,控制器根据载荷传感器反馈值和上位机指令值之差输出闭环控制信号,伺服驱动器实现闭环控制信号放大和转换,电液伺服阀根据驱动信号转换为对应液压负载流量,改变非对称液压缸活塞位移,将载荷施加至负载(试验件)。首先建立电液伺服系统数学模型,可为系统辨识建模提供理论依据。

图1 电液力伺服系统结构图
伺服驱动器和载荷传感器作为信号转换模块,其转角频率较系统固有频率很高,可视为比例环节,其增益分别为Kd和Kf。
电液伺服阀由力矩马达和液压放大器组成[6],第一级为双喷嘴挡板,第二级为四通滑阀,其动力学模型多采用二阶振荡环节形式,伺服阀空载流量qL0(s)满足:

式中:kq为伺服阀流量增益;kc为伺服阀流量压力增益;pL为负载压力。kq和kc值随阀工作点的变化而变化,由于阀经常在零位工作,此处阀的流量增益kq0最大,流量压力增益kc0最小,在系统分析时通常以零位系数作为阀的性能参数,kc0由伺服阀零位泄漏流量qc决定,kc0=qc/ΔpN,其中qc为伺服阀零位泄漏流量,ΔpN为额定压降。
考虑液压缸的内泄漏、外泄漏和压缩性流量,其流量连续性方程为

式中:A1为无杆腔活塞面积;A2为有杆腔活塞面积;xp为活塞位移;Ctp为液压缸总泄漏系数,Ctp=(Cec/2+Cic);Cec为液压缸外泄漏系数;Cic为液压缸内泄漏系数;Vt为液压缸两腔总容积;βe为油液的等效体积弹性模量;α为非对称缸比例系数。
忽略库伦摩擦力等非线性负载,假设负载包括惯性和弹性负载,不考虑活塞黏性摩擦力和外加负载变化,液压缸驱动力F与负载的力平衡方程为

式中:p1为无杆腔压力;p2为有杆腔压力;Ap为液压缸等效活塞面积,可近似取Ap=(A1+A2)/2;mt为折算到活塞轴上的活塞与负载的等效总质量;K为负载的弹性系数。
由式(2)~式(4)可得伺服阀空载流量输入、液压缸驱动力输出的传递函数:
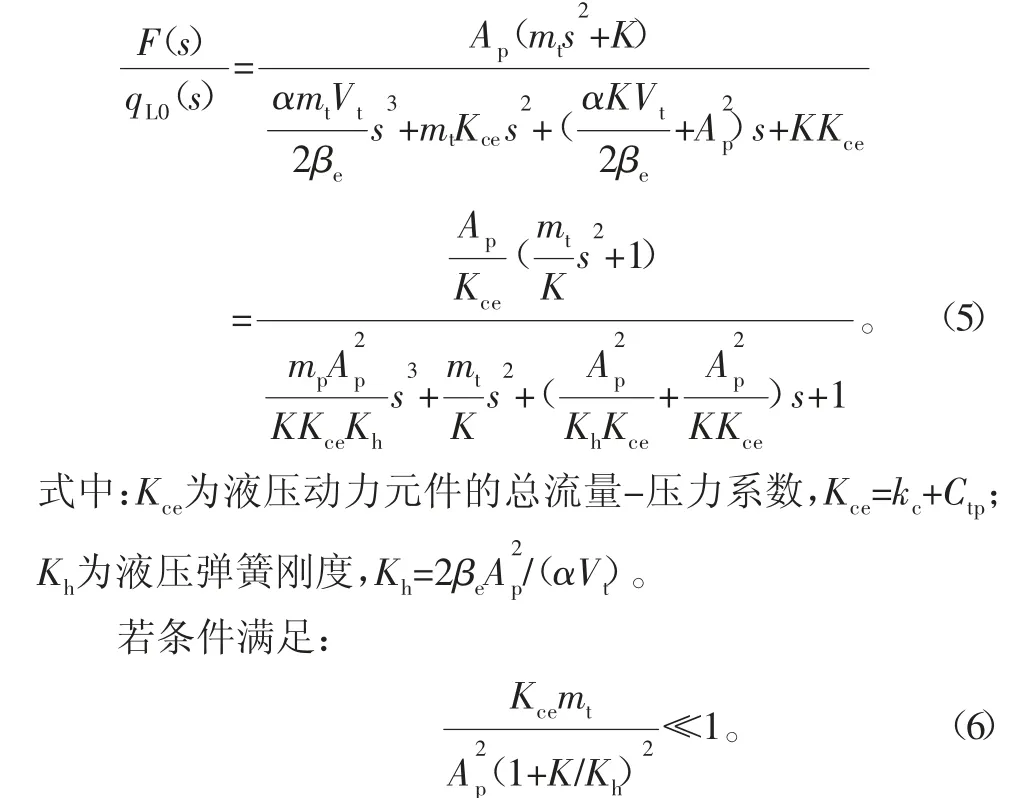
式(5)可表示为:

式中:ωm为负载的固有频率;ωr为惯性环节转折频率;ωo为振荡环节固有频率,由液压弹簧与负载弹簧并联耦合与负载质量形成;ζo为振荡环节的阻尼比。
图2为系统传递函数框图,其中C(s)为控制器传递函数。
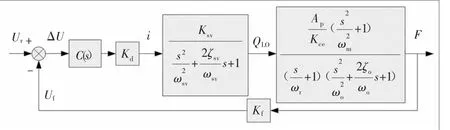
图2 系统传递函数框图
2 遗传优化BP神经网络系统辨识
2.1 BP神经网络辨识原理
BP神经网络一般为多层感知器模型,由输入层、隐含层和输出层组成,通过信号前向传播和误差反向传播周而复始对网络权值进行动态调整,使基于网络输出误差的性能指标函数达到最小,从而逼近系统输入/输出数据中的非线性映射,实现系统辨识建模[8]。图3为BP神经网络辨识建模结构,设电液力伺服系统为NARMAX(非线性扩展自回归滑动平均模型),有

式中,P为样本总量数。
2.2 BP神经网络结构
为了反映系统的动态特性,并考虑系统的辨识精度,BP神经网络输入层设4个神经元,输入值为d(k-1),d(k-2),u(k-1),u(k-2),输出层为1个神经元,为y(k)。选择隐含层层数为1,隐含层节点选取要适中,节点过少,可能造成学习过程不收敛,系统辨识精度低;节点过多,则会影响学习速度,还会由于过拟合,造成网络的容错能力及泛化能力的下降,因此确定神经元个数为10。隐含层激励函数为双曲正切函数Tan-Sigmoid,输出层激励函数为线性函数Purelin。采用LM(Levenberg-Marquardt)算法进行网络参数学习,LM算法的初始自适应学习率μ为0.001,最大训练次数为100,性能指标函数选择均方误差mse。
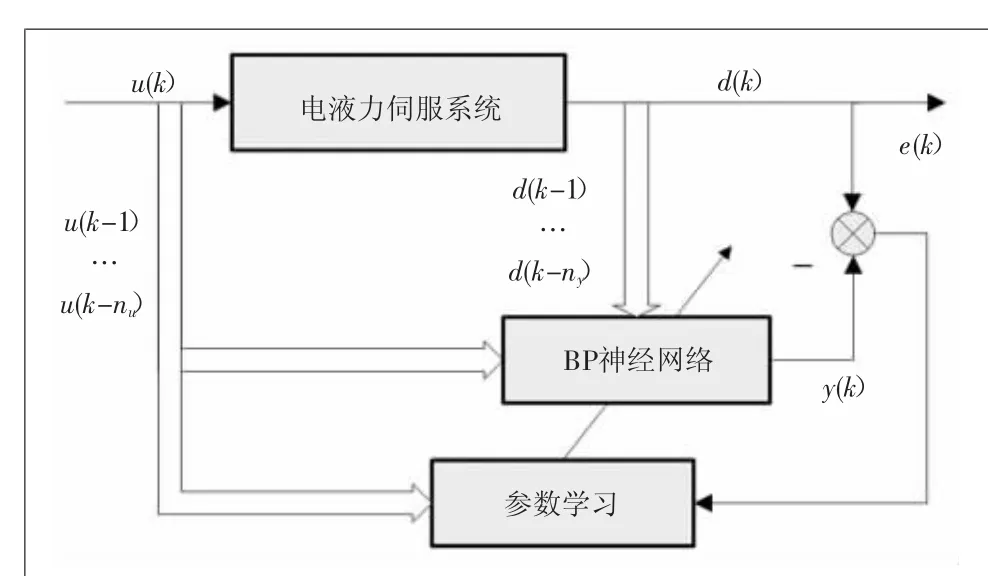
图3 神经网络辨识建模结构
2.3 初始权值和阈值的遗传优化
遗传算法从包含问题的解集中随机挑选一个群体作为初始群体,通过编码将问题的解转换为染色体或个体,根据自然选择和遗传进化机制从初始种群出发对个体进行随机选择、交叉、变异操作,按照适应度函数评估个体性能,对个体进行筛选,使群体进化到搜索空间中更好的区域,经过不断迭代,得到群体中的最优个体作为问题的最佳解[10-11]。
本文基于MATLAB全局优化工具箱,遗传优化BP神经网络初始权值和阈值的步骤如图4所示。
1)初始种群。
根据神经网络结构,采用实数编码,对网络的初始权值和阈值进行编码,编码长度为4×10+10+10×1+1=61,初始种群取值范围为[-1,1],随机产生100组长度为61的实数序列,作为初始种群。
2)适应度函数。
适应度函数val(x)采用BP神经网络的性能指标函数E,val(x)=E。
3)遗传操作。

图4 遗传优化BP神经网络初始权值和阈值
适应度尺度变换函数把适应度函数值转换为适合于选择函数使用范围的值,包括排序、比率、最佳、线性变换等函数,选择比率(Proportional)方式,返回值与个体的适应度值大小成比例;选择参数为遗传算法挑选下一代的双亲,包括随机均匀分布、剩余、轮盘赌、锦标赛等函数,选择随机均匀分布(Stochastic uniform)方式,将每一个父辈根据适应度值按比率布局在一条线上,算法以相同大小的步长沿线移动,根据降落的位置确定每一个父辈;优良个体(EliteCount)确定将具有最佳适应度值的个体遗传到下一代的个体数,取5;交叉参数说明父辈如何交叉基因产生子辈,包括分散、单点交叉、两点交叉等,选择分散(Scattered)函数,通过一个二进制向量确定子辈基因来自于第一个父辈还是第二个父辈,交叉概率取0.8;变异参数指定算法如何通过小的随机数创建变异子辈,包括高斯、均匀变异等,选择高斯(Gaussian)函数,将一个高斯分布选择的随机数加到父辈的变异个体中,第一代方差尺度Scale取1,方差压缩率Shrink取1。通过遗传算法迭代,选取最后一代种群的最佳个体,解码后将对应的权值和阈值代入BP网络进行进一步网络训练。
2.4 系统辨识算法
在MATLAB中编写遗传优化BP神经网络系统辨识程序,代码如下:
1)遗传优化BP神经网络主程序。

2)编码函数程序。
将遗传算法个体编码为神经网络的权值和阈值。


3)适应度函数。
对每一代的种群进行编码,计算神经网络下的适应度函数。

3 实验分析
搭建单通道电液力伺服系统实验台架,加载形式选用液压缸硬式连接自平衡框架,测力传感器选用10 kN,液压缸选用20 kN,油源压力21 MPa,电液伺服阀为19 L/min;设置控制器为单位增益;对系统施加周期为3.33 s的方波信号,范围为-5~+5 kN,信号采样时间为0.01 s,获取2664组实验数据。使用xlread函数将实验数据导入MATLAB工作空间,运行系统辨识程序,图5为神经网络结构,神经网络函数newff随机将数据的70%用于训练,15%用于验证,15%用于测试,图6为遗传优化BP神经网络训练的性能指标函数曲线,网络训练至第10代时网络误差已开始收敛,验证数据的性能指标函数最终为1.074×10-5。图7为数据归一化后系统实际输出与网络预测输出的对比曲线,图8为两者的误差曲线,系统误差在0.06以内,均方误差为1.497×10-5。
同时,借助MATLAB系统辨识工具箱[12],选择线性参数模型ARMAX(线性扩展自回归滑动平均模型)对系统进行辨识,模型阶次[na nb nc nk]=[4 1 1 1],采用预报误差法,辨识结果为:

图6 遗传优化神经网络训练的性能指标函数曲线

图7 实际输出与网络预测输出对比曲线
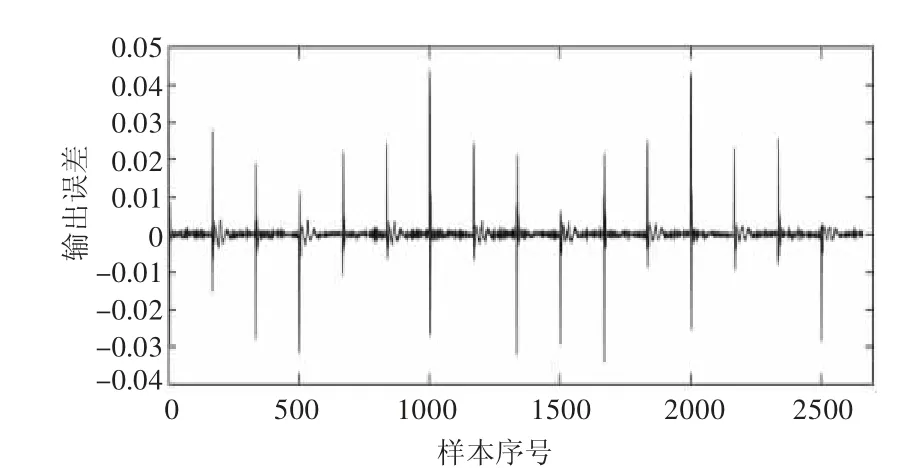
图8 误差曲线

式中:y为系统实际输出;y′为系统辨识输出;mean表示求系统实际输出的平均值;norm表示求向量的2-范数。
计算得到遗传优化神经网络模型拟合度值为99.5%,ARMAX模型拟合度值为86.04%。拟合度越高,系统辨识的结果越好,系统辨识输出值越接近实际输出值。
4 结 论
1)基于BP神经网络系统辨识建模方法不需了解系统内部机理,较机理建模法效率更高。
2)遗传算法的全局随机搜索能力有效解决了单纯BP神经网络收敛速度慢、易陷入局部极小的问题,提高了算法的鲁棒性、适用性。
3)遗传优化神经网络辨识模型较ARMAX模型辨识结果精度更高,适应性更强,为系统控制策略的改进和设计奠定了良好的基础。
