基于分形理论的滑坡变形破坏特征及演化分析

郭进雪

( 中交第二公路勘察设计研究院有限公司 武汉 430056)

受复杂地质条件、地形地貌和多变气候等因素的多重影响，滑坡灾害在我国频发。而库岸滑坡形成环境的特殊性和复杂性，均给研究增加了难度。

库岸滑坡的变形破坏特征与库水位的变动及降雨呈现出极大的相关性。库水位对滑坡动态、复杂的物理力学效应，使得其变形和破坏也具有复杂特殊性，且往往与时间、库水位的升降速率成正比[1]。而降雨因子是通过物理软化和渗流等对库岸滑坡产生影响的[2]。

研究滑坡孕育、发展及演化规律的方法众多，多方学者采用位移、地下水、应力等特征参量，辅以宏观地表变形特征进行滑坡演化阶段的判别。裂缝是判断滑坡变形与破坏最直接的标识，分形理论作为定量刻画系统非线性的有效手段，可对其进行有效定量评价[3]。

本文通过监测数据和数值软件考虑在内外因素影响下典型库岸滑坡的变形及破坏规律，运用分形理论分析滑坡演化特点，为库岸滑坡的防治工作提供一定的参考借鉴，以期为工程项目的建设和环境保护提供一定参考。

1 工程概况

白水河滑坡位于湖北省秭归县，其山水环绕，是典型的库岸滑坡，滑坡全貌图见图1。据钻孔资料和现场调查，后缘的拉裂缝是其边界，前端的剪出口常被水淹没。滑坡的长与宽分别为600 m和700 m，是深层大型土质滑坡。

图1 滑坡全貌图

滑体厚度分布不均，呈现从后到前增大的规律，白水河滑坡剖面图见图2。白水河滑坡滑带特征图见图3，上滑带厚0.9～3.13 m，以粉质黏土为主，夹有少量碎石，埋深12～25 m；下滑带为含炭质粉砂质泥岩，由透水性差的薄层含炭质泥岩组成，埋深18.9～34.1 m。

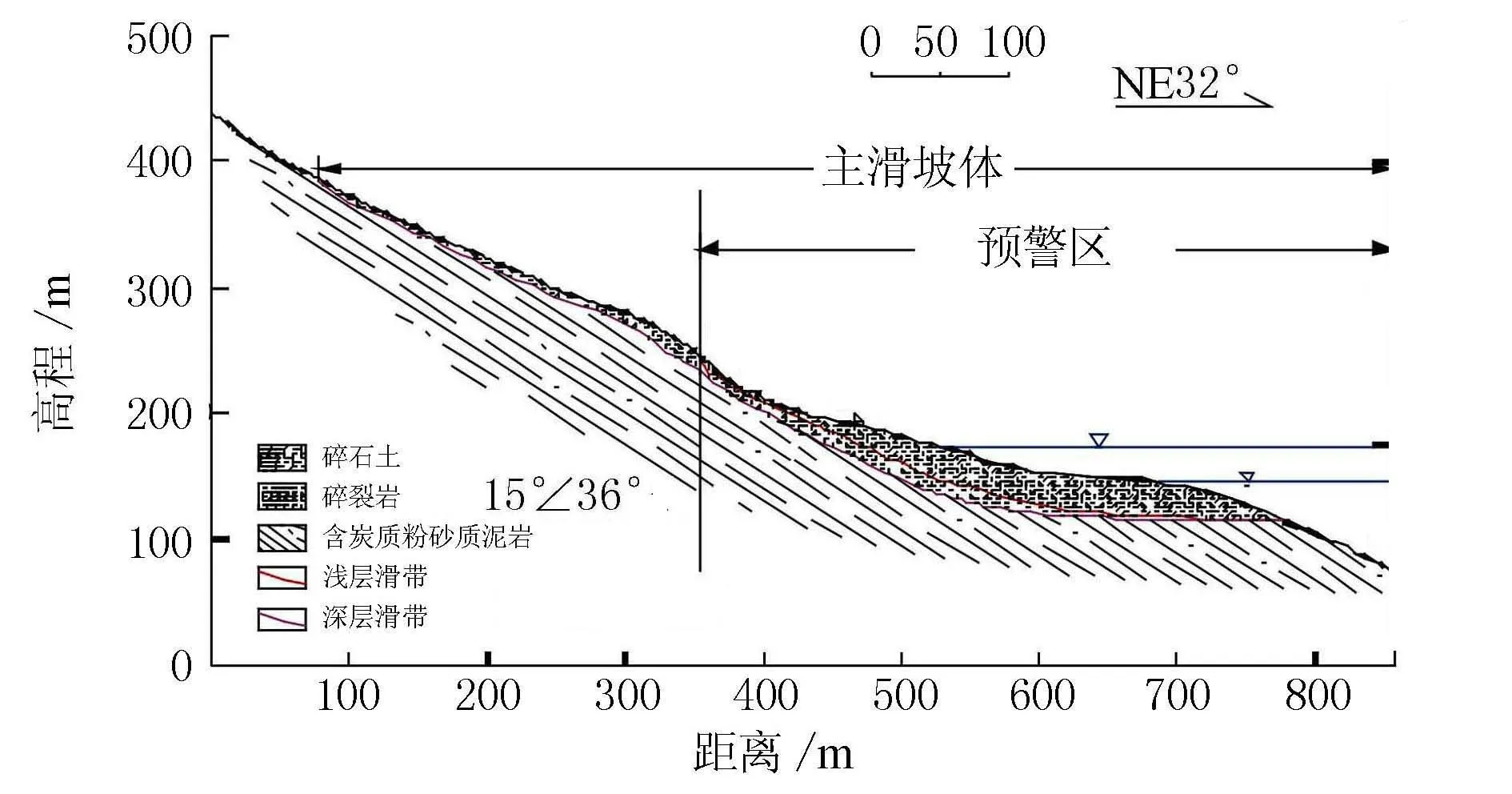
图2 白水河滑坡剖面图

图3 白水河滑坡滑带特征图

2 白水河滑坡变形监测数据分析

2.1 位移监测分析

2007年5月24日在白水河滑坡体上布设了11个相对位移监测点，2015年5月8日选测部分监测点，其结果见表1。

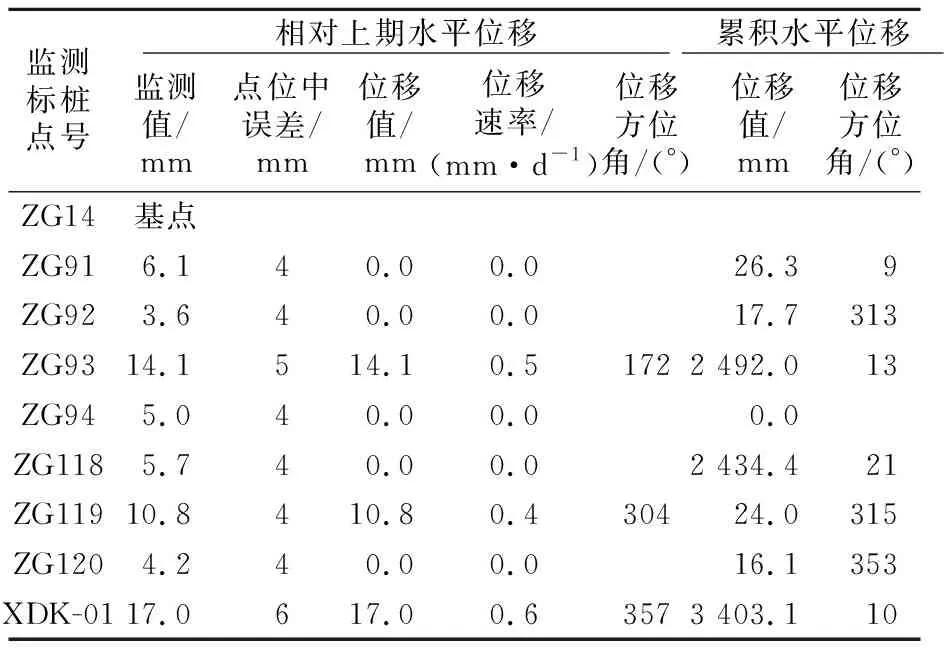
表1 白水河滑坡2015年5月8日GPS监测结果

根据GPS和钻孔倾斜的监测结果，可知在2015年滑坡前缘东侧XD-01发生小幅位移而其余7个测点无明显位移，XD-01测点位移为局部位移，主要受三峡水位下降所致，地表可见局部迹象。在此期间，滑坡预警区存在局部变形，整体变形不明显，滑体仍处于欠稳定状态，预警区外滑坡无明显位移，滑体处于基本稳定状态。

2.2 库水位及降雨监测数据分析

库水变动及相应的降雨数据见图4。

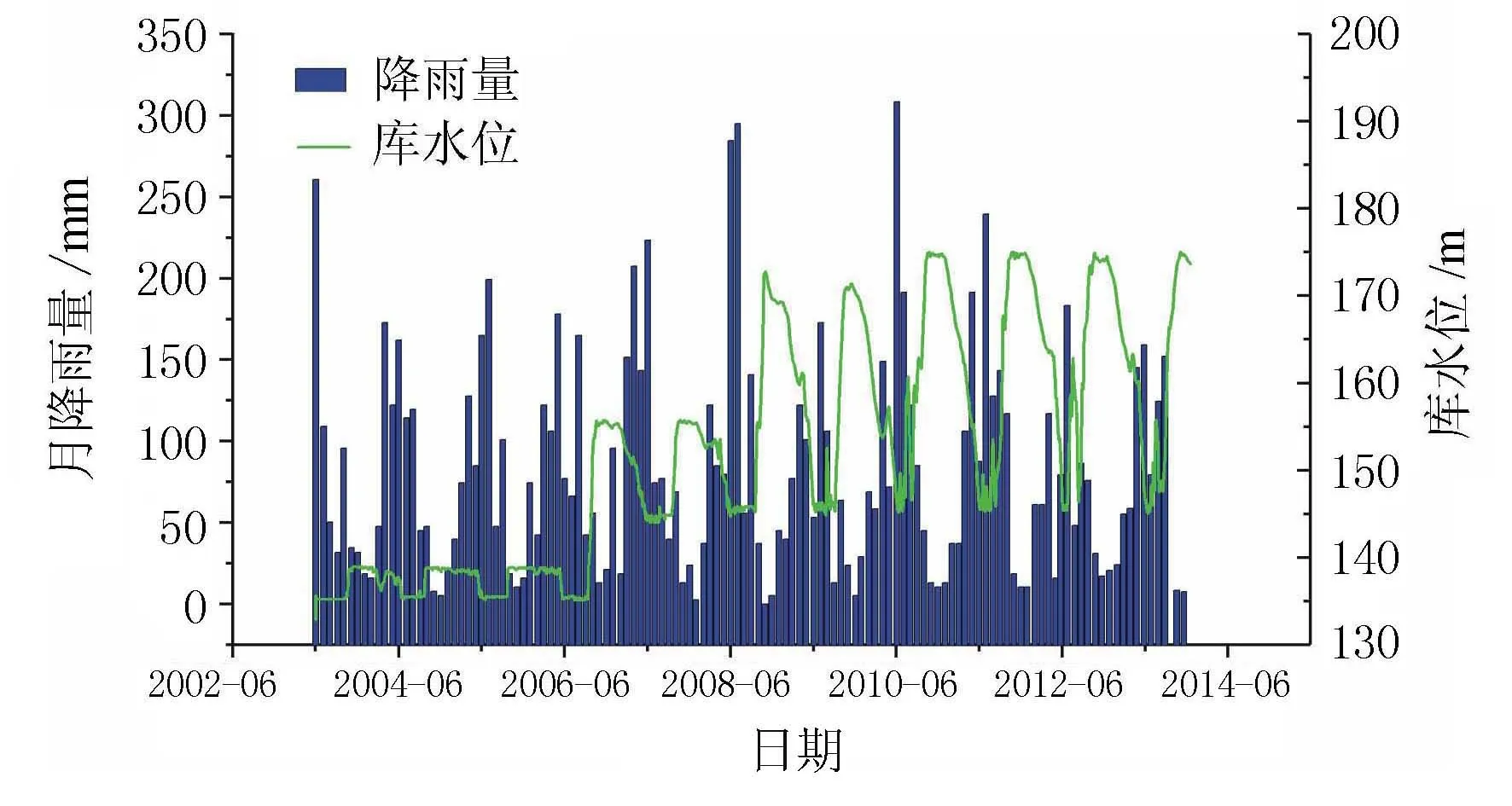
图4 库水位调度及每月降雨量情况

由图4可知，2003-2015年库水位调度经历了3个阶段，分别以2006、2008年为时间节点；降雨具有年内周期性变化的特点，最大降雨量200 mm一般在6、7月份，每年冬季为降雨量较少时期，基本在50 mm以下。

库水位变动、降雨分布及监测点位移增量见图5。

图5 滑坡降雨量及位移增量随时间变化图

由图5可见，往往在降雨量较大的时间点之后一段时间才出现大的位移增量。库水位开始下降时刻与滑坡最大位移增量有同样的关系，这再一次验证了滑坡变形速率与外界影响因子作用间的滞后性。

3 白水河滑坡数值模拟分析

本文综合考虑各因素，选取剖面2-2′(对应监测点ZG118、ZG119和ZG120)和3-3′(对应监测点ZG92与ZG93)进行参数反演。

3.1 计算模型的建立

将剖面导入GeoStudio软件中，建立相应的滑坡地质力学模型，见图6。网格间距设置为5 m。模型底部及两侧设为固定边界；滑坡面上存在降雨和库水位波动2种因素的作用；基岩视作隔水边界。岩土体物理力学参数见表2。

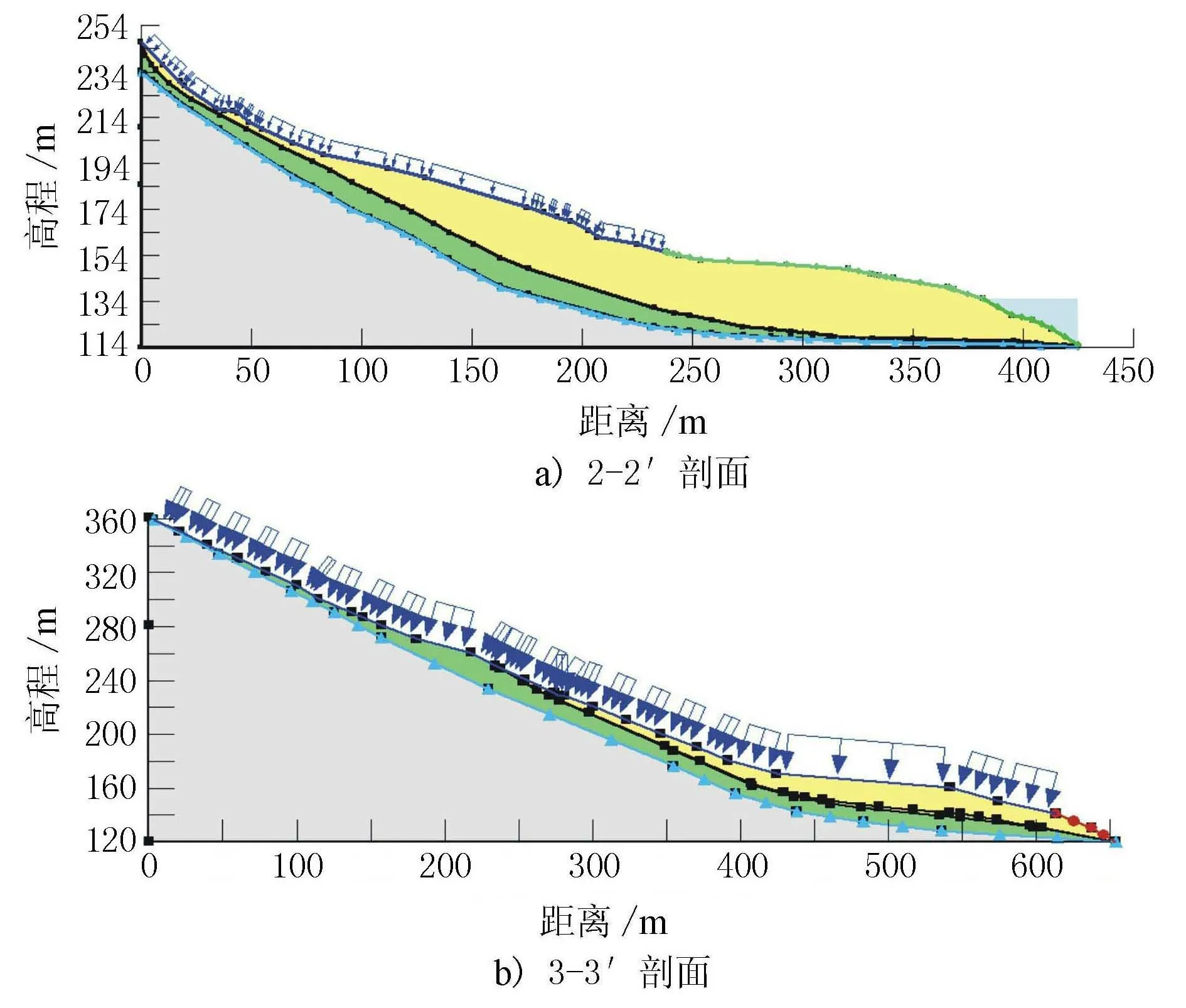
图6 白水河滑坡模型图

表2 滑坡岩土体物理力学参数

3.2 参数反演确定模型计算参数

库岸滑坡的发育过程与降雨及库水位有密切联系，且后两者均具有显著的周期性。因此以年为单位，通过调试滑带c、φ值的参数组合，得到多组模拟位移-时间曲线，与实际数据进行对比，确定不同时间段滑带的参数。时间划分见表3，反演后对应的滑带参数取值见表4。ZG93和ZG118的累计位移-时间曲线见图7。

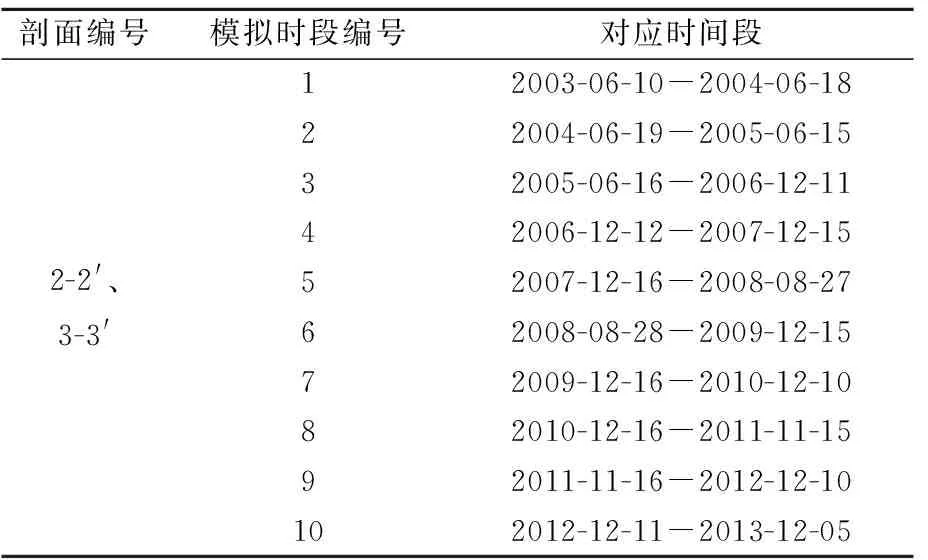
表3 剖面反演时段划分

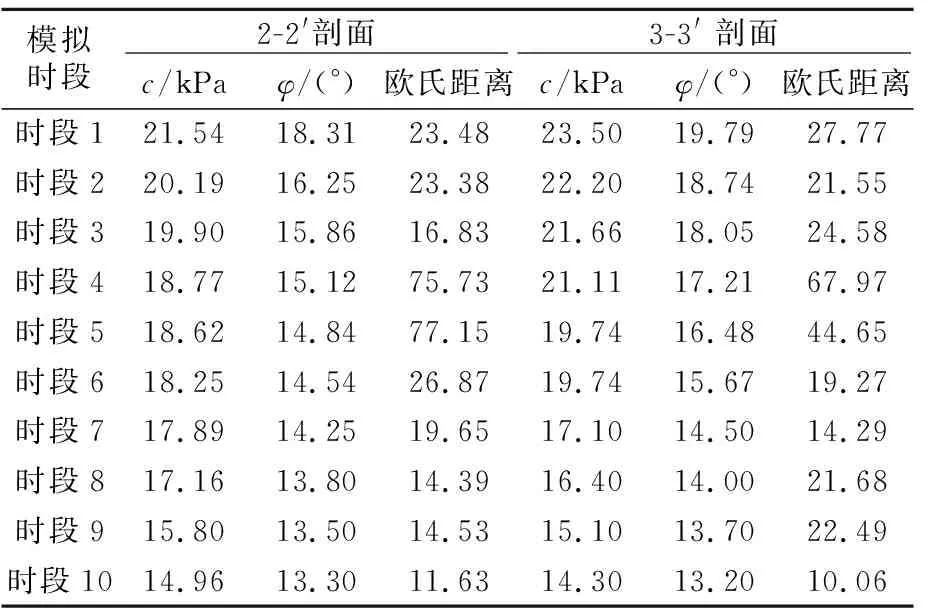
表4 2-2′和3-3′剖面滑带强度参数最优取值

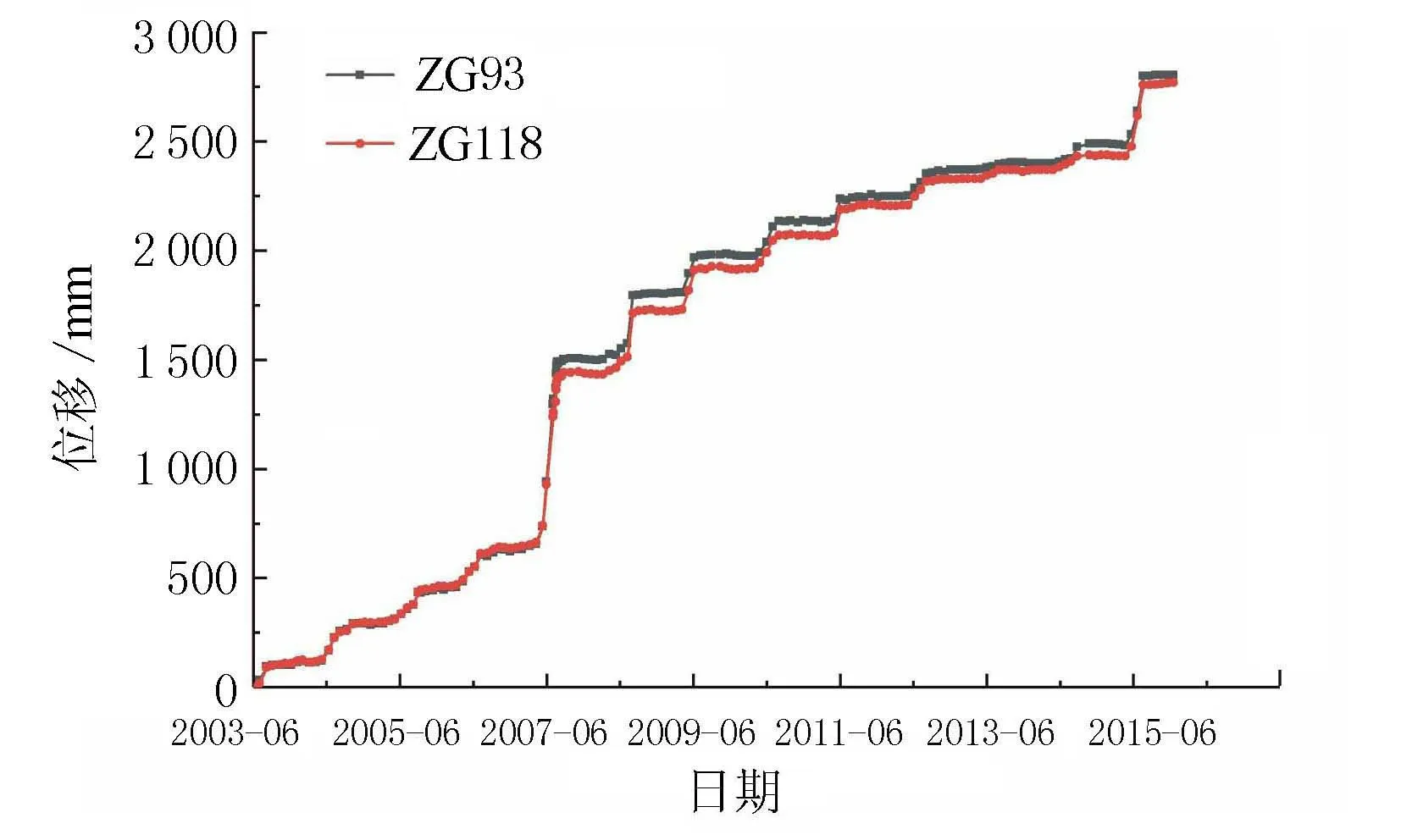
图7 GPS监测点累积位移监测曲线

2-2′与3-3′剖面滑带强度参数弱化图见图8。

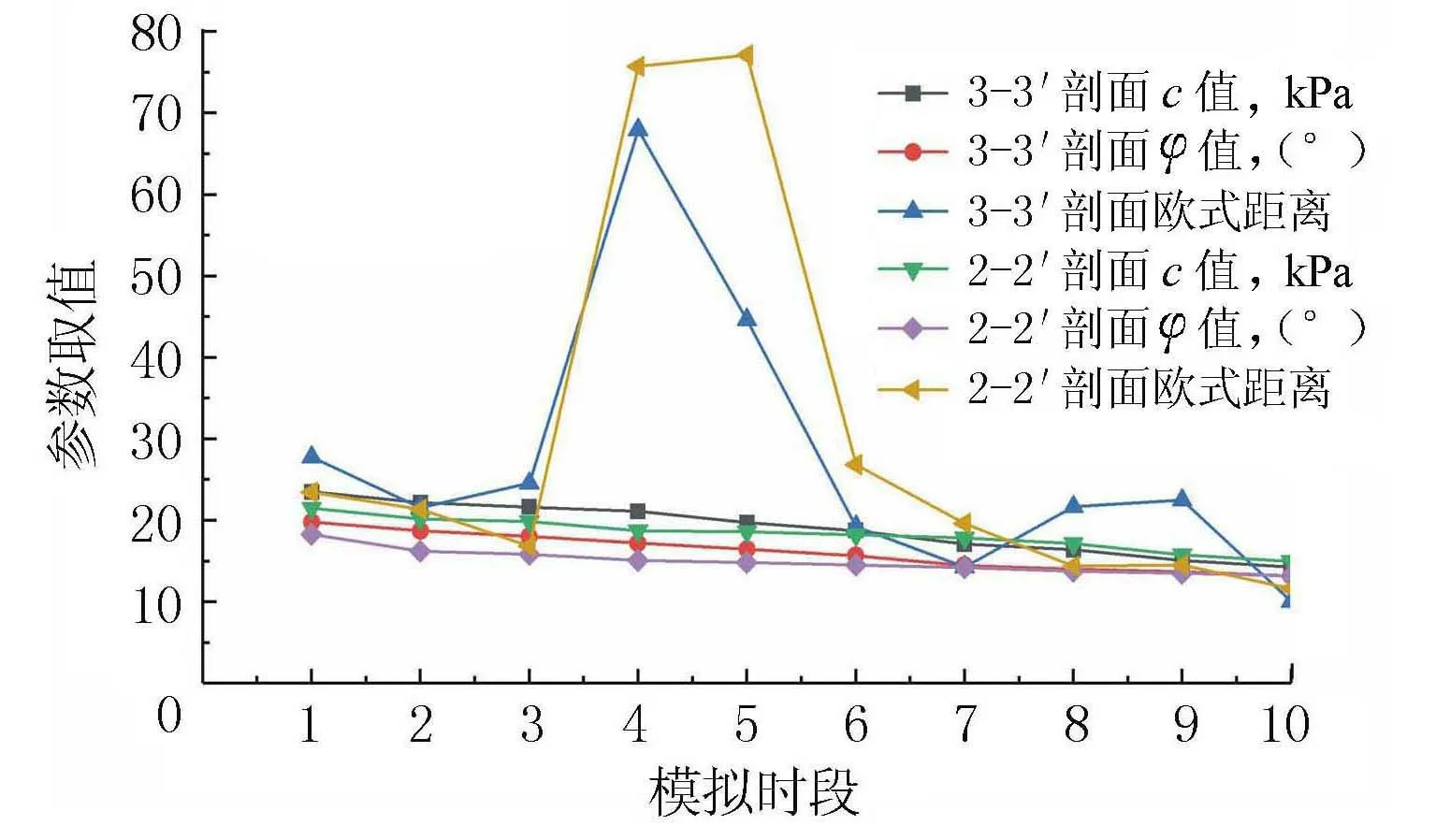
图8 2-2′与3-3′剖面滑带强度参数弱化图

由图8可知，2-2′和3-3′剖面的c、φ值均随时间的推移而呈现出近似直线的衰减规律，且其衰减程度逐渐趋小。欧式距离代表着实际监测数据与模型中数据的差异，除了4和5模拟时段的差异相对较大外，其他模拟时段的差异都非常小，数值模型具有较高的精度。

3.3 滑坡渗流场的变化特征分析

渗流是导致滑坡产生变形的主要原因，通过SEEP/W模块进行渗流数值分析，获取渗流场随时间的演化规律，地下水位线分布见图9。

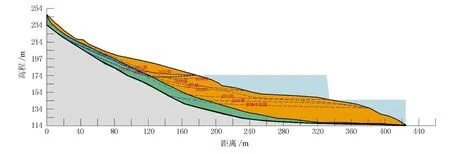
图9 滑坡地下水位线分布图

由囷9可见，2003年6月地下水位在135 m附近，在2004年6月-2005年6月，滑坡中前部位的地下水位线有较小幅度的提高，后缘则攀升到高程接近220 m的位置，这是由于降雨入渗到坡体内部而不能及时排泄出所致。2006年1月-2007年12月，地下水位线随着库水位的提高而出现一定程度的增高，后缘高度维持不变。2008年1-12月滑坡内部浸润线相比上一年下降较多，而后缘却有一定程度的提高。之后几年地下水位线的变动不大。

白水河滑坡孔隙水压力分布见图10。

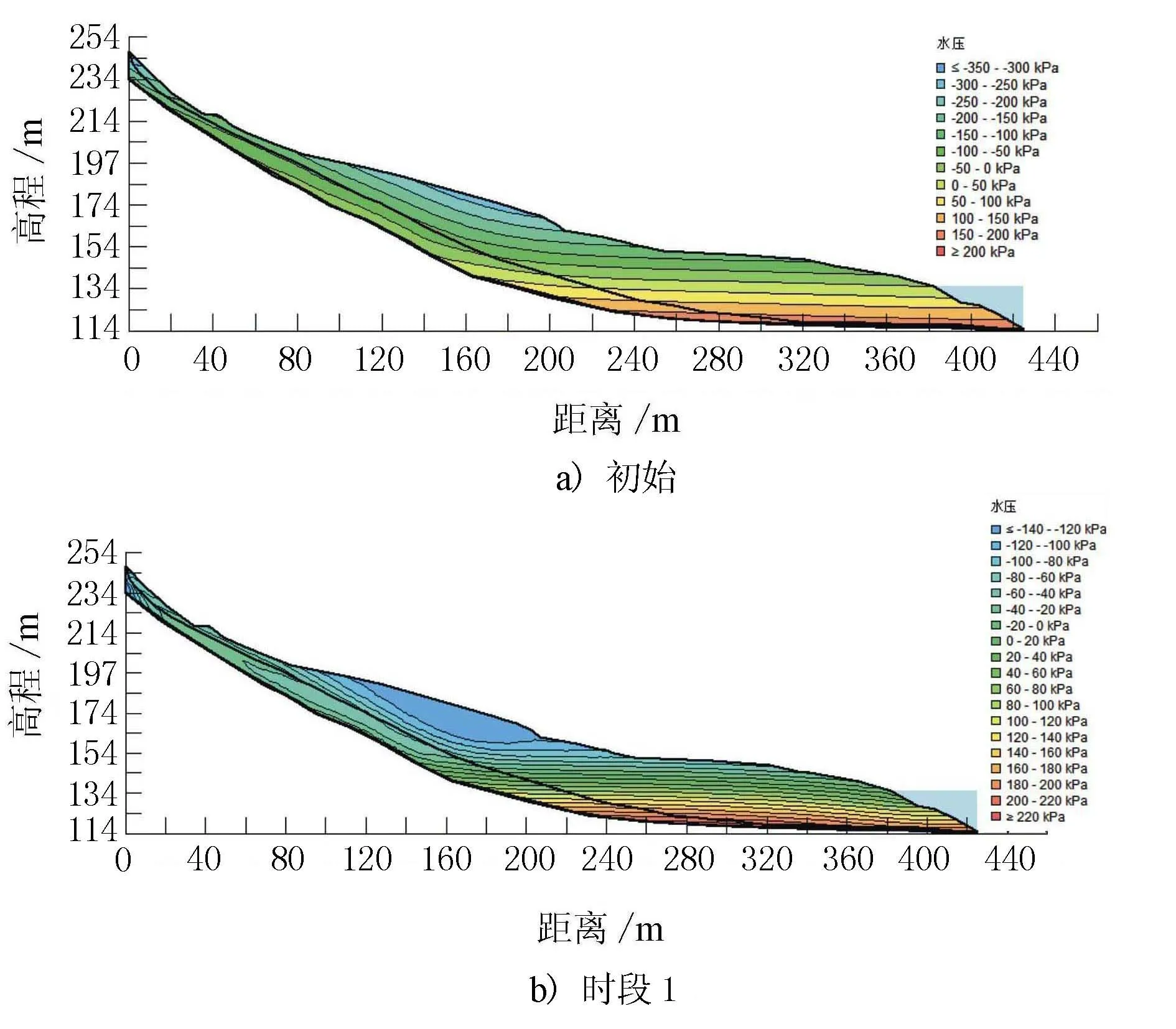
图10 白水河滑坡孔隙水压力分布图

由图10可见，初始阶段，在坡顶和滑体的中上部，孔隙水压力达到了最大负值-350 kPa。越深入滑坡内部，孔隙水压力逐步增大。在模拟时段1，最大的负孔隙水压力为-120～-140 kPa；滑坡后缘的孔隙水压力开始收敛；最大正孔隙水压力的数值有所提高。与模拟时段1相比，时段2正孔隙水压力区域范围和数值均有提高。而模拟时段3、4的最大负孔隙水压力分布相似；最大正孔隙水压力进一步提高；时段4在坡脚出现局部负孔隙水压力。模拟时段5的最大孔隙水压力有所降低。模拟阶段6～10的孔隙水压力分布情况基本无变化。

3.4 滑坡变形特征分析

渗流分析后通过SIGMA/W模块，选取剖面3-3′布设监测点W1～W5系列对滑坡的变形特征进行分析，具体坐标略。

白水河滑坡W1～W5监测点系列位移-时间图，见图11。

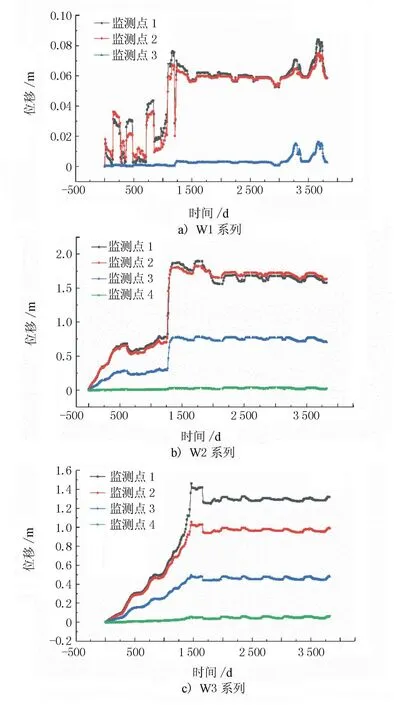
图11 白水河滑坡W1～W5监测点位移-时间图

由图11可见，每个监测点系列中的位移变化规律相似，且随着监测点位埋深的增加而减小。W1点系列均位于135 m库水位之下，其位移呈波动性上升到0.07 m后，维持在0.06 m附近，一直处于较微小的状态。

W2与W3中的监测点位于135～175 m库水位之间。W2监测点在位移突增后，维持在较平稳的状态。W3监测点的位移开始呈近乎直线形地上升，然后维持稳定。W4与W5的监测点中，仅W4中的监测点4会受到172～175 m库水位的影响。W4中监测点发生第一次较大位移突变后，监测点4变形基本维持稳定，其他监测点则呈阶梯状上升。W5中监测点1～3的位移数值高度一致，监测点4的位移值略低。

3.5 滑坡稳定性分析

继承渗流场结果后，选择Morgenstern Price(M-P)法进行滑坡的稳定性数值分析。

白水河滑坡稳定性系数随时间变化曲线，见图12。

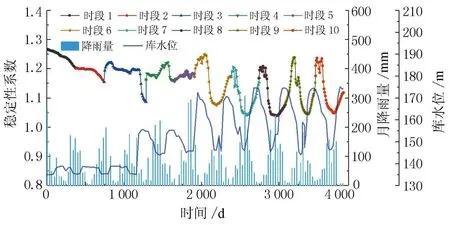
图12 白水河滑坡稳定性系数随时间变化图

由图12可见，模拟时段1的稳定性系数较高，这是降雨和库水位作用，从而使滑坡内部应力状态发生较大的改变；模拟时段2～5的安全系数为1.17左右，在模拟时段2～3的末期其降低幅度较大，这是由于库水位下降引起超孔隙水压力产生，以及降雨造成渗透压力增加；而模拟时段6～10稳定性系数的变化幅度均较大(1.05～1.20)，这是由于库水位涨落的差距有近30 m，对滑坡中下部岩土体的受力形式产生了影响。此外，滑坡的稳定状态按GB/T 32864-2016可划分为4种类型，详见表5。

表5 滑坡稳定性划分表

2003年6月-2015年12月，其稳定性在稳定、基本稳定和欠稳定3种状态间变化。在时段1～5，滑坡的稳定性系数基本大于1.15，从时段6的后半部分开始，滑坡进入基本稳定阶段。虽然滑坡的安全系数一直大于1.0，但安全系数最小时仅为1.03，滑坡处于欠稳定状态。因此，在每年的雨季以及库水位下降期，均是需对滑坡变形破坏加以防范的关键时期。

4 基于分形理论的白水河滑坡裂缝发展规律分析

4.1 白水河滑坡宏观裂缝发育情况

白水河滑坡属于牵引式滑坡，根据滑坡的力学破坏机制及裂缝分期配套规律[4-5]，斜坡演变阶段规律和裂缝空间特性的对应联系见图12和13。地表裂缝开展过程具体可分为如图14所示的4个阶段。

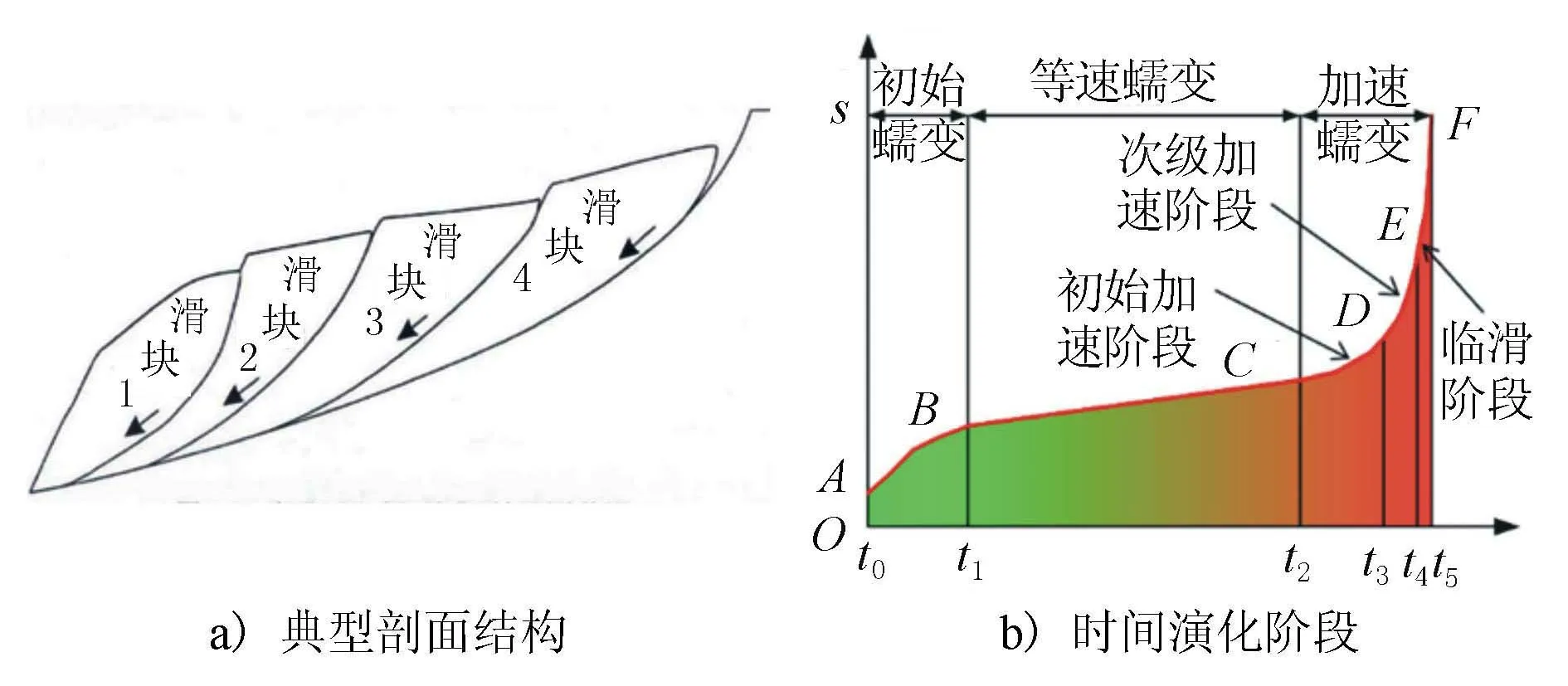
图13 牵引式滑坡典型剖面结构图及时间演化阶段

1) 裂缝发展前期。滑坡前缘及临空面旁拉张裂缝形成。坡脚处由于应力累积，致使岩土体拉裂，其形态见图14a)。此时，滑坡在初始变形阶段。

2) 裂缝发展中期。滑坡裂缝向后扩张。前部裂缝的形态不断发展，当变形增加到某一极限时，滑块脱离母体。新的临空面产生新的拉张裂缝，其形态见图14b)。此时，滑坡在匀速变形阶段前期。

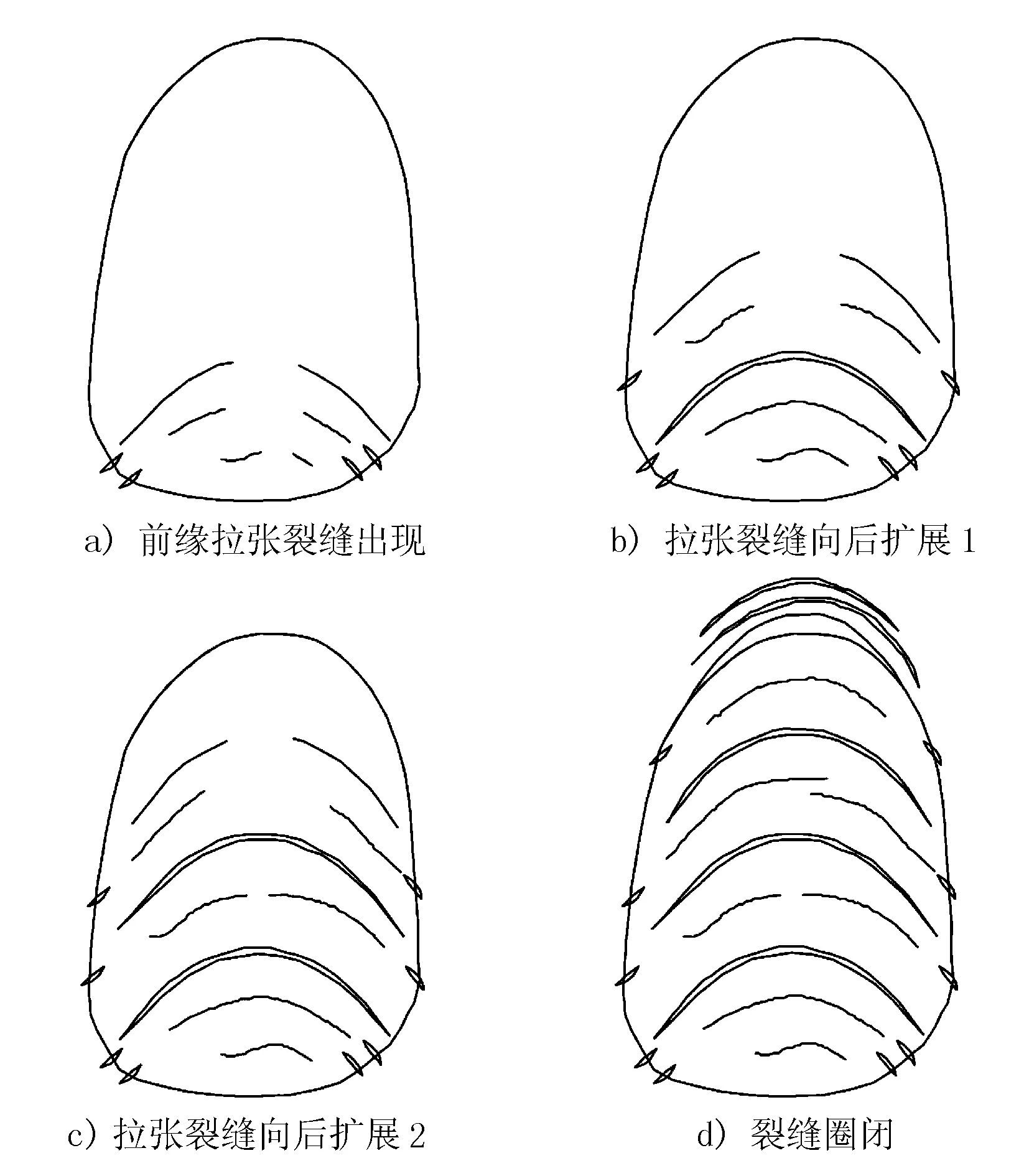
图14 牵引式滑坡地表裂缝形态简图

3) 裂缝发展中后期。裂缝持续发展，分布到了滑坡中后部及边界。滑移量较大的滑块与坡体分离，重复1)与2)中的发展规律，最终裂缝持续发育到了滑坡后缘。期间形成弧形拉裂缝和下错台坎等，其形态见图14c)。滑坡处在匀速变形阶段后期。

4) 裂缝发展末期。地表裂缝扩展到滑坡后缘，且裂缝圈闭，其形态见图14d)。此时，斜坡位于加速变形阶段。

4.2 基于分形理论的滑坡裂缝发育分析

B. B. Mandelbrot利用分形维数D来定量刻画分形的复杂程度，并给出了计算方法[6]见式(1)。

(1)

式中：Nn为基本单元中折线段的段数；r为每条折线段的线度；D为分形维数；C为比例常数。通过公式变换，得到

(2)

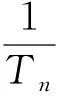
(3)

在MATLAB中编制程序，对裂缝空间形态特征图形进行处理，通过提取曲线灰度值来获取曲线的分维数D。计算结果见表6。

表6 裂缝不同演化阶段分形数值表

经过地质调查和研究区的相关资料，白水河滑坡地表裂缝的分布见图15。

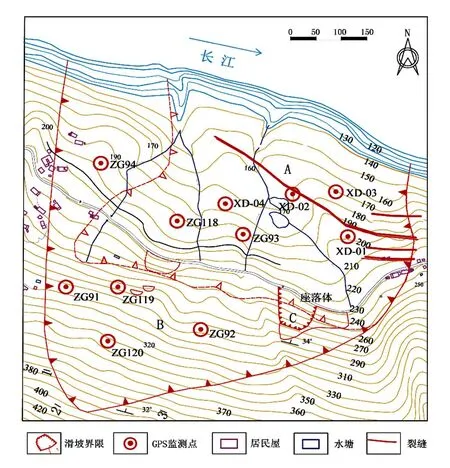
图15 白水河滑坡裂缝分布平面图

滑坡边界的分形维数为1.278。由于裂缝分布于主滑体上，因此以主滑体的边界为范围，进行图形的处理。用MATLAB编制程序进行不同阶段滑坡分形维数的计算，其中2009年滑坡裂缝发育的分形维数值为1.304，到2012年12月计算所得的结果为1.341。由此判断，白水河滑坡在2012年裂缝发育仍然处在阶段1)。

5 结论

1) 根据白水河滑坡上监测点的位移数据及研究区降雨和库水的资料分析表明，变形主要集中在预警区内，预警区外的变形较微小；降雨呈现年内的周期性变化，2008年以后为库水影响较大时期。滑坡变形速率与降雨量大小和库水位的下降速率成正比，且与2个影响因子在时间上存在滞后性。

2) 在滑坡的渗流场分析中，随着模拟时段的增加，最大孔隙水压力持续增加；滑坡的孔隙水压力具有高程分带的特征。滑坡的位移场变化特征表明，变形具有随高程变化的特点，常年浸泡在135 m水位以下的部分变形不大，而在滑坡的中部位于135～175 m库水波动区具有较大变形。滑坡的稳定性分析表明，滑坡在欠稳定与稳定之间变化(Fs=1.05～1.25)。

3) 滑坡呈现渐进牵引式破坏，由裂缝不同演化阶段分形数值表可初步判断2012年白水河滑坡仍处演化阶段①，即初始蠕变阶段，与实际相吻合。