连续刚构桥悬臂施工中腹板斜裂缝分析与控制

2020-12-23成厚松

交通科技 2020年6期

刘超郭夏成厚松

(中国市政工程中南设计研究总院有限公司武汉 430010)

随着我国基础设施建设的不断发展，许多大跨径的连续梁、连续刚构建设基本都采用挂篮施工的方法。在挂篮施工过程中，腹板沿波纹管方向的斜裂缝已经成为一种常见的工程病害。在现行规范[1]中，对于此类劈裂裂缝并未做定量的分析规定，大量的研究也只是停留在定性分析阶段。在实际工程项目中，设计人员只能凭借以往经验进行设计。本文通过建立midas纵向总体模型和ANSYS锚下局部模型进行对比分析，寻找裂缝产生的受力机制，以期提出量化计算此类裂缝的公式。并以一座在建桥梁为研究对象，从设计和施工两方面分着手，寻求导致混凝土开裂的主要原因及防止此类裂缝出现的设计方法和思路。

1 工程背景

某预应力连续刚构桥跨径为75 m+130 m+75 m=280 m，桥宽20.5 m，单箱双室，体内、体外混合配束。梁高2.5～7.5 m，腹板厚60～80 cm，底板厚30～80 cm(1.8次抛物线)，顶板28 cm。主梁混凝土标号C50，采用挂篮悬浇施工，节段长度3～4 m。每个节段布置3束19-15.2顶板束、6束15-15.2腹板束，均分布置于3条腹板上。

施工过程中，2～4号节段的部分腹板出现不同程度的斜向裂缝。经第三方检测机构检测，沿波纹管方向的裂缝长度约为75～270 cm，裂缝宽度约为0.06～0.12 mm，未漏浆裂缝深度约为26～43 mm，裂缝起始于距离锚头1 m左右处，且长度未超过当前块段范围。漏浆裂缝因裂缝堵塞无法检测裂缝深度。裂缝发生在腹板束全部张拉后，且在对称位置，裂缝并未对称出现。

2 midas平面杆系模型分析

为了判断裂缝的开展是由于整体受力还是局部受力导致的。本文采用midas Civil建立了全桥整体模型。模拟了挂篮施工的整个过程。midas纵向整体模型见图1。

图1 midas纵向整体模型

本文选取施工过程中，第4号节段张拉预应力后的应力情况进行分析。在整体模型中，4号块在纵向预应力张拉后，主拉应力为0.5 MPa。最大主拉应力图见图2。

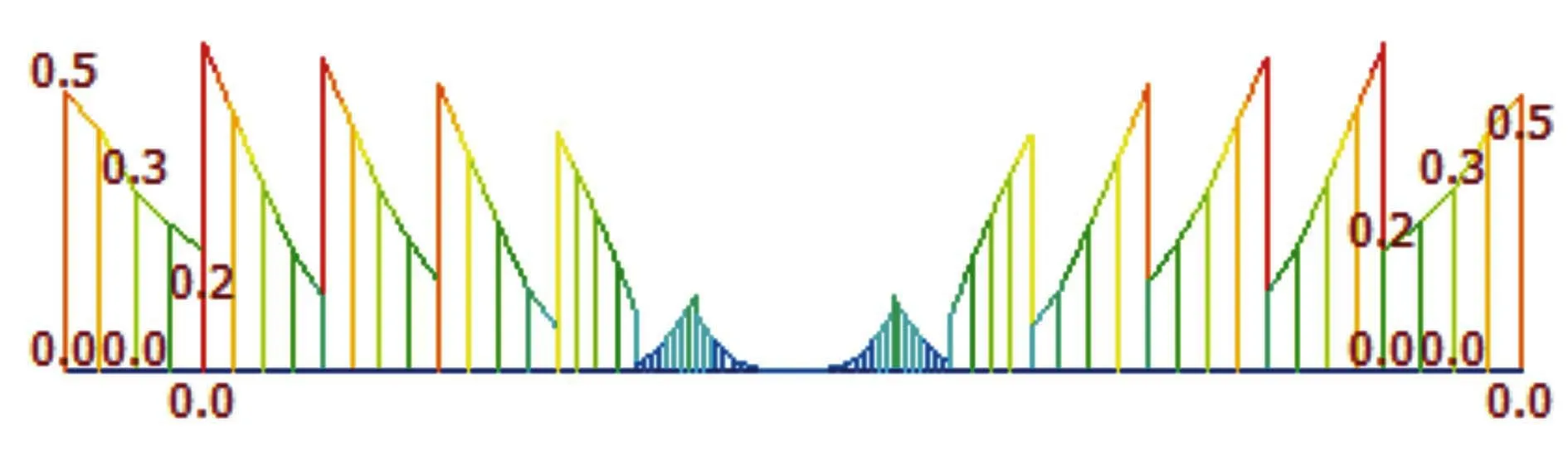
图2 最大主拉应力(单位：MPa)

由计算可知，该工况下，混凝土主拉应力水平较低，远小于混凝土的抗拉强度。纵向整体模型计算满足规范要求。并且，通过裂缝的走向、形态、位置，综合判断此类裂缝不是结构整体受力裂缝。此类裂缝应为局部拉应力过大而产生的局部裂缝。以往研究表明，预应力锚固端在距离锚头一定位置存在较大的锚下劈裂力，是导致此类裂缝形成的主要因素之一[2-4]，本文主要研究劈裂力对裂缝的影响。

3 锚下劈裂应力简化计算

3.1 最大劈裂应力计算方法

预应力锚下劈裂力的大小直接决定了是否会产生波纹管纵向裂缝。文献[2]提出了针对预应力锚下劈裂应力的计算公式。

最大横向拉应力计算方法见式(1)。

(1)

式(1)中，劈裂力合力作用方向垂直于预应力钢束轴线，以轴心受拉的受力模式简化计算受拉截面的平均应力水平，再通过实验数据得到的最大应力与平均应力的比值，由此可得到锚下劈裂应力的最大值。通过对平均劈裂应力与最大劈裂应力的计算，可以判断混凝土截面的主拉应力水平。当最大锚下劈裂应力过大时，截面可能会出现裂缝。

3.2 劈裂力合力及作用点位置计算

文献[1]提出了锚下劈裂力合力的计算公式。锚下劈裂力合力设计值计算方法见式(2)。

Tb,d=0.25Pd(1+γ)2[(1-γ)-

(2)

式中：Pd为锚固力设计值，N，取1.2倍张拉控制力；a为锚垫板宽度，mm；h为截面高度，mm；α为力筋倾角，(°)；γ为偏心率，γ=2e/h。

锚下劈裂力合力作用位置距离锚固端面的水平距离，计算方法见式(3)。

db=0.5(h-2e)+esinα

(3)

式中：e为锚固力偏心距，mm；

图3给出了预应力锚下劈裂应力的分布情况。由图3可知，距离锚头一定位置处，确实存在劈裂拉应力，通过应力积分得到劈裂力合力Tb,d。

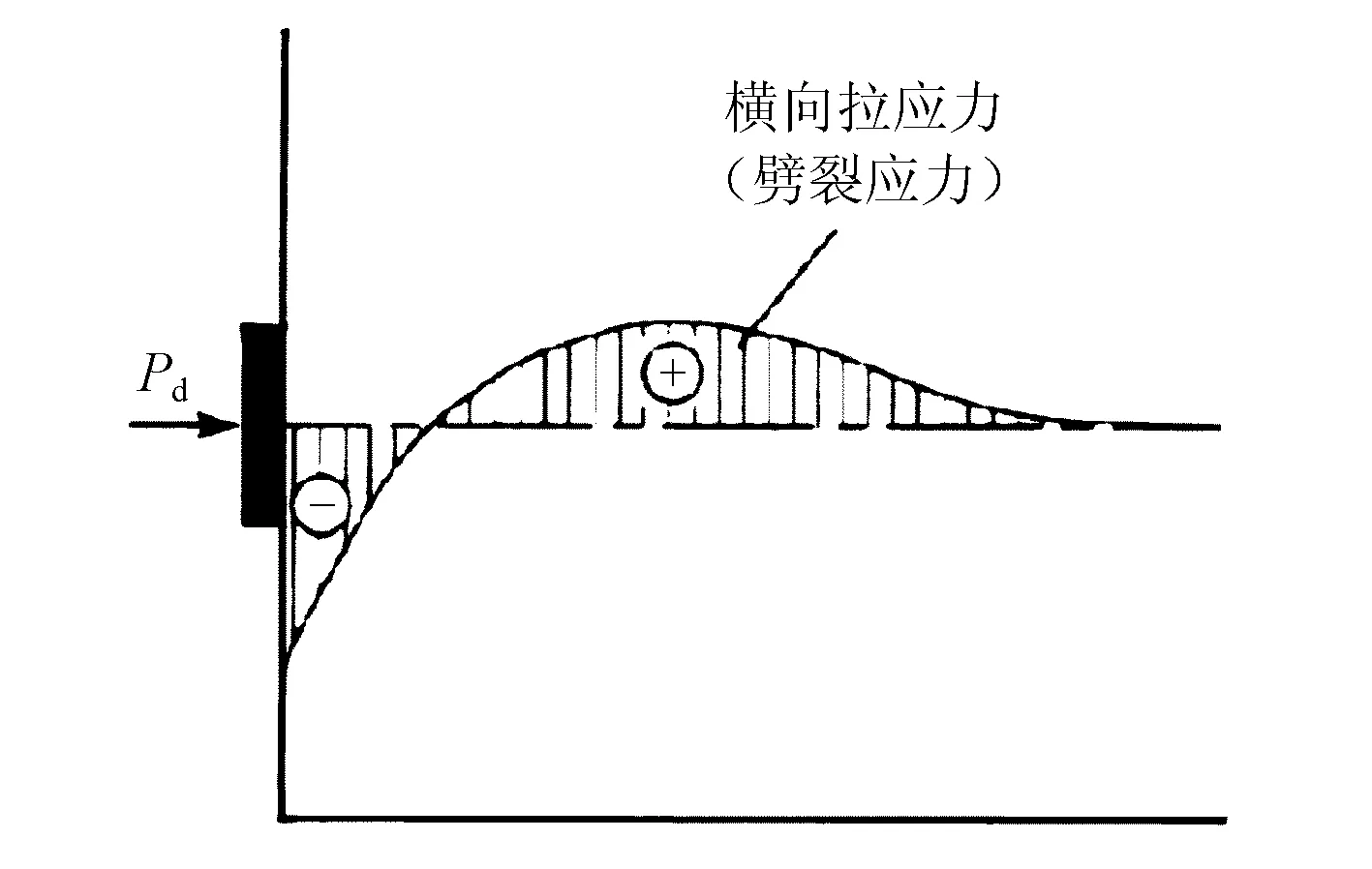
图3 锚下劈裂应力分布图

式(2)考虑了锚头偏心布置、钢束下弯角度这2个因素，采用拉压杆分析模型，具有较好的适用性。

3.3 工程实例计算

本文选取4号块段，运用简化计算公式进行计算。

3.3.1抗劈裂验算

选取边腹板作为计算对象，腹板束预应力为2束15-15.2，张拉控制应力0.72fpk=1 339.2 MPa，锚垫板尺寸取a=265 mm，预应力下弯角度取25°，腹板高度h=5 424 mm，锚头偏心距e=1 696 mm。故

Pd=1.2×1 339.2×15×2×139=6 669 832 N

Tb,d=0.25×6 669 832×(1+0.63)2×

(1 444 322+1 410 669) N=2 855 kN

db=0.5×(5 424-2×1 696)+

1 696×0.423db=1 733 mm

腹板配置抗劈裂箍筋，HRB400钢筋，直径20 mm，间距10 cm，配置范围为2db。

计算γ0Tb,d≤fsdAs，验算拉杆承载力是否满足要求。

γ0Tb,d=1.1×2 855=3 140.5 kN。

fsdAs=330×3.141 59×100×68 N=7 050 kN。

通过计算，利用拉压杆模型计算预应力锚下劈裂力，抗劈裂力承载力满足要求。

3.3.2最大劈裂应力计算

上述计算中，已经计算出了劈裂力的合力大小及合力作用位置。通过拉压杆模型，可以很方便地进行承载力验算，出于偏安全考虑，预应力锚固力采用了1.2倍张拉控制力，为了较为准确地计算劈裂应力，本文中的劈裂应力并未考虑1.2的安全系数。

根据式(1)的计算原理，最大应力与平均应力存在一个比值关系，文献[2]给出了比值的范围，通过实验分析得到该比值大致为2。

4号块腹板宽度800 mm，预应力孔道内径100 mm，取劈裂截面水平长度为2db=3 466 mm抵抗劈裂力的截面应扣除预应力管道面积，并应考虑钢束下弯角度的影响。

经过计算，发现锚下确实存在较大的劈裂拉应力，但未超过C50混凝土抗拉强度标准值2.65 MPa。

4 ANSYS实体模型分析

为进一步分析锚下局部应力情况，与上文中的简化公式计算结果进行对比，同样选取了4号块建立实体模型，进行局部分析。混凝土采用SOLID65单元，弹性模量34 500 MPa，泊松比采用0.2。模型考虑了预应力孔道内径10 cm。因裂缝出现在张拉后、灌浆前，此时钢束在直线段可认为未与结构接触，预应力锚固力通过锚头传递到整个结构。故锚固力采用锚头荷载加载(扣除预应力损失后的有效锚固力)，未模拟预应力单元。张拉时，块段支撑于底模上，不考虑结构自重作用。三维有限元分析模型见图4。

图4 三维有限元分析模型

主拉应力云图见图5。锚下劈裂区腹板最大主拉应力为2.1 MPa。与上文简化计算最大拉应力2.28 MPa较为接近。简化计算公式具有一定的实用性。

图5 主拉应力云图(单位：MPa)

5 裂缝控制措施

5.1 增加抗劈裂配筋

本文拟通过抗劈裂钢筋应力进一步量化裂缝宽度，即通过控制钢筋应力有效避免裂缝产生或者减小裂缝宽度。参考文献[1]中裂缝宽度的计算公式见式(4)、式(5)。

(4)

(5)

式中：Wcr为裂缝宽度，mm；C1为钢筋表面形状系数；C2为长期效应影响系数；C3为受力性质系数；σss为钢筋应力，MPa；c为保护层厚度，mm；d为钢筋直径，mm；ρte为有效配筋率。

以此方法验算4号块在锚下劈裂力作用下，钢筋应力及裂缝宽度。

Wcr=0.14 mm

根据第三方的检测结果，现场实测4号块最大裂缝宽度为0.12 mm，这与计算结果较为接近。文献[1]中提到，采用式(2)进行抗劈裂配筋设计时，美国德克萨斯大学100余个试件和中国建筑科学研究院50余个试件的裂缝情况均能得到很好地控制，裂缝宽度不超过0.15 mm。这与式(4)、式(5)的计算结果接近。

通过将文献[1-2]的试验研究数据与本工程的第三方现场检测结果进行对比，发现上述简化计算公式所得结果均较为接近。用上述方法进行抗劈裂配筋设计具有一定的可靠性。

5.2 优先张拉竖向预应力

大跨度桥梁一般设计为三向预应力，竖向预应力可采用精轧螺纹钢或预应力钢绞线施加。通过施加竖向预应力，使结构获得竖向压应力，可以有效地减小主拉应力，从而避免混凝土开裂。竖向预应力是控制此类劈裂裂缝最有效、最简单的方法，其原理清晰，设计施工成熟简单。但实际工程中，三向预应力结构往往也会出现劈裂裂缝，这是由于预应力张拉顺序造成的。本文建议挂篮施工桥梁均应采取：顶板→竖向→腹板预应力的最佳张拉顺序，并按式(6)计算施加。

(6)

式中：σtp为混凝土主拉应力，MPa；σcx为法向压应力，MPa；σcy为竖向压应力，MPa；τ为剪应力，MPa。

由式(6)可知，施加竖向预应力即增大σcy，可减小主拉应力。

本工程实例在7号节段进行了预应力束张拉顺序调整，为了揭示此措施对控制裂缝的效果，边跨下游边腹板和中跨上游边腹板未施加竖向预应力。张拉后裂缝开展情况见表1。

表1 调整张拉顺序腹板裂缝

由表2可知，先张拉竖向预应力能够有效地抑制裂缝的开展。

5.3 提高施工质量

施工过程中，养护龄期达不到设计要求，混凝土强度和弹性模量过低，过早地张拉预应力均会导致混凝土开裂[5]。另外，施工时应加强预应力管道定位，防止管道因浇筑振捣出现偏位。混凝土浇筑后应严格进行覆盖浇水养护。在本工程实例中，5号节段在采取了加强定位、加强养护、龄期>10 d进行张拉的措施后，虽然出现了裂缝，但较未采取任何措施的4号节段，开裂情况明显改善。