基于粒子群算法的工业机器人智能打磨轨迹问题研究
2020-12-23葛为民程德响
刘 帅,葛为民,程德响
(1.天津理工大学机械工程学院 天津市先进机电系统设计与智能控制重点实验室 机电工程国家级实验教学示范中心,天津300384;2.南开大学数学科学学院,天津300071)
工业机器人目前在生产制造领域中应用广泛,如船体焊接,港口大构件打磨,汽车零部件焊接及装配等,具有高度的重复性,所以合理的加工轨迹规划能够提高生产效率,并且在实际生产中,还需要考虑刀具的磨损和机器人避障问题,所以为了在满足打磨工艺要求的前提下提高工业机器人的轨迹质量,提出了一种基于粒子群算法的打磨系统.通过视觉系统对焊接工件进行图像采集,导入数据库进行分析得出打磨工艺决策并建立适应度函数.应用粒子群优化算法(PSO),对多目标进行优化,使得整个打磨轨迹满足时间短、轨迹平滑、具有较好的避障性且能满足打磨工艺要求.Jun Liu和Tianyun Shi[1]提出了通过合作与竞争的粒子群优化算法对无人机在三维空间的轨迹进行了优化,采用分而治之的方式,有效的缩小了问题的维数,合理的规划了无人机规避雷达轨迹以及无人机之间的碰撞.李丽等[2]利用NURBS曲线对关节位置点进行插值,提出自适应指数罚函数处理约束问题,通过骨干粒子群优化算法寻求最优解,得到了较为平滑且轨迹误差相对较小的轨迹.徐海黎等[3]通过三次多项式曲线去关节关键点进行连接,采用免疫克隆算法对构造函数进行优化,得到时间和能量二者平衡优化的轨迹.靳岚等[4]到利用三次B样条曲线对机器人连续路径进行规划,缓解了运动过程中突变问题.许曦[5]等对奇异性规避进行分析,在满足运动学约束的条件下,对机器人基座位置进行优化以提高焊接精度.王玉宝等[6]采用动态学习因子进行高次多项式插值进行时间最优规划.浦玉学等[7]从时间和能耗入手基于引力搜索算法和贪婪选择策略,得到了光滑且连续的轨迹曲线.
目前针对该问题的研究大多是单纯的对机器人的运动约束建立适应度函数,但轨迹规划是基于工艺要求而产生的,对其优化的目的也是为了提高工艺性能.本文依托于中汽车零件焊缝缺陷打磨项目,搭建了焊接打磨系统,设计了一套较为良好的打磨轨迹规划方案.
1 系统组成
1.1 总体设计
基于ABB-IRB-2600和新松SR50的焊接打磨系统,主要包括工业机器人系统、单目工业相机、三自由度滑台、上位机、安全保护装置以及控制系统(包括PLC控制柜、HMI以及操作按钮盒).工作站环境布局如图1.为了贴近实际生产,本文选择和汽车零件相同材料的Q235板材,选用恒力打磨头,根据相机识别的焊缝缺陷类别选择较为合适的打磨工艺进行打磨.
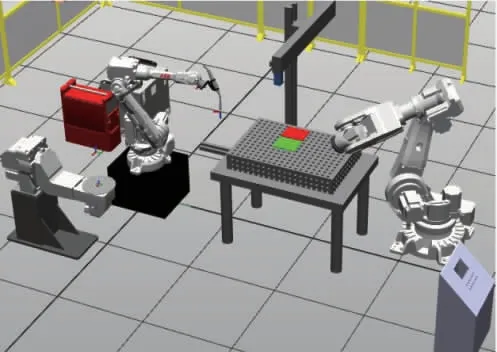
图1工作站环境布局Fig.1 Workstation environment layout+
1.2 通讯及控制系统
图2为控制系统流程图,PLC为整个控制系统的数据管理中枢,上位机Visual Studio窗体应用程序为主控者,对焊缝缺陷进行采集分析以及工艺决策.各个设备之间通过TCP/IP进行通讯,数据以1024byte进行通讯,从而进行位置信息、启停状态、图像分析结果等信息交互.

图2控制系统流程Fig.2 Control system flow chart
1.3 视觉采集系统
视频采集系统由CMOS相机、LED光源和SINA MICSV90伺服驱动器控制的三自由度滑台组成.本文选用的CMOS相机为DMK Z30GP031黑白变焦相机,相机接口为GigE,可以人工调整焦距、光圈、捕获帧速率和捕获图像分辨率.将工作台划分成多个固定工位,通过人工调试对采集效果良好的滑台位置进行示教,等待ABB机器人焊接完成指示信号,进行图像采集和分析,并反馈给VS窗体应用程序中的决策系统.
2 焊缝缺陷位置提取
焊缝缺陷是打磨机器人运动的目标点,因此计算焊缝缺陷在打磨机器人基坐标系的位置至关重要,其本质问题是计算图像中的焊缝缺陷像素在打磨机器人在基坐标系下的位置.本文主要使用两个步骤计算焊缝缺陷位置,第一步是计算焊缝缺陷像素在工作台坐标系下的位置,第二步是根据工作台坐标系与打磨机器人基坐标系的转换关系计算焊缝缺陷像素在打磨机器人基坐标系下的位置.定义四个必需的坐标系,分别为打磨机器人基坐标系(Xγ,Yγ,Zγ),工作台坐标系(Xω,Yω,Zω),行走十字机构平面运动坐标系(Xm,Ym)和成像平面坐标系(U,V),如图3所示.将相机捕获图像的中心点聚焦于工作坐标系原点,即相机的光轴与工作台坐标系的Zω轴重合,将此位置设置为行走十字机构平面运动坐标系的原点.因此,行走十字机构的位置(xm,ym)就是相机光轴在工作台平台坐标系的位置.

图3坐标转换Fig.3 Coordinate conversion
根据像素的位置(u,v)和像素所代表的实际距离d可计算像素在工作台平面坐标系下的位置(xω,yω,zω)如下

其中,d可以通过张正友相机标定得到;zω=0的原因是焊缝位于工作台表面.通过计算打磨机器人基坐标系和工作台坐标系得到转换矩阵.
3 轨迹规划
3.1 避障及问题描述
在静态环境下,已知障碍物分布不变,规划一条满足目标约束且时间最短的轨迹.参考文献[8]基于自身环境建模如图4所示物体为已做膨化处理的障碍物,记起点坐标为S(xS,yS,zS),终点坐标为E(xe,ye,ze)优化的最终路径为Path(S,P1,P2,…,Pn,E).
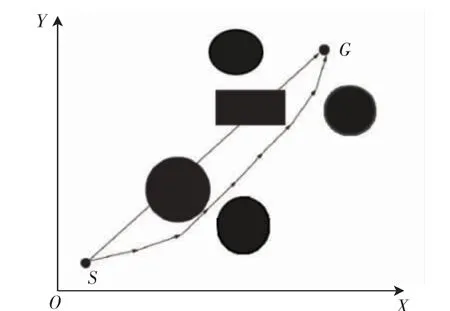
图4避障轨迹示意图Fig.4 Schematic diagram of obstacle avoidance trajectory
为了有效减少同时规划多个维度的复杂度,将三维优化问题进行了一定的转化[8],先不考虑Z轴方向转而处理二维平面空间,并将进行了降维处理.如图连接起点和终点,作N条垂直于SE的直线且将SE分成N份,对任意第i个点x方向的坐标值可表示公式(1)形式,这样问题就变成了对X方向坐标值以及n值进行优化.

为了方便计算,以S为坐标原点,SE向量作为X轴正方向.根据右手定则确定Y轴,建立新的坐标系O′X′Y′,假设新旧坐标之间的夹角为α,则两坐标系之间的坐标变换公式(2)

3.2 运动学模型
轨迹规划既可以在直角坐标空间也可以在关节空间中进行,在焊缝的打磨过程中,机器人的稳定性对打磨工艺有很大影响,同时在打磨过程中,不同的焊缝缺陷对机器人磨削角度也不同.因此需要考虑到机器人在运动过程中关节速度值、关节加速度值、关节二次加速度值以及机器人的位姿等问题.所以本文以关节空间为基础对轨迹进行规划.
施工管理费用控制过程中,一方面,要分析施工管理费用阶段性规划的形成,需要在前期总体管理费用规划形成基础上,结合实际工程建设状况、工程建设规模和工程建设工期等方面,将费用进行细致化划分,制定阶段性费用管理目标,在目标指引下,保证阶段性管理费用向着精细化的方向落实;另一方面,加强管理费用使用审批和监督管理,严格每一项管理费用产生的审批程序,做好现实核查和追踪检查工作,对管理费用流动实现动态化、实时化的监督。
3.3 轨迹插值
本文轨迹共分为两个部分,一是寻迹空间轨迹,一个是任务空间轨迹.在机器人轨迹规划中,其优劣程度由适应度函数来衡量,影响因素如时间、能量损耗、轨迹平滑程度、工艺性能等.考虑到工艺质量和加工效率因素,本文主要对时间、轨迹平滑程度以及工艺性能三方面展开研究.
根据前文避障和轨迹生成小节得到了在笛卡尔空间坐标系中N+2个关键点坐标值,根据机器人逆运动学方程可求出机器人在关节空间中的关键点序列,为了保证加加速度稳定,可通过一系列五次多项式曲线来连接这些关键点[9].对于任意关节r,q1,q2,…,qn为其关节空间的关键点,t1,t2,…,tn是对应的时间节点.定义Qi(t)为时间间隔[ti,ti+1]内的五次多项式函数分别为关节空间中关键点qi和qi+1之间的位移、速度、加速度和二次加速度.已知机器人初始时刻和终止时刻的关节速度值和加速度值.根据五次多项式有

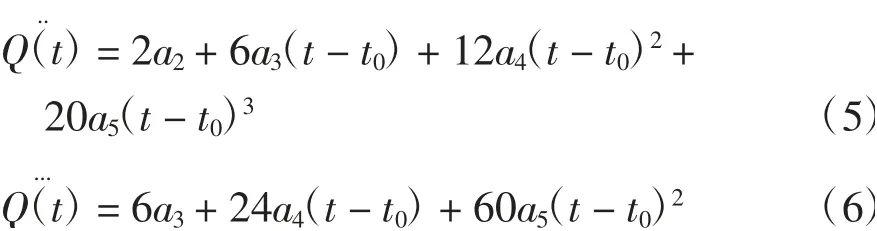
本文轨迹共分为两个部分,一是寻迹空间轨迹,已知任一段轨迹,t0为起始点,tf为终止点,则

工艺需求设定上述6个变量的值,带入公式(3)、(4)、(5)中联立求得式(3)中各项式系数,进而可求得该关节任意时刻的关节角位移、角速度、角加速度和二次加速度,作为后续适应度函数中约束判断的依据.
4 机器人轨迹多目标优化
4.1 约束条件
为了保证机器人在工作的时候稳定运行,提高安全性能和机器人的使用寿命,需要对其关节进行物理极限约束。
关节速度值

关节加速度值


式中vmax、amax、jmax分别为关节j的速度、加速度、二次加速度的约束.

对于避障问题,以障碍物圆心到弦的垂直距离公式(11)作为是否该条轨迹存在碰撞的依据其中,di,max表示第i段轨迹分别与所有障碍物的最小垂直距离;rmax表示障碍物的半径与打磨头最大半径之和;M表示障碍物的圆心;Pi和Pi+1为第i段位移的初始和末端位置坐标.
4.2 适应度函数
适应度函数的建立依赖于优化目标,得到的轨迹好坏取决于目标函数的形式.本文旨在得到一条高效、具备较好的工艺性能和安全性能的轨迹,建立的适应度函数公式(12).
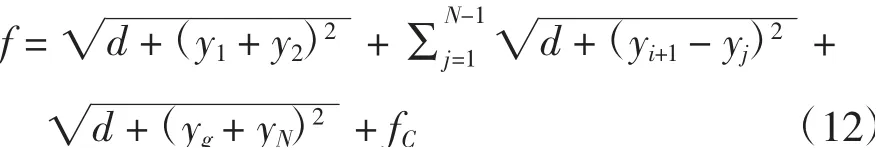
式中,d=((xe-xS)/(N+1))2是一个定值;fC初始值设置为0,粒子需满足约束(11).
根据式(13)规划出的关键点,进行二次粒子群优化式(14),并将优化的适应度值反馈给适应度函数f

式中,hi为路径点pi到pi+1的时间间隔.为了更好的引导粒子,参考文献[10-11]引入了自适应指数罚函数来处理罚函数问题.
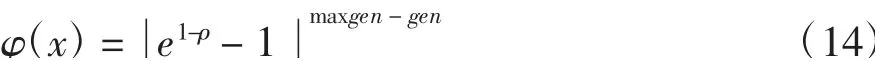
其中,gen为迭代次数;ρ为单个粒子中各段轨迹可行解的比例,0≤ρ≤1.
该罚函数优点在于优化前期,惩罚系数较大,粒子的探索能力较好;优化后期惩罚系数较小,提高了粒子的开发能力.因此新的适应度函数

λ1、λ2分别为时间系数和惩罚系数,用于平衡最有时间规划和惩罚程度在整个优化过程中,通过调整二者的值可使机器人运动总时间和工艺性能在某种程度上均达到最优.
在Matlab中编程对新的适应度函数进行优化,具体算法流程如图5.
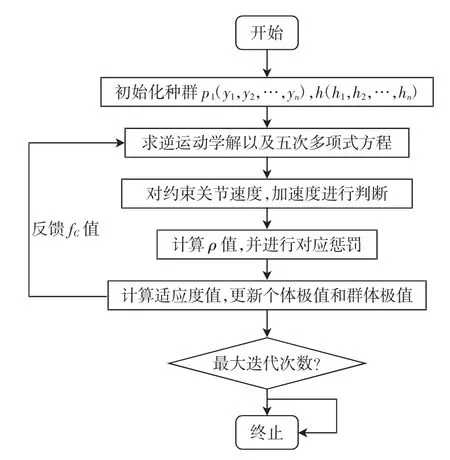
图5基本粒子群算法流程图Fig.5 Flow chart of elementary PSO
5 实验结果及分析
对于打磨姿态,在起始点时已经设定好,只对其位置进行优化分析,而机器人只有前三个轴控制末端执行器位置,因此本文只对新松机器人关节1、2、3轴进行了分析.起始点S和目标点E坐标值分别为(733,-557,476),(931,-796,476);根据3.1小节得到的一组插值点见表1,借助Matlab中ikine函数把笛卡尔空间坐标转换成关节空间坐标求出各关节角度见表2,总运行时间为14.6 s.对于多节点轨迹的五次多项式系数求解方法请参考文献[12],本文不多赘述.利用粒子群算法对适应度函数以及目标约束进行分析得出最优解,由于篇幅有限,本文只展示了轴3的最优解如图6所示,最优群体适应度值如图7所示,其中粒子最大迭代次数maxgen设置为20,种群粒子数目sizepop值为±10,最大关节角速度MaxAgVel值为±12,最大关节角加速度MaxAgAcc值为±9.
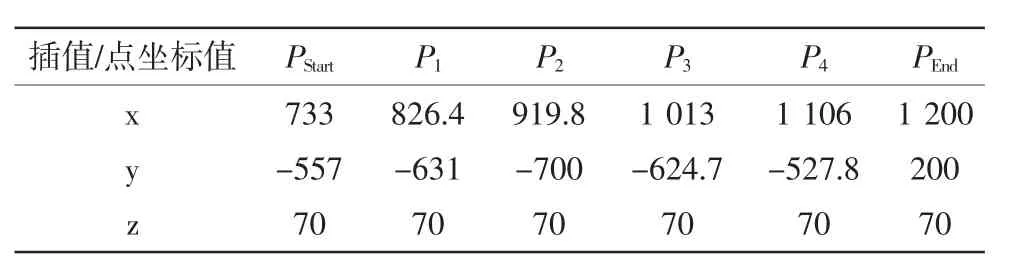
表1插值坐标点值Tab.1 Interpolate coordinate point values

表2各轨迹段所用时间Tab.2 The time taken for each trajectory segment
工作环境中障碍物相对于机器人基坐标系Obs1=[896.2,-806.7],Obs2=[1 000,200].最优轨迹中任意点距离障碍物最小距离为612.346 1满足约束.


图6关节轴3最优轨迹角度、角速度和角加速度曲线图Fig.6 Optimal trajectory angle,angular velocity and angular acceleration curves of joint axis 3

图7最优群体适应度值Fig.7 Optimum population fitness value
6 结论
从上述研究可以到看到粒子在第9代就达到最优,收敛较快,虽然最优解满足约束,但可能会陷入局部最优解,且算法运行较慢,因此程序在精度满足要求的前提下还需改进以提高运行速度进而适应实时性要求较高的场合.
