《长方形周长与面积关系》教学设计

◇（江苏：丹阳市访仙中心小学）

教学内容

小学数学国标本苏教版三年级下册第75 页《探究长方形周长与面积关系》的习题课教学。

教学目标

——通过围周长相等、面积不等，面积相等、周长不等的长方形的具体操作，探究“长方形周长相等时，长、宽与面积之间的关系，长方形面积相等时，长、宽与周长之间的关系”。

——在主动探索、交流的过程中，尝试用枚举、列表的方法探究规律，加深对长方形周长、面积概念的理解，熟练长方形（包括正方形）周长和面积的计算。

——让学生在动手操作的活动中，体会有序思考及数形结合的思想。

教学重点

通过探究长方形形状的变化引起周长与面积的变化规律，培养学生良好的观察、操作、抽象、概括能力以及思考、解决实际问题的能力。

教学难点

探究长方形周长相等时，长、宽与面积之间的关系；长方形面积相等时，长、宽与周长之间的关系。

教学过程

一、复习铺垫，提出问题

说出面积和周长：长方形长7 厘米，宽3厘米；长方形长8厘米，宽2厘米。

对于这两道题你有什么发现或有什么想法？

【意图：让学生初步感悟到，长方形周长相等，面积不一定相等，并诱发思考：长方形周长相等，面积的大小与长方形的长与宽到底有什么关系？】

二、提供材料，分组探究

（一）大胆猜想：长方形周长相等，面积的大小与长方形的长与宽到底有什么关系？

（二）如何验证？

（三）6 人小组讨论：提供小棒和方格纸，让学生分组讨论。

方法一：用20 根小棒围成各种长方形，面积是多少？与长方形的长与宽到底有什么关系？

方法二：在方格纸上画出周长是20 厘米的不同长方形， 面积是多少？与长方形的长与宽到底有什么关系？（每个方格表示1平方厘米）

方法三：列表计算，周长是20厘米的不同长方形， 面积是多少？与长方形的长与宽到底有什么关系？①分组操作并探究。②分组讨论交流。

（四）大组交流

1.方法一、二

2.引导填表

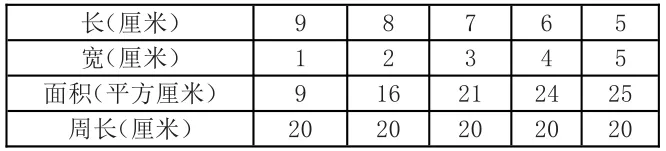
长（厘米）宽（厘米）面积（平方厘米）周长（厘米）9 1 9 2 0 8 2 1 6 7 3 2 1 6 4 2 4 5 5 2 5 20 20 20 20

师：你觉得这组数据应该怎样排列？为什么？（有序排列，做到不重不漏，而且便于发现规律。）

【意图：提供材料，让学生分组讨论，进行操作验证，让学生感悟到，得出正确的结论一定要想方设法加以验证，在验证中尽量有序列举，便于发现规律。】

三、观察比较，得出结论

（一）师：大家再来观察一下表中数据，你发现什么规律吗？周长相等时，长与宽越接近面积越大。当围成的长方形长为5，宽为5 时，即长与宽相差数最小时，这个长方形面积最大。

（二）想一想：周长相等时，为什么长与宽越接近面积越大？

（课件演示方法二：当长减少1厘米时，面积就相当于减少1 平方厘米，当宽增加1厘米时，面积就相当于增加10平方厘米，实际就增加了多少平方厘米？以此类推。明白了吗？当我们得出一个结论的时候，还要深入思考为什么会有这样的结论。）

（三）是不是周长相等时，所有长方形的长与宽越接近面积都越大？

（四）怎么办？验证？怎么验证？（再举一些正例或反例）

（五）小结：那你现在有什么明确的结论？长方形周长相等时，长与宽越接近面积就越大。（板书）千金难买回头看：我们回过头来思考，我们是怎么样提出问题、进行验证、得出结论的？

【提出问题—进行验证（正例或反例）—得出结论】

在这一过程中要提醒学生什么？（有序，提出问题很重要。）

提出一个问题往往比解决一个问题更重要，因为解决问题也许仅仅是一个教学上或实验上的技能而已。而提出新的问题新的可能性，从新的角度去看旧的问题，都需要有创造性的想象力，而且标志着科学的真正进步。——爱因斯坦

【意图：数形结合，便于将复杂的问题简单化，便于学生更加深入理解验证的结论。回顾小结：让学生学会自己去发现问题，提出猜想，进行验证，获得结论，从而解决问题，使学生乐于学习，学会学习，达到了教是为了不教的目的。】

四、自主探究，拓展延伸

（一）既然提出问题很重要，你还有什么问题要提？

（二）长方形面积相等，周长和长与宽有什么关系？

（三）你想如何来研究这个问题？

（四）6 人小组合作，自主探究，得出结论。

方法一：在方格纸上画出所有面积是16 平方厘米的长方形，算出它们的周长，思考周长和长与宽有什么关系？（课件演示出结果）

方法二：列表计算，面积是16平方厘米的长方形的周长，思考周长和长与宽有什么关系？

长（厘米）16宽（厘米）8 4 1 2 4面积（平方厘米）16 16 16周长（厘米）34 20 16

（五）面积相等时，长与宽越接近周长越小。（举其他正例或反例）

（六）小结

【意图：让学生独立提出猜想，进行验证，获得结论，从而解决问题；进一步学会用枚举、列表的方法探究规律，加深对长方形周长、面积概念的理解，熟练长方形周长和面积的计算；体会有序思考及数形结合的思想。】

五、运用规律，解决问题

（一）用长28分米的绳子围成长方形或正方形，怎样围图形的面积最大？最大面积是多少？

（二）一个用竹篱笆围成的长方形养鸡场，长12 米，宽8 米，现在要进行扩建，你能在不增加材料的情况下增加养鸡场面积吗？最多能增加多少面积？

【意图：在实际应用中，加深对规律的认识与理解，促进认知结构的建立与完善。】

六、课堂小结，反思评价

通过今天的学习，你有什么收获？

（一）当周长一定时，长方形的长与宽越接近面积越大。

（二）当面积一定时，长方形的长与宽越接近周长越小。

七、结论

本节课通过围周长相等、面积不等，面积相等、周长不等的长方形的具体操作，尝试用枚举、列表的方法探究“长方形周长相等时，长、宽与面积之间的关系，长方形面积相等时，长、宽与周长之间的关系”，加深对长方形周长、面积概念的理解，熟练长方形周长和面积的计算，体会有序思考及数形结合的思想。培养学生良好的观察、操作、抽象、概括能力以及提出问题、解决实际问题的能力。■