基于AHP 灰色统计下的共享汽车问题分析与研究

孙盼盼；何庆；徐丹

（①铜陵学院数学与计算机学院，铜陵244002；②铜陵学院建筑工程学院，铜陵244002）

0 引言

近年来，共享汽车作为公共交通中的一种新型的交通工具，在各个城市中不断涌现，逐渐出现在人们的视野。现如今，全球有数百家企业正提供着有关共享汽车的服务，数万辆共享汽车正服务着数百万用户，可以说共享汽车的浪潮已经来临[1]。而对不同城市的共享汽车发展状况做出评估，能够很好的反映出共享汽车在我国不同地区城市中的发展状况，从发展状况中能够更好的看出共享汽车在我国未来的发展趋势。

文章通过随机选取一线城市中的北京、上海；新一线城市中的重庆、天津；二线城市中的济南、合肥这六个城市作为研究对象，分别对这六个城市的社会经济发展水平、交通运输发展水平、共享汽车市场发展水平、企业发展可行性这几个层面的不同影响因素做出统计分析，来探讨共享汽车的发展水平，从而可以根据此方法来研究其他城市中已试行或未实行共享汽车的城市发展状况或发展趋势。

在所选取影响城市共享汽车发展状况的四个主要影响层面中，每个层面中都有对应着的不同影响因素，可见城市共享汽车发展系统是一个较为复杂的系统。其中各个层面中的影响因素既有已知信息，又有未知信息，且所选取的样本数据不够多，因此城市共享汽车发展系统可视为一个典型的少样本、贫信息的灰色系统[2]，而灰色统计法就是以这种“小样本”、“贫信息”不确定性系统为研究对象的；同时文章中的城市发展状况评估又是一个多层次的评价系统，通过结合层次分析法（AHP）与灰色统计法各自的特点，构建出基于AHP 的灰色统计模型，运用此模型能够很好的对我国不同城市的共享汽车发展状况做出评估。

1 研究方法

层次分析法（Analytic Hierarchy Process，简称 AHP 法）是一种简便、灵活而又实用的多准则决策方法。按照问题的性质以及问题的总目标，先把问题分解为不同的组成因素，并按照各个因素间的相互关系，将其分解为不同的层次结构，再按照求解判断矩阵特征向量的办法，求得每个层次中各个元素的权重，从而形成一个多层次的分析结构模型。

灰色统计法是以“部分信息已知，部分信息未知”的“小样本”、“贫信息”不确定性系统为研究对象，通过对“部分”已知信息的生成、开发，提取有价值的信息，实现对系统运行规律的正确描述和有效控制。

文章中针对评估对象的层次结构及指标权重所运用的方法就是层次分析法（AHP），模型中各个指标的量化以及比较则是通过灰色统计法中的灰数和白化权函数来确定的。

2 实证研究

2.1 递阶层次结构的确立

城市共享汽车发展状况涉及多层次多方面的因素影响，通过查阅相关资料，我们可以将影响城市共享汽车发展状况的主要指标归结为4 大方面12 个因素，其中“城市共享汽车发展状况”为最高层，即作为综合评价目标层；中间层U 层作为约束层（准则层）代表影响城市共享汽车发展情况所涉及的中间环节；最底层V 层表示影响城市共享汽车发展状况的具体指标因素。具体层次结构模型如图1。

同时可将二级评价指标记为Us（s=1，2，…，q），其中U代表二级评价指标所组成是集合，记为U={U1，U2，…，Uq}；Vs（s=1，2，…，q）代表三级评价指标Vsi（i=1，2，…，n）所组成的集合，记为Vs（Vs1，Vs2，…，Vsn）。

2.2 指标权重的确立

图1 城市共享汽车发展状况的层次结构模型

层次分析法确定权重有多种方式，如：和法、根法、特征根法、和对数最小二乘法等等，此处选择确定指标权重的方法为特征根法。具体过程如下：首先，依据问题中各个因素间的关系建立问题的递阶层次结构；其次，对同一层次的各因素关于上一层次中其一准则的重要性进行两两比较来构造两两比较的判断矩阵；最后由判断矩阵计算并比较因素对于该准则的相对权重，再进行判断矩阵的一致性检验（该过程可在MATLAB 中进行）。若通过一致性检验，则可直接输出特征向量，即所需求得的指标权重；若没有通过一致性检验，可通过调整判断矩阵直至通过一致性检验。通过MATLAB 计算，可得城市共享汽车发展状况的评价指标及权重表如表1 所示。

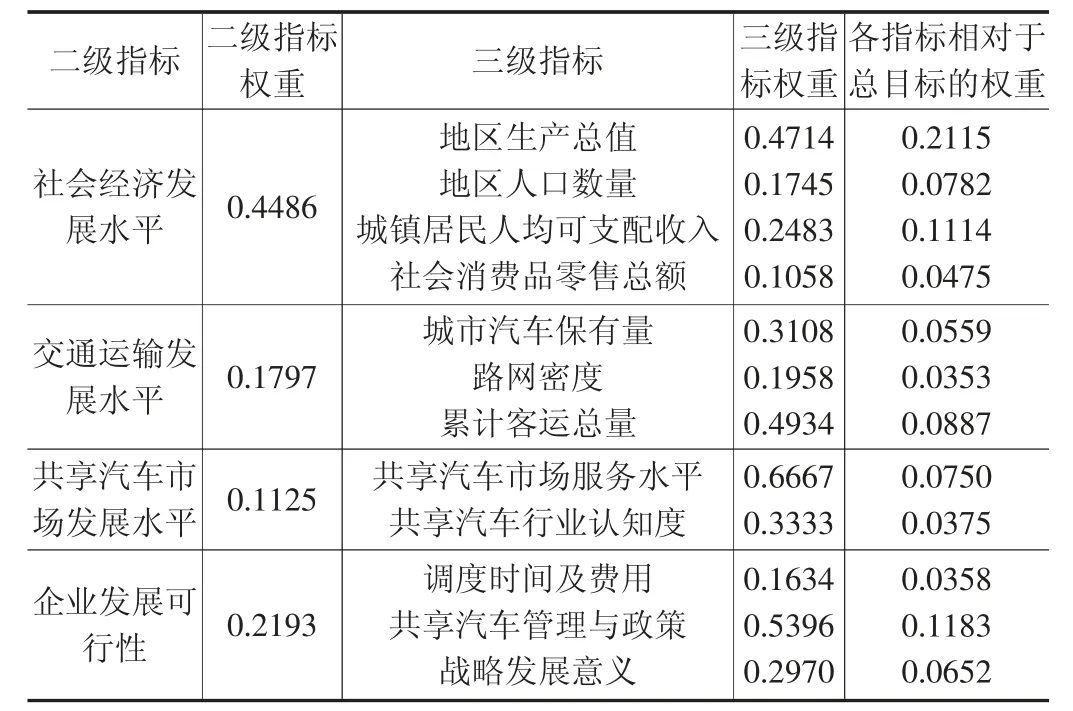
表1 城市共享汽车发展状况各指标权重

即二级评价指标Us对应的权重向量

三级评价指标V1i所对应的权重向量

三级评价指标V2i所对应的权重向量

三级评价指标V3i所对应的权重向量

三级评价指标V4i所对应的权重向量

2.3 样本指标体系及指标权数统计

通过查阅相关资料，确定了以上的二级指标、三级指标作为影响城市共享汽车发展状况的指标因素。由此，可根据查阅国家统计局、各城市统计年鉴、中华人民共和国交通运输部中2019 年度的相关统计结果，提取出对应的指标数据，分别对定量指标做无量纲标准化处理，对定性指标量化处理后，可得北京、上海、重庆、天津、济南、合肥这六个城市处理后的具体数值，处理结果见表2。

可设M 城市的评价矩阵为D（M）：

则由以上数据可得：

2.4 确定评价灰类

确定评价灰类就是要确定评价灰类的等级数、灰类的灰数及灰数的白化函数，视实际评价问题分析确定。文章将评价灰类划分为4 个等级，设评估灰类序号为e，即e=1、2、3、4，其对应的评估灰类等级依次为：很好、好、一般、不好。相应的评价灰类的白化权函数如图2 所示。

2.5 计算灰色评价系数

在所得M 城市的评价矩阵D（M）中，以第一个城市北京为例，计算其灰色评价系数。可假设 D（北京）=D（1），则有

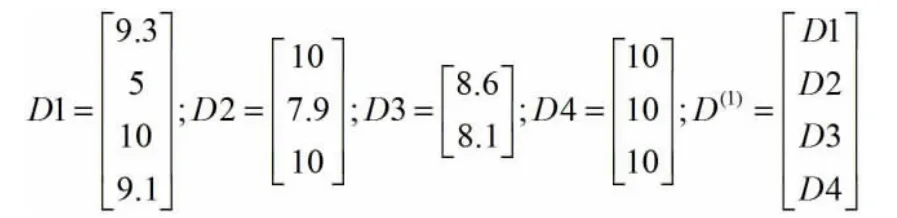
关于评价指标Vsi，M 城市属于第e 个评价的灰类灰色评价系数可记为：

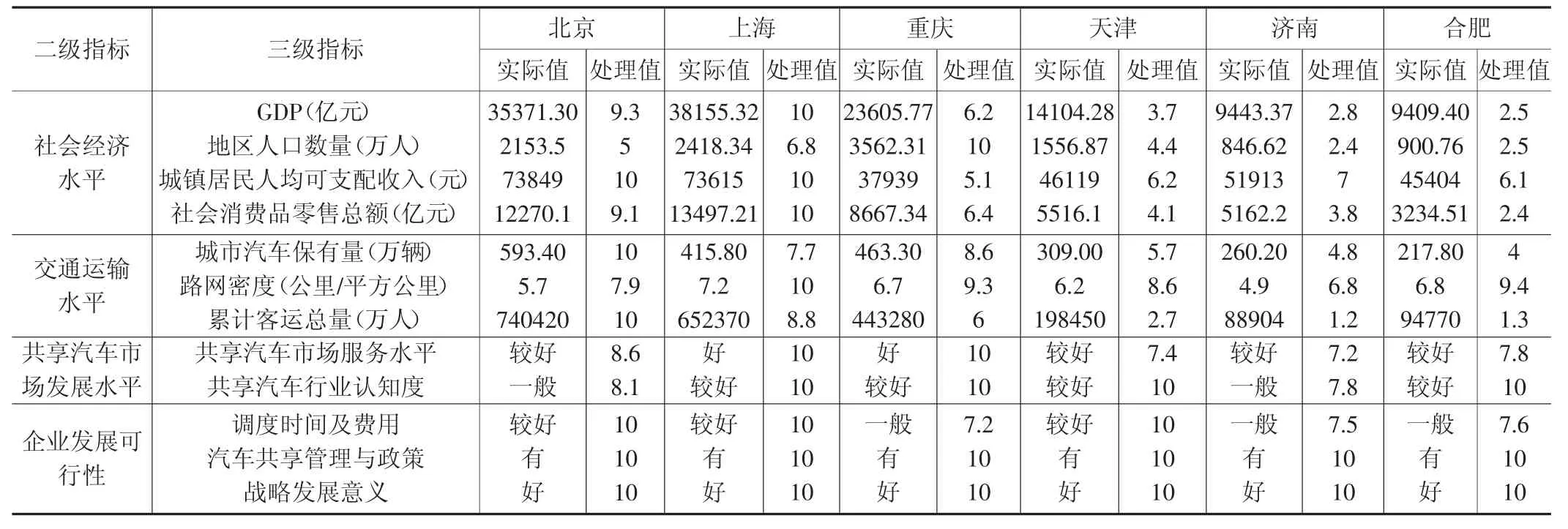
表2 2019 年度城市主要指标值及处理值

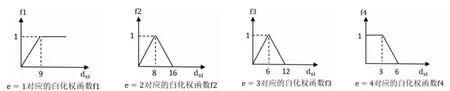
图2 各评价灰类所对应的白化权函数图像

各个评价灰类的总灰色评价系数可记为XMi，且有：

则由公式（1）、公式（2）可计算城市北京的灰色评价系数，对于评价指标属于第e 个的评价灰类的灰色评价系数X11e为：

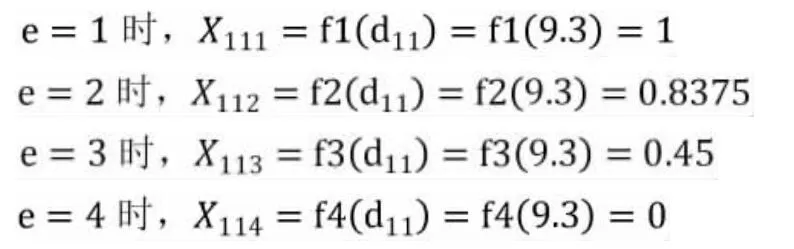
则各个评价灰类的总灰色评价系数X11为：

2.6 计算灰色评价权向量、灰色评价权矩阵

对于评价指标Vsi，M 城市属于第e 个评价灰类的灰色评价权向量记为rMi：

综合这些权向量可以计算出灰色评价权矩阵：

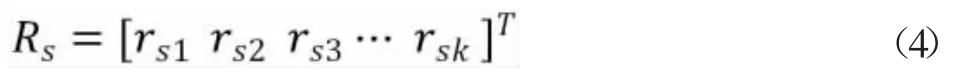
则由公式（3）、公式（4）可计算出北京的评价指标V11所对应的灰色评价权向量r11：

即：

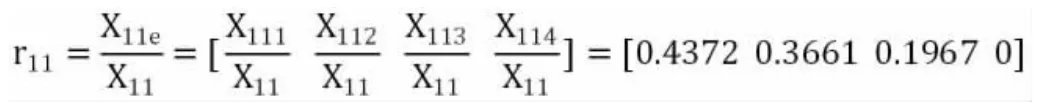
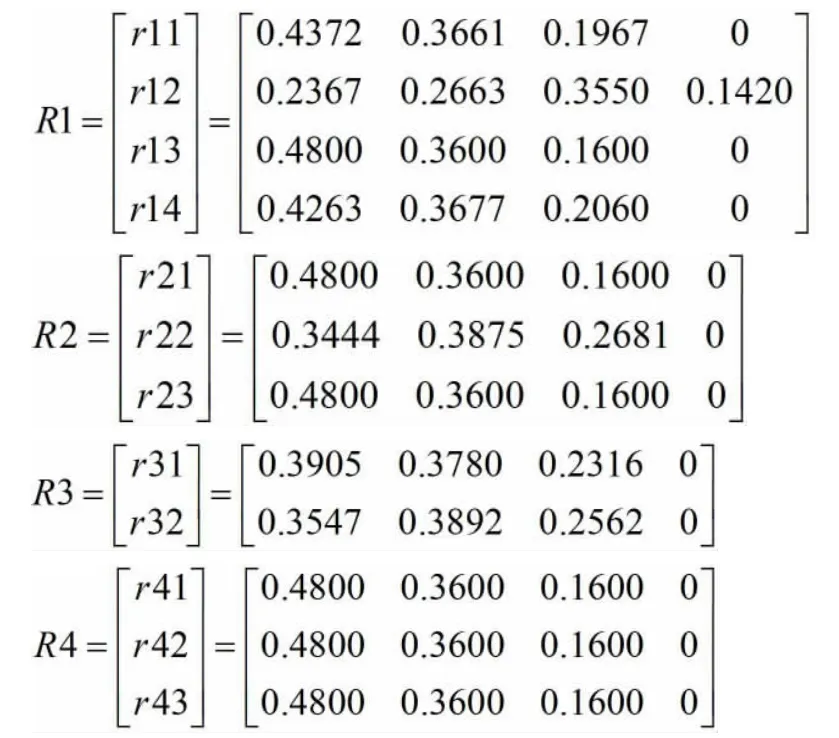
同理可得北京的其他灰色评价权向量 r12、r13、r14、r21、r22、r23、r31、r32、r41、r42、r43。即可得到北京这个城市对于各评价灰类的灰色评价矩阵为：

2.7 对各级指标作综合评价

对评价指标Vsi作综合评价，可记该评价结果为Bs，则：

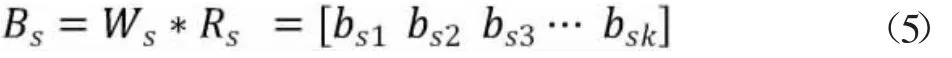
即可由公式（5）计算得出北京的评价指标Vsi的综合评价结果Bs，即：

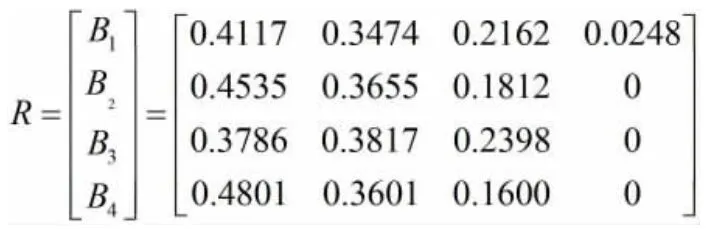
由Vsi的综合评价结果Bs，可得到各评价灰类的总灰色评价权矩阵R：

可由公式（6）得到北京的各评价灰类的总灰色评价权矩阵，即：

对于评价指标Us作综合评价，可记该评价结果为B，则：

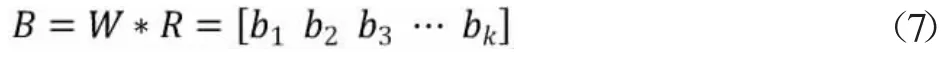
即可由公式（7）计算得出北京的评价指标Us的综合评价结果B，即：

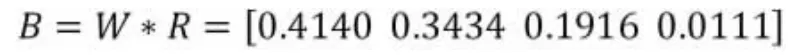
再由确定的评估灰类可得各评价灰类等级值化向量F=[9 8 6 3]，即可得城市W 的综合评价值Y，即：

由公式（8）可计算得出北京的综合评价值，即：

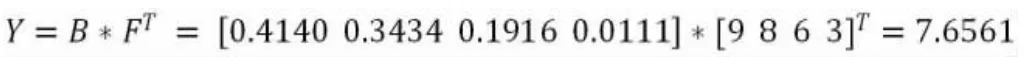
同样可按照此方法计算出所选取的余下5 个城市上海、重庆、天津、济南、合肥的综合评价值。即：Y北京=7.6561；Y上海=7.7518；Y重庆=7.4145；Y天津=6.7173；Y济南=6.3533；Y合肥=6.2886。

根据计算所得这六个城市的综合评价值，综合确定的评估灰类，可知北京、上海、重庆、天津、济南、合肥这六个城市所对应的城市共享汽车发展状况均为一般，其中Y上海>Y北京>Y重庆>Y天津>Y济南>Y合肥。即所选取的六所城市中，上海的城市共享汽车发展状况最好。

3 结束语

文章通过结合层次分析法（AHP）与灰色统计法建立了基于AHP 的灰色统计模型，并用该模型对所选取的部分城市的共享汽车发展状况做出了评估，结果显示为所选取的城市其共享汽车发展状况均为一般。结合我国共享汽车发展现状，共享汽车的发展虽然存在诸多问题，发展现状没有像国外那样好，但是可以看出共享汽车的发展有着很大的发展空间，由此足以看出该模型的评价结果具有很大的参考价值，能够客观的反映出我国城市共享汽车的发展现状。

运用此模型，同样可以推算出我国还未实行共享汽车的城市发展趋势。通过对所需实行共享汽车的城市做数据调查分析，可以对该城市共享汽车的发展趋势做出评价。若发展趋势没有达到预期标准，则可通过调节相应的影响共享汽车发展因素的指标，当影响因素的发展指标达到预期之后，共享汽车方可在该城市中投入使用，这样能够减少共享汽车投入使用所带来的亏损，从而达到最优预期标准，使各方的利益达到最大化。