水电站不同布置下的拦污浮箱流固耦合计算分析

黄振峰 ，徐朋威，李金明，肖震岳

（广西大学机械工程学院，广西 南宁 530004）

水电站进水口两岸植被差，覆盖范围广，各种垃圾杂物都随水流进入库区，所以经常堵塞上游的拦污栅，轻者水头降低，影响水电站综合效益；重则损坏拦污栅的结构，进而危及下游的发电机组。各水电站为了解决这一问题，根据自身条件增设不同结构形式的拦污排，作为进水口防护系统的第一道保障。对不同地区正在使用的拦污排研究分析后，发现两端锚固、多个浮箱相互铰接这种结构拦污性能较好，但仍有污物绕过浮箱流过，并且部分浮箱受到严重损坏。因此，有必要对不同布置的拦污浮箱进行分析研究，以便于采取更好的优化措施。

在实际水利工程中，固体和流体通常是相互作用的，为了得到更准确的研究结果，常常需要用到流固耦合分析。Sunghan 等采用大涡模拟对Re5500 ～41300 区间的圆柱近尾流场进行了研究分析，发现随着Re 数值的不断增加，在亚临界流动状态下的时均速度脉动峰值更加靠近圆柱背压点。Kwang-Jun Paik 等基于CFD 理论，分别采用单向和双向流固耦合方法对船体刚性和弹性模型进行动力学分析，最后，则通过相关实验来验证计算结果。朱凤霞等基于CFD 数值模拟理论和k−ε湍流模型，分析了拦污栅的不同截面形式对水流特性的影响，结果表明，圆形截面的拦污栅水流过渡最为平缓，水头损失最小。

综上所述，国内外学者针对物体的流固耦合特性开展了诸多研究，但是，关于水电站不同布置下拦污浮箱的研究还是处于空白区域。本文首次基于ANSYS FLUENT 多场耦合分析平台，对不同流向角下的水体-浮箱耦合模型进行求解，分析不同工况下各拦污浮箱的流固耦合特性变化规律，为水电站改善拦污效果以及浮箱的结构设计优化提供参考。

1 流固耦合数学模型

1.1 控制方程

水体-浮箱耦合问题属于流固耦合问题，在机组正常发电过程中，水体和浮箱之间有明确的耦合界面，浮箱位移比较有限。流固耦合问题遵循流体力学的三大定律，对于不可压缩的牛顿流体，其基本方程包括流体控制方程、结构控制方程和流固耦合方程。

流体控制方程。表达式为

式中：ρ为流体的密度；uj为j方向流体的速度；Uj为j方向流体的网格速度；p为压力；µ为流体的动力黏性系数；fi为i方向流体体积力。

（2）结构控制方程。结构整体的运动是由单元的运动方程式按照一定的方式叠加得到，表达式为

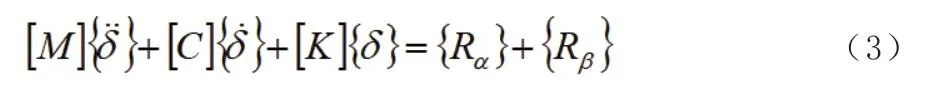
式中：[M]为结构质量矩阵；[C]为结构阻尼矩阵；[K]为结构刚度矩阵；{ }αR为流体附加动力引起的节点载荷；{ }βR为结构的其余荷载；{ }δ为结构总体节点位移列阵。

（3）流固耦合方程。在流固耦合交界位置，应该满足流体与固体应力、位移的相等或者守恒，表达式为：g表示来自流体的变量，fs 表示流体结构的相互作用，e表示来自结构的变量。

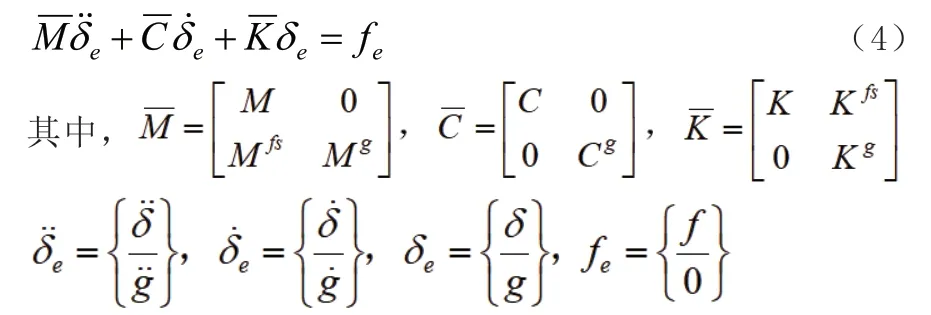
1.2 流固耦合数学模型

拦污排在进水口水域运动比较缓慢，考虑到拦污排使用性能以及自身特点，可以忽略整体结构的惯性效应。在稳定状态下，浮箱与水体流向各不相同，为了便于研究，把坐标系固定在所研究的浮箱上。如图1 所示，以浮箱底面中心为坐标原点，X 轴指向左侧销孔，Y 轴指向浮箱向水面，Z 轴垂直于水平面向上，ωV和ωθ分别表示水体随浮箱坐标系的流速和流向角。

由于水电站进水口水流特性比较复杂，为了简化分析，在浮箱定位仿真中，假设水流的方向和速度是恒定的，因此，可得作用在浮箱上的流力计算公式为：

式中，Xω是浮箱在横向所受到的流力，ωY是浮箱在纵向所受到的流力，Mω是浮箱在垂摇方向所受到的流力矩，Cxω、Cyω、Cmω分别为相应的流载荷无因次系数，L为浮箱的入水长度，εh为浮箱的入水深度，ρ为水密度。

图1 浮箱坐标系

2 数值模型建立

2.1 工程实例

以某水电站进水口胸墙式泄洪闸水体-拦污排为研究对象。在水电站正常运行过程中，拦污排的张力和形状是一定的，但各个浮箱与水体之间的流向角是不同的。由于拦污排各浮箱距离较大，忽略相互之间对流场的影响。应用三维建模软件CATIA 建立不同的水体-浮箱耦合有限元模型，并将该模型导入数值分析软件ANSYS，研究不同工况下各布置浮箱的流固耦合特性。

该水电站日均入库流量753m3/s，日均出库流量758m3/s，水头差8.16m，日均发电量1241600kWh。浮式拦污排平面布置如图2 所示，在泄流口前方水域，两端分别通过安全拉杆锚固在上支墩和下支墩，升降设备均为随水位变幅升降的全自动控制卷扬式升降设备。按照悬链线理论计算最大弧垂25m，整体设计轴线长度为237.8m，其主要结构是32 个6.7m 长的浮箱，外面完全密封，浮箱之间以若干个圆柱销和长1.2m 连杆装配而成，在坝上进水口水域形成整体的柔性结构。

2.2 有限元模型及边界条件

拦污排各浮箱在水库正常运行工作过程中，河流、空气和浮箱是一个典型的气-液-固多相流问题。由于模型体积较大，划分网格、计算收敛等仿真过程不仅对电脑的硬件有很高的要求，还需要花费很多时间和精力。为了节约时间成本，突出水载荷对各浮箱影响分析的重点，采用叠模分析将系统简化为流固耦合模型，仅考虑浮箱与水下计算域2 部分。

取水电站的进水口为计算流体，赋予其自由液面以下的相应水压力，整个流体区域长60m，宽30m，高6m，不考虑温度和能量损失，只需给出水的密度和粘度；浮箱入水深度0.59m，与圆柱销1 和销2 进行装配，所用材料均为高强度低合金结构钢，弹性模量泊松比µ=0.3。经过不断试算，根据重力相似原则对模型进行缩放，缩放比例尺为Lλ=10。采用非结构四面体网格有限元模型进行网格划分，远离流固耦合交界面区域的网格较为稀疏，在交界面区域的网格相对密集。

边界条件：FLUENT 计算域设置为高雷诺数流场，左右壁面使用对称边界条件，对于该边界的垂直方向，流动变量梯度的值为零。下表面使用无滑移壁面，上表面使用固壁边界并设置相应的滑移条件，确保该面有水流方向的速度。流场入口采用速度进口的边界条件，出口采用压力边界出口，相对压力为0Pa。湍流模型采用模型，该模型对自由液面的捕捉精度和计算可信度较为理想，相比标准k−ε模型，湍流粘度增加了旋转和曲率的内容，使流动更好地符合湍流的物理定律。

图2 水电站拦污排平面布置

3 水体-拦污浮箱耦合流场特性分析

3.1 浮箱近壁水体流速特性分析

图3 所示为90°流向角下入口2m/s 对应的三维流场和对称面流速矢量。从图3 可以看出该工况下，流场中浮箱周围流体的速度关于中心线对称，且流场分布变化比较剧烈。流体从入水口流向浮箱，在向水面驻点压力达到最大值，速度迅速减小为零，动能全部转化为压能。之后，流体绕过浮箱向下游流动时，部分压能转化为动能，最大流速出现在浮箱底部位置。当流体流经浮箱背水面时，其中一部分向下游流去，而由于浮箱周围高负压区域的存在，使得此处的另一部分流体压力急剧减小，产生回流并在背部区域形成漩涡。

图3 90°流向角下入口2m/s流速矢量（单位： m/s ）

通过实际调研发现，污物主要堆积在90°流向角浮箱附近。为进一步了解90°流向角下浮箱绕流流场的速度大小变化情况，在浮箱周边选取4 条近壁水体节线，生成节线速度位移变化曲线，浮箱近壁节线选取情况如图4 所示。

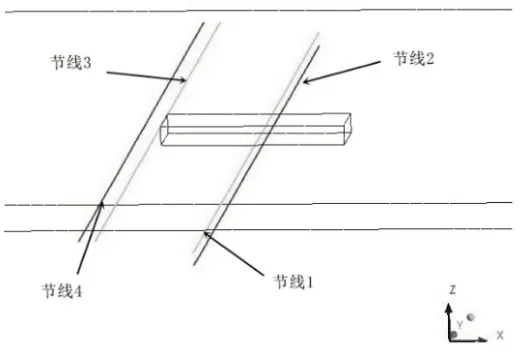
图4 浮箱近壁节线选取

图5 为不同入口流速下4 条节线速度位移变化曲线。从图中可以得出：①针对不同的入口流速，流体的速度在近浮箱区域都发生了突变，变化趋势大致相同。②在靠近浮箱流域节线1、3 速度“陡降急增”，反映了流体绕流造成的浮箱边缘涡流空化情况。而节线2、4 速度“陡增急降”，并且陡增的速度较大，甚至大于入口速度。由此说明，漂浮的污物很容易绕过浮箱底部堆积在上游拦污栅，水头减少、威胁增大、拦污排形同虚设。因此，有必要为90°流向角浮箱增设一排入水栏杆，入水深度取决于流速过渡区域的大小。③对比不同入口流速下浮箱底部的流场特性，从1 ～3m/s，节线1 最大降幅依次为86%、84%、88%，而节线2 最大增幅依次为17%、18%、21%，说明流速过渡区域与入口流速大小无关。

图6 为入口流速2m/s 近壁流体中轴线（沿Z 轴方向）速度位移分布曲线。结合模型的缩放比例尺，可以看出该类型结构拦污浮箱实际增设入水栏杆，深度h 以1.4m 最优。

3.2 浮箱近壁水体压力特性分析

图7 为入口流速2m/s 不同流向角下近壁水体压力分布云图（X0Y 平面，Z=0.05m）。由图中可以得出：压力最大点位于浮箱迎流面侧，在该位置浮箱容易受到损坏，流体到达驻点时，动能逐渐转化为压能。流向角越小，驻点位置越靠近浮箱迎流面侧的边缘，此时，会在该位置形成一定范围的负压区域；流向角越大，浮箱的迎流面积越大，近壁水体高压范围也显著变广。由于此处是浮箱水体的交界面，当流体绕过浮箱时，流体仍会在交界面边缘处发生扰动现象，在浮箱背水面的负压区域出现小范围的正压区。由于自由液面的波动和浮箱交界面的相互影响，在浮箱近背水面的尾流场中，可以看到形状不规则的涡结构。

图6 入口2m/s 近壁流体中轴线速度位移变化

图7 入口流速2m/s 不同流向角下近壁水体压力分布

将该工况下各流向角的最大、最小压力值汇集起来，如表1 所示。可以看出，30°流向角下的正压力最大，而75°流向角下的负压力和压力差最大，说明该流向角下的浮箱在长期运行的过程中极易受到损坏，在拦污浮箱的设计优化过程要重点考虑75°流向角下的水压力影响，以避免不必要的损失。

表1 不同流向角下最值压力

4 拦污浮箱结构振动分析

在FLUENT 模块入口流速2m/s 的求解基础上，文中在ANSYS-Workbench 协同仿真平台进行了水体-拦污浮箱耦合数据载荷的传递，进一步对不同浮箱结构振动固有频率进行分析。

4.1 浮箱结构分析

读取结构网格以及FLUENT 浮箱表面压力数据，加载到水体-浮箱耦合位置，60°流向角浮箱耦合位置加载压力载荷如图8 所示。结合实际情况，设置求解信息并对两端销轴施加固定约束，然后，分别对不同流向角下的浮箱进行求解，提取各自的最大变形量以及最大应力值，不同流向角下最大变形量和最大应力值曲线如图9 所示。随着流向角的增大，最大变形量和应力值也逐渐增加，然后，再逐渐减小，在75°流向角下达到最大值，再次验证了前面得出的结论。

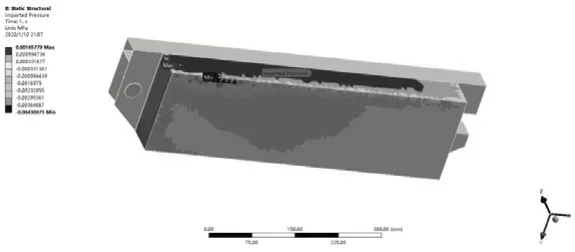
图8 90°流向角浮箱耦合位置加载压力载荷

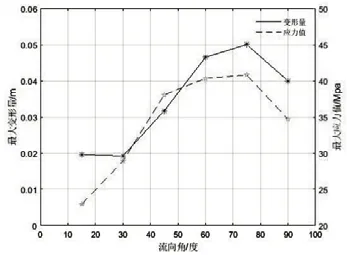
图9 不同流向角下浮箱最大变形量及应力值

4.2 浮箱预应力模态分析

将不同流向角下的压力载荷加载到浮箱的耦合位置作为预应力，施加边界条件，提取前六阶模态分析结果。60°流向角下浮箱前三阶模态振型如图10 所示，振型位移主要集中在浮箱的中部位置，该位置相对更容易遭受振动的冲击损坏。然后，与无载荷加载情况下浮箱自由振动情况的结果作对比，汇集成表如表2 所示。从表中可以对于不同流向角下的浮箱，在受到外部水载荷作用下的模态频率与自由模态相差无几，同时，可以看到，浮箱在受到外部约束的情况下，其自由振动模态频率前6 阶数值并不为0，说明刚性模态被抑制。

5 FLUENT 数值模拟验证

为验证数值模拟的准确性，首先，通过经验公式计算不同傅汝德数下的浮箱模型，得出不同流速时自由液面情况下的浮箱黏性阻力系数，然后，与应用FLUENT 计算得到的黏性阻力系数进行比较。

经验公式计算中，黏性阻力系数：

摩擦阻力系数(无量纲）采用二因次傅汝德法来进行求取：

雷诺数：

黏压阻力系数采用巴普米尔计算公式：

图10 60°流向角下浮箱前三阶模态振型

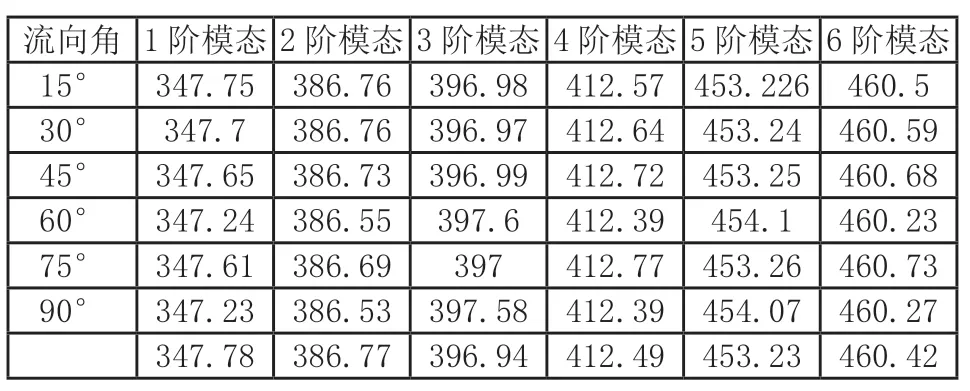
表2 不同流向角及无载荷加载下各阶模态频率/Hz

其中，Dh为水力直径，mA为浮箱中剖面面积，rL为去流段长度，Rpv为黏压阻力，S为浮箱的湿表面积。

图11为两种方法计算所得的黏性阻力系数曲线对比图。从图中可以看出，随着傅汝德数的增大，黏性阻力系数逐渐减小，而FLUENT 计算得到的黏性阻力系数略大于经验公式摩擦阻力系数和黏压阻力系数之和，这和文献[8]所得的结论相同，因此，FLUENT 数值模拟结果是合理可信的。而误差产生的原因主要是计算黏压阻力系数时只考虑了去流段的影响，没有考虑随着雷诺数的增大对黏压阻力的影响。

图11 黏性阻力系数曲线

6 结语

通过对不同流向角下的拦污浮箱流固耦合特性进行计算分析以及数值验证，得到以下结论：（1）对于实际拦污效果不好的90°流向角下拦污浮箱，底部流速过渡区域与入口速度无关，应当增设入水深度1.4m 的入水栏杆以拦截污物于第一道防线；（2）随着流向角的增大，浮箱最大变形量及最大应力值先增大后减小,而75°流向角下的压力差值最大，要重点优化该布置下的浮箱结构，以避免在水载荷的作用下造成严重损坏；（3）不同流向角下的浮箱预应力模态频率与无载荷加载时近乎一致，不同布置下的浮箱动力学特性只与自身结构特性有关。