浅析椭圆曲线数字签名的研究与发展

汪潇潇 程鸿芳

摘 要：本文介绍了椭圆曲线密码系统的发展动态和椭圆曲线数字签名方案，对其优越性进行来概括性阐述和比较性研究。最后本文对ECDSA数字签名算法的未来发展趋势进行来展望。

关键词：数字签名;椭圆曲线;信息安全

Abstract：This article describes the development of elliptic curve cryptography dynamic and elliptic curve digital signature scheme.It describes and compares its superiority to the generality of the study.Finally，this paper looks forward to the future development trend ECDSA of digital signature algorithm.

Key words：digital signature;elliptic curve;information security

1 緒论

随着信息技术的飞速发展，网络的普及，给人们生活带来了便捷，但同时也带来了隐患与危险。信息安全成为人们日益关注的热点，也成为国内外学者研究的热门话题。其中数字签名技术是其中一种安全的网络访问机制。目前数字签名广泛应用于商业领域、政府部门等。所以研究数字签名技术是非常有意义的。

2 数字签名技术

数字签名技术类似于人工签名，具有很高的安全性。数字签名的基本原理就是：发送者用其秘密解密密钥对报文进行运算，将结果传送给接收者。接收者用已知的发送者的公开加密密钥得出原报文。数字签名技术又称为公钥数字签名，基于公钥密码系统。该系统可以分成三类，如表所示：

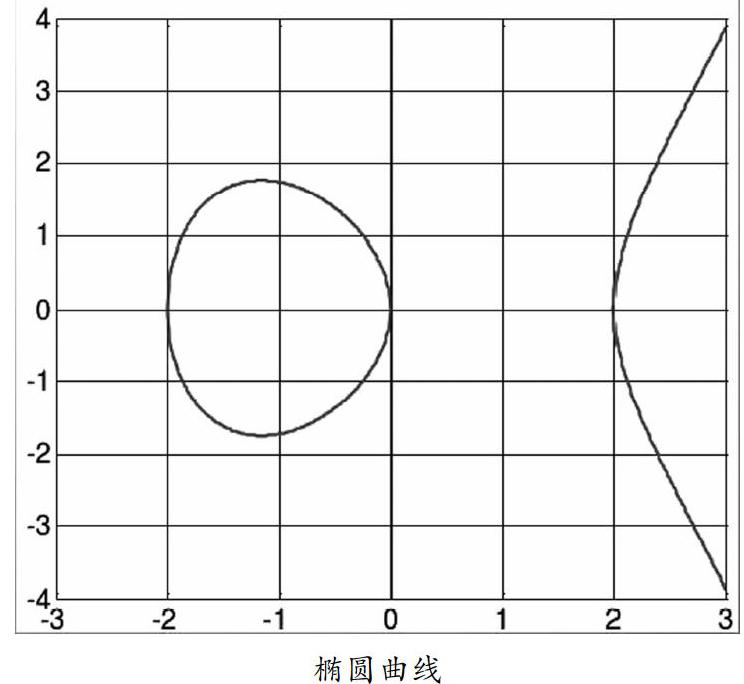
椭圆曲线的研究源于椭圆积分，如图所示：

圆曲线方程的二元三阶方程表示：y2=x3+ax+b，其中a、b为系数。

椭圆曲线密码学，简称ECC，非对称加密，是一种公开加密的算法。被公认在给定密钥长度下最安全的加密算法。应用范围很广，TLS、PGP、SSH都在使用它，特别是以BTC为代表的数字货币。

4 椭圆曲线的优势

和其他公钥体制相比椭圆曲线密码体制存在以下优势。

4.1 安全性高，加密效率高

攻击其他公钥密码体制的算法运算复杂度在椭圆曲线上离散对数问题是无效的。因此，椭圆曲线密码体制比其他的有限域上的其他公钥体制更加安全。加拿大Certicom公司在计算负荷、密钥大小和带宽三个方面做出评估：在有限计算能力的情况下，ECC相比RSA、DSA产生符合条件的密钥所花的时间最短，复杂度最少。

4.2 密钥长度小

通过攻击不同的公钥密码体制所得到的算法复杂度，在相同的安全强度下，椭圆曲线密码体制所用到秘钥长度最小，这也就说明目前每比特具有最高安全强度的密码系统是椭圆曲线密码系统[3]。也就意味着椭圆曲线密码体制对带宽和存储要求较小，开销较少。

4.3 资源丰富，灵活性好

在一个有限域中，根据椭圆曲线的定义，选取不同的参数，可以获得大量的不同的椭圆曲线，这就大大提高了系统的安全性。这由于大量的不同的椭圆曲线，可以构成一个群。由于椭圆曲线存在选择性和群结构，可以确保在一定的安全强度下，与其他密码体制相比，可以缩短秘钥长度。

5 椭圆曲线数字签名方案

（1）确定椭圆曲线的域参数：椭圆曲线的域参数有椭圆曲线E和基点G，q为域的大小，为奇数。

（2）产生椭圆曲线的密钥对：在区间[1，n-1]中选择一个随机数d，计算Q=dG，其中Q为公钥，d为私钥。

（3）生成椭圆曲线的签名：计算KG=（x1，y1），随机数k满足1

（4）椭圆曲线的签名验证：判断（r，s）是否是区间[1，n-1]内的数;计算w=s1mod n;计算u1=ew mod n和u2=rw mod n;计算X=u1G+u2 Q;计算v=x1 mod n;如果v=r时，签名成功。

6 椭圆曲线数字签名方案的硬件和软件设计

整个硬件系统主要由运算器和控制器组成。运算器包含算术运算单元和算术逻辑单元，控制器包含算术单元控制器和主控制器。运算器控制椭圆曲线的加法、乘法和求模运算，控制器控制加法、乘法和求模操作。

根据椭圆曲线签名过程，整个系统可以分成三块：密钥生成模块，签名过程模块，签名认证模块。秘钥生成模块生成系统参数，将参数存入到文件中，产生公钥和私钥;签名过程模块，利用签名算法对签名文件信息计算，计算dG，求出签名;在签名认证模块中，利用签名算法计算被签名的消息，判断签名是否有效。

7 椭圆曲线的发展动态

椭圆曲线发展至今，国内外学者都提出了不同的机制：1985年，椭圆曲线首次由eal Koblitz和Victor Miller分别独立提出的。随后Menezes提出使用特殊曲线来构建密码系统;1991年Menezes、Okamoto和、Vanstone提出利用超奇异椭圆曲线攻击椭圆曲线离散对数问题的方法，1991年，Koyama、Maurer、Okamoto和vanstone提出了基于环Zn上椭圆曲线的类RSA密码体制;1992年，Vanstone提出了基于椭圆曲线的DSA签名机制，简称ECDSA（Elliptie Curve Digital signature Algorithm）。在国内，很多学者也展开了研究。2017年张伟哲，高德智，李彦提出基于ECC的隐匿身份环签名方案;2020年肖帅，潘峰引入双参数，回避求Zp*逆运算，提出无模逆运算的椭圆曲线数字签名算法。目前椭圆曲线密码体制应用于P2P网络、无线传感网络等。

8 结语

与其他数字签名算法相比，椭圆曲线加密算法ECC有着更高的安全性。目前IEEE、ANSI、ISO、IETF、ATM等在椭圆曲线密码体制的标准化方面，开发的标准文档有IEEE P1363 P1363a、ANSI X9.62 X9.63、ISO/IEC14888等[4]。更好地发展底层运算技术，加快运算技术的效率;可以在椭圆曲线体制的基础上，结合其他密码算法，发展更高效率，更高安全性的秘钥系统;实现硬件的改进。

参考文献：

[1]D.Johnson，A.Menezes and S.Vanstone.“The Elliptic Curve Digital Signature Algorithm（ECDSA）”[J].International Journal on Information Security，2001（1）：36-63.

[2]张雁，林英，郝林.椭圆曲线公钥密码体制的研究热点综述[J].计算机工程，2004，30（3）：127-129.

[3]罗涛，易波.关于椭圆曲线数字签名算法研究[J].计算机工程与应用，2003，39（29）：184-187.

[4]罗皓，乔秦宝，刘金龙，等.椭圆曲线签名方案[J].武汉大学学报，2003，49（l）：95-98.

[5]梅挺，何大可，张仕斌.椭圆与超椭圆曲线密码体制的研究与进展[J].计算机工程与科学，2007，29（6）：10-13.

基金项目：2017年安徽省高校科学研究项目“基于移动增强现实的跟踪定位系统研究与设计”（KJ2017A560）;2017年高校优秀青年人才支持计划项目“基于移动终端的人脸识别系统的研究与设计”（gxyqZD2017141）;校级科技创新团队“AR增强现实技术科技创新团队”（Wzykj2018A02）;2020年芜湖职业技术学院横向课题“天韵”学生管理模块功能更新”（Wzyhx202004）

作者简介：汪潇潇，安徽无为人，讲师，研究方向：网络安全。

通讯作者：程鸿芳，安徽黄山人，教授，研究方向：网络安全。