梁柱简化模型在自立塔塔线体系动态响应中的适用性研究
2020-12-21杨文刚
杨文刚, 蒋 超
(华北电力大学 机械工程系,保定 071003)
1 引 言
随着非线性有限元理论的逐步成熟,有限元方法在输电线路动态响应问题的研究中得到广泛应用。文献[1]建立了三档导线有限元模型,对导线脱冰前的稳态响应、不均匀脱冰后的动态响应及稳态响应进行了整个过程的数值模拟;文献[2]通过有限元模型,提出了覆冰荷载作用下寻找输电铁塔主要失效模式的方法。文献[3,4]以实际工程为背景,建立有限元塔线体系模型,对塔线体系覆冰和脱冰工况下的力学特性进行了分析;文献[5-7]利用有限元方法,研究了导线脱冰跳跃后的振动响应;文献[8]则建立了特高压单柱拉线塔塔线体系的有限元模型,分析了单柱拉线塔脱冰动态响应的特点;对于风振响应,文献[9-11]建立了塔线体系有限元模型,施加模拟所得脉动风荷载,研究了风荷载对杆塔受力的影响;文献[12-14]运用有限元方法,研究了地震波影响下输电塔的响应分析;沈国辉等[15,16]建立了输电线路段塔线耦合体系的精细有限元模型,模拟了覆冰塔线耦合体系断线后的动态响应。
许多学者建立了桁梁混合的精细化有限元模型进行塔线体系的动力学响应研究。但导线的存在使得塔线体系模型具有大位移小应变的几何非线性特性,其动力学计算需进行非线性迭代求解,过程复杂,耗时较长,计算效率低。因此,对输电塔进行合理的力学模型简化十分必要。
王璋奇等[17,18]提出以梁柱模型简化拉线塔主柱的研究思路。其主要研究方法是通过力学计算获得输电杆塔的等效力学参数,从而用基于梁柱单元的简化模型代替桁梁混合的精细化模型。文献[19,20]使用梁柱简化法对拉线塔进行简化,建立了拉线塔梁柱简化模型,通过静动力特性分析对比验证了该方法在拉线塔体系中的合理性。自立塔与拉线塔是两类不同的结构,具有显著不同的力学特性,这种梁柱简化模型是否适用于自立塔需要进行验证。
本文提出利用梁柱简化模型计算方法建立自立塔三塔四线塔线体系模型,对自立塔进行动态响应分析。与桁梁混合精细化塔线体系模型进行静动力特性对比;并以脱冰工况为例,分析利用梁柱简化模型建立的自立塔塔线体系模型动态响应,对比验证简化模型计算精度,探讨梁柱简化模型在自立塔塔线体系动力学响应中的适用性。
2 简化模型的建立
分析自立塔时利用梁柱简化模型计算方法将自立塔简化为梁柱模型,对铁塔的每一个分段进行力学计算,如图1所示。得到梁柱简化模型的等效截面积、等效截面弯曲惯性矩、等效截面扭转惯性矩以及等效附加质量,然后利用这些等效参数建立简化模型。由此得到的简化模型,其每一个分段都能最大限度继承原有模型的整体力学特性,具有相同的拉压、弯曲和扭转刚度,达到使用简化模型代替精细化模型并简化计算的目的[20]。
2.1 拉压刚度的简化
塔身拉压刚度主要取决于主材的截面积大小,斜材的影响可以忽略。在这种情况下,主柱的截面积如图2所示。主柱等效拉压刚度计算方式为
EAe q=EA主材=E(A1+A2+A3+A4)
(1)
式中E为主材角钢材料的弹性模量,本模型取 2.1×1011Pa;Ae q为主柱的等效截面积,A1~A4为四根主材的截面积。
2.2 弯曲刚度的简化
塔段等效弯曲刚度计算方法为[20]
x向:(EIe q)x x=(EIl e gs)x x=[E(I1+I2+I3+I4)]x x
y向:(EIe q)y y=(EIl e gs)y y= [E(I1+I2+I3+I4)]y y
(2)
式中Ie q为主柱的等效截面积惯性矩,Il e gs为主材截面惯性矩之和,I1~I4分别为四根主材的截面惯性矩。

图1 模型分段方式
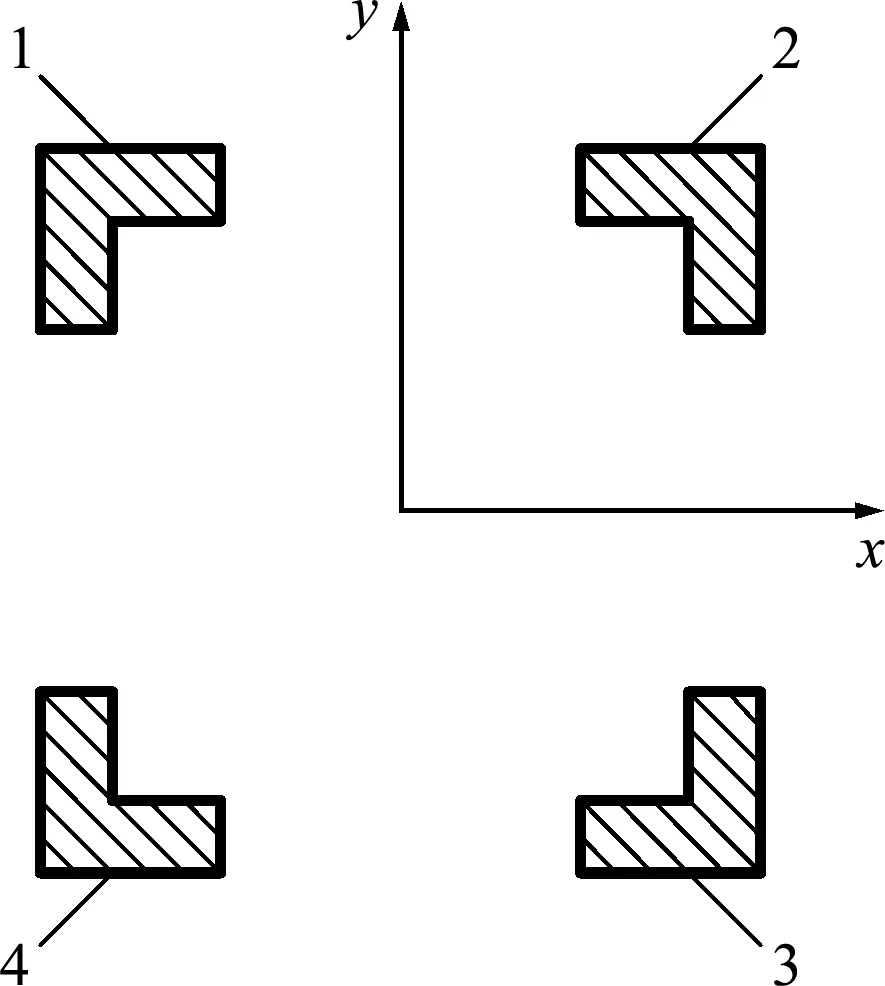
图2 主柱截面
2.3 扭转刚度的简化
在塔身或者横担发生扭转变形时,斜材的受力要比主材受力大得多,所以分析扭转刚度时主要考虑斜材的影响。
基于应变能相等的理论,提出将单片的格构式结构整体静力等效为薄板结构,由格构式结构中斜材的布置方式决定其薄板厚度的方法,即等效薄板法[21]。由此推导不同斜材和横隔材布置方式下的等效厚度的计算方法,对图3所示各种情况,推导结果如下。
布置方式(a)的等效厚度为
(3)
布置方式(b)的等效厚度为
(4)
式中E为弹性模量,G为剪切模量,a为主柱长度,b为主柱宽度,d为斜材长度,Ad为斜材截面积,Av为横隔材截面积,Al为主材截面积。
等效扭转刚度计算方法为
GJe q=Gb3te
(5)
式中Je q为等效扭转惯性矩。
2.4 附加质量的简化
利用上述方法建立简化模型,在拉压刚度、弯曲刚度和扭转刚度上具有很大的相似性,但是因为只考虑了主材的质量,忽略了斜材的质量,所以必须附加斜材的质量以保证与精细化模型质量上的相等。
(6)
式中Madd为附加质量,Mtotal为总重,lmast为总长,Aili为分段的截面积和长度。
建立的简化单塔模型如图4所示。此简化模型拥有50个节点和49个单元。
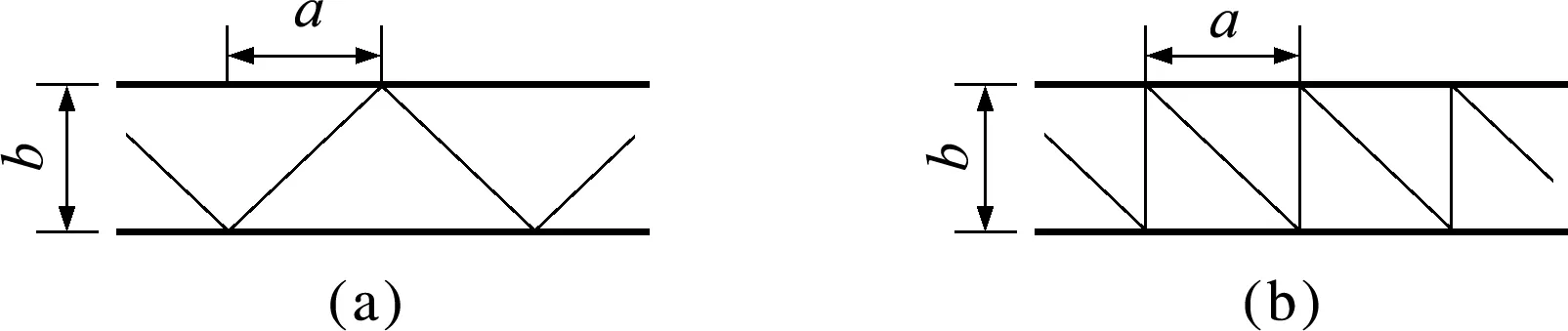
图3 几种斜材和横隔材布置方式

图4 单塔简化模型
3 精细化模型与塔型体系模型的建立
建立自立塔的精细化模型,主材单元和横隔材处理为梁单元,斜材和辅助材处理为杆单元,如 图5 所示。此精细化模型拥有180个节点和604个单元。
建立的塔线体系简化有限元模型如图6所示,作为研究对象的中间塔为精细化有限元模型,两侧塔为简化有限元模型。而建立的塔线体系精细化模型作为对比模型,三塔均为精细化有限元模型,如图7所示。
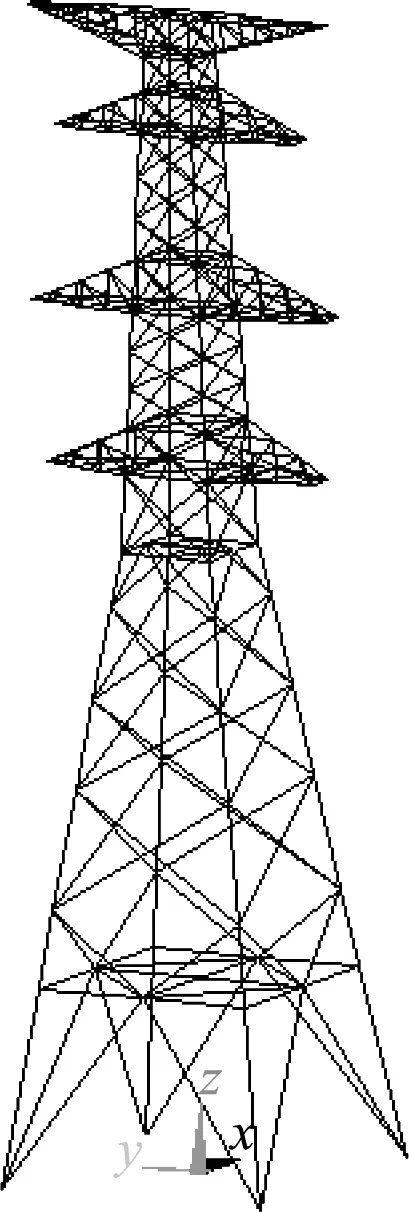
图5 单塔精细化模型

图6 塔线体系简化模型

图7 塔线体系精细化模型
4 单塔精细化模型和简化模型静动力特性比较
对单塔精细化模型和简化模型进行90°风荷载下的静动力特性分析,对比其结果。
4.1 静力特性比较
该自立塔水平档距为350 m,设计风速为 33 m/s,地形地貌属于B类地区。在简化模型和精细化模型初始状态相同的条件下,施加相同的风荷载,得到自立塔变形情况如 图8 所示。提取两模型塔身顺风向位移并绘制两模型主柱节点位移随高度的变化情况,如图9所示。可以看出,在90°大风荷载下,简化模型塔身的位移与精细化模型基本重合,因此,在静力特性上,自立塔的简化模型与精细化模型基本一致。
4.2 动力特性比较
研究结构的动力特性是进行结构动力响应分析的基础。对精细化模型和简化模型的模态进行对比分析。提取前三阶的固有频率和振型,结果列入表1,振型如图10~图12所示。对比频率和振型发现,精细化模型和简化模型前三阶的振型相同,振动的频率值也比较接近,两者低阶的动力特性基本一致。
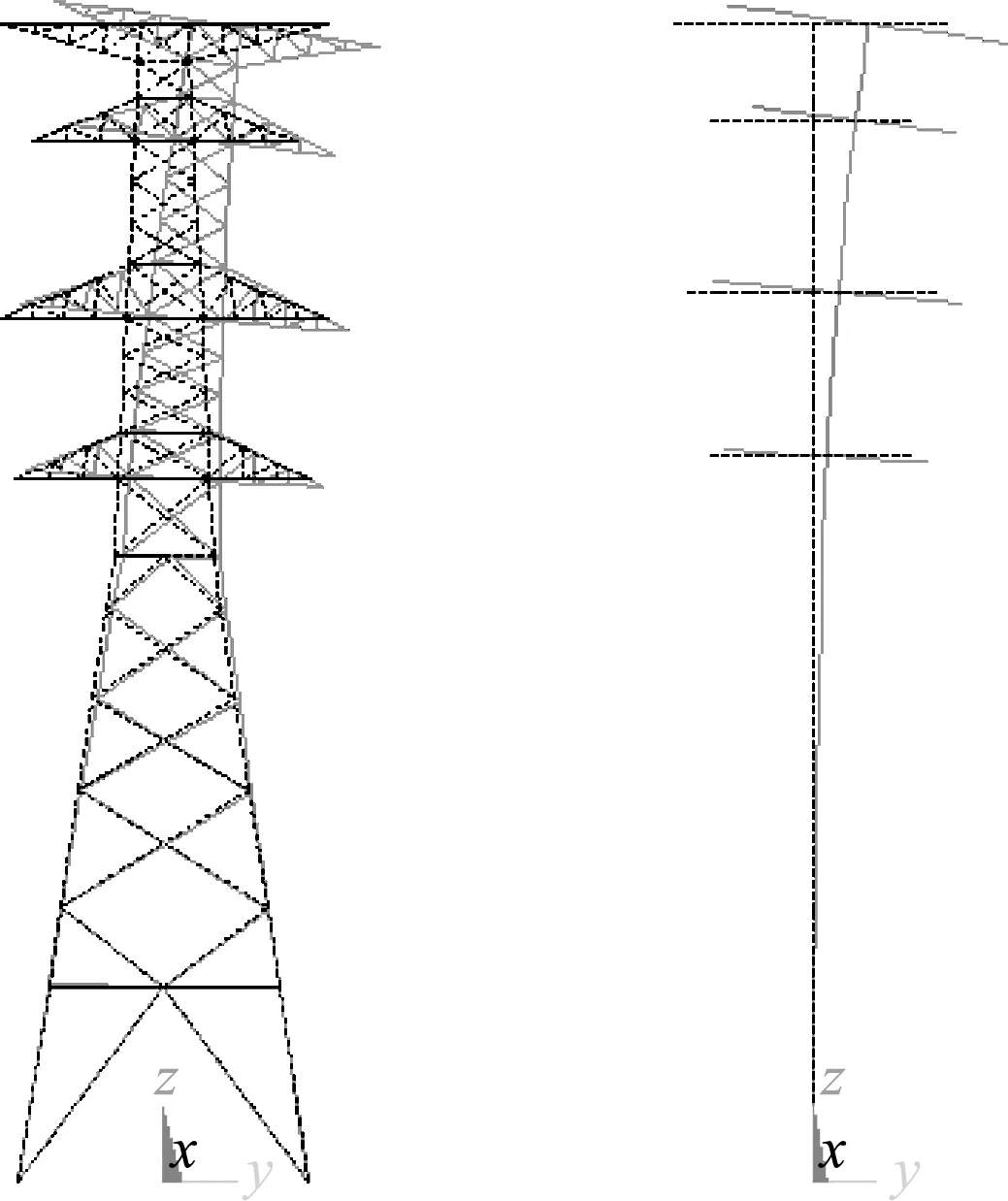
图8 垂直导线方向弯曲变形情况

图9 垂直导线方向弯曲节点位移变化
5 塔线体系的动力特性
对比塔线体系简化模型和精细化模型的模态分析结果证明塔线体系简化模型的合理性。
对自立塔塔线体系精细化模型和简化模型进行模态分析对比。其典型阶数频率列入表2,发现两种模型的频率非常接近。为了更直观地对两种模型的振型进行对比,提取两种模型的整体第1和第29阶振型如图13所示,发现两种模型的整体振型是一致的。综上所述,自立塔塔线体系简化模型和全精细化模型动力特性一致,可利用塔线体系简化模型代替全精细化模型进行计算。

图10 一阶振型

图11 二阶振型
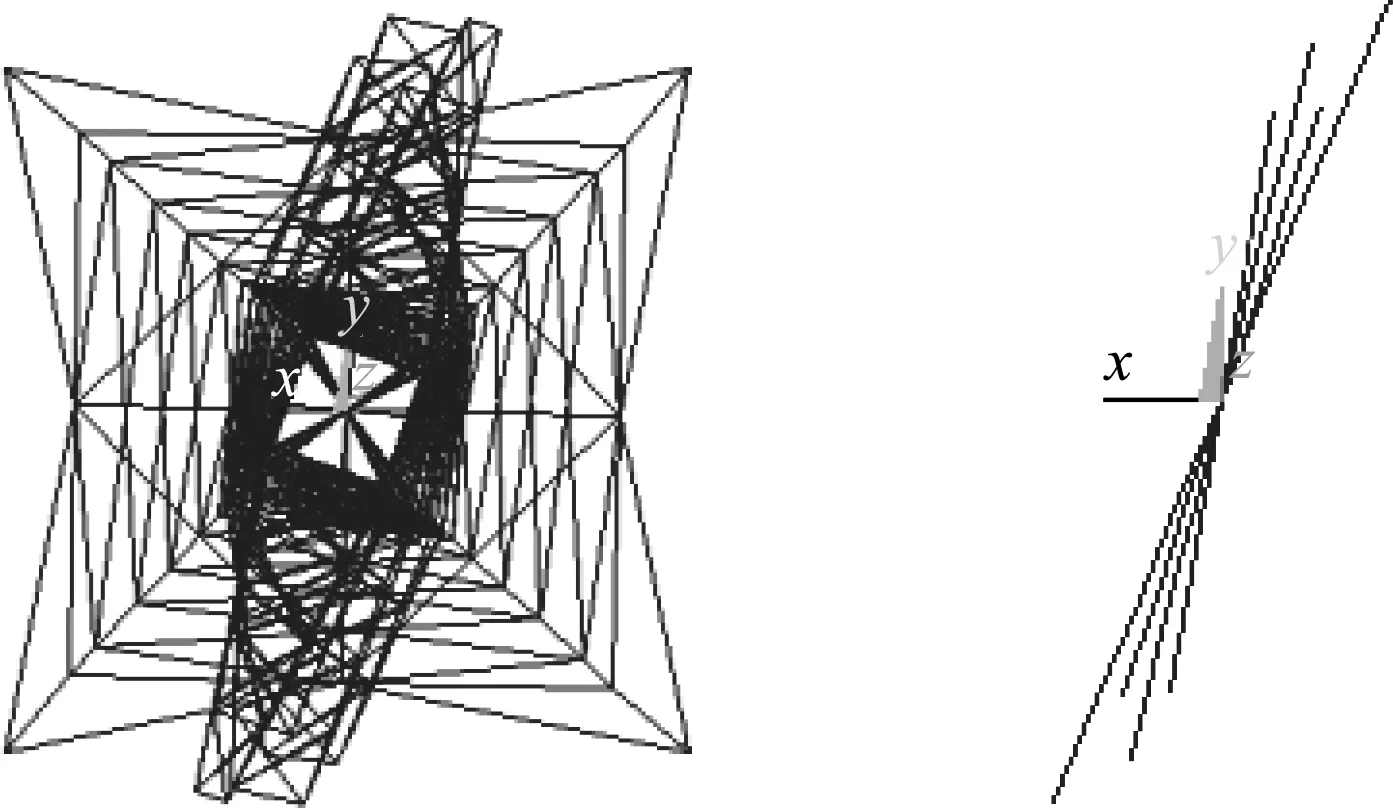
图12 三阶振型
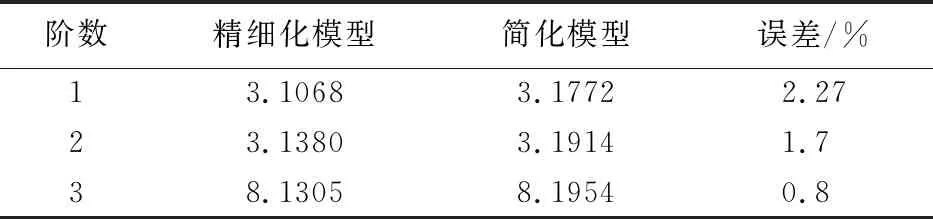
表1 模态频率及误差
6 塔线体系脱冰动态响应对比研究
文献[22,23]为研究集中质量法模拟覆冰在架空线脱冰动张力实验的适用性,建立档距为11.3 m的孤立档架空线实验模型,从而验证了集中质量法模拟覆冰的准确性。
因此本文将施加在输电线节点上的集中质量单元杀死来模拟覆冰脱落,使用ANSYS瞬态动力分析方法来计算输电线脱冰后塔线体系的动态响应。
6.1 脱冰工况分析
为便于下文分析,对导线和杆塔进行编号。如图14所示,导线自左到右分为A,B,C和D四档,自上向下依次编号1~4,杆塔自左向右依次编号1#~3#,规定坐标系中x方向为顺线路方向,y方向为垂直线路方向,z方向为竖直方向。
选取两种产生强扭转荷载的导线脱冰工况,脱冰工况具体设置如下。
工况1:C档2号和4号导线脱冰,即单档导线脱冰。
工况2:B档1号和3号导线脱冰,C档2号和4号导线脱冰,即反向的两档导线脱冰。
导地线覆冰厚度取设计覆冰厚度为10 mm,脱冰量为100%,脱冰过程中不考虑温度和风力等因素的影响。
6.2 塔头位移对比分析
在脱冰工况中,塔头会产生水平面内的刚体转动,绘制塔头两端节点156和170(图15)竖直方向位移时程曲线进行对比分析,如图16和图17所示。
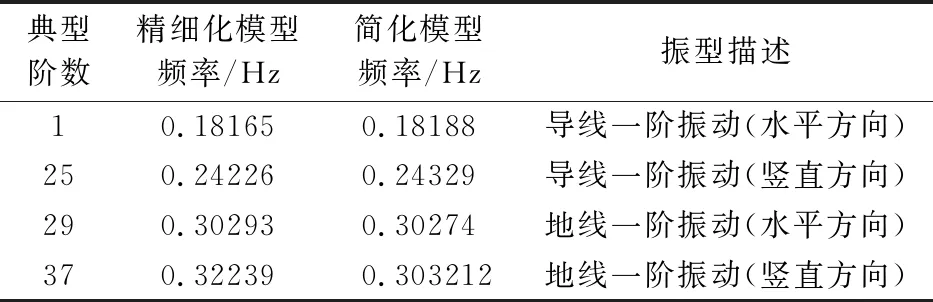
表2 两种塔线体系模态对比

图13 塔线体系模型振型
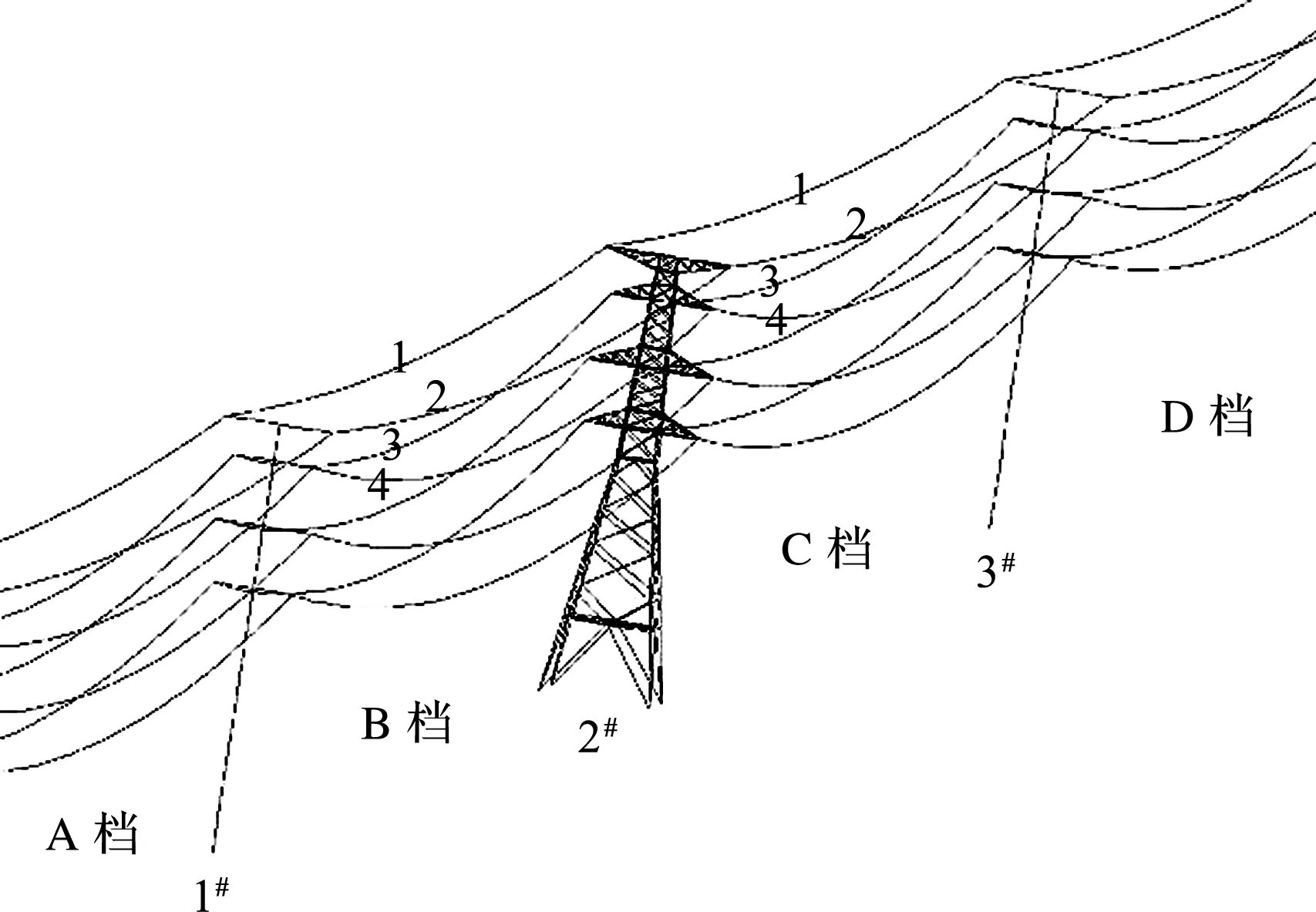
图14 导线和杆塔编号
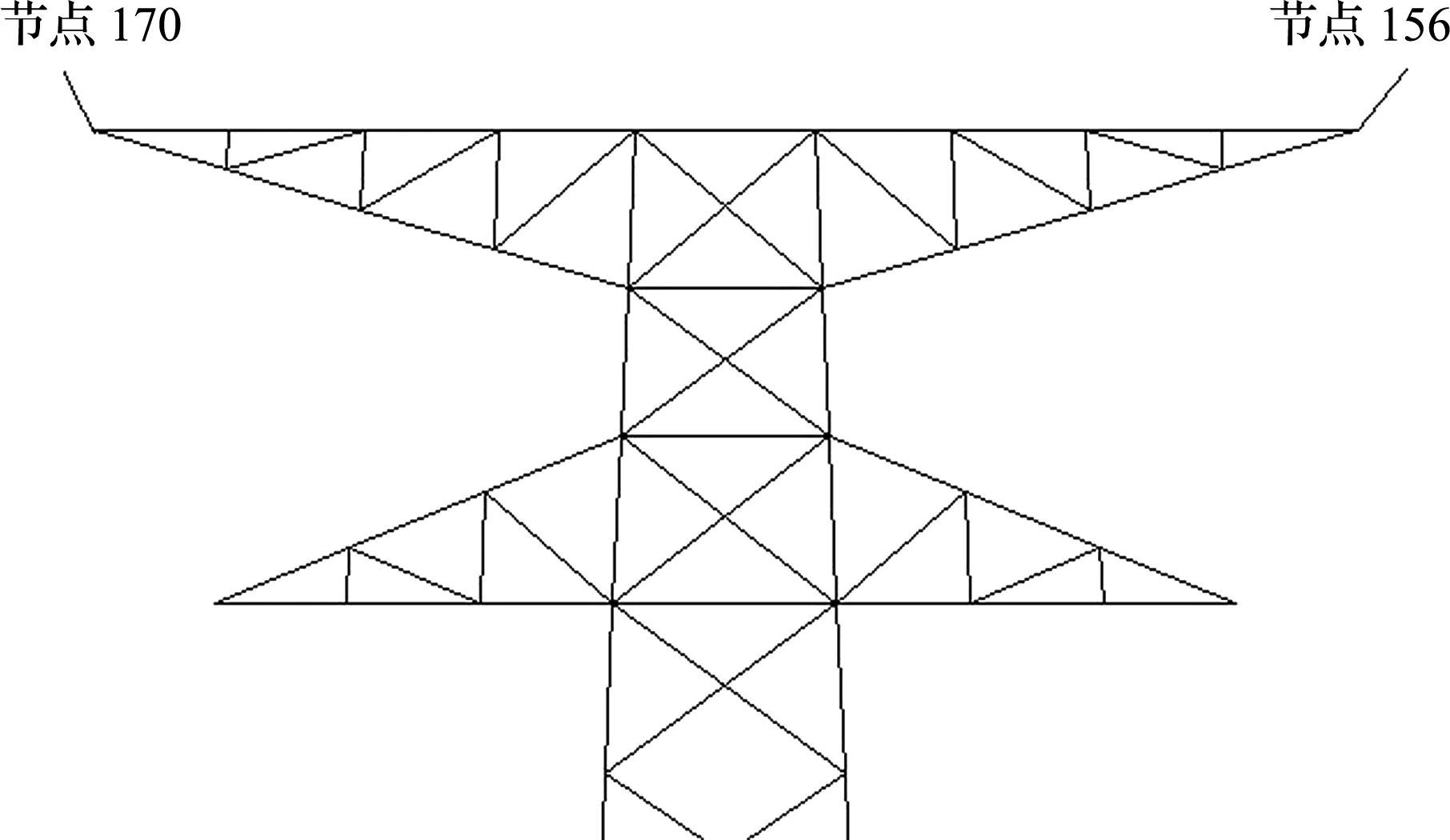
图15 塔头单元节点位置
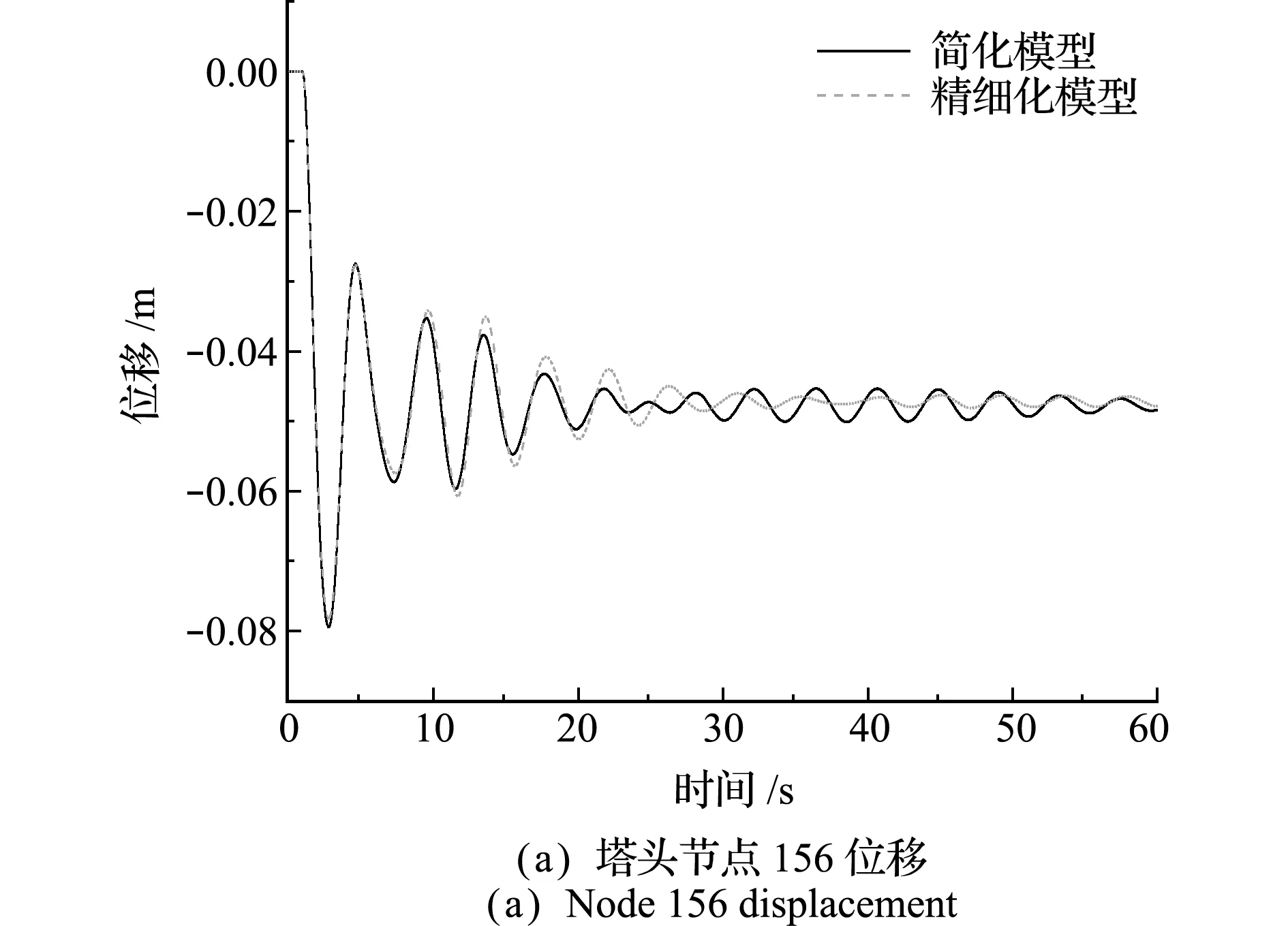
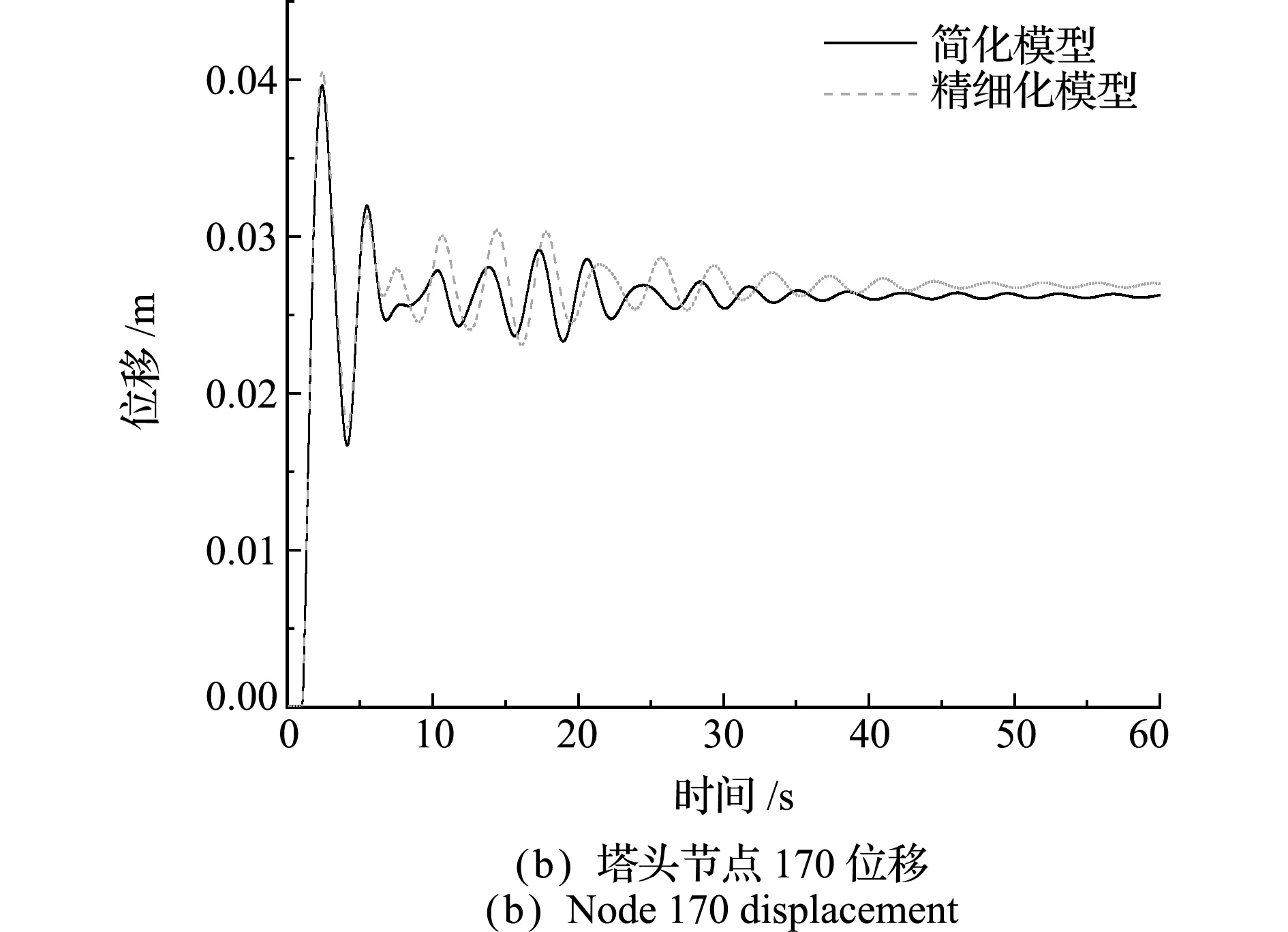
图16 工况1顺线路方向位移对比
在单档导线脱冰工况中,从图16可以看出,塔头两端的节点在顺线路方向的位移方向相反,脱冰侧位移最大值简化模型为0.0795 m,精细化模型为0.0783 m,误差为1.5%。未脱冰侧位移最大值简化模型为0.0396 m,精细化模型为0.0404 m,误差为2%。在反向两档导线脱冰工况中,如图17所示,由于铁塔两侧的脱冰条件相同,所以塔头两端节点位移量基本一致,对比简化模型和精细化模型顺线路方向位移,发现各节点位移大小吻合,误差仅为1%。
6.3 扭转位移分析
绘制塔身44.5 m(顶端)和34.2 m(中部)高度截面转角时程曲线,对比简化模型和精细化模型扭转位移误差,验证简化模型的适用性。
在脱冰工况中,从图18和图19可以看出,塔身截面转角在导线覆冰脱落一段时间后达到峰值,然后逐渐衰减震荡。简化模型和精细化模型均满足这一运动趋势。

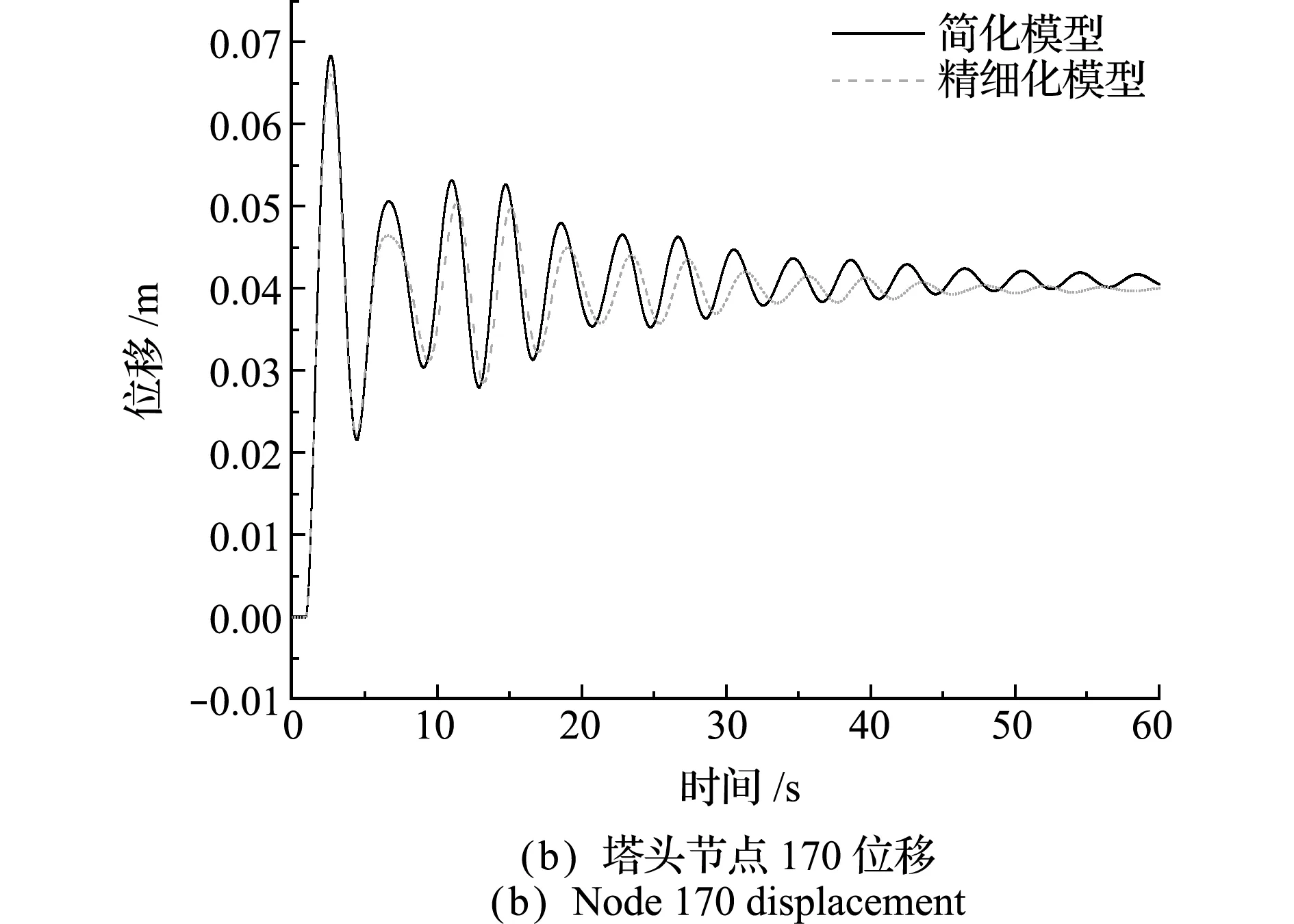
图17 工况2顺线路方向位移对比


图18 工况1扭转位移对比


图19 工况2扭转位移对比
在单档脱冰过程中,如图18所示。塔身顶端扭转位移最大值简化模型为0.3069°,精细化模型为0.3016°,误差为1.7%;塔身中部扭转位移最大值简化模型为0.1269°,精细化模型为0.1248°,误差为1.6%。在反向两档导线脱冰工况中,如图19所示,塔身顶端扭转位移最大值简化模型为 0.6192°,精细化模型为0.5987°,误差为2%;塔身中部扭转位移最大值简化模型为0.2691°,精细化模型为0.2641°,误差为1.9%。
6.4 塔身主材轴力分析
在单档脱冰过程中,提取塔身44.5 m(顶端)和34.2 m(中部)主材单元轴力,如图20所示。分析脱冰过程中两种模型塔身主材受力情况,对比时程曲线的振动趋势。
对比轴力时程曲线,发现塔身顶端最大轴力简化模型为48.39 kN,精细化模型为47.58 kN,误差为1.6%;塔身中部轴力最大值简化模型为 98.64 kN,精细化模型为96.78 kN,误差为1.8%;此外,整体过程中误差均在3%以内。
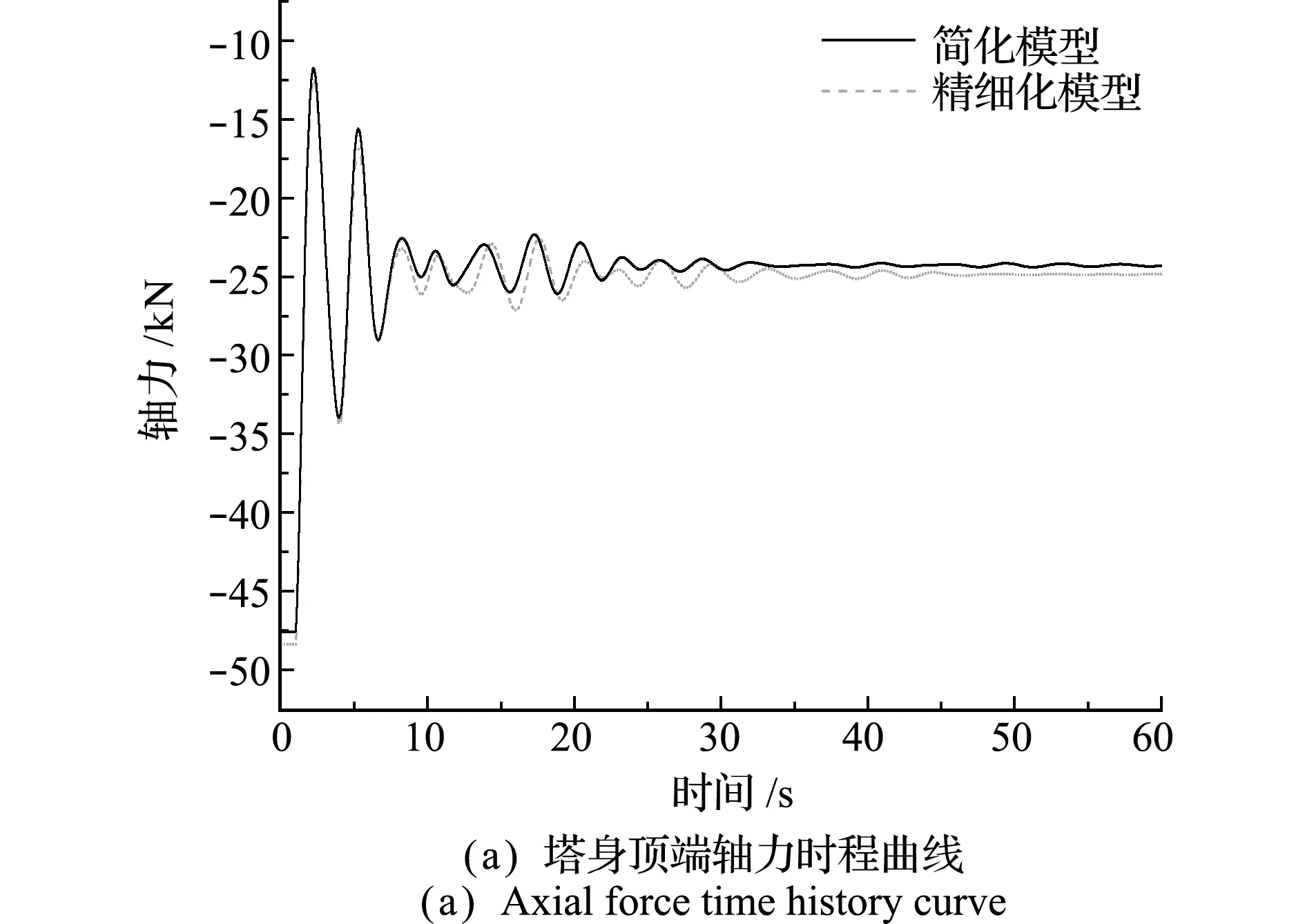
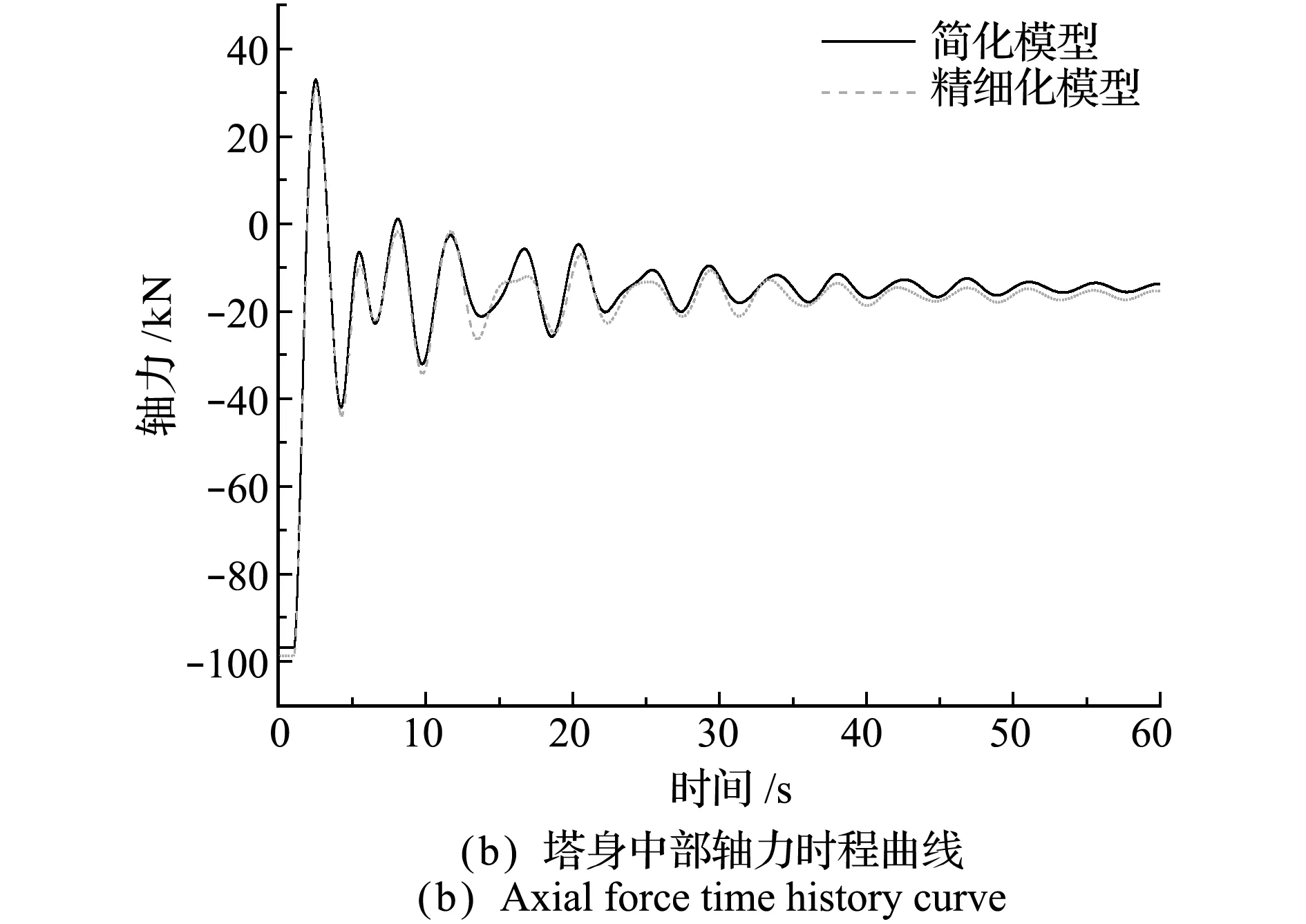
图20 塔身轴力对比
7 结 论
本文提出利用梁柱简化模型计算方法对自立塔进行简化。建立自立塔单塔的梁柱简化模型和塔线体系模型,与桁梁混合精细化模型进行静动力特性分析对比;并以脱冰工况为例,探讨梁柱简化模型在塔线体系在动态响应中的适用性。结果表明:
(1) 采用梁柱简化模型计算方法对自立塔进行仿真计算,与桁梁混合模型对比,单塔拉压变形和弯曲变形误差小,低阶的振型相同,振动的频率值误差小,低阶动力特性基本一致,可有效保证计算精度,完成工程计算。
(2) 基于精细化模型的塔线体系和基于梁柱简化模型的塔线体系的位移时程和内力时程的最大值接近,两者的时程曲线的振动趋势吻合。因此,在进行自立塔塔线体系的动态响应分析时,可选择梁柱简化模型参与计算,以提高计算和分析效率。
