CFB锅炉可调效率的旋风分离器性能数值模拟研究

袁东辉，孙世超，郑秀平，韩 义，王研凯，段伦博

(1.内蒙古电力(集团)有限责任公司 内蒙古电力科学研究院分公司，内蒙古 呼和浩特 010020；2.东南大学 能源热转换及其过程测控教育部重点实验室，江苏 南京 210096；3.内蒙古京泰发电有限责任公司，内蒙古 鄂尔多斯 017000)

0 引 言

近年来，我国新能源发电量和发电量占比稳步提升，其间歇性和波动性的特点对电网稳定运行影响巨大，要求新能源发电大规模并入电网后需要进行密切协调配合，降低新能源发电不稳定带来的安全调度风险，保证电网稳定运行。为了保证电网的稳定、调度以及最大程度的消纳新能源发电，传统燃煤机组如循环流化床机组等需要参与到深度调峰中。与此同时，深度调峰给循环流化床锅炉带来了低负荷时床温过低的问题。

为了解决这一问题，文献[1]提出了通过降低旋风分离器分离效率减少循环灰量从而提高炉膛温度的方法，有望改善现有锅炉运行中通过密封返料阀放灰的问题，同时，也报道了一种分离效率可调的循环流化床锅炉旋风分离器，其基本工作原理是在旋风分离器锥形筒处通入干扰风，人为控制旋风分离器内的流场，从而调控旋风分离器的分离效率。该文对这种分离效率可调的旋风分离器进行了冷态试验和数值模拟研究，证实了干扰风的通入确实可改变分离效率，但并未研究干扰风通入对旋风分离器的内部流场和压降的影响规律及其对锅炉低负荷床温的影响规律。

旋风分离器压降关系到系统的能量消耗以及风机的合理设计，在旋风分离器的设计及改造中对旋风分离器的压降进行预测具有重要意义。前人提出了一系列旋风分离器压降计算模型，如Shepherd & Lapple模型[2]、Cascal& Martinez模型[3]、Dirgo模型[4]、First模型[5]、Chen-Shi模型[6]等。上述模型均是基于试验结果、理论分析提出的，在建立的过程中进行了一定程度的简化，且模型的使用有前提条件。

近年来，采用计算流体力学(CFD)研究旋风分离器的压降发展迅速。杜慧娟等[7]利用数值模拟对280 t/h CFB锅炉中入口收缩角度分别为14°、20°、25°、30°、34°的旋风分离器进行研究，结果表明，分离效率随着收缩角度的增大先增加后减小，收缩角越大，分离器压降越高。黄中等[8]模拟结果表明，随着中心筒直径减小，循环流化床锅炉旋风分离器进出口压降差减小了16%。由洋等[9]采用Fluent研究循环流化床锅炉旋风分离器的不同结构对压降的影响，结果表明，除了入口截面积和中心筒直径对压降有影响外，中心筒的插入深度、中心筒底端与折流板之间的距离、折流板几何尺寸以及入口流速等均会对压降产生影响。张建等[10]也通过Fluent软件并借助其中的RSM模型研究旋风分离器的压降，通过与压降经验公式对比，得出CFD数值模拟能够较好地预测旋风分离器的压降。李敏等[11]以旋风分离器切向速度模型为研究对象，通过CFD模拟方法研究了分离器的压降，CFD模拟结果与压降理论计算模型的计算结果基本吻合。Ashry等[12]采用数值模拟研究非球形颗粒对旋风分离器压降的影响并与试验结果进行对比，结果表明，CFD模拟能够有效反映旋风分离器内非球形颗粒流的压降特性和分离效率。

本文以某300 MWe循环流化床锅炉旋风分离器为研究对象。首先采用CFD模拟研究不通干扰风时不同入口风速下的压降变化规律，并将压降变化规律与前人提出的分离器压降计算模型的计算结果进行对比；然后研究通入干扰风后分离效率可调旋风分离器的内部流场和压降的变化规律；最后结合热力计算，考察了通入干扰风对锅炉低负荷运行床温的影响规律，为循环流化床锅炉旋风分离器改造提供数据支撑。

1 研究内容

1.1 研究对象

本文的研究对象为国内某300 MWe循环流化床锅炉的旋风分离器。首先利用SolidWorks软件对旋风分离器进行几何构建，规定竖直方向向上为y轴正方向，中心筒出口圆心处为坐标系原点，并利用ICEM软件进行网格划分。经网格无关性验证，并结合计算精度和计算成本，最终确定网格数为114.7万。旋风分离器具体结构及网格划分如图1所示。

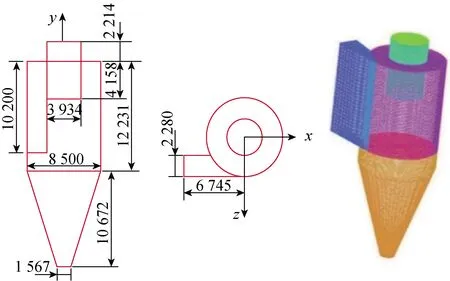
图1 循环流化床锅炉旋风分离器结构及网格划分

图1中，旋风分离器的锥形筒开孔，4个孔的直径均为120 mm，开孔圆心所在平面距中心筒出口平面14 900 mm。将旋风分离器入口方向的开孔命名为0°孔，从入口方向俯视顺时针依次旋转90°，分别命名为90°孔、180°孔、270°孔，如图2所示。

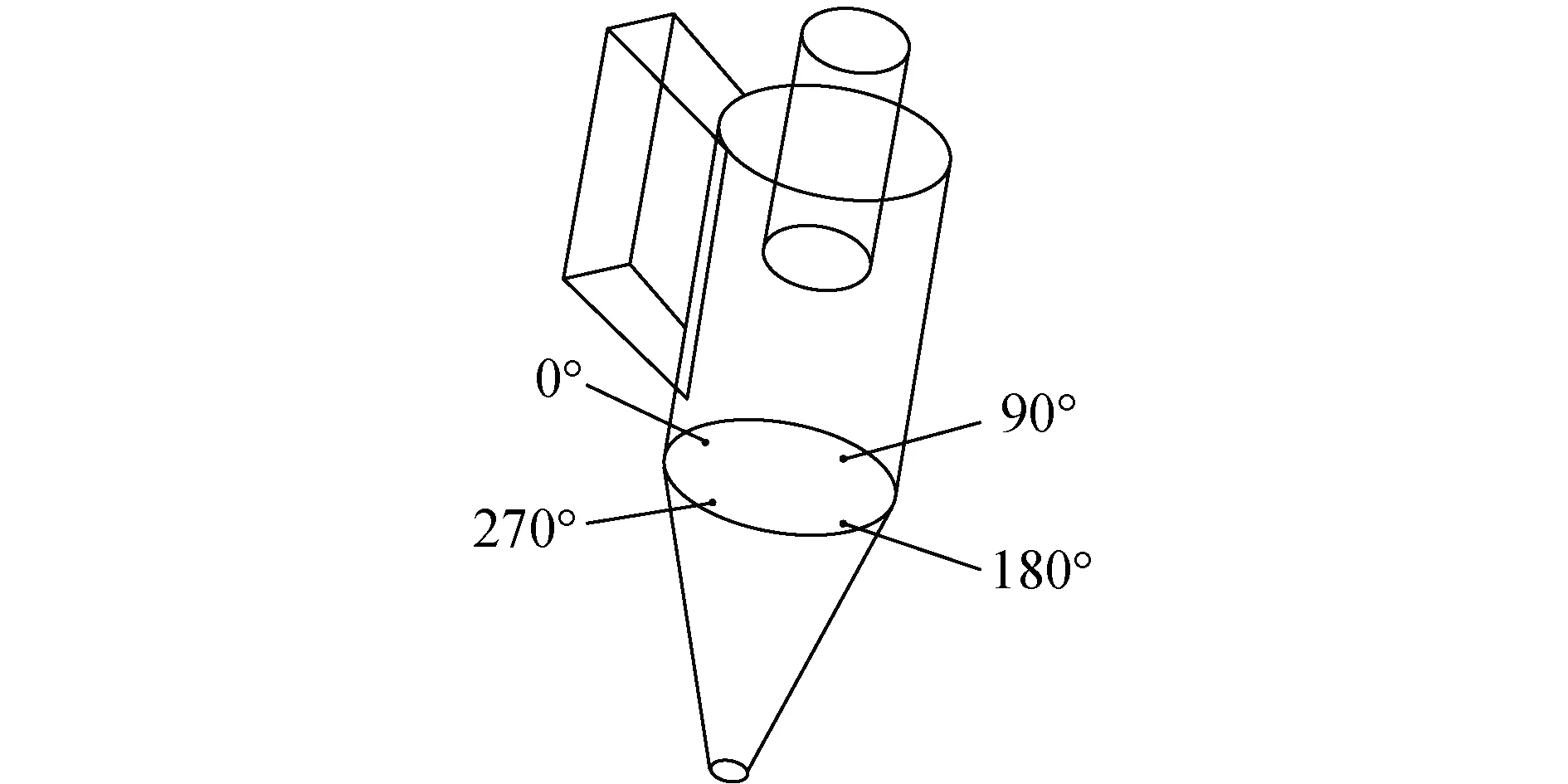
图2 循环流化床旋风分离器开孔

文献[1]通过冷态试验和数值模拟报道了向上述孔通入干扰风对旋风分离器分离效率的影响规律，本文在此基础上分析压降的变化情况并结合热力学计算，研究通入干扰风对锅炉低负荷运行床温的影响规律。

1.2 旋风分离器数值模拟

旋风分离器工作时内部的流场是复杂的三维强旋流，研究表明[12-16]，雷诺应力模型(RSM)能够较好地反映流场内部的各向异性，因此可用来模拟旋风分离器内部的三维强旋流，因此本文湍流模型选用雷诺应力模型。

压力速度耦合选择SIMPLE算法，空间离散化采用Green-Gauss Cell Based算法。边界条件中入口采用速度入口(velocity-inlet)，中心筒出口采用完全流出口(outflow)，壁面采用无滑移边界。分离器入口气体温度为737 ℃，入口颗粒密度为1 200 kg/m3，质量浓度为0.36 kg/m3，入口颗粒假设为球形，粒径分布如图3所示，气固曳力模型采用spherical模型。干扰风温度为27 ℃，干扰风速分别为10、20、30 m/s。多粒度入口条件下旋风分离器分离效率的计算方法如下：利用颗粒的粒径分布划分若干质量组，每组的质量分数与该组平均粒径下的分级分离效率相乘，全部组的总和即为总分离效率[17]，计算公式为

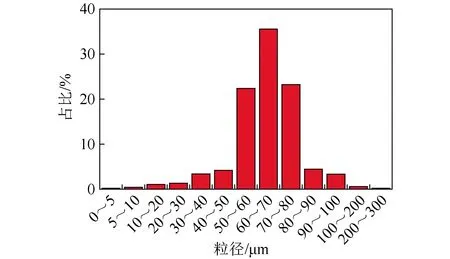
图3 入口颗粒粒径分布

η=∑ηxMx，

(1)

式中，η为总分离效率，%；ηx为平均粒径为dx颗粒的分级分离效率，%；Mx为平均粒径为dx颗粒质量组的质量分数，%。

本文利用CFD模拟研究循环流化床锅炉分离效率可调旋风分离器不通入干扰风且入口速度变化时的压降变化，并与Shepherd & Lapple计算模型、Cascal & Martinez计算模型、Dirgo计算模型、First计算模型、Chen-Shi计算模型等计算结果进行对比。此外利用CFD模拟研究循环流化床锅炉分离效率可调旋风分离器在115 MWe负荷时(入口速度为7.48 m/s)通入干扰风的压降变化规律。分离效率可调旋风分离器模拟工况见表1。

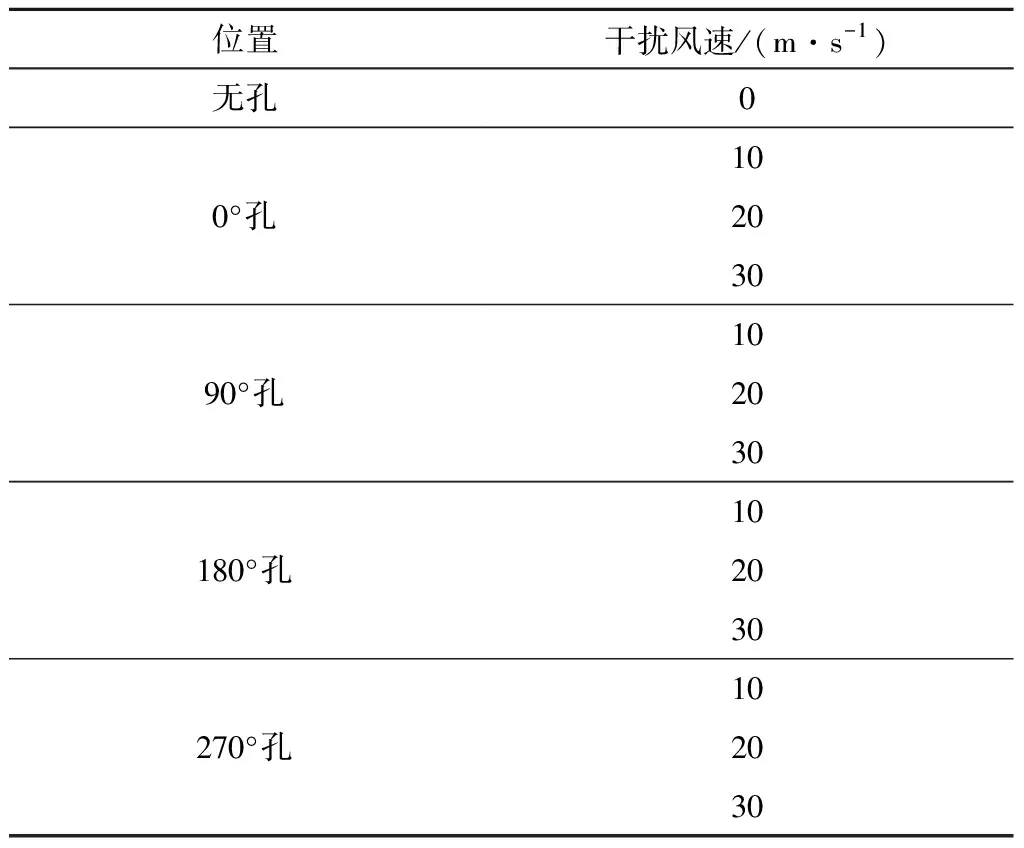
表1 分离效率可调旋风分离器模拟工况

1.3 压降计算模型

旋风分离器压降与旋风分离器入口流速的平方成正比，因此通常将旋风分离器的压降表示为

(2)

式中，ζ为阻力系数；vi为旋风分离器入口流速，m/s；ρ为进口气体密度，kg/m3。

式(2)为计算旋风分离器压降的通用计算公式，其中ζ可以看成除了分离器进出口气流动压外的其他影响因素的综合影响[19]。不同计算模型的阻力系数的计算方法不同，本文采用5个计算公式，即

Shepherd & Lappe模型：

(3)

Cascal & Martinez模型：

(4)

Dirgo模型：

(5)

First模型：

(6)

Chen-Shi模型：

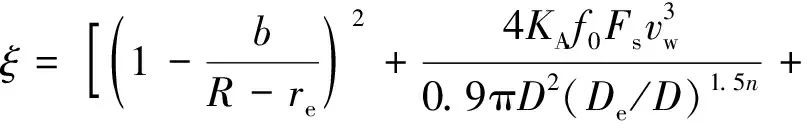
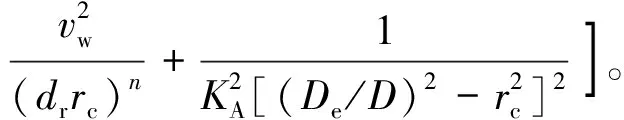
(7)

式中，a、b分别为分离器入口高度和宽度，m；B为锥形筒底端直径，m；De、re分别为中心筒直径和半径，m；D、R分别为筒体直径和半径，m；H、h分别为分离器和筒体高度，m；S为中心筒插入深度，m；KA为入口面积比，KA=πD2/(4ab)；rc为核心流半径，m；Fs为总接触面积，m2；vw为筒体半径处的切向速度，m/s；dr为中心筒直径与筒体直径之比；f0为气流与旋风分离器内壁之间的摩擦因数。

筒半径处的切向速度采用式(8)[6]进行计算，即

(8)

2 结果与分析

旋风分离器的压降定义为旋风分离器进出口的静压差，即

ΔP=Pin-Pout，

(9)

式中，Pin为旋风分离器入口静压，Pa；Pout为旋风分离器出口静压，Pa。

2.1 不同入口速度下的压降

由于本文研究的旋风分离器处于115 MWe低负荷运行，旋风分离器入口速度较低，因此取入口速度分别为6、8、10、12、14 m/s。图4为不通干扰风的旋风分离器在入口速度为6～14 m/s时压降的模型计算结果和模拟结果。可以看出，旋风分离器的压降随入口速度的增大而增大，这与张建等[10]、李敏等[11]研究结果相同，且采用雷诺应力模型模拟的结果与计算模型中的Chen-Shi模型计算结果吻合较好。

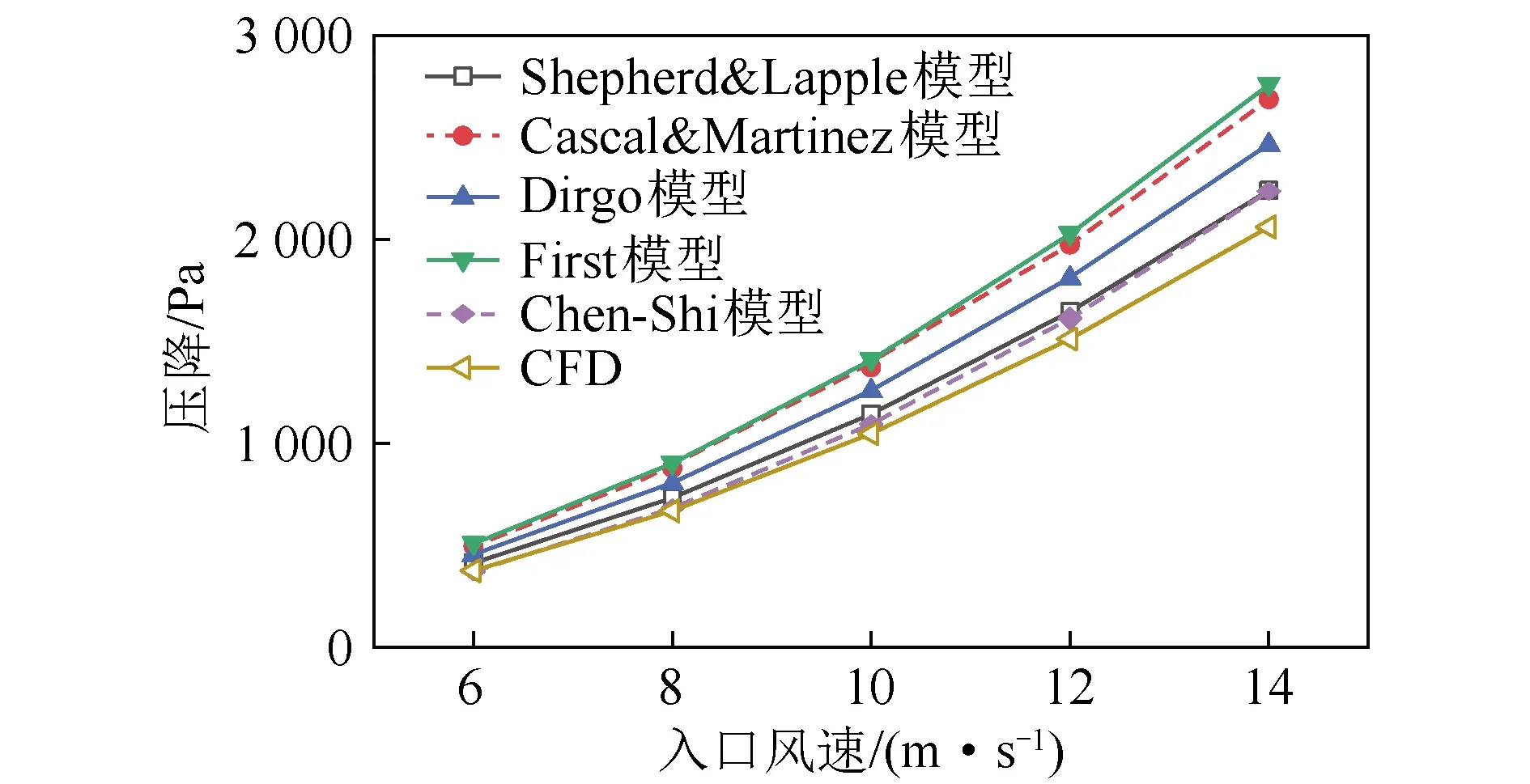
图4 不同入口速度压降模拟值与压降模型计算值

许多研究人员将CFD压降模拟结果与不同压降计算模型的计算结果进行对比，得到不同的结果。李敏等[11]利用CFD模拟得到的压降计算结果与Dirgo模型的计算结果最接近。蔡安江[22]经分析认为Shepherd-Lapple的计算公式简单，但比First的计算结果要好。钱付平等[21]发现，CFD模拟结果与Dirgo模型以及Cascal& Martinez模型计算结果较接近。张建等[10]发现，Cascal& Martinez模型较精确。杜慧娟等[7]认为CFD计算结果与Chen-Shi模型计算结果相符。

本文认为Chen-Shi模型考虑了旋风分离器的入口膨胀损失、中心筒入口处的收缩损失、旋流损失、出口处气体动能的耗散损失，在计算压降时考虑较全面，因此该模型较精确，CFD计算结果真实可信。

2.2 气相流场分析

2.2.1静压分布

在分析旋风分离器内部流场时需分析静压分布规律，而分析静压分布规律主要考虑其沿径向上的分布。本文以旋风分离器出气口水平面为0 m面，沿y轴负方向向下划分-6.5、-10.0、-11.0、-12.5、-13.5、-14.4 m等水平面，用于分析旋风分离器内部的静压径向分布，平面分布如图5所示。

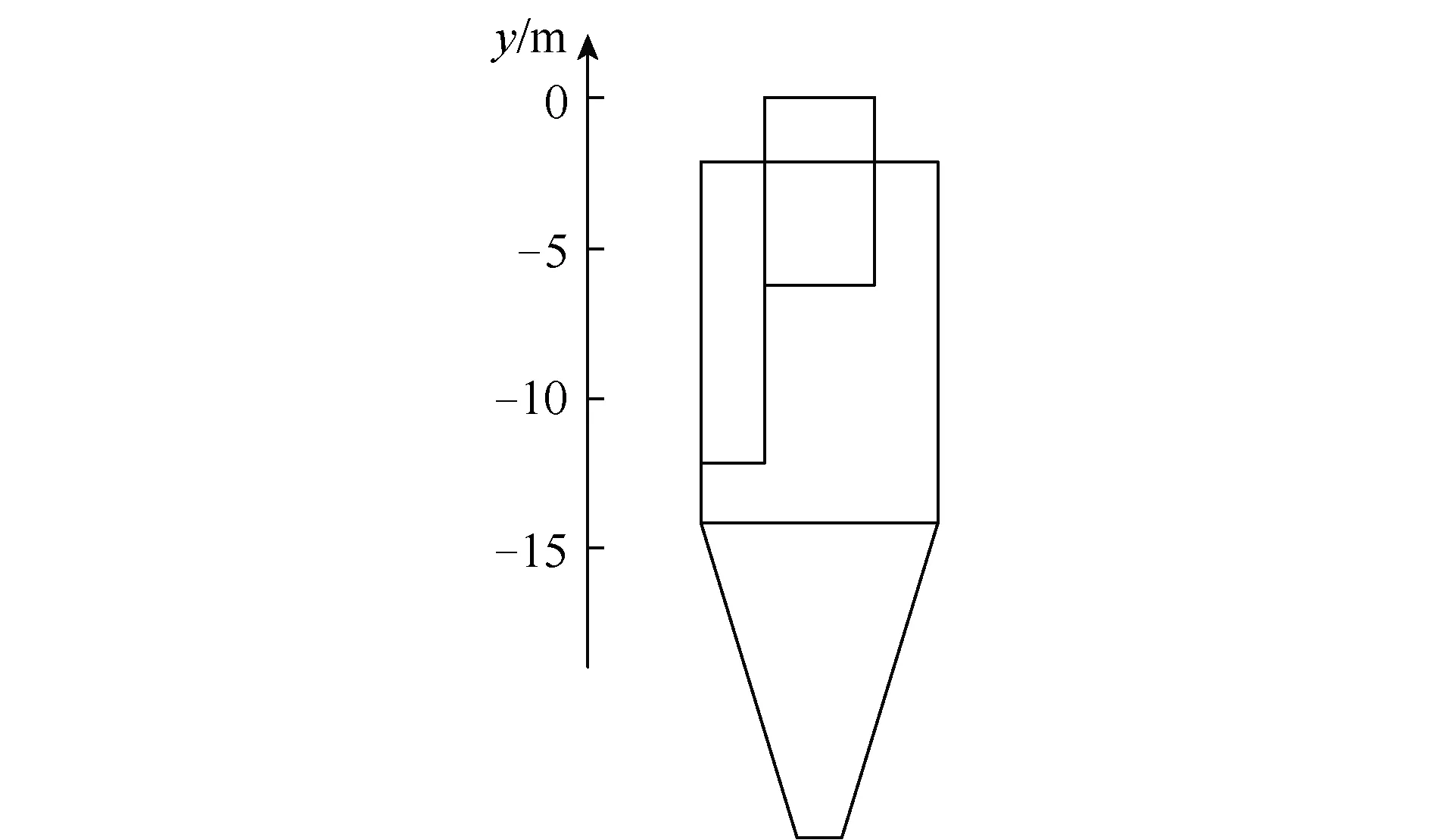
图5 静压分析面分布

分别计算不通入干扰风且入口风速为7.48 m/s时沿竖直高度处6个截面的静压径向分布，如图6所示。

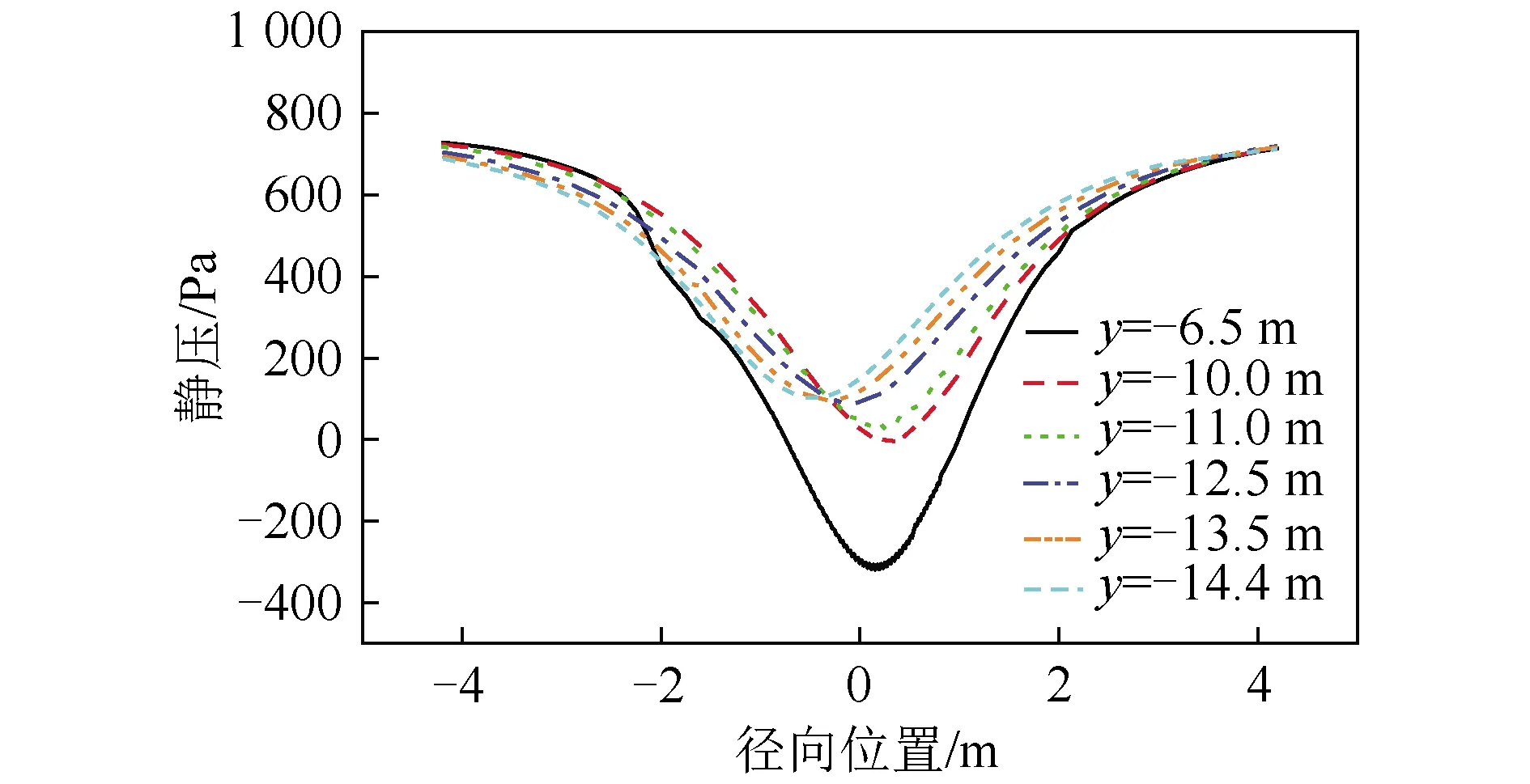
图6 不开孔分离器不同高度径向静压分布

从图6可以发现，静压在旋风分离器内部呈边壁较高、中心较低的分布规律，静压随半径的减少而降低，在中心位置附近达到最低。靠近中心筒的中心位置附近存在较低的负压，这与李强[23]模拟得到的结果一致。此外，不同平面静压分布的最低位置不同，在中心位置两侧各有分布，这与分离器内的静压旋转分布有关(图7)，与张建[10]、李敏[11]等的模拟结果一致。

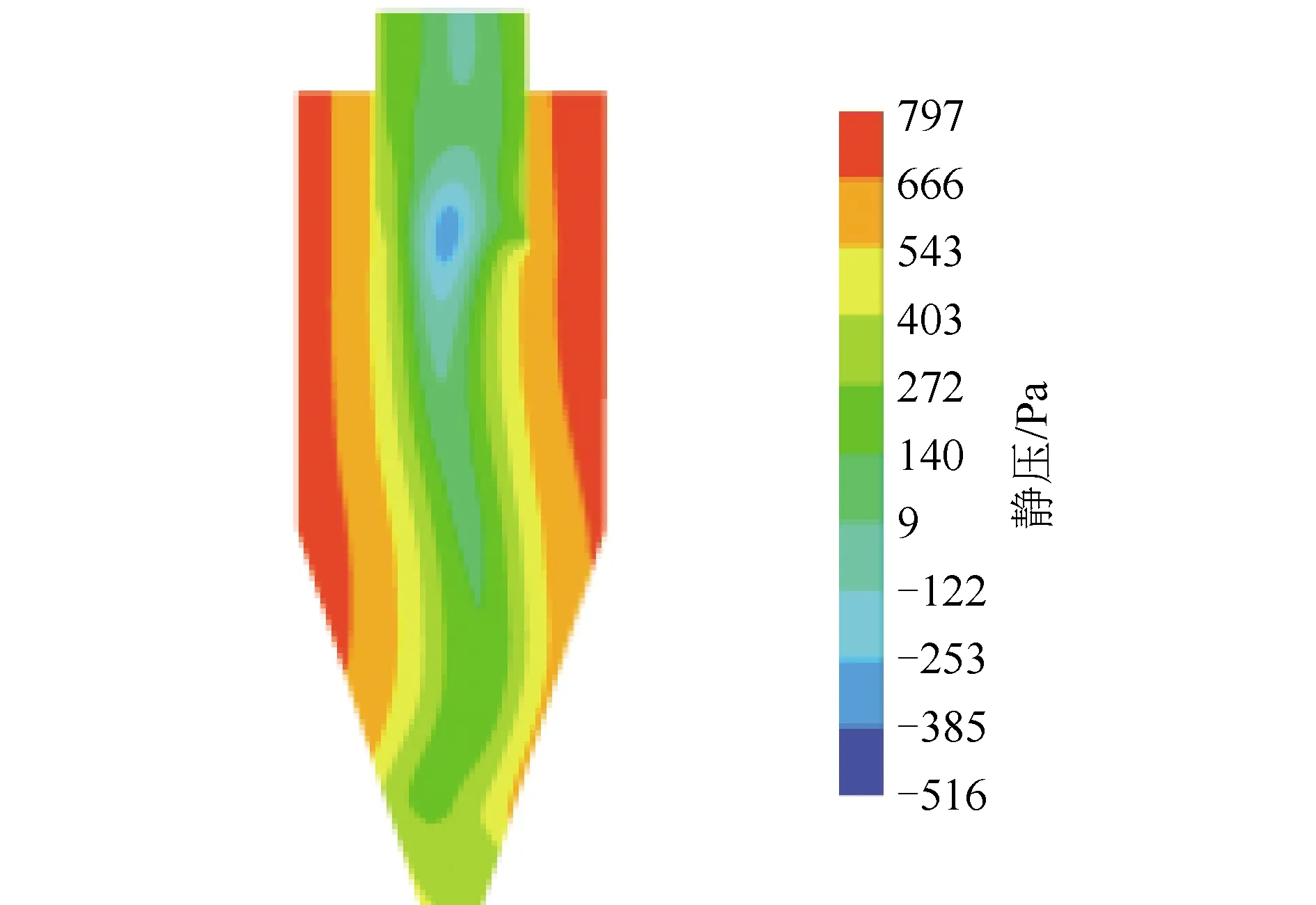
图7 z=0平面静压分布

通入20 m/s干扰风，选取y=-6.5、-11.0、-14.4 m 三个截面，静压分布结果如图8所示。

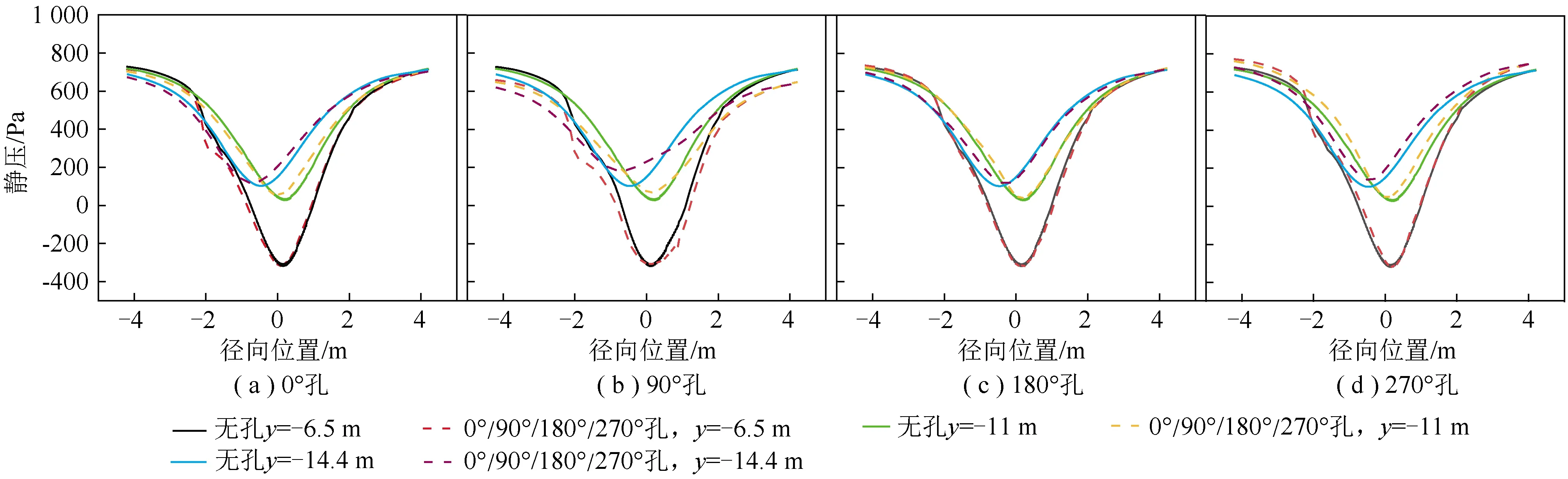
图8 0°孔、90°孔、180°孔、270°孔与不开孔静压分布对比

从图8可以看出，向0°孔、90°孔中通入干扰风后，靠近中心筒入口的-6.5 m平面左侧有一个明显的静压降，其他平面左侧的静压也有所降低。0°孔通入干扰风后选取的3个平面右侧的静压变化较小，而90°孔通入干扰风后选取的3个平面右侧静压降低明显。向180°孔、270°孔通入干扰风后，靠近中心筒入口的-6.5 m平面左侧的静压升高，这与0°孔、90°孔的情况相反。

2.2.2速度分布

开孔平面处竖直分速度如图9所示。可以发现，在开孔平面处上行流主要向0°～90°的区域偏置，在图10中表现更加明显。向4个孔内通入20 m/s干扰风后，轴向速度的分布如图11所示。

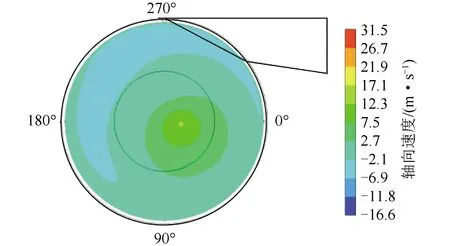
图9 开孔平面竖直分速度分布

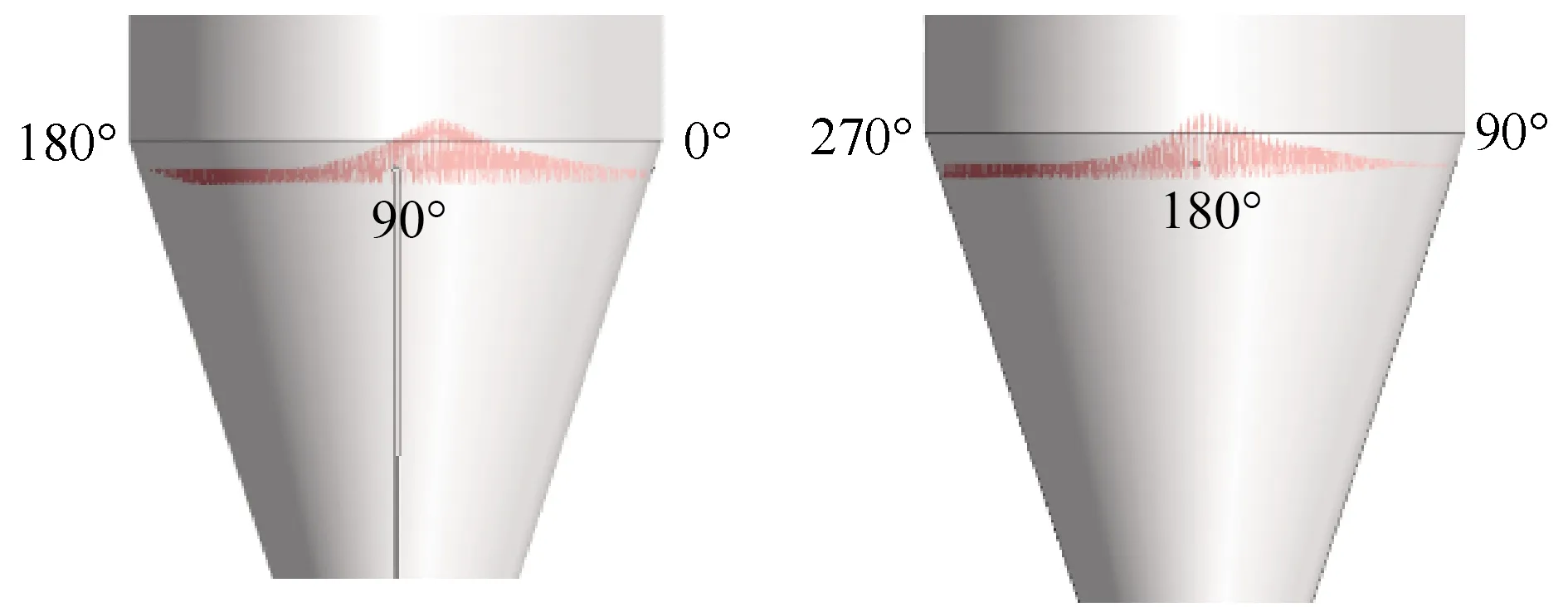
图10 速度竖直分量矢量

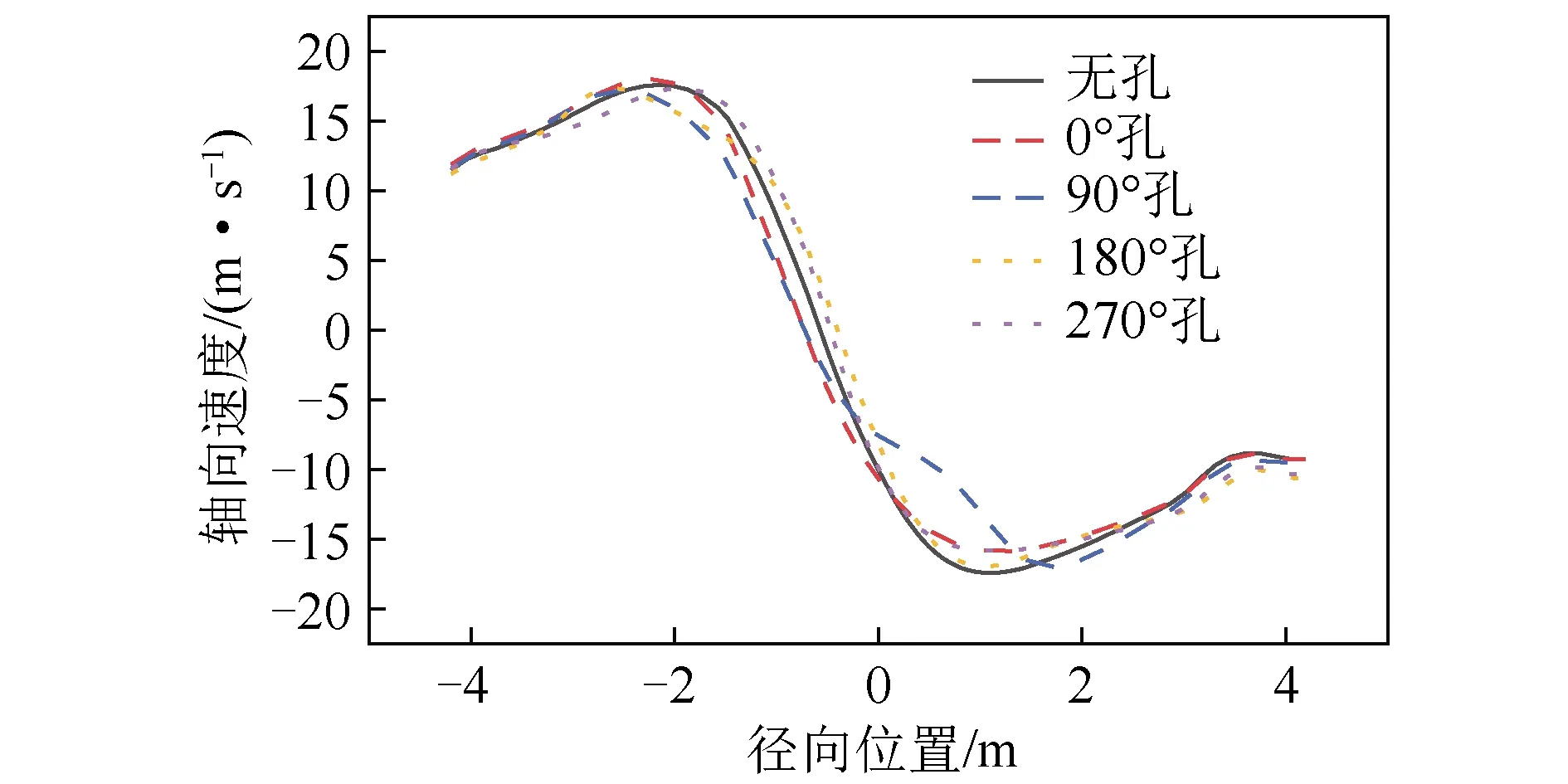
图11 轴向速度分布变化

由图11可知，向4个孔内通入20 m/s干扰风后，旋风分离器入口速度为7.48 m/s。图中左侧对应图12中的0°～90°位置，其上行气流较强。在0°孔、90°孔中通入干扰风后，该位置靠近壁面处的轴向速度增加，而180°孔、270°孔中通入干扰风后该位置靠近壁面处的轴向速度略有降低。

2.3 通入干扰风的压降变化

在文献[1]的基础上研究不通入干扰风旋风分离器在不同入口风速下的压降变化，并与前人的压降经验模型对比。利用同一个网格文件在不同方向的孔进行通入干扰风的计算。分别计算0°、90°、180°、270°孔在通入10、20、30 m/s干扰风的压降，在115 MWe负荷下，对应的入口速度为7.48 m/s。

4个孔通入及不通入干扰风的压降变化规律如图12所示，图中水平线为不通入干扰风且入口速度为7.48 m/s时旋风分离器的压降，虚线为文献[1]中分离效率随干扰风的变化。

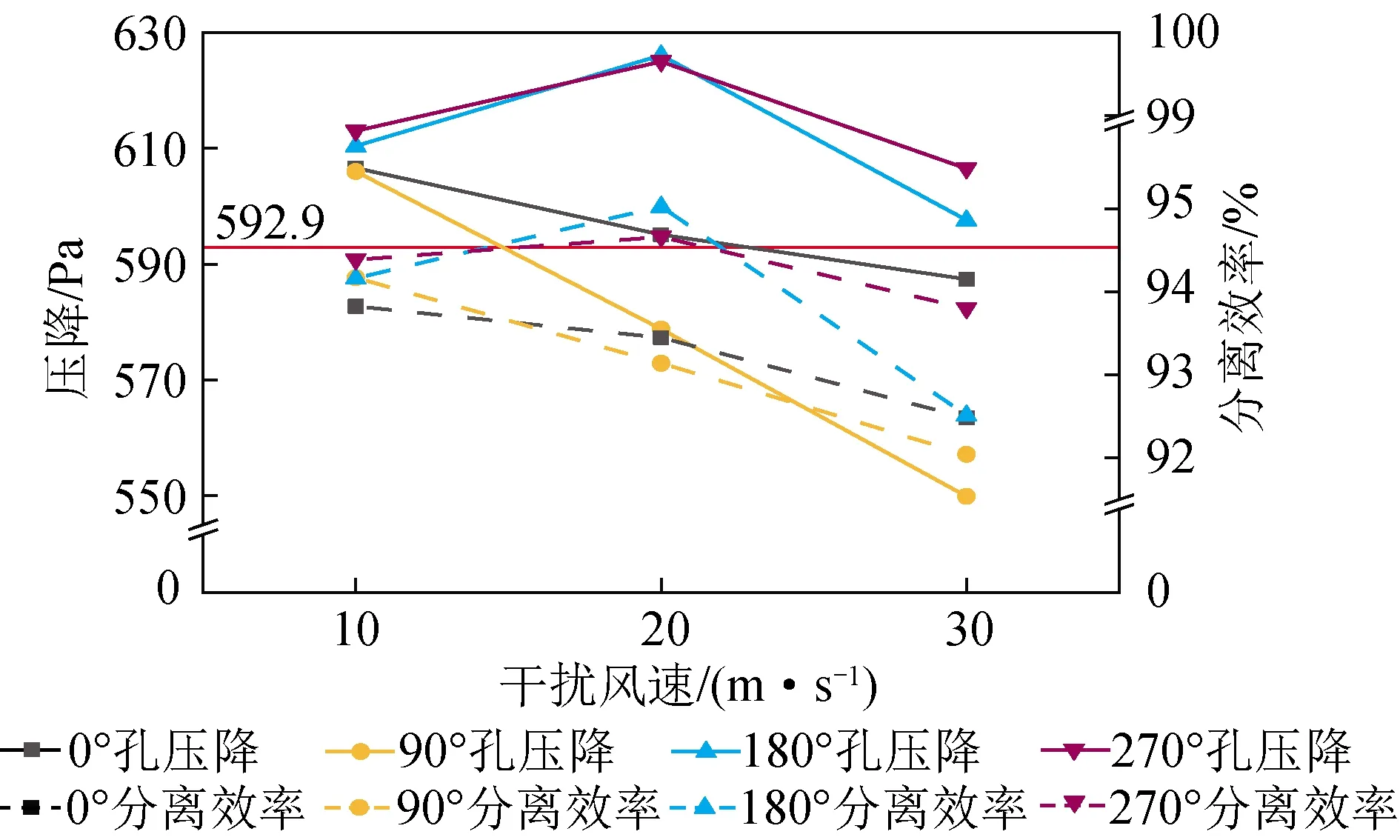
图12 旋风分离器压降及分离效率变化

文献[1]研究结果表明，向0°孔、90°孔通入干扰风后，分离效率随干扰风速的增加而降低；而向180°孔、270°孔通入干扰风后，分离效率随干扰风速的增加先升高后降低。从图12可以看到，0°、90°、180°、270°四个孔中分别通入干扰风后，旋风分离器的压降变化趋势与文献[1]中分离效率的变化趋势相同。向4个孔通入10 m/s干扰风时，旋风分离器的压降差距不大，但均大于不通干扰风时的压降。90°孔通入干扰风后的压降比0°孔通入干扰风下降得快，90°孔通入干扰风能较好地降低旋风分离器压降。180°、270°孔中通入干扰风后的压降变化基本相同。向分离效率可调旋风分离器的4个孔中分别通入10、20、30 m/s干扰风后的压降变化趋势与文献[1]中分离效率的变化趋势大致相同，在文献[1]中90°孔通入干扰风后分离效率变化趋势较好，本文中在90°孔通入干扰风后压降的变化趋势较好。

结合2.2节旋风分离器内部不同高度处静压分布可以发现，靠近旋风分离器入口空间的静压分布变化趋势与旋风分离器的压降变化趋势相同。

2.4 不同工况下密相区温度变化

热力计算研究对象为东方锅炉厂生产的DG1089/17.4-Ⅱ1型亚临界循环流化床锅炉，该锅炉采用单汽包、单布风板、单炉膛、M型布置、平衡通风、一次中间再热、循环流化床燃烧方式，采用高温冷却式旋风分离器进行气固分离。

根据目标机组的结构尺寸和运行数据，针对CFB锅炉进行了耦合炉侧和锅侧的全流程热力计算，热力计算的设计燃料采用电厂提供的入炉煤质报告(表2)。

表2 热力计算设计煤种的元素分析和工业分析

全流程热力计算程序被划分为多个单元模块，主要包括锅炉结构计算模块、燃料计算模块、烟气特性模块、水蒸汽焓值温度计算模块、锅炉热平衡模块和各个相关的受热面换热计算模块，程序的技术路线如图13所示。对于给定的机组发电功率和煤质信息，先假设排烟温度再进行热力计算，当假定排烟温度与计算排烟温度误差<2 ℃时，认为此时热力计算已达到平衡。

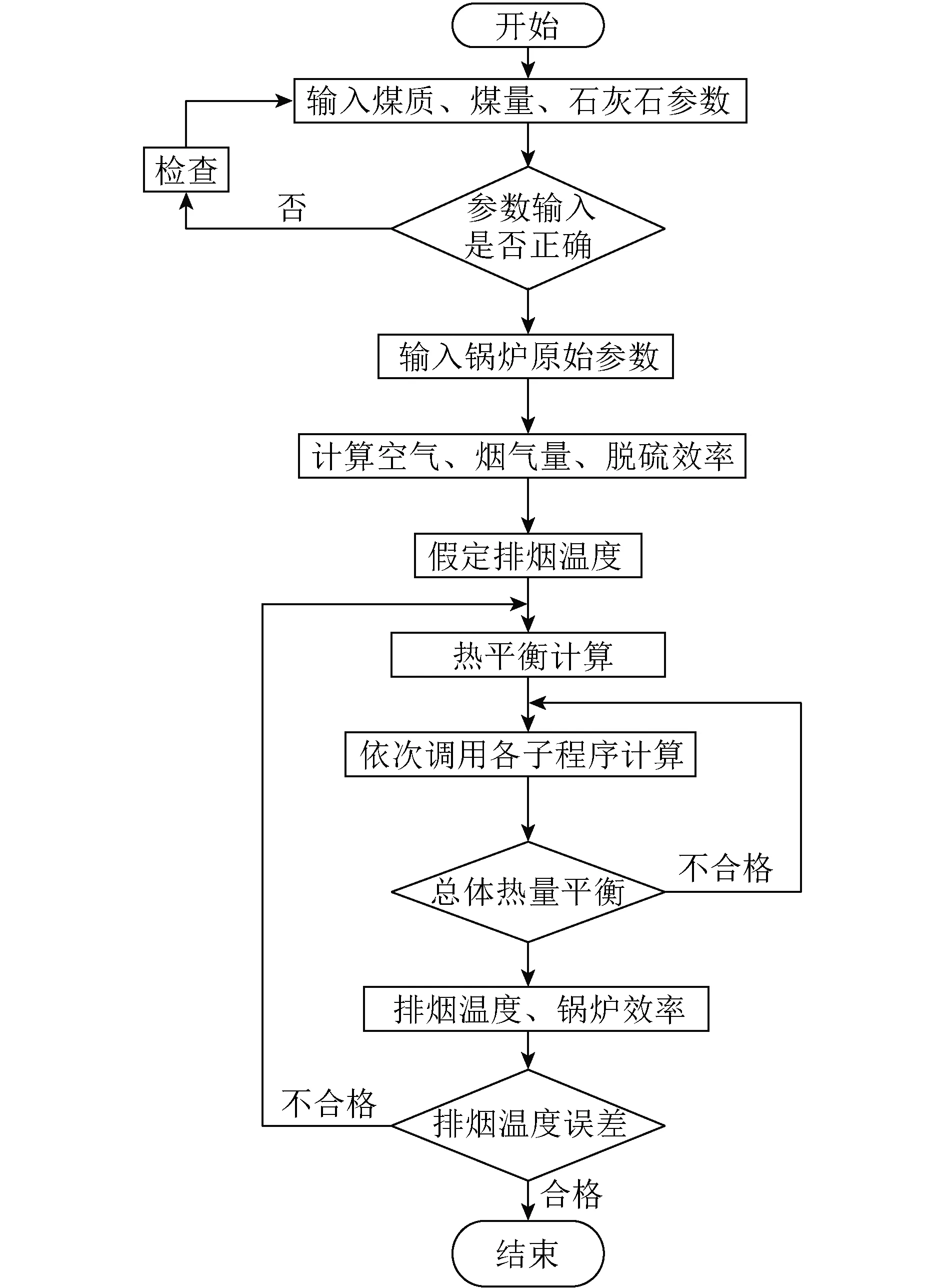
图13 锅炉热力计算程序技术路线

在程序中涉及的换热计算包括各位置的过热器、再热器以及省煤器和空气预热器。受热面的计算流程如图14所示。每个换热面都被设计成一个计算模块，按照汽水流程、烟气流程顺序分别迭代计算，直至每个换热面的计算误差在允许范围内，最后求得合适的排烟温度。对于稀相区受热面，考虑炉内物料浓度变化对传热系数的影响，参考颜勇等[24]的研究，采用颗粒团更新理论对稀相区受热面的传热系数进行计算。

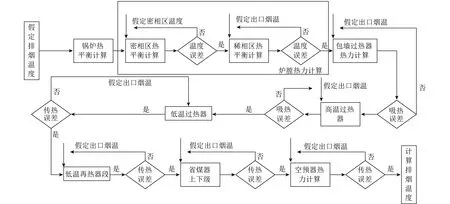
图14 受热面换热计算模块流程

循环倍率的计算公式[25]为

(10)

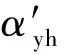
通过改变115 MWe负荷下的旋风分离器的分离效率，研究分离效率改变后循环倍率与密相区床温变化规律，如图15所示。

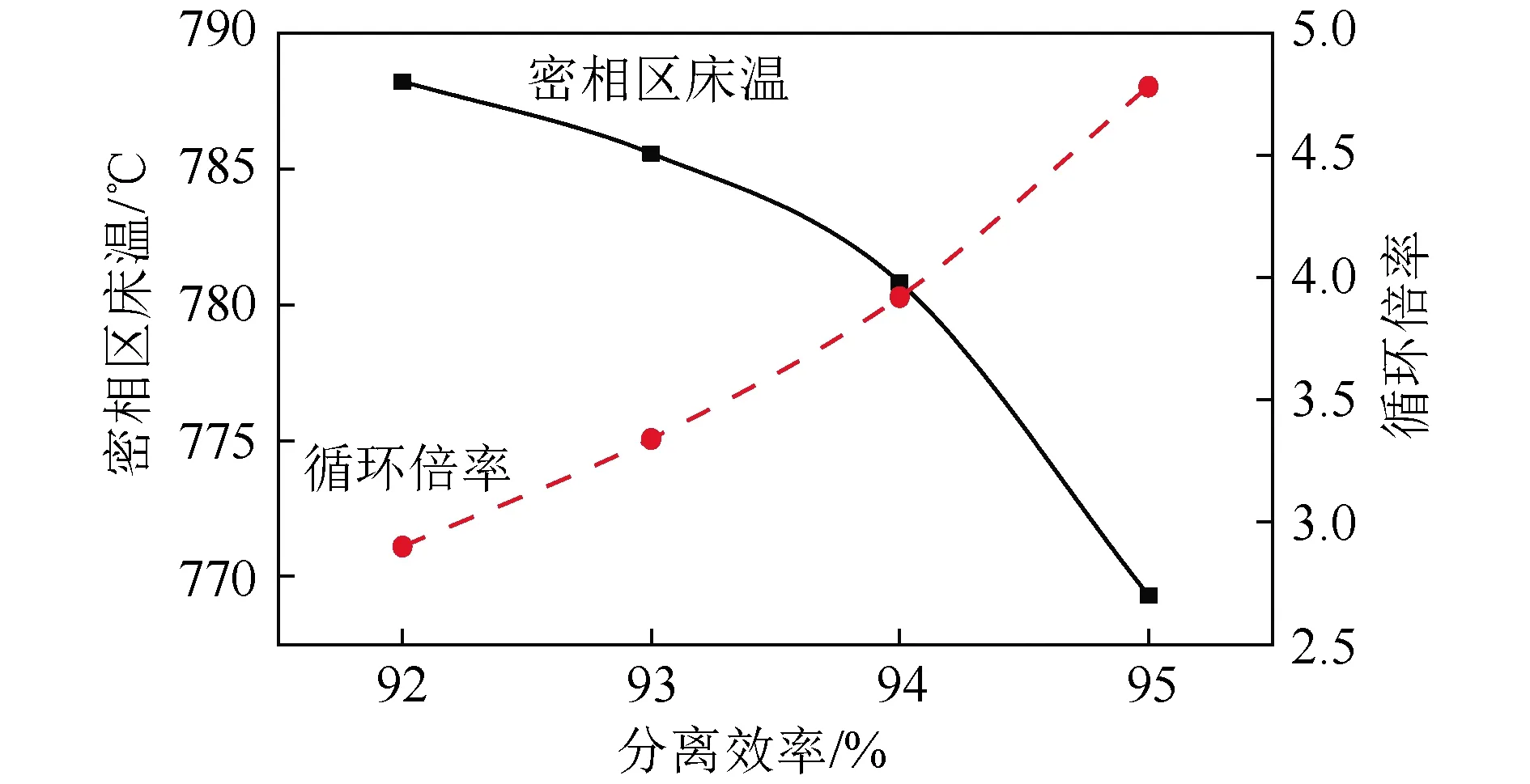
图15 床温与循环倍率随分离效率变化

物料的循环倍率随分离效率的下降而降低，使单位时间内进入密相区的循环灰量和由循环灰带走的热量随之降低，有利于在低负荷下维持锅炉的稳定运行。从图15可看出，分离效率从95%降至92%时，密相区床温可升高19 ℃左右。结合文献[1]，密相区床温随干扰风速的变化如图16所示。

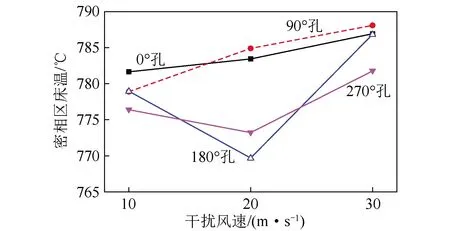
图16 密相区床温随干扰风速变化

由图16可以看出，0°孔、90°孔密相区床温随干扰风速的增加而增加，这与文献[1]一致，且在90°孔通入干扰风对提高密相区床温效果最好。综合分离效率、压降以及密相区的床温变化，本文认为90°孔改造方案为所有改造方案里的最优方案。

3 结 论

1)本文利用雷诺应力模型(RSM)对分离效率可调的旋风分离器进行了压降模拟。未通入干扰风时改变入口流速，将压降模拟结果与压降经验模型计算结果进行对比，发现压降随入口速度的增大而增大，且压降模拟结果与Chen-Shi模型计算结果符合较好。

2)向0°孔、90°孔通入20 m/s干扰风后，靠近分离器入口的空间内静压降低；而向180°孔、270°孔通入20 m/s干扰风后，靠近分离器入口的空间内静压升高，这与此时旋风分离器压降的变化趋势相同。

3)向0°孔、90°孔通入干扰风后，压降随干扰风速的增大而降低；向180°孔、270°孔通入干扰风后，压降随干扰风速的增大先升高后降低。90°孔通入干扰风后的压降降低效果较明显，且在90°孔通入干扰风后密相区床温提升较明显，结合文献[1]中对分离效率的研究，可认为在90°孔处进行改造对旋风分离器优化较好。