基于Barton-Bandis非线性破坏准则的边坡破坏概率分析

2020-12-21陈欢欢刘子航

金属矿山 2020年11期

陈欢欢雍睿刘子航

（绍兴文理学院土木工程学院，浙江绍兴 312000）

边坡稳定性问题涉及到公路工程、水利工程、建筑工程等诸多领域，采用合理有效的边坡稳定性分析方法准确评价边坡稳定性，对于保证人民生命财产安全，确保工程安全有着重要的现实意义。

目前边坡稳定性评价的常用方法可大致分为两类，即定性分析方法和定量分析方法。定性分析方法包括自然（成因）历史分析法、工程地质类比法和图解法等，定量分析方法包括极限平衡分析法（如Bishop 法［1］、Janbu 法［2］、Morgenstern-Prince 法［3］、Spencer法［4］、剩余推力法［5］等）和数值分析法（如有限元法［6］、离散元法［7］、块体理论与不连续变形分析［8］等）。由于传统评价方法存在一定的局限性，国内众多学者在以上两类方法的基础上，引入了一些新的理论方法，如不确定性分析法，其中包括可靠性评价法［9］、模糊综合评价法［10］、灰色系统理论［11］等。目前边坡稳定性分析方法中的理论公式及数值分析多是基于Mohr-Coulomb准则（简称“M-C准则”）。经研究发现，岩体内部广泛分布着结构面，其抗剪强度受粗糙度和壁岩强度的影响呈现非线性特征，当法向应力σn较小时，岩体结构面的抗剪性能并不能充分满足M-C准则［12］。而Barton-Bandis准则（简称“B-B准则”）能够描述岩体内部结构面的非线性力学破坏行为。在估算节理抗剪强度时，B-B准则既能考虑到节理表面的粗糙起伏特征，又能考虑到应力环境及岩壁强度，计算结果较为可靠实用。

根据可靠性设计理论，边坡稳定评价可用概率来表达，而不必用“绝对稳定”或“必然破坏”等结论表示，具体可表示为“具有90%的安全概率”，“90%的破坏可能性”等结论［13］。徐洪［14］以传统边坡稳定性分析中的稳定性系数为基础，结合可靠性理论对边坡稳定进行了常规可靠性分析；陈坤杰［15］通过Bishop条分法进行稳定性分析，建立了边坡的可靠度计算模型，并利用MATLAB编程实现了边坡稳定性的蒙特卡罗模拟计算；张颖［16］运用蒙特卡罗法（Monte Carlo）和Rosenblueth法进行了边坡可靠性分析，有效弥补了传统的边坡稳定性评价方法没有考虑设计参数变异性的不足；张露［17］将瑞典条分法与Monte Carlo法相结合进行了边坡可靠度分析；周超海等［18］将稳定性系数考虑为具有一定破坏概率的随机分布函数，通过蒙特卡罗模拟及Janbu模型对边坡进行了稳定性分析；周春梅等［19］采用Monte Carlo法模拟分析影响边坡稳定性系数的参数分布，在剩余推力法的基础上建立了滑坡破坏概率模型，经过敏感性分析确定了影响边坡破坏概率的主要因素。以上研究在进行边坡稳定性分析时多是将M-C准则作为强度准则。

为更好地适应岩体结构面抗剪强度所呈现的非线性特征和抗剪强度参数的离散性特征，本研究基于B-B准则的边坡破坏概率分析方法，建立了岩质边坡稳定性分析模型，对最危险滑动面进行破坏概率分析，并将改进的破坏概率分析方法与传统极限平衡分析法的计算结果进行对比分析，验证基于B-B准则的边坡破坏概率分析方法评价边坡稳定性的有效性。

1 基于B-B准则的边坡破坏概率分析法

基于B-B准则的边坡破坏概率分析方法是在非线性B-B准则的基础上选用表征岩体结构面特征的3种抗剪强度参数及其分布来建立岩质边坡稳定性分析模型，结合Monte Carlo法和各参数分布生成多组随机数，通过Morgenstern-Price法（简称“M-P法”）对边坡岩体内部潜在的滑移面进行稳定性分析，得到潜在滑移面上的多组稳定性系数，采用Monte Carlo法对多组稳定性系数进行统计分析，确定边坡稳定性系数均值和破坏概率。

1.1 结构面抗剪强度参数选取

BARTON等［20］等在研究多组结构面的直剪特性和试验结果的基础上，提出了用于估计不规则、无充填结构面峰值抗剪强度的非线性JRC-JCS经验公式：

式中，τ为结构面抗剪强度，MPa；σn为作用于结构面上的法向应力，MPa；ϕb为基本摩擦角，（°）；JRC为结构面粗糙度系数；JCS为结构面壁岩强度，MPa。

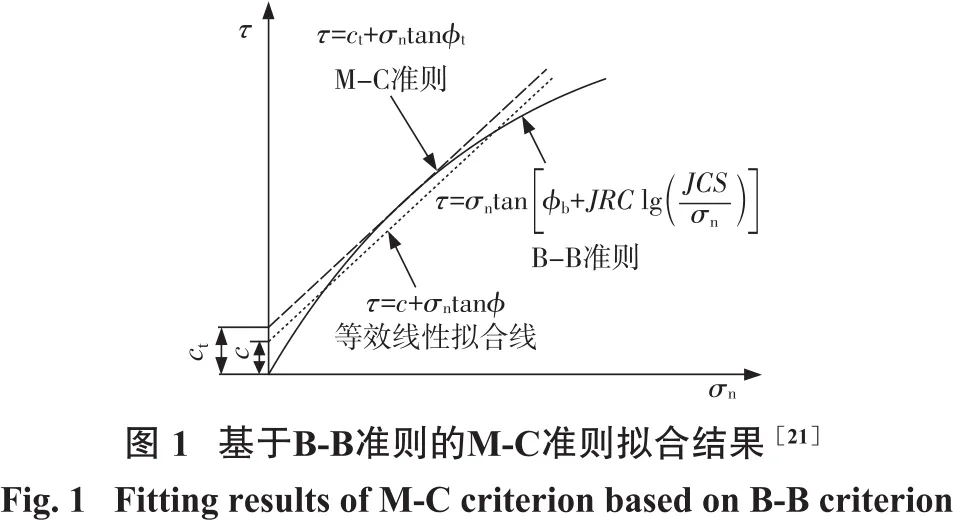
M-C准则与B-B准则对比如图1所示。图1中，c为结构面黏聚力，ϕ为结构面内摩擦角，ct为结构面等效黏聚力，ϕt为结构面等效内摩擦角，两者可由BB准则等效线性拟合M-C准则得到。考虑到M-C准则的局限性，本研究选取非线性JRC-JCS经验公式中的JRC、JCS、ϕb等作为边坡岩体结构面的特征参数进行边坡建模。

1.2 稳定性系数计算

M-P法在进行边坡稳定性分析时不仅考虑了条块之间力的平衡和力矩的平衡，而且考虑了滑动岩体的边界条件，可对非圆弧滑动面上可能滑动的岩体中微分条块列出同时满足力与力矩平衡条件的微分方程式。假定每一条块切向条间力T与法向条间力E之间存在一个对水平坐标x的函数关系：

式中，λ为条间力比例常数；T为每个条块的切向条间力，kN；E为每一条块的法向条间力，kN。

于是，每一条块两侧的边界条件为

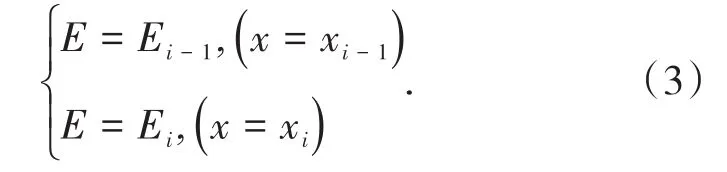
边坡整体力平衡稳定性系数Ff和力矩平衡稳定性系数Fm可分别进行如下计算［22］：

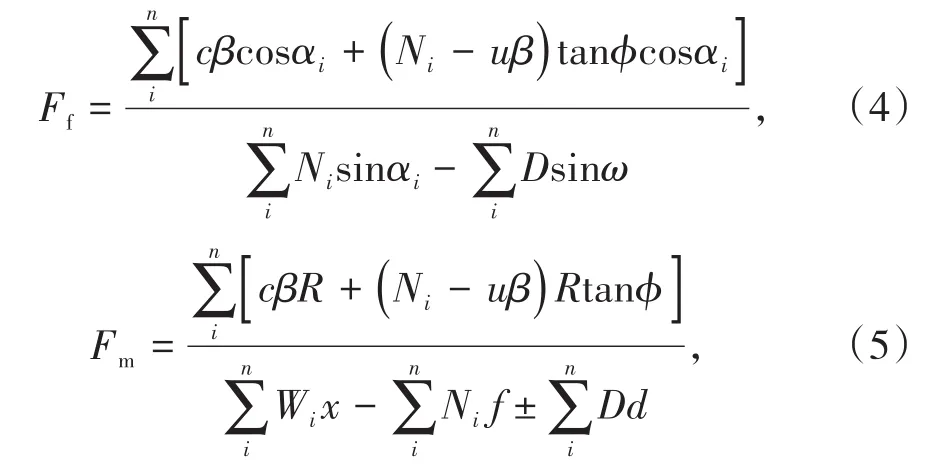
式中，c为结构面黏聚力，kPa；ϕ为结构面内摩擦角，（°）；Wi为滑体各条块的重力，kN；u为孔隙水压力，kPa；Ni为条块底部法向力，kN；D为集中荷载，kN；ω为集中荷载与竖直方向的夹角，（°）；αi为滑体底面倾角，（°）；R为滑弧圆心到滑弧的距离，m；x为水平坐标；f为摩擦系数；d为集中荷载的力矩，kN·m；β为折算系数；i为滑体各条块编号，1≤i≤n。

结合边界条件及微分方程的迭代计算，求得Ff和Fm随λ变化的分布曲线，两分布曲线的交点即为稳定性系数Fs。由于微分计算过程较繁琐，故使用SLIDE软件中的M-P法模块进行计算和分析。

1.3 破坏概率计算

Monte Carlo法又称随机模拟法或统计试验法，是边坡可靠性分析时常采用的一种方法。影响稳定性系数的各种参数（如JRC、JCS、ϕb等）在获取过程中会因外界因素或人为因素的作用而产生随机性误差，这些参数从严格意义上可以看作随机变量。稳定性系数Fs可看作随机变量JRC、JCS、ϕb的状态函数，其函数表达式为

若已知状态变量JRC、JCS、ϕb的概率分布，根据边坡的极限状态条件Fs=0，利用Monte Carlo法产生符合状态变量概率分布的3组随机数(JRC1,JRC2,…,JRCn)，(JCS1,JCS2,…,JCSn)，，并将其代入状态函数（式（6））计算得到状态函数Fs的y个随机数。如果在这y个随机数中有x个小于或等于1（以稳定性系数表示边坡状态），当y足够大时，根据大数定律，此时的频率已近似于概率，因而可得到边坡的破坏概率：

2 工程实例

2.1 矿山概况

柏杨庙矿山位于贵州省遵义市桐梓县娄山关镇沙嘴村，中心点地理坐标为东经106°49′55.20″，北纬28°6'28.80″。研究区位于黔北山地与四川盆地的衔接地带，冰川作用显著，溶蚀侵蚀并存，长期的地质作用使岩体结构多呈现层状结构。研究区地处中亚热带高原季风湿润性气候区，年平均降雨量1 038.8 mm，夏季降水量多，冬季降水量少。勘查期间未发现该矿山附近存在地表水系，矿山开挖面也未见地下水溢出。该区不处于地震带，属于弱震环境，根据中国地震烈度区划，区内为Ⅴ度区。矿山边坡整体轮廓如图2所示。该边坡近NE走向，倾向SE。总体边坡高度100 m，宽度145 m，进深100 m，坡向137°，坡角75°，无台阶边坡。边坡整体主要出露石灰岩，以发育层面、节理为主，边坡范围内没有断层发育，自然容重为27 kN/m3，饱和容重为28 kN/m3。层面B1产状132°∠66°，规模120 m，无填充物。边坡发育两组节理J1、J2，其中节理J1产状54°∠38°，规模0.2～1 m，间距0.1～0.6 m，无充填物；节理J2产状225°∠73°，规模0.8～2 m，间距0.1～0.4 m，无充填物。经调查，没有发现该边坡岩性、构造、工程地质和水文地质条件存在明显变化的情况。

2.2 滑移面确定

该矿山边坡潜在滑移面可采用露天矿山边坡稳定性分级分析法确定［23］。通过对层面B1与总体边坡坡面进行赤平投影（图3）可知，层面（贯穿性结构面）控制着边坡的整体稳定性。总体边坡坡向137°，坡角75°。层面B1倾向132°，倾角66°，层面倾向与边坡倾向夹角5°，小于30°，为顺坡向层面，且层面倾角（66°）小于边坡坡角（75°），边坡整体很有可能沿该结构面发生单平面型滑移破坏，故需对总体边坡进行稳定性评价。

2.3 结构面统计测量与数据分析

依据赤平投影分析结果，在层面B1的作用下，该边坡整体有可能沿该结构面发生单平面型滑移而产生破坏，层面B1为潜在滑移面。因此，需要对层面B1开展结构面取样调查。

2.3.1JRC统计测量与取值

在潜在滑移面所对应的结构面上，使用轮廓曲线仪绘制了106条结构面轮廓曲线（图4）。采用工程高清扫描仪扫描结构面轮廓曲线图，将图中曲线转换为图片格式文件，通过计算程序对图中曲线进行异常点排除、形态学滤波去噪和图像归一化，提取扫描图片的灰度值矩阵。根据结构面实测长度与数字化灰度矩阵的大小关系，将轮廓曲线上各像素点坐标转化为实际坐标数据，采用全域搜索法在每条轮廓曲线上提取10 cm的试样，分别读取并存储每条轮廓曲线10 cm试样的坐标数据。本研究通过杜时贵［23-24］所提出的Barton直边法的简明公式计算每条结构面试样的JRC：

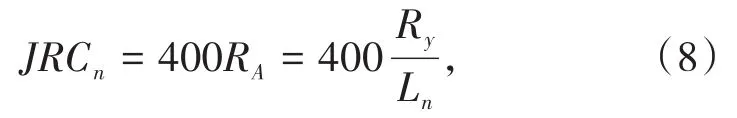
式中：RA为相对幅度；Ln为轮廓曲线长度，cm；Ry为结构面表面轮廓曲线齿凸幅度，cm。

2.3.2JCS统计测量与取值

本研究采用回弹法确定JCS值，选用指针直读式回弹仪在潜在滑移面所对应的结构面上测量了48组回弹值（图5），依据回弹值与壁岩强度关系和壁岩状态（含水、风化情况），确定结构面壁岩强度大小［23］。为方便起见，基于MATLAB软件程序计算JCS值。首先输入岩石容重、回弹值及结构面真倾角；然后设定曲线选型范围、容重范围、坐标转换参数及强度插值参数；最后输入回弹参数进行坐标转换，进行强度计算、偏差分析，确定JCS值和饱和状态回弹值。

2.3.3 ϕb取值

将回弹值代入基本摩擦角的经验公式，即理查兹提出的结构面回弹值与基本摩擦角的线性关系式［25］，得到ϕb：

式中，N为回弹值。

2.4 抗剪强度参数统计分布检验

2.4.1 概率密度函数

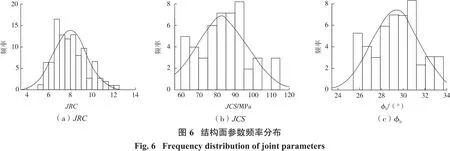
在进行边坡稳定性分析之前，需要验证参数的概率分布。各参数的频率分布如图6所示。由图6可知：各参数分布图形与正态分布函数图形相似，可对3组数据分别进行正态分布检验。

2.4.2 K-S检验

由图6可知：样本数据概率分布的拟合程度与正态分布相近，但精确检验还需要通过数量方式实现，可选择单样本K-S检验法检验样本数据是否服从某种理论分布。检验结果如表1所示。正态分布形式的双尾概率P（JRC）=0.052>0.05，P（JCS）=0.2>0.05，P（ϕb）=0.2>0.05，表明三者均接受该形式假设。因此，JRC、JCS、ϕb的样本数据均符合正态分布特征的假设。

2.5 边坡稳定性分析

2.5.1 基于B-B准则的边坡破坏概率分析

2.5.1.1 边坡模型及荷载设定

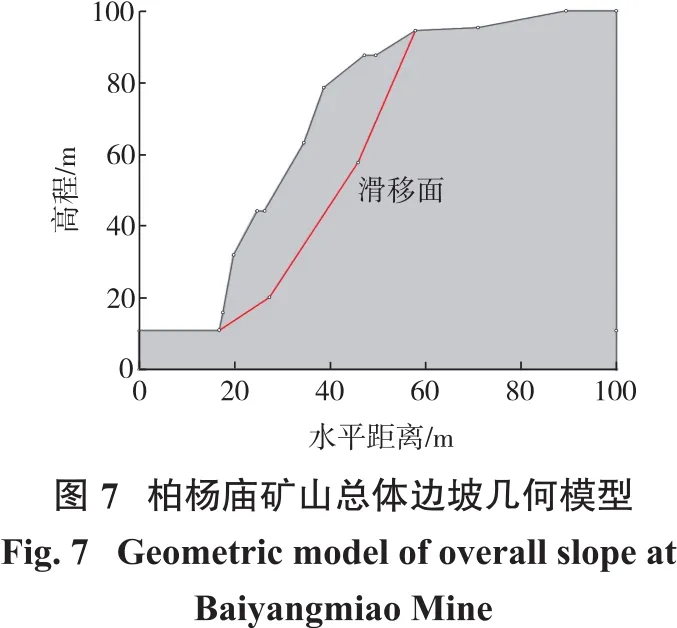
按照矿山边坡所对应的原型几何尺寸建立的分析模型如图7所示。该边坡为自然边坡，根据《建筑抗震设计规范》（GB 50011—2010）［26］要求，可不考虑地震作用，边坡表面没有任何外部荷载，周围没有明显的水文地质条件，故模型表面不需设置荷载，可不考虑地下水的渗流作用，但需考虑降雨的影响。降雨工况下，岩体内部水、气两相压力变化导致岩体结构面抗剪强度参数发生变化，故需对降雨工况下的抗剪强度参数作适当折减处理［27］。

2.5.1.2 强度模型及参数设置

本研究选用B-B准则作为稳定性计算的强度准则，所采用的计算参数为JRC、JCS、ϕb，将三者在干燥状态和饱和状态下的平均值、标准差、相对最小值及相对最大值分别导入模型，基本数据如表2所示。JCS在饱和状态下的样本数据可通过软化系数k=0.7对干燥状态的样本数据进行折减获得［28］，ϕb在饱和状态下的样本数据可根据2.3.2节确定的饱和状态回弹值代入式（9）计算获得。

2.5.1.3 模拟过程

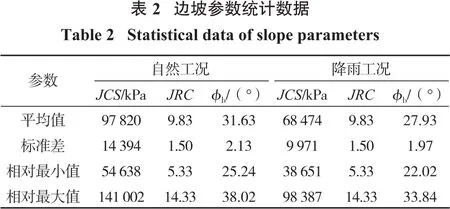
注：表中各参数样本数据均符合正态分布。

本研究采用M-P法来计算边坡稳定性系数，模拟方法为Monte Carlo法，滑动方向为从右向左，迭代计算次数小于50次，滑动面类型为非圆弧型滑动。在模型中预先设置好潜在滑动面，根据参数统计数据，采用Monte Carlo法进行随机抽样，在考虑计算精度的前提下，选择模拟次数为1 000次［29］，选用自动搜索方式对每一组参数随机样本值进行最不利滑裂面搜索，分别求得总体边坡在自然工况、降雨工况下的多组稳定性系数，采用Monte Carlo法统计分析稳定性系数值，确定边坡破坏概率。

2.5.1.4 计算结果分析

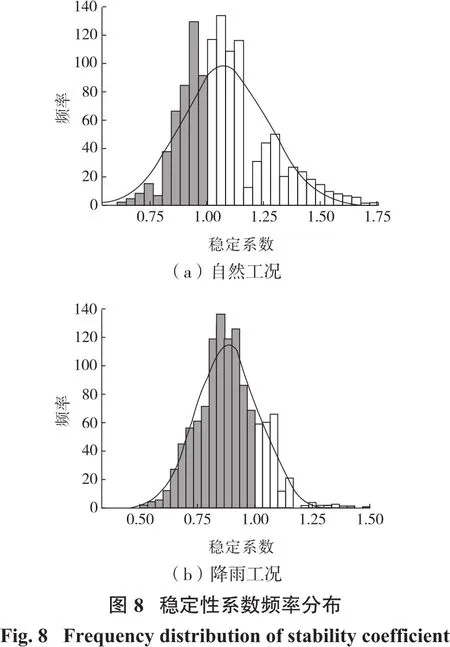
经过模拟计算，得到两种工况下各1 000组稳定性系数值，对其进行统计分析，得到稳定性系数的频率分布（图8），图中灰色部分为Fs<1。不同工况下的计算结果如图9所示，图中PF为边坡破坏概率。自然工况下，稳定性系数服从正态分布，其最大值为1.683，最小值为0.619，平均值为1.029，破坏概率为49.424%。降雨工况下，稳定性系数服从正态分布，其最大值为1.438，最小值为0.561，平均值为0.875，破坏概率为83.852%。根据稳定性等级划分标准［30］判断，自然工况下的边坡处于中等危险状态，稳定等级为3；降雨工况下的边坡处于高危险状态，稳定等级为2。

2.5.2 基于传统极限平衡分析法的边坡稳定分析

2.5.2.1 基于B-B准则的极限平衡分析

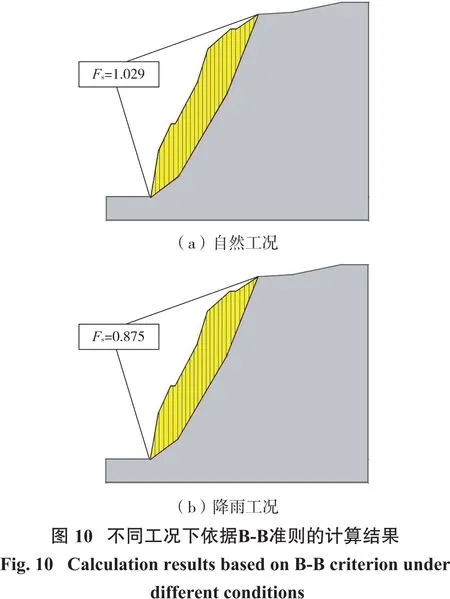
基于B-B准则的极限平衡分析法进行边坡稳定性分析时选用JRC、JCS、ϕb的平均值作为边坡稳定性分析参数。将两种工况下各参数的平均值分别导入基于B-B准则的边坡模型，采用M-P法计算得到两种工况下的稳定性系数（图10）。自然工况下，边坡的稳定性系数为1.029，大于1小于1.05；降雨工况下，边坡的稳定性系数为0.875，小于1。根据《滑坡防治工程勘查规范》（GBT 32864—2016）［31］，该边坡整体在自然工况下处于欠稳定状态，在降雨工况下处于不稳定状态。

2.5.2.2 基于M-C准则的极限平衡分析

（1）法向应力取值。由野外地质调查可知，桐梓县地区地质构造稳定。因此，可按式（10）来计算边坡垂直方向主应力和水平方向主应力［32］：

式中，H为滑体高度，m；γ为结构面上覆岩石容重，（×10-3MN/m3）；σV为结构面所处部位垂直主应力，MPa；σH为结构面所处部位水平主应力，MPa。

在已知垂直主应力和水平主应力的情况下，可通过矢量法计算获得结构面上的法向应力，选取5个试算点1/3σn、2/3σn、σn、4/3σn和5/3σn。

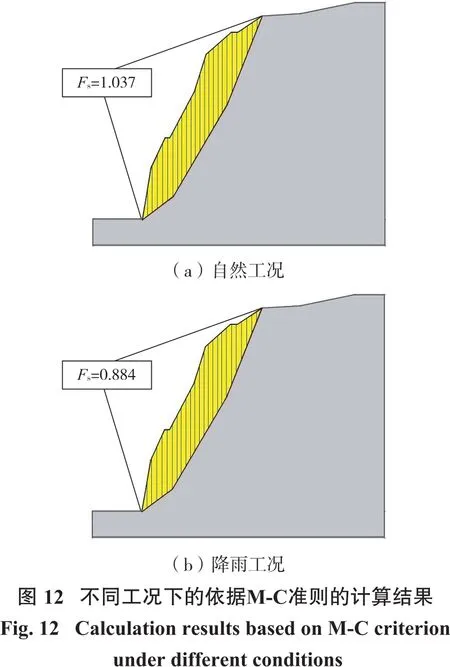
（2）稳定性系数计算。将试算的5个法向应力值和JRC、JCS、ϕb的平均值分别代入式（1）得到多组抗剪强度值，结果如表3所示。根据记录结果，以最小二乘法进行线性拟合，结果如图11所示。由直线的倾角确定岩体结构面自然工况下的峰值内摩擦角ϕ=40.59°，降雨工况下的峰值内摩擦角ϕ=35.42°；由直线的截距确定结构面自然工况下黏聚力c=0.541 2 MPa，降雨工况下黏聚力c=0.456 8 MPa。将两种工况下的峰值内摩擦角和黏聚力分别导入基于M-C准则的边坡模型，采用M-P法计算得到两种工况下的稳定性系数。

（3）计算结果分析。极限平衡分析法的计算结果如图12所示。自然工况下，边坡的稳定性系数为1.037，大于1小于1.05；降雨工况下，边坡的稳定性系数为0.884，小于1。根据《滑坡防治工程勘查规范》（GBT 32864—2016）［31］，该边坡整体在自然工况下处于欠稳定状态，在降雨工况下处于不稳定状态。

2.5.3 计算结果对比分析

通过上述两类方法对岩质边坡进行稳定性分析，发现其计算结果与所采用的强度准则密切相关，在计算方法相同的前提下，不同的强度准则可以求解出不同的稳定性系数。传统极限平衡分析法以线性M-C准则作为强度模型进行边坡稳定性分析时，天然节理的粗糙度和壁岩强度的影响使M-C准则不再适用于岩体结构面非线性破坏的情况，故计算结果存在一定的误差；以非线性B-B准则作为强度模型时，尽管适用于岩体结构面抗剪强度的非线性特征，但仅以稳定性系数来评价边坡稳定性不够精确。基于B-B准则的破坏概率分析方法以非线性B-B准则作为强度模型，考虑到了岩体结构面抗剪强度的非线性特征，所采用的抗剪强度参数获取方便，以多种随机变量的统计分布特征为基础进行建模，避免了抗剪强度参数离散性的影响，计算结果以稳定性系数和破坏概率形式来表达可靠性较强。