基于立体视觉的无人机动态目标实时跟踪

唐 凯，张海涛，郑建杰，孔维迪

(陆军工程大学 国防工程学院，江苏 南京 210000)

0 引言

对空中动态目标的跟踪是实现无人机协同工作的基础，也是当前无人机技术领域研究的前沿课题之一。单目相机无法提供目标深度，使用限制较多，双目相机根据三角测量原理可以直接计算目标的空间位置，适用范围更广[1]。TEULIERE C[2]等人使用搭载俯视单目相机的四旋翼飞行器，跟踪地面模型赛车，由IMU 计算飞行器高度，实现了对目标的航向角锁定与跟踪定位。MIGUEL[3]等人使用搭载前视单目相机的四旋翼飞行器，跟踪红色气球，通过特征面积计算相对距离，使用模糊控制实现了目标定位跟踪。

张梁等人[4]利用双目相机测量目标的空间位置，实现了六旋翼飞行器对目标的跟踪。

TEULIERE C[2]、MIGUEL[3]、张梁等人[4]实现的目标跟踪是基于颜色的特征跟踪Camshift[5]算法，该算法的跟踪窗口可根据目标实时缩放，跟踪定位效果较好，但该算法只适用于光照恒定的室内环境以及背景色彩单一的室外环境。

本文提出了一种基于轮廓的特征跟踪方法，连续自适应椭圆检测(Continuously Adaptive Ellipse Detector，CAED)算法，克服了特征跟踪Camshift 算法过于依赖色彩的缺陷，降低了复杂室外环境下目标丢失的几率，提高了目标检测的适用范围。文中提出的对空中动态目标跟踪算法，通过在四旋翼飞行器上搭载双目相机，并自行设计四旋翼飞行控制算法，实现对空中动态目标的平稳跟踪。对于无人机协同工作以及无人机电力巡检、除障等有一定的参考意义。

1 基于视觉的目标跟踪

为了实现无人机基于双目相机的动态目标跟踪，主要步骤可分为：(1)四旋翼无人机在平稳起飞后，读取相机图像，利用CAED 算法识别目标；(2)利用双目测距算法，计算目标的位置；(3)针对目标追踪，建立四旋翼控制模型。

1.1 CAED 目标跟踪算法

CAED 算法基于目标的轮廓，实现在每帧对目标的识别与跟踪。CAED 以椭圆检测（Ellipse-Detector，ED）算法为核心，实现图像任一时刻的ED 迭代计算，再以此帧得到的目标窗口为下一时刻ED 算法搜索窗口的初始值，可以在每一帧都快速检测到目标物体的像素中心。

1.1.1 ED 算法

ED 算法是FORNACIARI M[6]等人提出的一种快速椭圆检测算法，可以在嵌入式设备实时运行。该算法是一种基于边界聚类的椭圆检测方法，结合使用了基于弧段的方法和最小二乘法。从边界图提取圆弧，再经过过滤、聚类，最终用最小二乘法拟合出椭圆。总体程序如图1 所示。该方法能有效应对多个椭圆、椭圆相互遮挡和椭圆部分缺损等复杂情况。图2 显示了ED 算法的椭圆检测结果(圆心与外形皆已标出)。

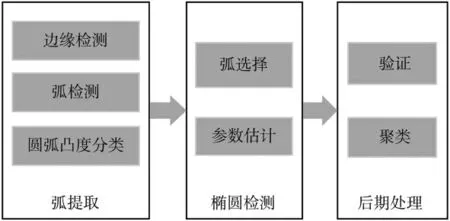
图1 椭圆检测总流程

图2 椭圆物体检测结果

1.1.2 CAED 算法

单纯的ED 算法足以在图像中可靠地检测出椭圆物体，但是由于其是在全图检测并验证，计算耗时相对较长，无法在微型计算机上达到60 fps 的实时性要求。

受到Camshift[5]算法的启发，CAED 算法充分利用前后多帧与左右两帧图像椭圆目标的像素中心之间的约束关系，从而设置合适椭圆搜索窗口，既提高了目标检测的速度，又提高了双目测距的可靠性和实时性。CAED 算法的迭代计算过程如下：

(1)初始化。针对目标大小，设定检测椭圆像素半径阈值，左目相机从全图搜索椭圆目标，如果检测到目标，标记其中心位置和轮廓，设定搜索窗口为同心矩形，边长为椭圆长径的3 倍。

(2)预估相邻帧搜索窗口。假设相邻3 帧目标与相机的距离变化率、位置变化率方向都不变，由左帧中目标的位置，推算右帧和下一左帧的初始搜索窗口。

(3)检测目标。在(2)预估的窗口(图3 虚线框)中检测椭圆目标，计算中心和半径。

(4)重置搜索窗口。使用(3)的结果，重新设置窗口中心和大小(图3 实线框，箭头为目标在图像中的运动方向)，并作为下一帧的初始搜索窗口。

(5)重复步骤(2)～(4)，如果丢失目标，就再次执行步骤(1)。

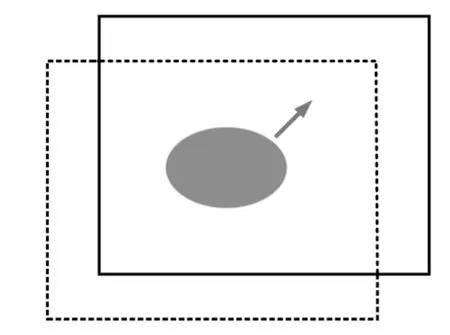
图3 前后帧搜索窗口迭代过程

在高帧率相机的配合下，CAED 可以对目标轨迹作合理预测，并根据目标在视野中的位置与大小自动调整搜索窗口，保证了实时性。

1.2 双目测距

1.2.1 相机标定

双目测距算法根据目标在左右相机的像素坐标，利用三角测量原理计算目标的空间位置。由于出厂时相机的参数一般是未知的，因此，需要事先标定双目相机。

标定后可以得到左右相机的内参数K1和K2，以及外参数(左右相机的相对位姿)R、t。本文采用具有较好的鲁棒性和实用性的张氏标定法[5]计算内参K1和K2，在此基础上，利用对极几何和单应矩阵H 分解得到外参R、t。

(1)内参标定

设相机坐标系下的空间点p=(x，y，z)T(见图4)，投影点像素坐标puv=(u，v，l)T可表示为：

其中K 为相机的内参数矩阵。

图4 针孔投影模型

(2)外参标定

外参标定本质上是计算左右相机投影平面的相对位姿，根据对极几何约束(图5)，由至少8 对正确匹配的像素点(p1，i，p2，i)可以推断相对位姿。

图5 对极几何约束

特别注明，当像素点p1，i共面和p2，i共面时(如棋盘格角点共面)，可以利用单应矩阵H 描述像素点的匹配关系：

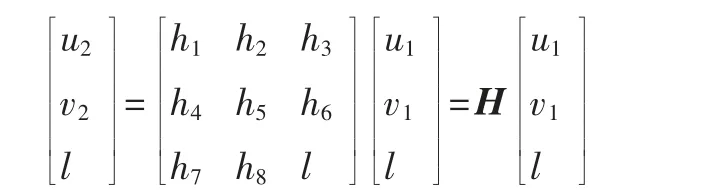
利用直接线性变换求得H，再对其作SVD 分解，得到外参R、t。

1.2.2 双目测距

双目相机的内外参数确定后，就可以由三角测量(图6)原理求得目标的空间位置。O1和O2为光心，p1和p2为匹配的像素点。理论上，直线O1p1与O2p2会相交于点p，该点即为相应的空间点。

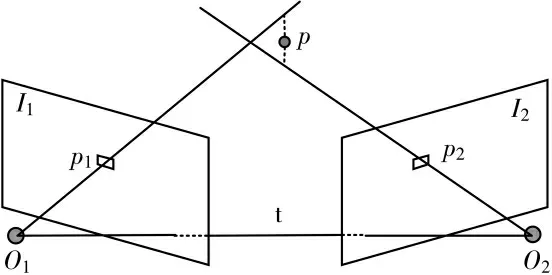
图6 由三角测量计算地图点深度

由对极几何的定义，p1和p2应满足以下关系：

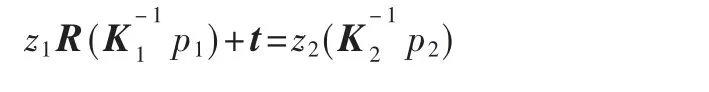
等式两边左乘(K-12p2)^，得：

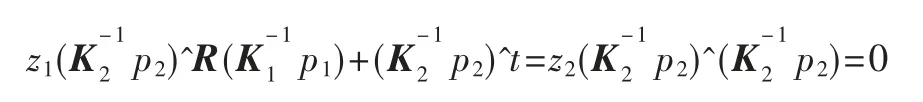
从而可以求出像素深度z1，得到空间点坐标p=。

2 无人机动态目标跟踪模型

无人机动态目标跟踪模型根据目标的位置信息，改变电机的转速，从而控制无人机的位置与姿态，实现对动态目标的平稳跟踪[7]。

为了简化计算，使机体坐标系{B}与左相机坐标系重合(x 轴向右，y 轴向上，z 轴向前)，无人机起飞至高度为1 m 并稳定后，定义此时的机体坐标系为大地坐标系{W}。

在大地坐标系{W}下，定义无人机俯仰角θ，滚转角φ，航向角ψ。在机体坐标系{B}中，设目标的期望位置为p*=(x*，y*，z*)T，实际位置为p=(x，y，z)T。

追踪目标时仅改变无人机在大地坐标系{W}下x、y、z 三轴的位置，不改变航向角ψ。由于无人机在低速状态下，θ ≈0,φ ≈0，故认为{B}与{W}仅相差一个平移[8]，从而{W}与{B}之间的位移、速度变换是线性的。为确保追踪过程中机体的稳定，减少振荡，分别设计位置串级PID 控制和姿态串级PID控制。

2.1 位置串级PID 控制

如图7 所示，位置控制由两个闭环组成，选择双目相机作为信号反馈源。外环为位置控制，由反馈的位置p，根据期望位置p*，通过P 控制方法计算控制输入量，并作为速度环的期望速度v*。内环为速度控制，由反馈的无人机相对于目标的速度v，并根据期望速度v*，通过PID 控制方法计算控制输入量，作为期望加速度a*。

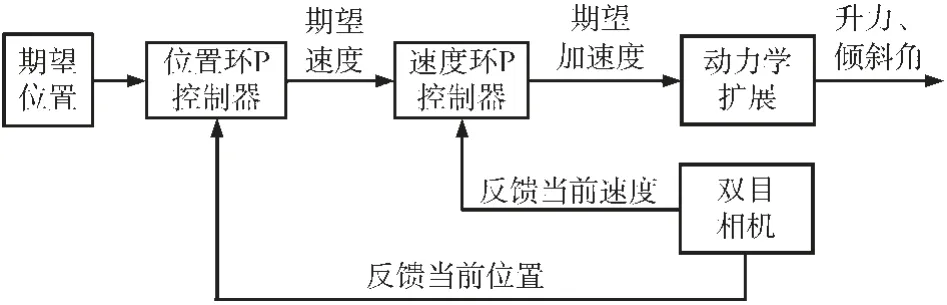
图7 位置控制系统结构图

如图8 所示，通过动力学扩展，又可将期望加速度a*用期望升力、期望姿态角θ*、φ*表示：

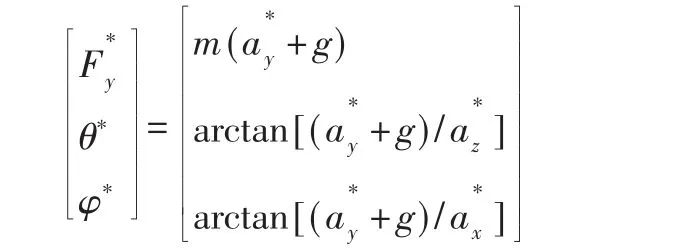
从而，期望的四个电机产生的总拉力为：

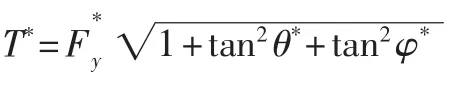
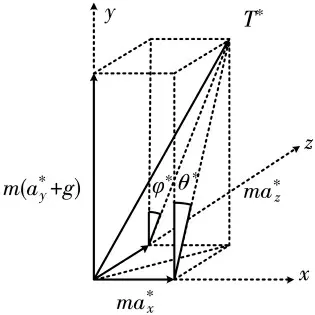
图8 平面受力分析

2.2 姿态串级PID 控制

如图9 所示，姿态控制由两个闭环组成，IMU 作为信号反馈源。外环为角度控制环，由反馈的角度Ψ=(θ，φ)T，根据上一节位置控制推导的期望角度Ψ*，采用P 控制计算控制输入量，作为内环的期望角速度ω*，再由反馈的角速度ω=(ωθ，ωφ)T，采用PID控制计算控制输入量，即期望角加速度。再由动力学，映射到扭矩：

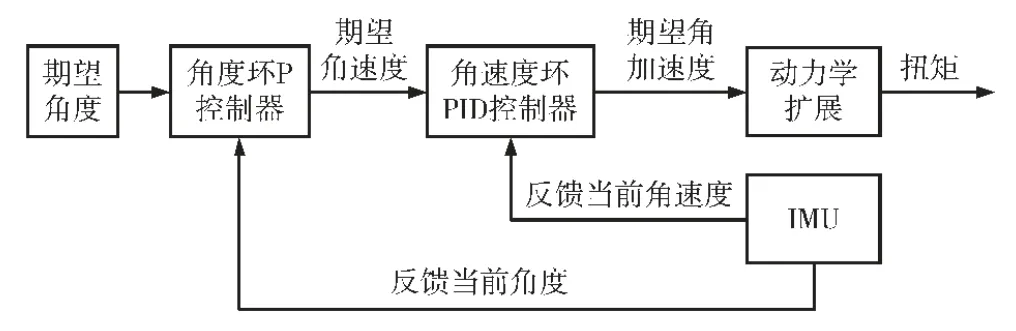
图9 姿态控制系统结构图

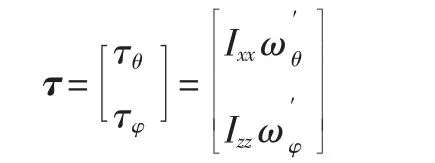
2.3 电机转速控制

本文无人机的电机布局为“X”形，由总拉力T和扭矩τ，便可计算出达到期望状态所需的电机转速：

其中k 为桨叶升力系数，l 为相邻电机间距。给定各控制环合适的PID 系数后，控制模型通过双目相机的位置反馈和IMU 的姿态反馈，实现了由目标位置到电机转速的控制映射：p(t)→ω2(t)。

3 实验与结果分析

3.1 整体框架

四旋翼实验平台(见图10)的目标跟踪系统包括硬件与软件两部分。硬件部分由双目相机、微型视觉计算机和飞控组成。

图10 四旋翼实验平台

双目相机获取视频信息并传输到微型计算机中，计算机在视频中逐帧识别提取出目标，将目标的图像坐标解算为机体坐标系下的空间坐标，同时将坐标信息发送到飞控。飞控接收计算机的目标位置反馈，运行四旋翼目标追踪控制算法，通过调节各电机的转速，控制机体追踪目标。

双目相机选择全瑞视讯高清双目相机(图11)，60 fps，双目分辨率为2 560×960，视角为70°。微型计算机选择Nvidia TX2，飞控选择基于STM32 芯片的开源飞控Pixhawk 4。

图11 双目相机

3.2 相机标定结果与验证

3.2.1 双目标定实验

以一张8×6 棋盘格(图12)作为标定物，分别对左右单目进行标定，定标板每个棋盘格大小为60 mm×60 mm，试验分别选取了18 幅不同距离与角度下的有效图像。

图12 标定棋盘格

标定结果如下，

内参：

畸变系数：

根据多对左右图像的棋盘格角点计算单应矩阵H，进而得到R、t。

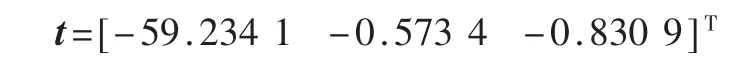
标定结果显示左右两个相机投影面基本平行，平移量t 大致符合59.5 mm 的测量数据。再次对一张双目图像(图13)提取匹配特征点p1，i和p2，i，验证对极约束：

图13 特征匹配

理想情况下e=0，验证结果如表1 所示。

表1 对极约束误差

由表1 中数据，误差e 基本接近0，标定结果符合对极约束的精度要求。

3.2.2 双目测距实验

由双目图像检测出的圆心像素坐标puv1，puv2，从而计算出目标在左相机坐标系下的位置。

图14 为双目相机拍摄的不同距离不同角度下的目标图片(仅显示左图)，解算的目标位置信息和距离与实际测量距离以及误差如表2 所示，发现误差不超过100 mm。

图14 不同角度距离下的目标位置

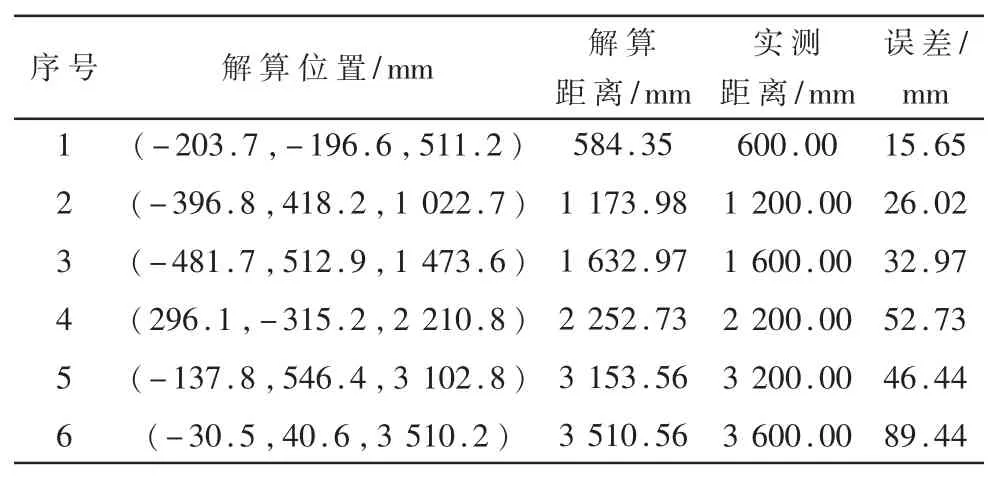
表2 目标解算位置与实测位置对比

3.3 目标跟踪实验

为了提高追踪的准确性和有效性，所选择的追踪目标为椭圆物体。设定目标的期望位置为p*=[0，0，2 000]T，在实验中，空中目标以约300 mm/s 的速度做定速无规则运动，四旋翼无人机需要对空中的物体进行锁定以及实时追踪，具体流程见图15。

图16 是对静止空中目标的追踪实验截图。选取了追踪具有代表性的12 帧左相机的图像，展示了无人机悬停→追踪→预定位置悬停的状态过渡。对静止目标的追踪效果良好，但是存在一定程度的超调，因为设置PID 参数时假定了目标是定速运动。

图17 是对动态空中目标的追踪实验截图，选取具有代表性的12 帧左相机的图像，展示了无人机悬停→追踪→相对静止的状态过渡。对于运动方向变化平缓的目标，无人机可以实现较稳定的跟踪，而如果目标的方向发生大的变动，则无人机在追踪过程中会可能在期望位置来回摇摆，尤其是目标速度在左右方向变动时，甚至可能会跟踪丢失。

图16 目标追踪(静止目标)

图17 目标追踪(动态目标)

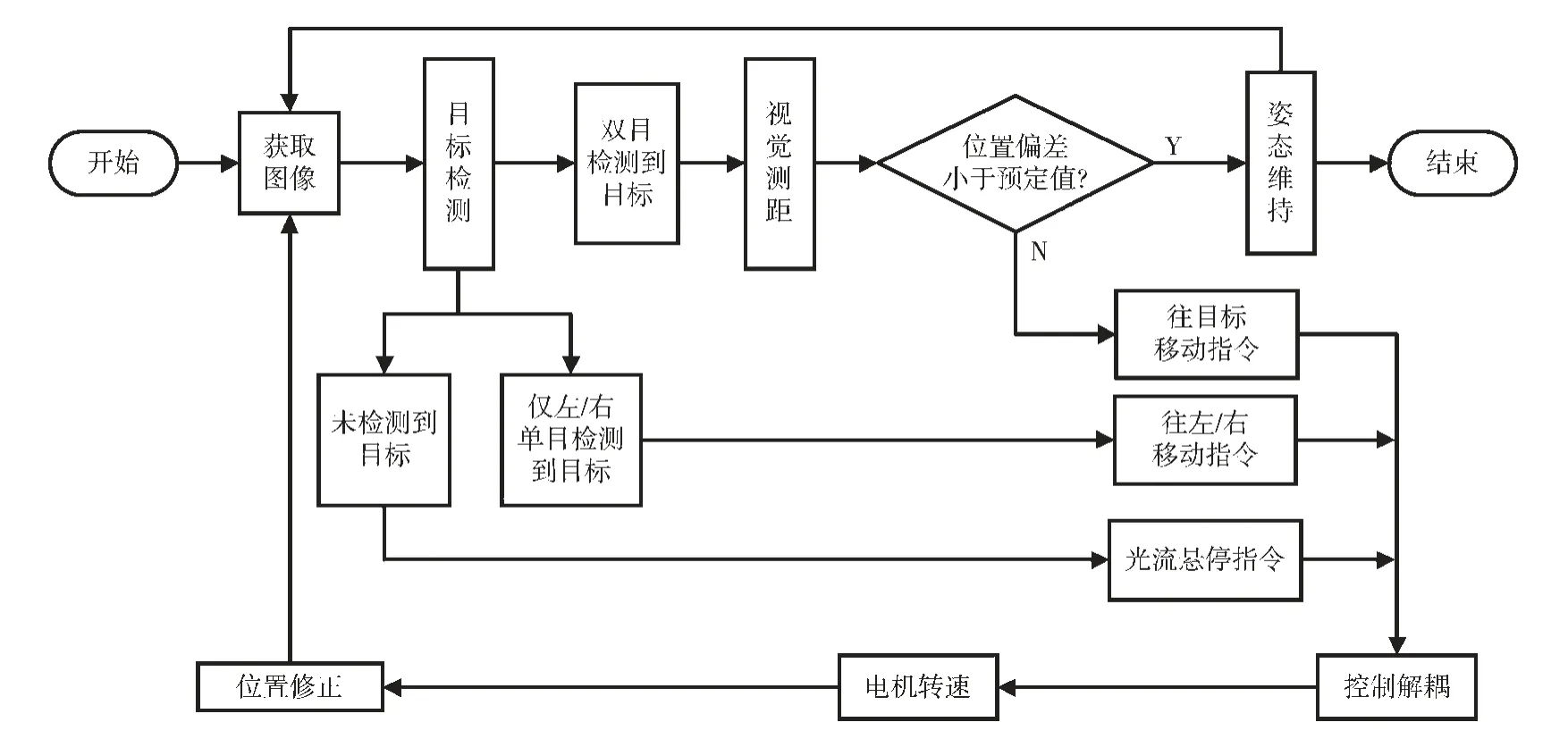
图15 视觉追踪总流程

4 结论

本文将双目视觉测距和目标追踪相结合，利用改进的椭圆检测算法以及三角测量原理，利用目标的有限信息实现了对无人机位姿和目标位置速度的有效估计，针对运动目标跟踪任务，设计并实现了基于串级PID 的四旋翼位姿控制率。将图像处理算法与四旋翼控制相结合，进行了测试实验，验证了本文所提出的目标追踪飞行控制方法。

当无人机与目标横向相对速度小于1.2 m/s，距离小于4 m 时，跟踪效果良好，如在该方案基础上进行相应改动可以实现避障与导航，这对小型无人机在复杂室外环境的应用具有很大的意义。