对称电磁轴承刚性转子系统的动力学特性
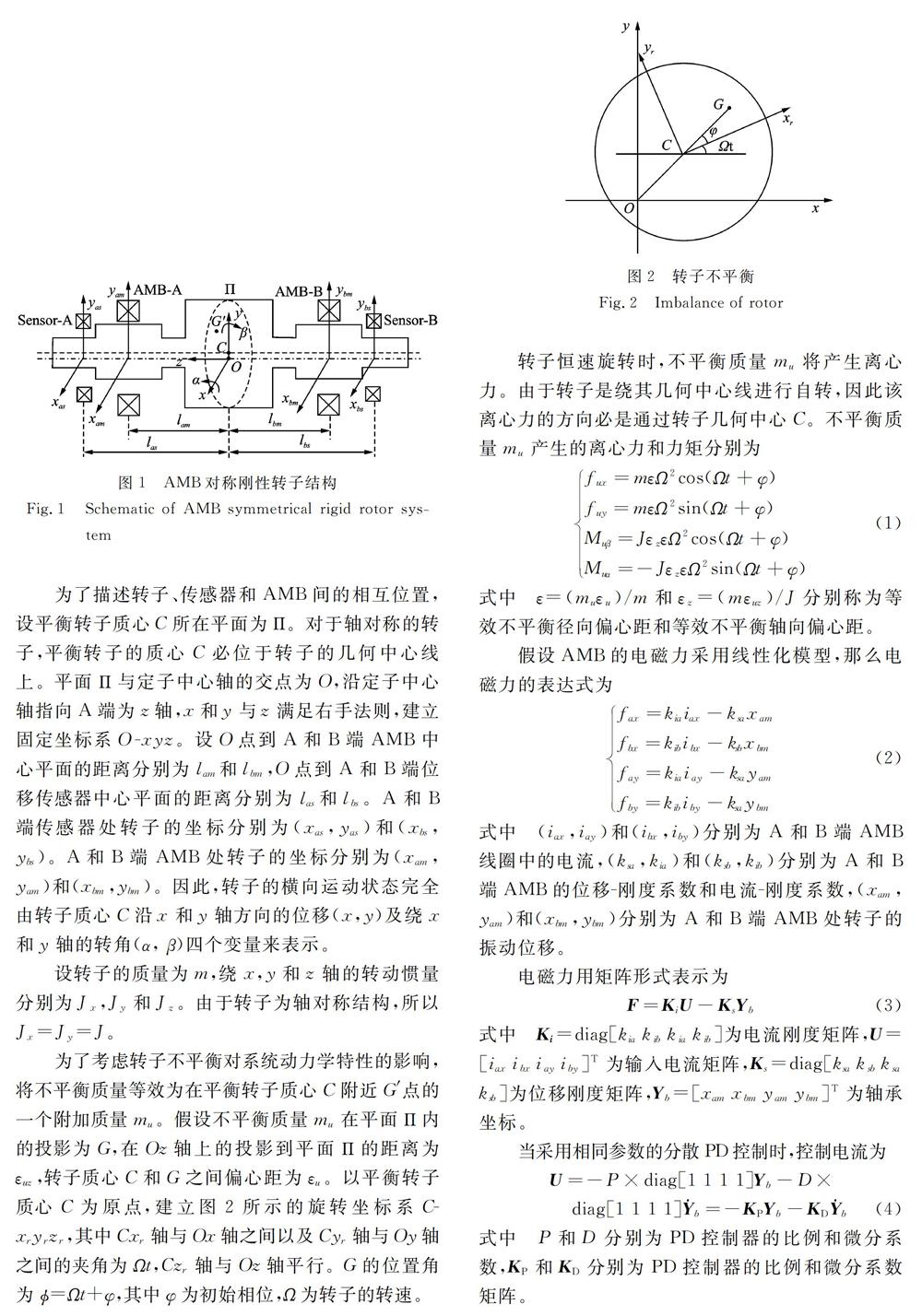
2020-12-18赵皓宇祝长生
赵皓宇 祝长生


摘要:为了研究带有比例微分控制的对称电磁轴承刚性转子系统的动力学特性,首先建立了对称电磁轴承刚性转子径向四自由度系统的动力学模型,并将转子系统的运动分解为平动运动和锥动运动;其次,分别求解平动运动及锥动运行的特征根,利用特征根分析了比例系数、微分系数以及转子转速等参数对平动运动和锥动运动固有特性的影响,并提出了比例微分控制器参数的设计原则;然后,求得了由转子不平衡引起的平动和锥动振动的解析表达式,分析了转子刚体平动及锥动的共振特性以及控制器参数对转子系统不平衡振动的影响;最后,通过实验,对对称电磁轴承刚性转子系统动力特性的理论分析结果进行了验证。
关键词:转子动力学;电磁轴承;刚性转子;比例微分(PD)控制;转子不平衡
中图分类号:0347.6文献标志码:A 文章编号:1004-4523(2020)05-0940-12
DOI:10.16385/j.cnki.issn.i004-4523.2020.05.009
引言
电磁轴承(也称之为主动电磁轴承ActiveMagnetic Bearing,以下简写为AMB)通过对电磁铁线圈中电流的实时控制,使其产生受控的电磁力来实现对转子的悬浮,具有无接触、适合高速、动力特性易于控制等特点,已成为高速旋转机械的典型支撑单元。为使AMB支承的转子系统具有良好的振动特性,过去虽然已经提出了一系列的智能控制方法,如鲁棒控制、自适应控制、非线性控制等,但工程中最常用的仍然是分散的比例一积分一微分(PID)控制。大量的实践已经证明,分散控制在大量AMB转子系统中的控制性能和鲁棒性都能够满足一般的工程要求。
就分散PID控制的AMB支承的刚性转子系统而言,其动力学特性的分析通常有根轨迹法、频率特性法、相位图法和时域仿真法等。由于系统特征根能够准确地描述系统的频率和衰减等特性,因此刚性转子系统稳定性分析首选特征根法。Polajzer等用根轨迹法设计了一种PI和PD级联的位置控制器,研究了控制器的稳定性。Fan等利用根轨迹法研究了陀螺效应对AMB转子系统稳定性的影响。Psonis等利用特征方程和劳斯稳定判据研究了单自由度AMB转子PD闭环系统的稳定性。Yang等给出了单自由度AMB转子PD闭环系统特征根的解析式,分析了PD控制器的整定问题。肖凯等分析了单自由度AMB转子系统的动态刚度和阻尼特性以及PD控制器参数对其刚度和阻尼特性的影響。Akash等在研究单自由度模型的基础上,引入自适应PID技术,对系统进行闭环控制。董淑成等用根轨迹法分析了PD参数对AMB刚性转子系统特性的影响,然后结合相位图法对积分参数的作用进行了分析。雷新亮等根据单自由度AMB系统模型求得了PD参数的稳定域,分析了控制器参数对转子动力特性的影响,最后用实验对控制参数进行修正。袁崇军等以多质点离散转子为对象,采用迭代算法逼近系统特征根,用迭代计算结果判别AMB转子系统的稳定性。汪希平根据单自由度AMB转子系统的传递函数,计算了系统复刚度和复阻尼,分析了系统的阻尼和共振频率特性。wei等在分散PID控制器中加入滤波器,以改善系统的动态特性。Kascak等研究了PD控制下AMB转子系统的稳定性问题。
本文首先建立了考虑转子不平衡的对称AMB刚性转子径向四自由度系统的动力学模型;其次在分散PD控制下得到了转子各模态特征根的解析表达式,从而获得了转子系统自然振动衰减特性和频率特性;然后求解了转子不平衡响应的解析表达式,分析了转子系统的刚体共振等特性;最后通过实验对相关理论结果进行了验证。
1对称AMB刚性转子系统的动力学模型
如图1所示为一般的AMB轴对称刚性转子系统的结构。
由微分方程理论可知,非齐次微分方程的解分别由非齐次微分方程的特解以及与之对应的齐次微分方程的通解两部分组成。在动力学中,将非齐次微分方程的特解称为系统的受迫振动,其特性由不平衡激振力决定。转子系统齐次微分方程的通解称为系统的自然振动或固有振动,它仅由系统本身的特性决定,与外部激励无关。由此可见,转子系统非齐次微分方程式的特解表示了不平衡引起的转子系统平动/锥动的受迫振动。在没有其他外部激励的情况下,转子系统平动/锥动的受迫振动由转子的不平衡力决定。因此这种受迫振动又称为不平衡振动;而与之对应的齐次微分方程式则表示了系统平动/锥动的固有振动,即系统的固有特性。
下面首先求解齐次微分方程式(15)和(16),以研究转子系统平动/锥动的固有特性。然后求解非齐次微分方程式(13)和(14),以研究转子不平衡量导致的系统受迫振动。
2对称AMB刚性转子系统的固有特性
2.1转子平动振动的固有特性
a)D值不能选得过低。由表2可知,平动和锥动的衰减主要由D决定。如果D选得过小,就无法为系统提供足够阻尼,使振荡迅速衰减,导致系统响应速度慢,当系统中存在非线性时闭环系统甚至会出现不稳定问题。
b)D值不能选得过大。由于速度信号中的噪声要比位移信号中的噪声更为严重,因此,高阻尼系统就意味着高噪声水平,只有保证位移和速度信号中的噪声水平足够低,才能考虑选择较高的阻尼。对于复杂的AMB刚性转子系统来说,位移传感器、功率放大器、外部流体和电气等设备都会引人噪声,因此不宜采用过高阻尼的控制方式。
c)D值的选取应与比例系数P的选取相配合。由表2可知,转子系统的固有频率由系数P和D共同确定,所以为了达到满意的控制效果,二者必须在选择上进行配合。以WFw为例,当提高系数P时,WFw会随之增大,此时若再减小系数D,则WFw会变得更大,严重时甚至可能超过系统带宽,造成系统失稳。由此可见,P值越高,D值必须选择越大,以保证频率在一个合理的范围内。
4解析分析和实验结果
解析分析和实验中AMB对称刚性转子系统的相关参数如表1所示。根据表1中系统参数,由式(37)和(38)计算出比例系数P和微分系数D的数值。取k=2,v=0.2时,P=6335,D=3.5。
根据解析式计算得到转子系统的振动响应曲线如图13所示。
图14为某磁悬浮高速电机实验装置,该实验平台由电源,变频器,dSPACE,传感器,开关功放,电机和上位机等组成。电机的转子径向由两个AMB支撑,轴向由一对永磁轴承支撑。
在P=6400,D=5的条件下,实验得到的转子系统振动响应曲线如图15所示。实验结果表明,根据转子系统固有振动特性所选择的PD参数能够使实际转子系统稳定运行,并具有较好的动态特性。将图13与15进行比较可知,解析式能较为准确地反映AMB刚性转子系统的运动状态。
理论解析与试验结果之问存在一定差异的主要原因为:
1)实际系统任一时刻的运动都是由固有振动和不平衡振动共同组成。转子在0转速附近时,不平衡振动很小,固有振动对转子振动幅值的影响尤为明显。然而实验中固有振动幅值由初始条件决定,具有随机性,因此解析式曲线与实验曲线在0转速附近区别较为明显。
2)实际系统并非完全对称系统,主要表现在转子质心并不是准确位于两端电磁轴承的中点处。这种非对称性将平动与锥动耦合在一起,对转子系统的运动特性造成影响。
3)实际控制系统中存在的滞后(如采样滞后,计算滞后等),以及功放传感器等环节的延迟效应,都会影响转子系统的运动特性。
5结论
针对对称AMB刚性转子PD闭环系统的动力特性进行了解析分析,得出如下结论:
(1)对称AMB刚性转子的平动和锥动方程互相解耦,可以分别对转子的平动和锥动振动的固有特性及不平衡响应特性进行解析分析。
(2)对称AMB刚性转子PD闭环系统的固有振动特性不仅与系统的动力学参数有关,而且还与PD控制器的比例系数P和微分系数D有关。当选取P为“自然”刚度时,D值应与P值相匹配,才能够保证闭环系统稳定运行,且具有良好的动态特性。
(3)对于对称AMB刚性转子PD闭环系统,当转速较低时,转子系统的不平衡振动受P和D参数的影响较为明显,调节P和D参数,可以调节平动位移共振和锥动角度共振点的位置和振幅。
