基于三维形貌和剪胀效应的软-硬节理抗剪强度模型
2020-12-18金磊磊魏玉峰
金磊磊,魏玉峰
(地质灾害防治与地质环境保护国家重点实验室(成都理工大学),四川,成都610059)
节理是一种十分常见的地质构造,较为普遍的出现在岩体中,其不连续性极大地影响着岩体的力学性质,对人类的工程建设活动造成了一定程度的困扰[1−2]。岩体节理抗剪强度计算在岩土工程领域起着重要作用,是岩质边坡等稳定性评价的重要依据。
节理的剪切强度特性一直是国内外学者研究的热点。Patton[3]研究了锯齿状人工节理在不同法向应力下的剪切强度,将剪胀效应引入摩尔-库仑准则中建立了双线性强度包络线。此后大量学者以Patton 的理论为基础,用各类参数表征峰值剪胀角在节理剪切过程中的变化规律,从而建立各自的岩石节理抗剪强度模型。Maksimović[4]采用节理粗糙角Δφ和中位角压力值PN表示峰值剪胀角,建立非线性岩石节理抗剪强度模型。肖卫国等[5]基于岩体节理变形的非线性特征,针对剪切过程中节理微凸体的磨损与破碎而导致的应力下降,提出了考虑峰后软化的切向变形的本构模型。尹显俊等[6]研究了岩体结构面循环加载的强度,并建立了本构模型。Kulatilake 等[7]引入固定粗糙度参数SRP和平均倾角I建立岩石节理抗剪强度模型。Barton[8]以大量岩石节理的剪切试验为基础,采用节理粗糙度系数JRC和节理抗压强度系数JCS共同表示剪胀角随法向应力的变化规律,提出了经典的JRC-JCS岩石节理抗剪强度模型。Wei等[9]采用三轴试验对Barton 模型的可靠性以及适用范围进行了论证。


目前关于岩石节理的研究,主要集中于上、下盘抗压强度相同的常规节理,对于上、下盘抗压强度不一致的软-硬节理的研究较为少见。Nasir等[25]研究了矿山回填中胶结填充体(CPB)与围岩的剪切特性。Wu 等[26]以三峡地区的泥岩与泥质灰岩的层面为研究对象,建立了神经网络用以预测软-硬节理的抗剪强度。Ghazvinian 等[27]研究了软硬互层的岩质边坡的层面,以此为基础对Barton 模型进行改进。宋磊博等[28]采用等效节理抗压强度反映软-硬节理在剪切过程中的抗压强度系数,从而对Barton 模型进行修正。
自然界中岩石节理形貌多样复杂,学者的研究长期受困于节理试验的不可重复性,而水泥砂浆浇筑的人工节理解决了这一难题,但受限于技术,以往人工节理的研究多是简单的锯齿状[3,26−27]。随着3D打印技术的成熟以及和光学扫描技术的结合,采用水泥砂浆仿制天然节理形貌的人工节理试样,使相同节理的重复试验成为可能[29]。伴随着科学技术的进步,更多的仪器设备支持着科研工作者的研究,CT 扫描仪以及三维光学扫描仪越来越多的应用于岩土工程领域的研究,打开了岩石节理研究的细观领域。CT扫描技术多用于岩石的细观损伤特性的研究[30],而三维光学扫描技术常用于采集节理面形貌特征等信息。Jiang 等[31]将基于3D打印技术制作的人工节理和天然节理进行对比,证实了3D技术的可靠性。Head 等[32]采用3D打印技术,打印出岩石内部的微观特征,用于研究岩石微观结构变化对渗透率的影响。肖维民等[33]将3D打印技术用于柱状节理的研究。刘泉声等[34]采用Visijet PXL 类石膏作为3D打印的原料,打印出仿真的岩石试样。
本文借助三维激光扫描技术和3D打印技术制作人工节理模具,采用水泥砂浆浇筑与天然节理形貌相同的人工节理试样,其中包括上、下盘抗压强度一致和上、下盘抗压强度不一致的人工节理,在此基础上开展试验研究。为表征节理上、下盘抗压强度不一致的特性,定义了节理强度比[28],如式(1)所示。

对人工节理试样进行常法向应力下的剪切试验。根据试验结果,分析了不同三维形貌以及不同节理强度比对节理剪切强度特性的影响。将试验结果和理论推导结合,建立含有三维形貌参数以及节理强度比适用于软-硬节理的抗剪强度模型。并对所建立模型的适用性及可靠性进行了深入的探讨和研究。
1 人工节理的室内试验
1.1 人工节理试样的制作
常法向应力剪切试验(CNL)一直被认为是测试岩石节理强度特性和变形特性的有效手段。以往的研究受限于自然节理的复杂多样,不能制备相同的节理试样,无法进行同一个节理形貌在多个法向应力下的剪切对比。故而本文选用天然节理的水泥砂浆复制品替代进行试验。
采用三维激光扫描仪对取自某大型深基坑内的节理岩样进行扫描,扫描过程如图1所示。

图1 节理面信息采集Fig.1 Joint surfaceinformation collection
扫描后,提取研究区域的节理面信息,在后处理软件中建立节理的三维实体,将三维实体切片后,导入3D打印机,打印制作人工节理模具。人工节理模具的制作过程如图2所示。
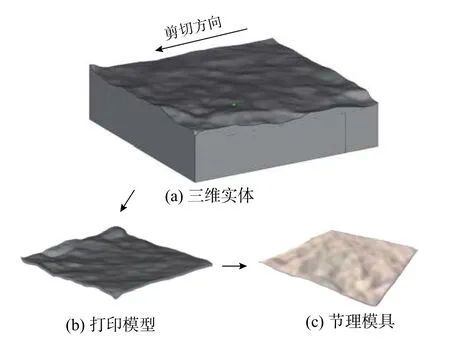
图2 人工节理模具的制作Fig.2 Manufactureof manual joint mold
为提高试验的精确性,在制样过程中严格控制水泥砂浆的配比以及砂和水泥的选料。选用标准砂和早强水泥,经过调试对比确定三种不同强度(高、中、低)的水泥砂浆,用于浇筑不同抗压强度的节理盘,不同配合比水泥砂浆的基本参数见表1。

表1 不同配比水泥砂浆的基本参数Table 1 Basic parameters of cement mortar with different proportions
根据以往的试验经验,砂浆在浇筑振捣和凝固的过程中,内部气体多由上表面溢出。若将人工节理模具置于上部,采取压模的形式制作人工节理,极易出现蜂窝麻面等情况,对节理试样表面的抗压强度产生较大的影响。故而浇筑人工节理时,将人工节理模具水平放置于浇筑盒底部并固定,防止浇筑时发生偏移。而后在浇筑盒内壁均匀的涂上液体脱模剂,将水泥砂浆分层加料至浇筑盒内,置于振动台上,高频轻振,充分振捣,排出砂浆内部气体,当浇筑至浇筑盒顶部后,将其抹平。人工节理的浇筑过程如图3所示。

图3 人工节理的浇筑Fig.3 Artificial joint casting
按照上述人工节理的制作流程,采用低强度水泥砂浆浇筑3种不同粗糙度的人工节理。3组人工节理分别记为K-I、K-II、K-III,每组5个试样。用于做相同节理强度比、不同粗糙度条件下节理剪切试验的对比分析。
对于节理模型K-III组,再浇筑两组不同强度比的人工节理试样。分别为:中强度水泥砂浆浇筑下盘,低强度水泥砂浆浇筑上盘的K-III-2组;以及高强度水泥砂浆浇筑下盘,低强度水泥砂浆浇筑上盘的K-III-3组,每组5个试样。K-III、K-III-2、K-III-3三组人工节理试样用于做相同粗糙度、不同节理强度比条件下节理剪切试验的对比分析。各组人工节理的水泥砂浆使用情况见表2。
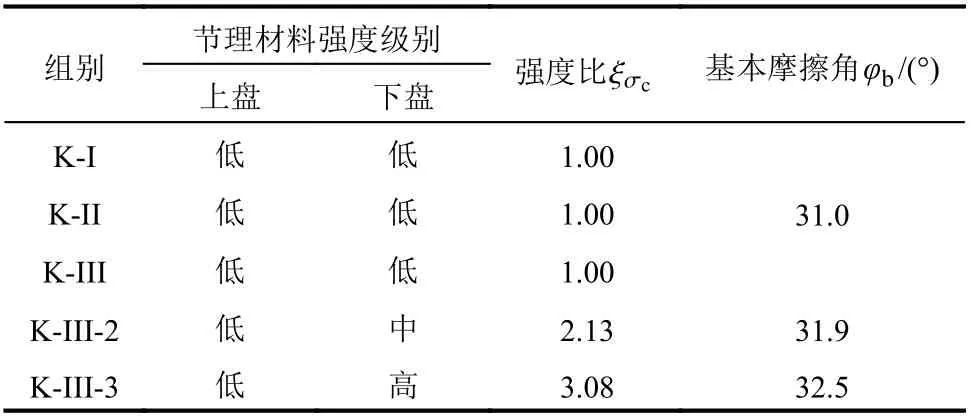
表2 人工节理的基本参数Table 2 Basic parametersof artificial joints
采用成都理工大学地质灾害防治与地质环境保护国家重点实验室的岩体剪切试验仪,对养护好的人工节理试件进行常法向应力下的剪切试验。每组试样共进行五级法向应力下的剪切,五级法向应力分别为0.5 MPa、1.0 MPa、1.5 MPa、2.0 MPa、3.0 MPa。试验开始时采用应力控制法,施加法向应力达到预定荷载后,采用位移控制法,施加剪切应力直至试验结束。剪切加载速率始终保持为1.0 mm/min,设定剪切位移为15 mm,保证出现残余抗剪强度或试样破坏不能继续剪切。
1.2 节理面的三维量化
Hopkins[35]认为,对于承受法向应力的岩石节理,总接触面积通常远小于节理表面的70%。Grasselli等[17−19]观察剪切后的节理面变化特征,证实在真实的节理剪切过程中,实际接触面积仅占节理表面的一部分,且接触部分的分布具有明显的随机性,很难通过节理粗糙系数JRC这样的二维剖面来表征。本文采用三维激光扫描仪对人工节理试样进行扫描,提取高程信息,采样间距为0.3 mm。
Grasselli 将节理面扫描后离散化,以每个小三角形作为一个微单元。如图4所示,方位角 α是节理微单元倾角向量d在剪切平面ω上的投影与剪切向量t的夹角。倾角θ是剪切面与节理微单元的夹角。节理的接触取决于节理微单元沿剪切方向上的视倾角 θ∗的大小。视倾角计算式(2)。所有节理微单元中沿剪切方向上视倾角最大的角度,称为最大视倾角θm∗ax。

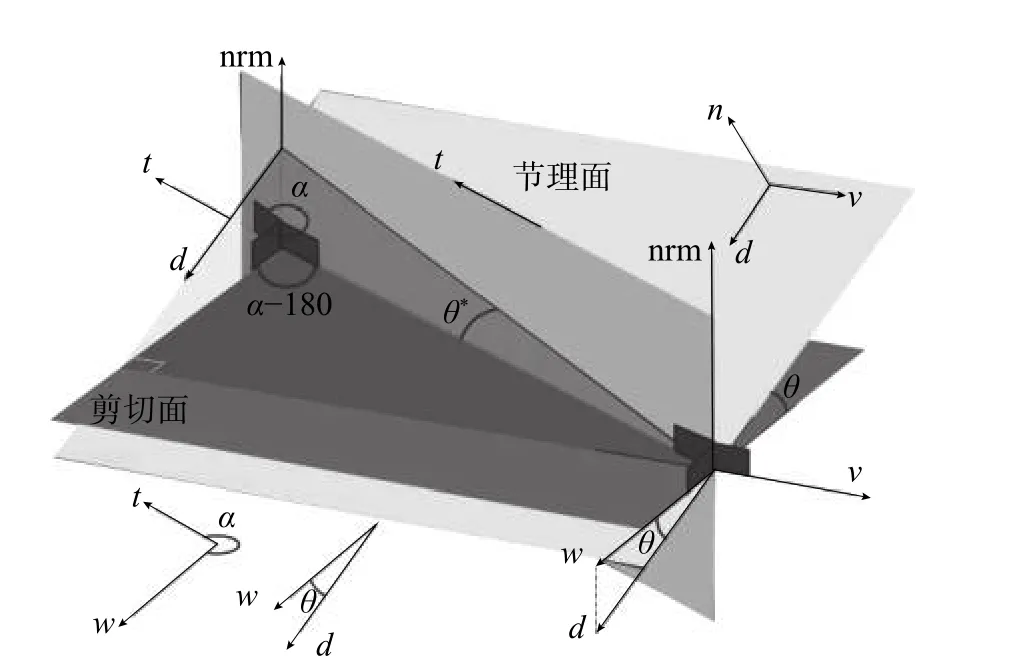
图4 节理表面形貌三维量化[17 − 19]Fig.4 3D quantification of joint surface morphology[17− 19]
节理剪切时,潜在磨损(碎)区仅发生在面向剪切方向上较陡部分的微单元。因此只有微单元的倾角较大时,才能对节理剪切的力学行为产生直接影响。剪切时不同法向应力和不同剪切方向均存在一个临界视倾角 θ∗cr。临界视倾角 θc∗r的取值范围在0到最大视倾角θ∗max之间。当节理微单元视倾角大于临界视倾角时θ∗≥θc∗r,为节理面的潜在接触区域;当节理微单元视倾角小于临界视倾角时θ∗<θc∗r,为非接触区域。潜在接触区域的面积

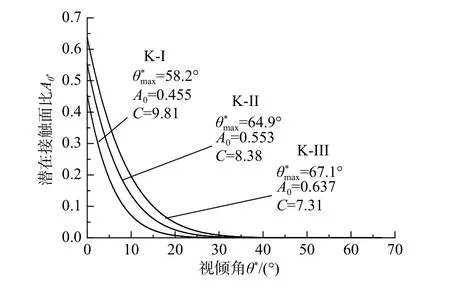
图5 潜在接触面比 Aθ∗ 与 θ∗视倾角的关系Fig.5 Relationship between potential contact surface and apparent inclination angle
各组人工节理试样的形貌参数如图5所示。粗糙度参数C表示节理的粗糙程度,C值越小节理面越粗糙。理论上,粗糙度参数C的取值范围可由0到+∞,当C等于0时,节理面为锯齿状,所有节理微单元都具有相同倾角;当C趋于∞时,表示节理是一个光滑的平面。由节理三维形貌参数可知,3组人工节理的粗糙程度按K-III、K-II、K-I依次递减。
对于新鲜的张拉节理或者完全吻合的人工节理,虽然上、下盘的扫描面有所不同,但无论扫描节理的上盘或是下盘,将节理面离散化后,其对应位置的微单元视倾角是相同的。在剪切方向固定的情况下,潜在接触面积比的计算值不会因为节理的上、下盘而改变。故而对于同一个节理的上、下盘,三维形貌参数是一致的。
2 软-硬节理抗剪强度模型的建立
2.1 节理剪切的强度特性及变形特性分析

图6 K-I 组节理剪切应力-位移曲线Fig.6 Shear stress-displacement curve of K-I joint

图7 不同强度比节理剪切应力-位移曲线( σn=1.50 MPa)Fig.7 Shear stress-displacement curvesof joints with different strength ratios
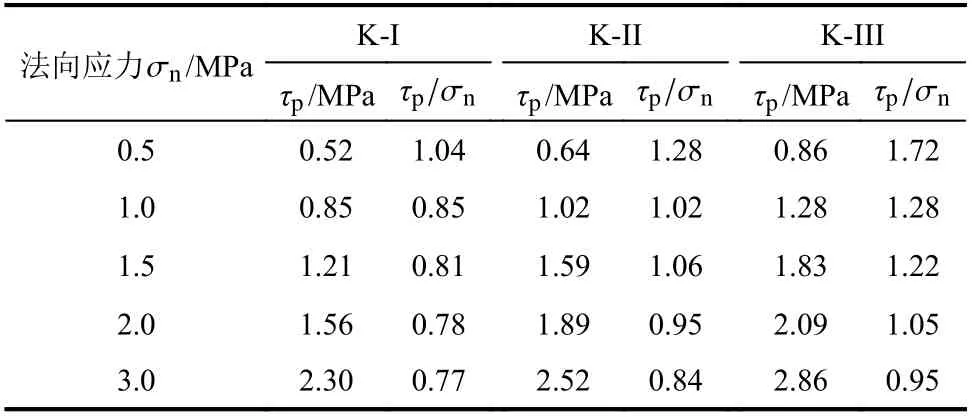
表3 不同粗糙度节理直剪试验结果Table 3 Direct shear test resultsof jointswith different extents of roughness

表4 不同强度比节理直剪试验结果Table 4 Direct shear test resultsof jointswith different strength ratios
图6、图7为节理剪切的应力-位移曲线;表3、表4为节理剪切的峰值抗剪强度,由图、表可知:1)图6中,法向应力为0.5 MPa 时,试样剪切的前1 mm 的位移中,应力没有明显增长,是因为试样与剪切盒未完全贴合存在1 mm 左右的空隙,当施加位移超过1 mm 后,应力才出现增长;2)在节理剪切初期,剪应力随着剪切位移的增长而快速的增长,剪切刚度近似常量,随着剪切的进行,剪切刚度下降,剪应力在达到峰值后趋于稳定;3)节理强度比不变时,随着法向应力的增大,节理的初始剪切刚度、峰值抗剪强度、残余抗剪强度都随之增大。且抗剪强度和法向应力的比值(τp/σn)呈非线性下降;4)法向应力不变时,随着节理强度比的增大,节理的初始剪切刚度、峰值抗剪强度、残余抗剪强度都随之增大;5)节理抗剪强度受节理表面三维形貌特征影响,相同法向应力作用下粗糙度越大,节理的抗剪强度越大。
2.2 软-硬节理抗剪强度模型的建立
节理峰值抗剪强度在低法向应力下满足摩尔-库仑强度准则[3],其形式为:

图8为直剪试验的峰值剪胀角与法向应力的关系,由图可知:对于三维形貌相同的节理,法向应力越大,剪胀角越小;法向应力相同时,节理面越粗糙,剪胀角越大。
表5为不同法向应力作用下各人工节理试样对应的峰值剪胀角。采用Boltzmann 函数对各组节理在不同法向应力下的峰值剪胀角进行分析,进而得出初始剪胀角。Boltzmann 函数的表达式为:

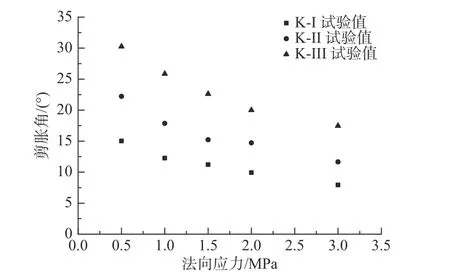
图8 节理剪胀角与法向应力的关系Fig.8 Relationship between dilation angle and normal stress

表5 各组人工节理的峰值剪胀角Table 5 Peak dilatancy angle of artificial jointsin each group


3 软-硬节理抗剪强度模型与Barton模型的比较分析
Barton[8]提出的JRC-JCS抗剪强度模型,是目前在岩石工程领域中应用最为广泛的节理抗剪强度估算准则。

Barton 和Choubey[10]基于对大量岩石节理的剪切试验,绘制出10条标准粗糙度剖面线用以参照评估JRC的值,其取值范围为0~20。但是该方法的肉眼评估存在人为主观因素,易造成偏差。
为提高Barton 模型计算的准确性,本文采用Tse等[11]提出的一阶导数均方根Z2式(14),以及建立的Z2与JRC的函数关系式(15)来量化节理剖面线的形态,从而计算节理剖面的粗糙度。

式中:L为节理轮廓线的长度;y为节理轮廓线的起伏度。
离散化后的一阶导数均方根Z2如式(16)所示。图9为节理粗糙度计算示意图。

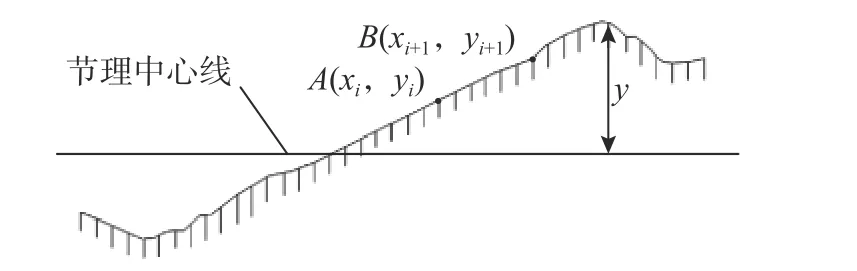
图9 粗糙度计算示意图Fig.9 Roughnesscalculation diagram
节理面抗压强度系数控制着岩体的变形特性和整体稳定,是岩石节理最基本的物理参数。本文采用HT225型回弹仪测量节理面抗压强度系数,按式(17)计算。各组人工节理参数取值见表6。


表6 Barton 模型内各参数Table 6 Parameters in Barton model
图10为本文模型计算值和Barton 模型计算值以及试验值的比较,由图可知:本文模型和节理剪切试验值具有较好的相关性。若采用节理较软盘的抗压强度系数JCScs对Barton 模型进行计算,其结果偏小;若采用节理较硬盘的抗压强度系数JCSch对Barton 模型进行计算,则计算结果远大于试验值,且平均偏差随着法向应力的增大而不断增大。节理抗剪强度试验值更接近由较软盘抗压强度系数JCScs计算的Barton 模型,由此可知剪切过程中节理较软盘抗压强度对节理的剪切强度起控制作用。

图10 K-III-3组本文模型和试验值的比较Fig.10 Comparison of new model and experimental valuesin K-III-3 group


表7 本文模型和Barton 模型的平均偏差/(%)Table 7 Averagedeviation of new model and Barton model
Barton 模型计算常规的岩石节理抗剪强度具有一定的可靠性[9],但对于节理上、下盘抗压强度不一致的软-硬节理不具普遍适用性。由表7本文模型和Barton 模型的平均偏差可知:当节理上、下盘抗压强度相同,即节理强度比 ξσc为1时,本文模型和Barton 模型计算结果的准确度均较高,平均偏差都在10%以内,但本文模型的平均偏差略小。当节理上、下盘抗压强度不同,即节理强度比 ξσc大于1时,Barton 模型采用较软盘抗压强度进行计算时,平均偏差在10%左右;若采用较硬盘抗压强度进行计算时,平均偏差在10%以上;而本文模型的平均偏差在5%以内。由此证明了Barton 模型不适用于软-硬节理的抗剪强度计算,而本文模型对此有较好的可靠性。
4 软-硬节理抗剪强度模型的适用性验证
云南某水电站库区内斜坡的后缘出现了深度达10 m 的拉裂缝。为揭示该斜坡的失稳机理,以及评估斜坡的安全性系数,某勘测设计研究院在山体打入2个平硐。在一号平硐90 m~95 m 洞段内,发现了上、下盘抗压强度不一致的软-硬节理,如图11所示。节理的上盘为长期受高地应力挤压的泥岩,下盘为裂隙较发育的灰岩。考虑到节理的上、下盘抗压强度有较大差别,采用本文提出的软-硬节理抗剪强度模型对该节理的抗剪强度进行计算。

图11 取样点Fig.11 Sampling points
取样时尽量减少扰动,将现场取回的大块、不规则岩样在室内进行切割处理,试样大小控制在10 cm×10 cm 左右。将切割好的试样,采用高强水泥砂浆,固定在剪切盒内,制样过程如图12所示。制备完成的试样如图13所示。将剩余的岩样制成各类试样,用以测试节理岩样的各项力学参数,节理试样各项参数的平均值见表8。
采用岩体剪切仪,对养护好的节理试样进行常法向应力下的剪切试验。在试验前通过三维激光扫描仪获取节理面高程信息,计算三维形貌参数,试验结果以及各参数见表9。

图12 试样的制备Fig.12 Preparation of sample
通过式(18)对本文模型计算值和试验值的平均偏差进行计算,得到的平均偏差为5.54%。由此可知,本文模型的计算值和试验值较为吻合,证明本文模型能够适用于计算上、下盘抗压强度不一致的软-硬节理的抗剪强度。

图13 试成品样Fig.13 Sample

表8 节理材料的基本参数Table 8 Basic parameters of joint materials
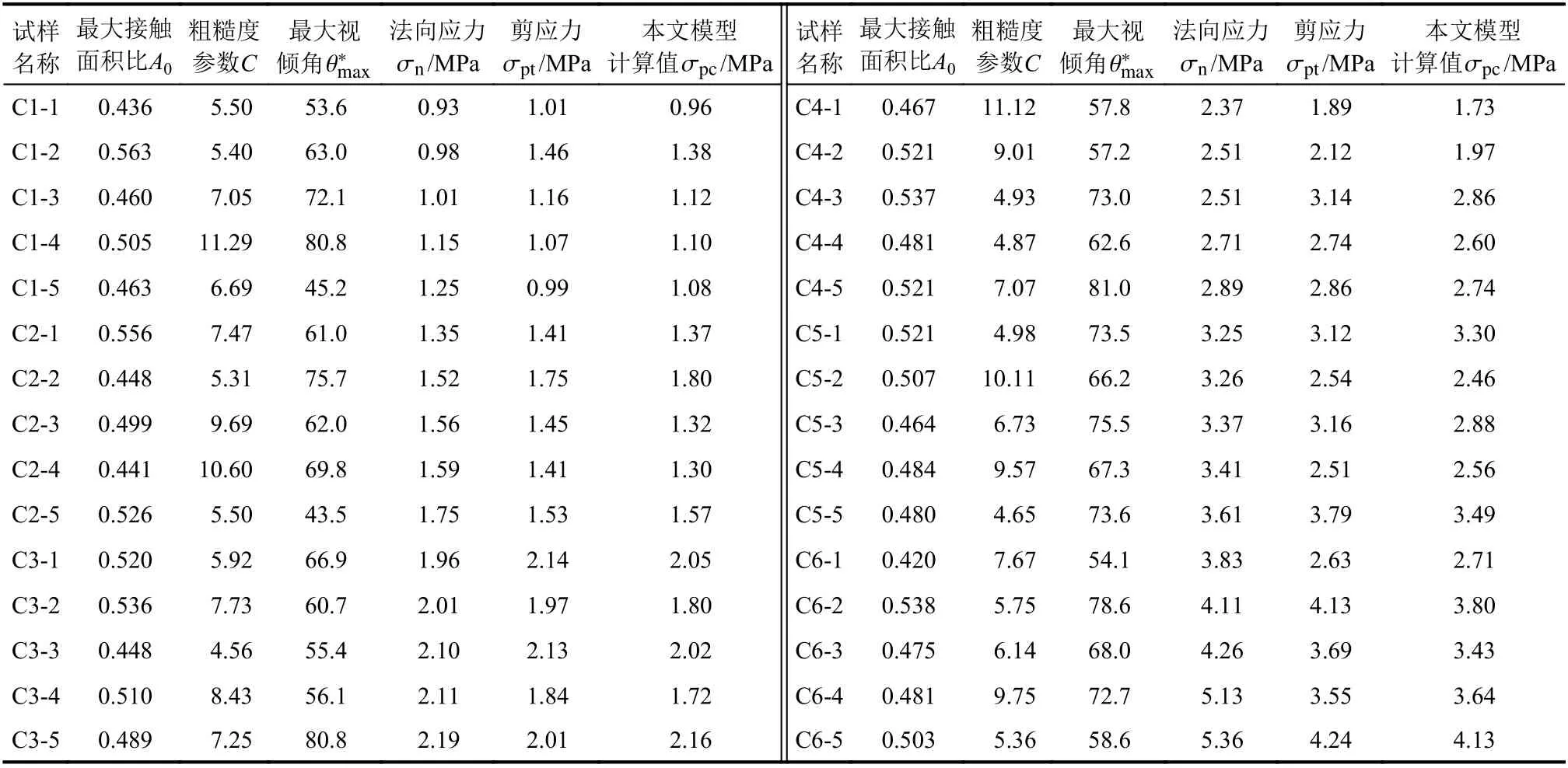
表9 节理表面三维参数及试验结果Table 9 Three-dimensional parametersand experimental results of surface
5 结论
本文借助三维激光扫描技术和3D打印技术,浇筑了具有自然节理形貌的上下盘抗压强度相同和上下盘抗压强度不同的人工节理试样,并对其进行常法向应力下的剪切试验。以剪胀角和三维形貌参数为基础建立岩石节理抗剪强度模型,通过与Barton 模型对比并结合工程实例的应用,得到以下主要结论:
(1)人工节理的剪切试验表明,节理的抗剪强度随节理粗糙度、法向应力及节理强度比的增大而增大;节理的剪胀角随法向应力的增大而减

