KiC：一种结合“结构洞”约束值与K壳分解的社交网络关键节点识别算法

李钢 王聿达 崔蓉

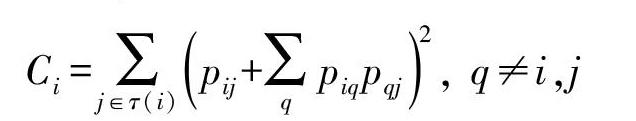
收稿日期：2020-03-19

基金项目：2019年国家社会科学基金项目“智能时代的意识形态风险防范研究”（项目编号：19BKS098）。

作者简介：李钢（1968-），男，教授，博士，研究方向：网络社会管理、网络与公共信息管理。崔蓉（1989-），女，博士研究生，研究方向：复杂网络理论与应用。

通讯作者：王聿达（1989-），男，博士研究生，研究方向：复杂网络与信息传播、数据挖掘。

摘  要：[目的/意义]在大规模社交网络中快速搜索关键节点对于舆情的引导和控制具有重要意义。[方法/过程]本文提出一种适用于社交网络的局部中心性关键节点识别算法，该方法综合评估了节点的K壳、自身的聚集特性以及邻居的扩散特性和节点自身传播状态，同时体现了节点在空间上的网络位置和邻居的拓扑结构以及在时间上演化特征，评价指标更加全面高效。[结果/结论]实验结果表明，该方法识别的关键节点对网络鲁棒性的影响与介数中心性接近，但计算仅基于节点局部信息，时间复杂度低。剔除这些节点后网络的连通性受到较大影响，网络聚类系数降低，平均路径长度增加。同时，利用SIR传播模型模拟验证，以该算法识别的关键节点为初始传播源可提升信息传播范围和平均传播速度。

关键词：复杂网络;关键节点;K壳;约束系数;舆情传播

DOI：10.3969/j.issn.1008-0821.2020.12.003

〔中图分类号〕G201  〔文献标识码〕A  〔文章编号〕1008-0821（2020）12-0027-09

KiC：An Extended K-shell Decomposition Based on

Improved Network Constraint Coefficient

Li Gang  Wang Yuda*  Cui Rong

（School of Economics and Management，Beijing University of Posts and Telecommunications，

Beijing 100876，China）

Abstract：[Purpose/Significance]Evaluating vital nodes rapidly in large-scale social networks is of great significance for the control of information dissemination.[Method/Process]In this paper，we proposed a local centrality vital node identification algorithm.The method comprehensively evaluated the K-shell of a node，its own clustering characteristics，the diffusion characteristics of its neighbors and propagation state of nodes，which simultaneously reflected the network location of the nodes，the topology of the neighbors and evolutionary features in time.The evaluation indicators were more comprehensive and efficient.[Result/Conclusion]The experimental results showed that the vital nodes identified by this method had a greater impact on the robustness of the network.After removing these nodes，the connectivity of the network was greatly affected，the network clustering coefficient was reduced，and the average path length was increased.Meanwhile，SIR model was used to evaluate the ability to spread nodes.Simulations of five real networks showed that our proposed method could improve the scope and average speed of information dissemination.

Key words：complex network;vital node;K-shell;constraint coefficient;information dissemination

近年来，对复杂网络的研究已成为许多领域关注的热点。几乎所有的复杂系统都可以表示为网络，网络的顶点代表实体，而边则表示实体间的关系与相互作用。网络中存在对提高系统鲁棒性意义重大的节点，这些节点一般数量非常少，但其影响却可以快速波及网络中大部分节点。例如：在社交网络中，对少量最重要节点的删除能够有效控制信息的传播。可见重要节点对网络的动力学行为有着巨大的影响。因此，在大规模社交网络中快速搜索关键节点意义重大。

識别网络中的关键节点受到物理、数学、计算机和管理科学等多学科的广泛关注，使其成为各个学科所共同关注的交叉科学，各学科研究人员根据所关注的具体问题，提出了众多重要节点排序方法。利用节点度中心性来判断节点的重要性是最简单的方法[1]，该方法认为，一个节点的度越大，影响力就越大，其缺点是没有全局角度考虑节点所处的网络位置和邻居的拓扑结构，在很多情况下不够精确。介数中心性[2]和接近度中心性[3]从全局出发，分别考虑节点到达其余节点的最短路径数目，节点与其他所有节点最短距离的平均值，此类方法在评估节点重要性方面有了明显的效果，但由于需要获得整个网络的拓扑特征，导致时间复杂度高，不适用于当前社交网络关键节点的识别。为平衡识别效果和时间复杂度，Chen D等[4]提出了半局部中心性，半局部中心性使用了节点的四阶邻居的度作为判断依据，相较介数中心性该算法消耗非常少的计算时间，然而该算法只考虑了邻居节点信息，忽略了节点在全局网络中所处的位置。Burt R S等[5-7]基于经典社会学中的“结构洞”理论，用网络约束系数来衡量节点形成结构洞时所受到的约束，该方法利用了局部属性评价节点的重要性，具有较好的时间复杂度和计算精度，然而，该方案没有考虑邻居节点与其余节点相连的拓扑结构对节点的影响。

Kitsak M等[8]依据网络中节点处于网络的核心位置往往有较高影响力的思想，提出用K壳分解法确定网络中节点的位置，在分析大规模网络的关键节点等方面具有良好的时间复杂度。然而此方法也有一定局限性，如未考虑删除节点等。Zeng A等[9]提出了混合度分解算法，混合度以网络中剩下的邻居节点以及删除的邻居节点的混合度进行K壳计算，此方法较好地提高了节点区分度。王环等[10]提出了点权分解算法，该算法综合考虑了节点的全局指标加权核值以及节点的局部指标度数，真实网络的实验结果表明，此算法在关键节点识别中可取得较好的效果。

综上所述，要准确识别社交网络环境下节点的传播能力，不但要考虑节点所处的网络位置和邻居的拓扑结构，还需考虑计算的时间复杂度，同时由于网络舆情时间特性明显，节点时序特性也是识别关键节点的重要因素。K壳分解算法可以高效准确地识别节点在网络中的位置，然而当前的K壳分解及其优化算法还存在如下局限性：第一，没有考虑邻居之间的拓扑关系，不能在计算中反映邻居节点间的相互作用。第二，缺乏“桥”节点的识别，在社交网络中存在着一些度很小但是很重要的“桥接”节点，它们在信息的传递中担任重要的角色[11]。第三，识别会受到网络中类核（Core-like）的影响[12]，这些类核结构里的节点对信息或者病毒的扩散能力通常较弱，但却会被识别为处在网络核心位置。第四，排序结果太过粗粒度，节点的区分度不大，尤其是在树形结构网络和无标度网络中。第五，未考虑节点在不同时间自身的传播属性。因此，本文从以上5个角度出发，通过在K壳分解原理的基础上，利用节点及其邻居的聚集性和扩散性，并结合节点传播状态的时序变化优化计算节点结构洞约束值，以K壳值与结构洞约束值联合评价作为节点重要性指标。通过在真实的网络中进行仿真验证，结果表明，该算法识别的关键节点对于网络鲁棒性的影响较大，从这些关键节点传入的信息能够在网络中更快地传播，并且传播范围更广。

1  基础理论

1.1  网络定义

对于一个无向无权网络，可以通过G=（V，E）进行表示，其中V表示网络中节点的集合，E是网络边的集合。eij用于表示节点i和节点j之间边的关系，如果节点i与节点j有边，则eij=1，否则eij=0。节点i的度表示为ki。为便于理论分析和实验验证，本文所用到的网络为静态网络，即网络中的节点数量及节点间关系不会随时间发生变化。

1.2  K壳分解算法

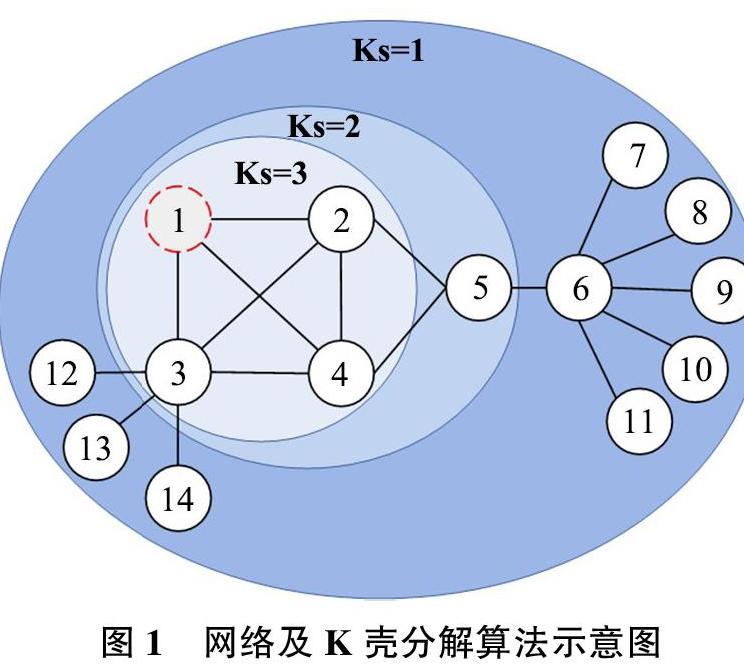
K壳分解算法可用于确定网络中节点的位置。其核心思想是根据节点度数递归地删除网络中的节点，分解过程如下：网络中如果存在度为1的节点，从度中心性的角度看它们就是最不重要的节点，删除这些节点及其相连的边，剩下的网络中会新出现一些度为1的节点，再将这些度为1的节点去掉，循環直至所剩的网络中没有度为1的节点为止，记这些删除的节点称为1。按上述方法继续剥壳，重复这些操作直到网络中没有节点为止。图1为经K壳算法分解后的网络示意图，其中1～3为3壳节点，5为2壳节点，6～14为1壳节点。

1.3  结构洞理论及网络约束值

社会学理论中，结构洞存在于社会网络中没有冗余连接的两个个体之间，洞两边的个体可以带来累加的网络收益[5]。从复杂网络的角度来看，结构洞特征强的两个节点之间的边在网络中能够获得更多竞争优势，是约束信息传播的关键边。Burt R S首先提出了用约束系数来衡量网络节点受到结构洞的约束，其表达式如下：

Ci=∑j∈τ（i）pij+∑qpiqpqj2， q≠i，j（1）

其中pij表示节点i为维持与节点j的邻居关系所投入的精力占总精力的比例（也就是度），piq和pqj分别是节点i、j与共同邻居q维持关系投入的精力占其总精力的比例。约束系数综合考虑了节点的邻居数目以及邻居之间连接的紧密程度（邻居间的闭合程度），节点邻居数量越少且与其邻居间的闭合程度越高，越不利于信息传播。

1.4  SIR疾病传播模型

疾病传播是社交网络上信息交换并可能传播的一种抽象表现形式，其传播是一个非常复杂的问题，结果依赖于传播过程中的具体情况。由于存在着这种相似性，学术界关于谣言传播模型的研究大多来源于经典的疾病传播模型。疾病传播模型最初是Kermack[13]在研究黑死病时提出的SIR模型。该模型描述了有些疾病的传播是具有免疫能力的，人被感染后就不会再次被感染。SIR模型将疾病流行范围内的人群分成易感者S，感染者I和免疫者R，人群中每个个体的时序状态在3类之间转换。在疾病演进过程中，处于感染态的节点以概率β向相邻的易感节点进行传播，同时每个感染节点则以概率γ治愈或死亡。

SIR模型适用于典型的社交网络舆情传播场景，针对一条信息，社交网络中的人群可分为不知情者S、知情并传播者I和知情不传播者R，通过SIR模型可动态描述信息在社交网络中的演进过程。

2  社交网络关键节点识别改进算法及算法论证

2.1  理论及算法

从上述相关理论分析可以看到，K壳分解算法可以高效地识别出节点所处的网络位置，“结构洞”约束值可从节点局部拓扑分析邻居节点之间的相互作用，节点传播状态可以从时间演进角度对舆情传播中的节点重要性进行评估。本文所提出的改进算法（Extended K-shell Based on Improved Network Constraint）综合考虑了K壳分解算法、优化后的“结构洞”约束值计算方法以及结合了节点传播状态的时序特征，更适用于社交网络的关键节点识别，算法定义如下：

KiCi（t）=ksi·ICi（t）（2）

KiCi（t）表示节点i在t时刻的KiC系数，ksi是节点i的K壳值，ICi（t）是本文优化后的节点i在t时刻的约束系数。从式（2）可以看出，KiC是t时刻由K壳值与约束系数点乘得出，因此该值既能够体现出节点的网络位置，又能够结合邻居的拓扑结构和时间维度上的传播状态。网络约束系数（Improved Constraint）的表达式为：

ICi（t）=TFi（t）·∑j∈τiTFj（t）·pij+∑k∈τjTFk（t）·qij·qjk， k≠i，j（3）

在Burt R S提出的算法中，通过节点的邻居数目（度）以及邻居之间连接的紧密程度（邻居之间的闭合程度）计算约束系数来识别关键节点，该算法应用在社交网络中存在3个问题：一是用节点度的大小来衡量节点是否处于社团的局部中心性不够全面;二是仅使用一阶邻居的闭合情况无法准确发现一些重要的“桥”节点;三是只考虑了网络空间特性，未考虑舆情演化的时间特性。因此，本文改进了约束系数的计算方式，通过边的聚集性代替度表示节点的局部中心性，通过边的二阶扩散性代替邻居闭合程度解决了“桥”节点识别不准的问题，通过节点的当前传播状态还原不同时序下节点的真实重要性。

式（3）中τi代表了节点i的邻居节点的集合，pij定义为边eij的聚集系数，qij定义为边eij的扩散系数，TFi（t）表示节点的时间演化因子（Time Evolution Factor）。其中：

pij={k∶k∈τ（i，j）＼i，j，Δijk∈ΔG}τ（i，j）＼i，j（4）

qij=∑k∈τ（i，j）＼i，jθkτ（i，j）＼i，j（5）

TFi（t）=1， t时刻i状态为S

1+β， t时刻i状态为I， β为传播概率

0， t时刻i状态为R（6）

1）边eij的聚集特性[14-16]可通过节点i和j的邻居节点与eij构成的三角形的占比来表示，无法构成三角形的邻居节点占比表示边eij的聚集特性。如图2所示，当信息从节点i经过边eij传播时，可通过扩散特性中的节点2和节点3将信息传播到网络中的其他节点，也可通过聚类特性中的节点1回传至节点j，因此边的聚类与扩散特性通过点的二阶邻居信息，有效地描述了对信息传播的影响作用。

2）时间演进因子TFi（t）表示在舆情演进过程中，i节点在t时刻所处的不同状态对节点约束系数正向促进或负向抑制的作用。本文认为S状态为节点的基础状态，在某时刻不知情状态（S状态）的节点将不会对约束系数起到作用;当节点处于I状态时，由于该节点当前具有传播性，因此会比网络空间中的其他节点更加重要，此时与该节点重要性相关的约束系数会加强;当节点处于R状态时，该节点当前及之后的时间将不会对信息进行传播，因此从舆情传播的角度来看该节点重要性降为0。

通过上述表述可知通过式（3）的改进，在约束系数的计算中同时体现了节点的聚类性、邻居拓扑结构的扩散特性以及节点当前时刻状态对节点重要性的加强和削弱作用。

2.2  算法论证

本文所提出的KiC算法相较以往的K壳及其改进算法，能够从空间上以低时间复杂度识别一些重要的“桥节点”，能夠有效消除类核（局部聚类结构）的影响，能够更加细粒度、有区分度地识别节点的重要性，能够随着信息的传播从时间维度识别关键节点。本节以图1所示的小规模数据集为例，进行算法准确性分析，为保证实验结果的可对比性，论证一至论证三只考虑网络空间特性而不考虑时间特性，即网络是一个所有节点都处于S状态的静态网络;论证四中节点2为初始信息传播者（I状态），其余节点为不知情者（S状态），传播率β为0.41（网络的平均度=2.43，为保证传播能够进行，取传播率为1k），康复率γ为0.1。

论证一：提供细粒度化关键节点识别能力。针对图1的网络，本文分别用几种算法对其分解，进而获得了节点重要性的排序结果。表1所示的是节点重要性排序结果。从表中可以看出，度中心性、K壳分解、MDD分解存在大量排序相同的节点，区分度相对较低。EKSDN（点权中心性）、结构洞算法相对较好，本文提出的KiC算法相较上述两种算法区分度更大，相比于其他算法效果稍好。

论证二：能够有效过滤影响力较低的类核节点。类核节点是指局部与大量节点紧密相连，而与网络中其他节点连接较少的节点。通过类核节点的信息更容易在这个紧密社团内部扩散，而不容易将信息扩散出去，因此将其识别为影响力最大的节点是不准确的。表1的结果可以看出，传统的K壳分解算法和结构洞算法将节点1识别为最重要节点。

本文提出的算法可以从节点1、2、3和4组成的相互紧密连接的类核中过滤出影响力较小的节点1。因此本算法在过滤类核方面优于传统算法。

论证三：能够发现重要局部“桥”节点。KiC算法综合考虑了节点的聚集性和扩散性，使既有桥接特性也具有社区中心性的节点2和4排名靠前，同时本文提出的算法通过从局部二阶节点的角度来衡量节点的“桥”特征，使得能够识别出更重要的“桥”节点5，观察图1可知，将节点2和4排在首位，将“桥”特性明显的节点5排在节点1前显然更加合理，所以KiC算法在识别“桥”特性方面优于其他算法。

论证四：能够随着信息的传播从时间维度更加准确地识别关键节点。观察图3，在t=1时刻节点2为初始信息传播者，该节点既具备最重要的网络空间特性，又是该时刻唯一信息传播者，被识别为关键节点。随着信息的传播，在t=2时刻节点2变为R状态，节点3和节点5变为I状态，由于节点2不再具备传播特性，从舆情传播的角度来看，该节点重要性降为0，节点3变为最重要节点。当t=3时，由于节点6变为信息传播者，增强了节点5的信息传播特性，根据算法计算结果此时刻节点5重要程度超过节点3。在t=4时刻，由于节点6变为了R状态，此刻节点3重新变为最重要节点。从信息传播的时间维度来看，相较于静态空间网络，KiC算法充分结合网络时空特性，能够有效地根据节点的不同传播状态动态识别关键节点。

3  实验与结果分析

3.1  数据集及信息传播模型

在实验中采用的网络为：①Karate网络[17]，美国一个大学空手道俱乐部成员;②Dophins网络[18]，以声音相互联系的海豚社交网络;③Polbooks网络[19]，美国政治书籍网络;④Football网络[20]，经典的美国橄榄球俱乐部社会网络;⑤NetScience网络[21]，从事网络理论和实验科学家合著的关系网络。表2为这5个网络的一些统计特性。

3.2  剔除关键节点后网络结构统计特性对比分析

为了验证关键节点对信息传播的影响，本实验使用KiC算法对5个真实网络的关键节点进行识别，并分别将识别出的排名前3%的关键节点隔离（剔除与这些节点相连的边）。网络结构的统计特性变化情况如表3，从表中可见，网络的平均度和聚类系数有所降低，平均路径长度有所增加。从信息传播角度分析，聚类系数的降低使得网络社团紧密度降低，信息在社团内部传播阈值将随之降低，而平均路径长度的提升使信息更难传播到网络的其他部分。从网络统计特性的角度验证了控制KiC算法所识别的关键节点对抑制信息传播的有效性。

3.3  关键节点对网络鲁棒性影响的分析

为了进一步分析KiC算法识别的节点的重要性，本组实验分别通过KiC、度中心性、K壳、接近中心性、介数中心性和随机6种算法将Karate网络的所有节点按照重要性进行排序，然后按照重要性从大到小的顺序依次移除节点，通过对比网络中剩余节点所构成的最大连通子图的节点个数，评估不同算法在识别关键节点的差异。从信息传播角度来看，移除相同节点，最大连通子图变化越大，说明图的连通性越差，信息传播到网络其他部分的可行性越低，移除的节点越重要。从图4可知，初始时刻Karate网络是一个完全连通的网络，开始移除节点后，通过随机算法移除节点的网络变化较小，而其他5种算法移除关键节点后最大连通子图变化明显，其中KiC算法、介数中心性、接近中心性相较度中心性和K壳算法下降较快。当移除重要性前5%的节点时，5种算法的最大连通子图分别为初始时刻的76%、69%、79%、83%、85%，而当移除重要性前12%的节点时，最大连通子图分别较移除5%时下降36%、36%、32%、21%、22%至49%、44%、52%、83%、84%。通过实验数据可知KiC算法所识别的关键节点较K壳算法和度中心性算法更加准确，与介数中心性和接近中心性相近，KiC、介数中心性、接近中心性在控制10%左右的重要节点后最大连通子图降至50%左右，能够有效地降低网络连通性，降低信息传播能力。

3.4  网络传播动力学模型有效性验证

为了验证KiC算法识别的重要节点在社交网络上的传播能力，本节通过在真实社交网络上使用SIR模型模拟信息传播，对比不同信息传入节点平均信息传播范围和平均传播速度来考察节点的真实影响力。本实验共设置5组，对应5个不同的真实社交网络，每组实验设置一个对照组，分别以KiC算法识别的最重要节点和随机选取一个节点为初始感染节点，观察每一时间步网络中感染过的节点数目和最终稳定态时感染过的节点数目，为保证传播能够进行，取SIR模型中传播率为1k，康复率为0.1。

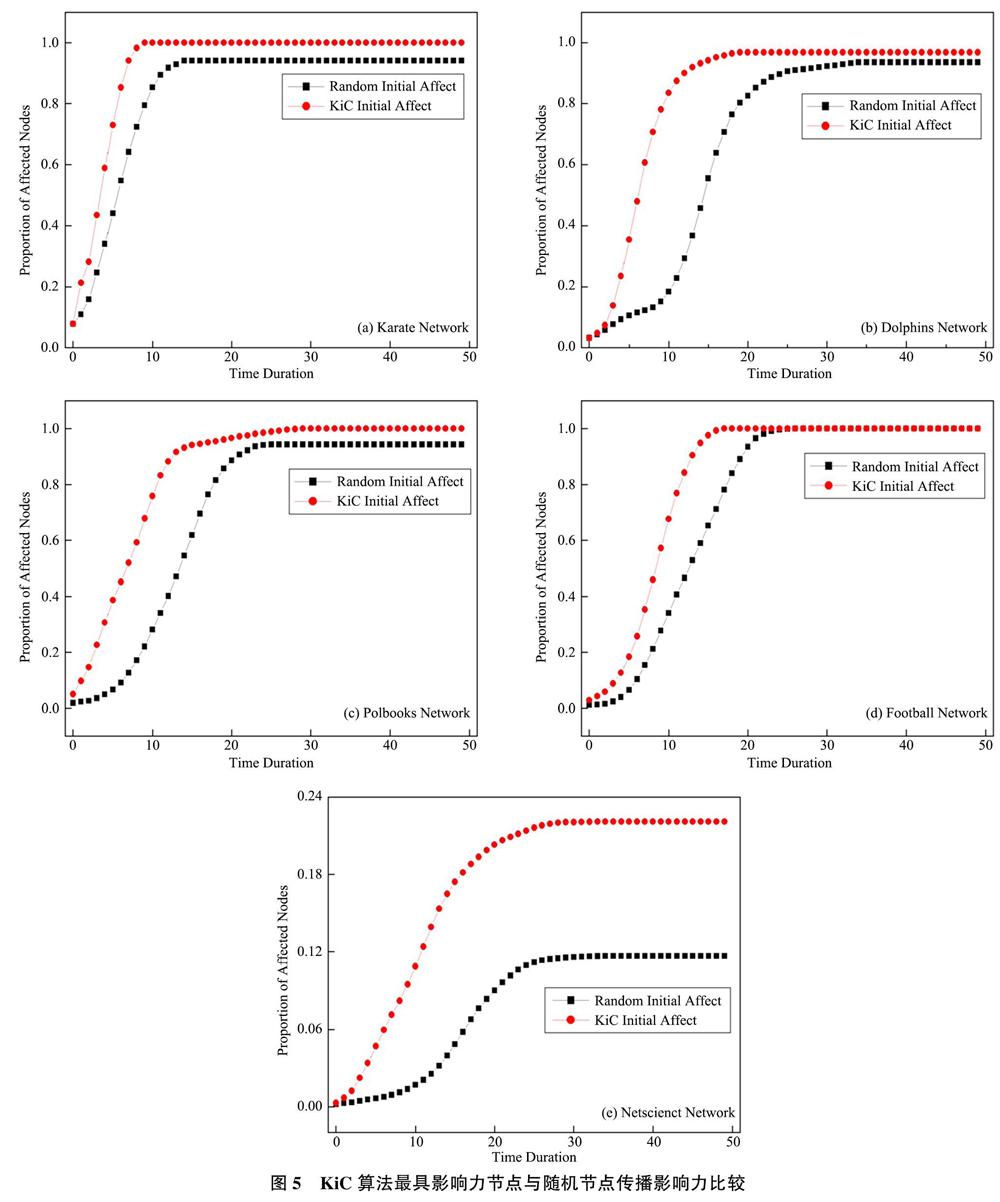
通过对比图5中的5个真实网络的传播情况可以发现，整体上看对于各个传播时间t通过KiC算法识别的重要节点传入的信息，其传播范围都明显大于随机传入网络的信息，并且最终稳定状态下受到信息影响的节点数量较多，其中Karate网络多6.2%，Dolphins网络多3.4%，Polbooks网络多6%，Football网络持平，NetScience网络多89%。同时从图5曲线斜率看，传播到达稳态之前通过KiC算法识别的节点传入的信息斜率要高于随机节点传入，表明本文提出的算法所识别的节点网络信息扩散速度较快。通过以上实验可知，以KiC算法获得的节点为初始感染源的传播又快又广，说明本算法能够识别网络中传播影响力高的节点。

4  总  结

在大规模社交网络中快速搜索关键节点对于信息的引导和传播控制具有重要的意义。实践表明，社交网络舆情传播不同于传统的复杂网络，具有明显的时空特性，在空间方面，要准确识别规模性社交網络中不同节点的传播能力，既要考虑节点所处的网络位置和邻居的拓扑结构，同时需兼顾计算的时间复杂度;在时间方面，要结合网络中节点的传播状态进行综合评判。基于以上考虑，本文提出一种结合节点局部中心性特征的K壳改进算法（KiC算法），该方法利用节点的聚集性特征及其邻居的扩散性特征，并结合节点传播状态的时序变化作为改进后的“结构洞”约束值，综合K壳算法对节点所处位置的高效识别能力，作为评价节点重要性的指标。该改进方法同时考虑了节点的自身属性、所处的网络位置及其局部拓扑、不同时刻节点传播状态属性，评价结果更加全面高效。

实验结果表明：①该算法在网络结构上能够消除类核影响，细粒度的识别重要的“桥节点”，并充分结合网络时空特性，有效地根据节点的不同传播状态动态识别关键节点。②移除该算法所识别的重要节点后，网络聚类系数降低、平均路径长度增加，这些网络特征的变化能够控制信息传播范围的扩大。移除该算法所识别的10%的重要节点，能够将网络最大连通子图的节点数降低50%，对于网络鲁棒性的影响与介数中心性、接近中心性接近，但其计算仅基于节点局部信息，时间复杂度低。③通过基于SIR模型的信息传播验证，以该算法识别的重要节点为初始传播源可提升信息传播范围和平均传播速度，以Karate网络为例，其传播范围平均扩大6.2%，到达最大影响范围时传播时间平均缩短50%。

本文所提出的KiC算法是通过经典社交网络进行仿真验证的，但我们相信本文所做的研究对于政府决策部门对舆情的扩散和控制具有一定的参考价值。后续我们将重点根据实验仿真结果抓取真实社交网络数据进行验证。

参考文献

[1]Bonacich P.Factoring and Weighting Approaches to Status Scores and Clique Identification[J].Journal of Mathematical Sociology，1972，2（1）：113-120.

[2]Freeman L C.A Set of Measures of Centrality Based on Betweenness[J].Sociometry，1977，40（1）：35-41.

[3]Latora V，Marchiori M.Efficient Behavior of Small-World Networks[J].Physical Review Letters，2001，87（19）.

[4]Chen D，Lu L，Shang M，et al.Identifying Influential Nodes in Complex Networks[J].Physica A-statistical Mechanics and Its Applications，2012，391（4）：1777-1787.

[5]Burt R S.Structural Holes：The Social Structure of Competition[M].Cambridge，MA，USA：Harvard Univ，Press，2009.

[6]苏晓萍，宋玉蓉.利用邻域“结构洞”寻找社会网络中最具影响力节点[J].物理学报，2015，64（2）：5-15.

[7]Ruan Y，Lao S，Xiao Y，et al.Identifying Influence of Nodes in Complex Networks with Coreness Centrality：Decreasing the Impact of Densely Local Connection[J].Chinese Physics Letters，2016，33（2）.

[8]Kitsak M，Gallos L K，Havlin S，et al.Identification of Influential Spreaders in Complex Networks[J].Nature Physics，2010，6（11）：888-893.

[9]Zeng A，Zhang C.Ranking Spreaders By Decomposing Complex Networks[J].Physics Letters A，2013，377（14）：1031-1035.

[10]王环，朱敏.基于点权的混合-shell关键节点识别方法[J].华东师范大学学报：自然科学版，2019，（3）：101-109.

[11]Cheng X，Ren F，Shen H，et al.Bridgeness：A Local Index on Edge Significance in Maintaining Global Connectivity[J].Physics，2010，（5）.

[12]Liu Y，Tang M，Zhou T，et al.Core-like Groups Result in Invalidation of Identifying Super-spreader By K-shell Decomposition[J].Scientific Reports，2015，5（1）：9602-9602.

[13]Pastor-Satorras R，Vespignani A.Epidemic Spreading in Scale-Free Networks[J].Physical Review Letters，2001，86（14）：3200-3203.

[14]Malliaros F D，Rossi M G，Vazirgiannis M，et al.Locating Influential Nodes in Complex Networks[J].Scientific Reports，2016，6（1）：19307-19307.

[15]杨李，宋玉蓉，李因伟.考慮边聚类与扩散特性的信息传播网络结构优化算法[J].物理学报，2018，67（19）：92-102.

[16]Liu Y，Tang M，Do Y，et al.Accurate Ranking of Influential Spreaders in Networks Based on Dynamically Asymmetric Link Weights[J].Physical Review E，2017，96（2）.

[17]Zachary W W.An Information Flow Model for Conflict and Fission in Small Groups1[J].Journal of anthropological research，1976，33（4）：452-473.

[18]Lusseau D，Schneider K，Boisseau O，et al.The Bottlenose Dolphin Community of Doubtful Sound Features a Large Proportion of Long-lasting Associations[J].Behavioral Ecology and Sociobiology，2003，54（4）：396-405.

[19]V Krebs.http：//www.orgnet.com/[EB].

[20]Girvan M，Newman M E.Community Structure in Social and Biological Networks[J].Proceedings of the National Academy of Sciences of the United States of America，2002，99（12）：7821-7826.

[21]Newman M E.Finding Community Structure in Networks Using the Eigenvectors of Matrices[J].Physical Review E，2006，74（3）.

（责任编辑：陈  媛）