考虑不确定性因素影响的不同桥梁构件地震易损性分析

周 冬

(陕西铁路工程职业技术学院,陕西 渭南 714099)

地震会给人类带来巨大的生命财产损失,如何增加建筑物的抗震性能,对于工程界和科学界而言一直是一个热门话题,从而促进了工程结构抗震理论的发展,经过多年的发展和完善,基于性能的地震工程和抗震设计逐渐被广大工程界人士接受和采纳[1-3]。但是,由于人类目前对地震的了解以及其他领域知识的局限性,造成了对于事物本身认知的随机性和不确定性,如何将这些随机性和不确定性进行量化研究[4-6],成为提高建筑物抗震设计的一大趋势,这就是所谓的地震易损性分析,其将概率论和不确定因素相结合,最终得到不同不确定因素影响下地震的损失量化评估[7]。

21世纪以来,我国的基础设施建设取得了飞跃式发展,其中,桥梁总长度已跃居世界第一,一批地处地质复杂区的特高、特大、特长桥梁相继建成通车,给我国经济建设注入新的活力。但是因我国地处环太平洋和欧亚地震带交界中心,地震发生频率较高,这就更需要做好桥梁结构的抗震设计,做好地震灾害损失评估,提高桥梁的抗震设防标准。前人研究表明:桥梁所处的地质环境、水文环境以及本身的结构形式等均会对地震易损性产生影响[8-11],这些因素均是通过勘察、测量、试验等可获得的确定性因素;当考虑一些不确定和随机因素时,往往会利用概率和相关理论,冯清海[12]、吴文朋等[13-14]、李立峰等[15]均对不确定和随机变量影响下的桥梁易损性做了初步的分析,得到了一些对现场设计施工有用的结论。

在前人研究经验和理论基础上,以陕西某双幅高速公路桥梁为分析对象,采用正态分布、对数正态分布以及均匀分布3种概率分布形式,结合不同构件的损伤状态和不确定性,对6种工况下的桥梁地震易损性进行了分析,以期为工程实践提供帮助。

1 工程背景

陕西西安某桥梁为一座双幅高速公路桥梁,跨径形式为4×30 m=120 m,属双向6车道路面,桥梁宽度为43 m(单幅桥宽19 m,中央隔离带5 m),桥梁纵向坡度为1.2%,横向坡度为2%。桥梁上部结构由8片预应力T型梁组成,混凝土强度为C40,下部结构为10 m高的排架墩(3×1.4 m圆柱+2 m×1.6 m矩形盖梁),材料为C30混凝土,桥台主要为桩基支撑的座式桥台,为9.7 m,桩基深度约为8.5 m,支座包括铅芯橡胶支座和板式橡胶支座,桥梁的布置结构形式见图1。

图1 桥梁的结构布置形式示意(单位:cm)Fig.1 Structure layout of the bridge (unit:cm)

2 工况及分析过程简介

2.1 工况及构件设置

将建模分析的相关参数进行分类:结构层次类不确定性参数(SU,uncertainty parameters of hierarchical structure)、材料层次类不确定性参数(MU,uncertainty parameters of material hierarchy)以及边界条件类不确定性参数(BU,uncertainty parameter of boundary condition class),地震波不确定性表示为(RTR,only consider the record-to-record),全要素表示为(ALL,uncertainty of all modeling related parameters),关键要素表示为(KEY,uncertainty of key related parameters),共设置6种工况,见表1。计算对象主要考虑桥梁的桥墩、板式支座、铅芯支座以及桥台4种构件,损伤状态分为:轻微损伤、中度损伤、严重损伤以及完全破坏4类。

表1 工况计算说明

2.2 分析过程

桥梁地震易损性分析中,首先假定抽样次数等于地震波数,其计算流程如下:(1)选取工程算例原型,分析需要考虑的不确定性因素,假设有k个不确定因素[X1,X2,X3,…,Xk];(2)确定不确定因素的概率分布模型,一般包括:正态分布、对数正态分布以及均匀分布3种概率分布形式;(3)将地震波信息输入模型,确定地震波数量N和地震强度参数IM;(4)根据概率分布函数,进行N次分层抽样,得到N个参数样本,建立有限元分析模型;(5)将有限元分析模型与地震波随机组合,获得地震波IM值和工程需求参数的最大响应值;(6)确定不同构件的损伤极限状态和不确定性;(7)建立不同构件的概率地震需求模型,计算不同构件的损伤超越概率,获得地震易损曲线,结合构件的极限损伤指标,构建起地震易损性函数,计算强度均值、标准差,探讨各因素对易损性的影响[16]。

地震易损性函数为

P[D≥DSi|IM]=

(1)

其中:DSi表示第i种损伤状态下的损伤指标值;IMmi表示第i种损伤状态下的地震强度均值;a、b表示计算回归参数;ζβi表示修正的对数标准差(离差);βD|IM表示桥梁构件的总的不确定性;βCi表示对数标准差。

3 结果分析

3.1 不同构件失效概率分析

不同极限损伤状态下,桥梁构件的失效概率曲线与普加速度的关系(易损曲线)见图2。从图2中可以看到:不同损伤状态下,构件的易损曲线特征不尽相同,从轻微损伤的“S”型逐渐转变为完全破坏时的“指数”型;在轻微损伤、中度损伤以及严重损伤状态下,相同普加速度时,铅芯橡胶支座的失效概率最大,而在完全破损状态下,板式橡胶支座的失效概率最大,这是因为桥墩侧向抗推刚度值要远小于桥台的刚性值,在地震波作用下,相对位移响应会大于板式橡胶支座及其他桥梁构件,但是在完全破损状态下,支座的破坏是由落梁破坏决定而非支座本身,由于其搭接长度的关系,造成破损状态下的易损性要小于板式橡胶支座;在4种损伤极限状态下,桥墩的失效概率值最低,这是因为桥墩的强度较大,刚度适中并且具有一定的变形柔性;从整体上看:算例桥梁构件未出现单个构件失效概率突变的情形,这是因为该桥梁采用了铅芯橡胶支座和板式橡胶支座相结合的布置方式,不仅减小了滑移给墩柱造成的损伤,还能通过铅芯支座来恢复主梁的变形及位移,进而提升桥梁的整体稳定性和抗震性。

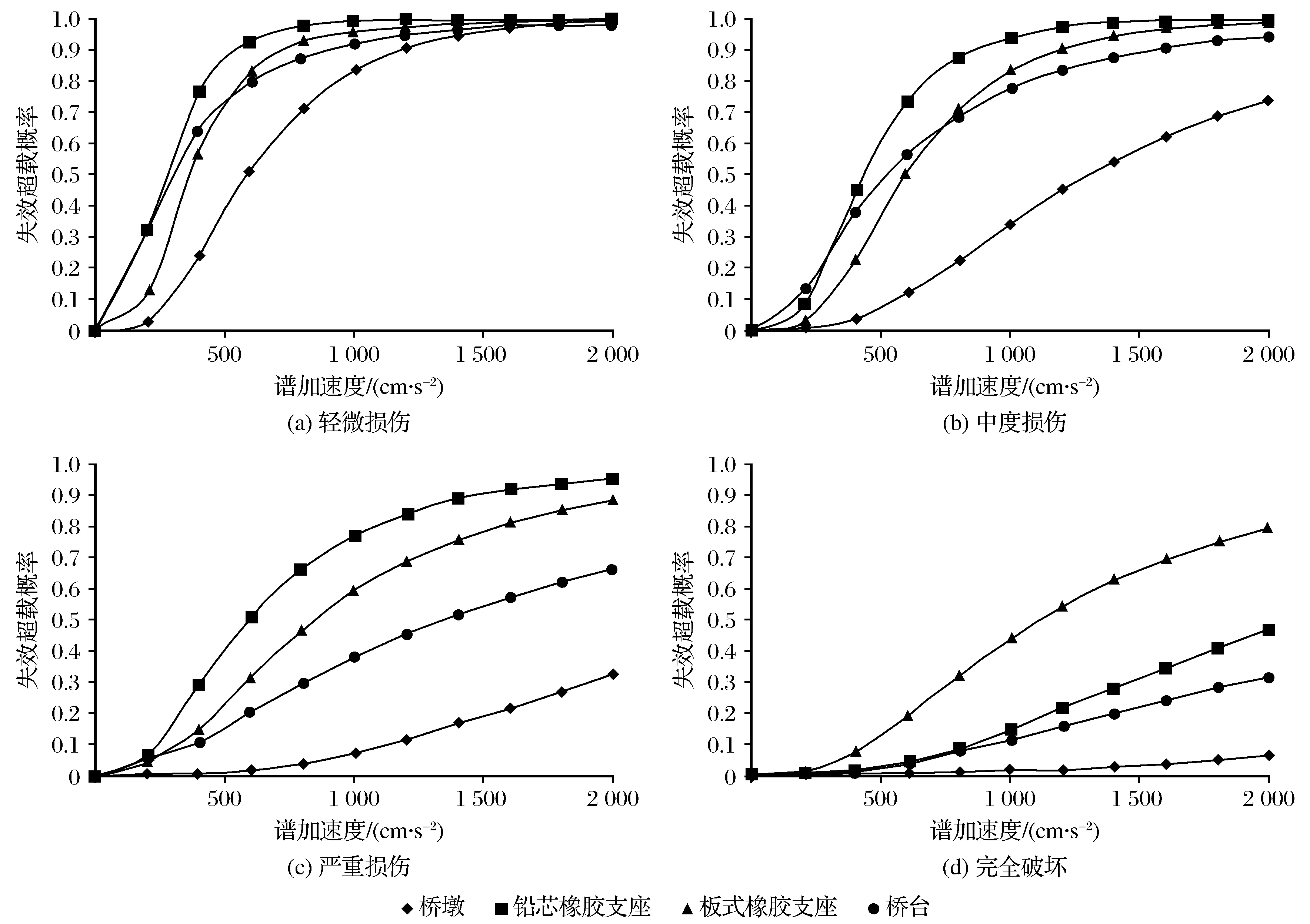
图2 不同构件易损性曲线对比Fig.2 Comparison of vulnerability curves of different components

相同损伤状态下(以中度损伤为例),不同工况下的失效概率值随谱加速度的关系(易损性曲线)见图3。从图3中可以观察到:不确定性因素对于桥墩和桥台的影响程度明显大于对支座的影响程度,改变不确定因素对支座的地震易损性较小;同一构件处,RTR+ALL与RTR+KEY工况下的概率失效值基本相等,表明全要素和关键要素的易损性大致相当,当应用于实际工程时,采用关键因素进行简化计算,可大大节省工程量[17];结构层次不确定性要素和材料层次不确定性要素对桥梁构件易损性的影响不大,但边界条件对桥梁构件的影响较大,其中:铅芯橡胶支座和桥台在仅考虑边界条件影响时,其失效概率反而大于全要素工况,这是因为同时考虑结构和材料层次时,二者会降低地震易损性,因此,全要素的易损性会低于仅考虑边界条件的易损性。

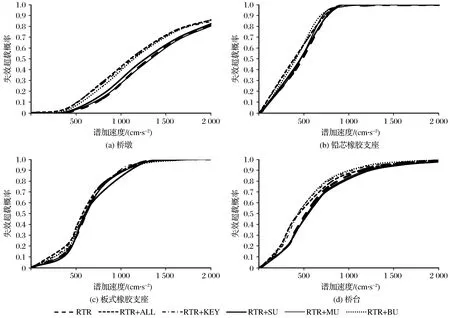
图3 不同工况下易损性曲线对比Fig.3 Comparison of vulnerability curves under different working conditions

3.2 不确定因素对构件易损性影响

不同工况下桥梁构件的易损性强度均值对比见图4。从图4中可以看到:在相同损伤极限状态下,RTR+ALL与RTR+KEY工况下的强度均值最小,且二者基本相当,再次表明了考虑关键因素和全要素的桥梁构件易损性基本一致,实际过程中可以利用关键因素代替全要素进行简化计算;轻微和中度损伤状态下,易损性强度均值大小基本表现为:桥墩>板式橡胶支座>桥台>铅芯橡胶支座,严重损伤状态下,易损性强度均值大小表现为:桥墩>桥台>板式橡胶支座>铅芯橡胶支座,完全破损状态时,易损性强度均值大小表现为:桥墩>铅芯橡胶支座>桥台>板式橡胶支座;RTR+SU与RTR工况相比,二者的强度均值基本相当,表明结构层次的不确定性影响相对较小;RTR+MU相较于RTR工况其强度均值略有增加,而RTR+BU相较于RTR工况其强度均值略有增加,特别是桥墩,下降幅度较为明显。

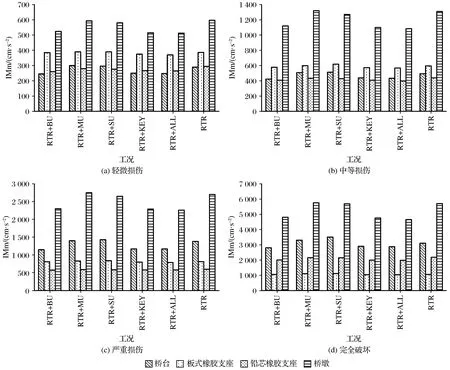
图4 不同工况下构建易损性强度均值对比Fig.4 Comparison of mean vulnerability strength under different working conditions

表2 桥梁不同构件易损性函数标准差(不确定性)对比

4 结论

(1) 不同损伤极限状态下,构件的失效超载概率差别较大,当在轻微、中等和严重损伤状态下时,铅芯橡胶支座的失效概率最大,当处于完全破损状态下时,板式橡胶支座的失效概率最大,这与落梁破坏有关。

(2) 边界不确定性对于桥梁构件易损性的影响程度大于结构和材料层次的影响,结构层次的影响基本可以忽略;工程实际应用时,可采用关键因子代替全要素进行简化计算。

(3) 桥梁各构件的不确定性离差差别较大,易损性函数度对数标准差取值范围较大(0.359～0.912),传统的组合离差取值方法不具有普适性,需视具体情况进行调整。