基于多重分析模型综合的深基坑稳定性评价及变形趋势判断
2020-12-17马敏杰罗绍仟
武 韬,马敏杰,罗绍仟
(国家林业和草原局昆明勘察设计院,云南 昆明 650216)
随着我国城市建设的不断发展,基坑工程数量也在不断增加。在基坑开挖过程中,支护结构及周边土体均会出现不同程度的变形,会对周边近接建、构筑物形成安全隐患[1-3]。因此,基坑变形监测及数据分析就显得格外重要。目前,变形监测是基坑施工安全监控的主要手段,国内外许多学者对其进行了大量研究。Laefer等[4]研究了不同地质条件下的基坑开挖对近接建筑物的影响;Seo等[5]对基坑开挖引起的周边地表沉降进行了预测,分析了基坑的沉降变形规律。同时王宁伟等[6]、张海云等[7]均基于现场监测数据,分析了基坑的变形规律和发展趋势,为现场施工提供了一定的依据;陈昆等[8]通过数值模拟分析了基坑开挖过程的变形特征,所得模拟结果与实测结果基本一致,为类似基坑设计提供了参考;黄沛等[9]针对敏感环境下的大基坑开挖,提出了地基加固与分区开挖相结合的变形控制措施,达到了预期效果;王飞等[10]通过现场监测数据,构建了基坑自身的风险评价体系,实现了基坑施工风险评价的定量判断,弥补了规范中风险评价的不足。上述研究虽取得了相应成果,但也缺少基坑施工过程中稳定性评价和变形趋势分析的综合研究;同时,基坑变形监测是为施工服务,进而监测数据的分析重点可放在基坑稳定性和变形趋势判断上,其中,稳定性可评价基坑的现有状态,而变形趋势可判断基坑稳定性的发展趋势。因此,研究基于尖点突变理论的稳定性判断能力、Bartels检验的变异判断能力及波动互相关分析的趋势判断能力,构建了基坑稳定性和变形趋势判断的综合检验体系,以期为工程施工提供一定的指导依据。
1 基本原理
1.1 研究思路
基坑变形监测是施工过程中的必要手段,但由于基坑所处地质条件的复杂性和施工过程的不确定性,使得变形监测数据蕴含了基坑内部系统的力学演化信息,具有复杂性和非线性。因此,单一方法难以实现基坑变形信息的综合分析,需结合多种方法进行综合研究。鉴于上述原因,作如下分析:
(1) 工况划分。基于现场监测结果,结合施工过程和开挖深度,对基坑变形过程进行工况划分;同时,分析不同检验水平下的变形速率置信区间,以掌握基坑变形速率的分布特征。
(2) 稳定性判断。利用尖点突变理论判断不同工况条件下基坑稳定性,再利用Bartels检验判断基坑稳定性的变异程度,以分析基坑稳定性的发展趋势。
(3) 变形趋势判断。利用波动互相关分析判断基坑变形的发展趋势,以验证稳定性分析结果的准确性。
1.2 尖点突变理论
突变理论可用于解决物理界和数学界连续系统中的不连续问题,是非线性理论的重要分支,其数学形式共包含7种类型,其中尖点突变模型的应用最为广泛。同时,尖点突变理论可以很好地评价事物由稳定状态至非稳定状态的转变过程,对评价基坑的稳定性具有较好的适用性[11-12]。
尖点突变理论在基坑稳定性判断中的应用步骤为:(1)基于基坑变形的现场监测数据构建变形函数;(2)对变形函数进行标准化处理,将其转变为尖点突变模型的标准函数形式;(3)求解标准函数的突变特征值,并判断基坑变形的稳定性。
利用Matlab的cftool工具箱对基坑变形数据进行四次多项式拟合,进而确定基坑的变形函数为
Ut=a0+a1t+a2t2+a3t3+a4t4,
(1)
其中:Ut为基坑变形函数;ai(i=0,1,2,3,4)为待拟合参数;t为时间节点参数。
同时,利用Tschirhaus变换将变形函数进行初步变换,即
Ux=b4x4+b2x2+b1x+b0,
(2)
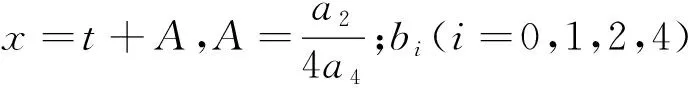
拟合参数a和变换参数b的关系式为
(3)
再对式(2)两侧同除以b4,即可得到尖点突变理论的标准形式为
U=x4+μx2+vx+c,
(4)
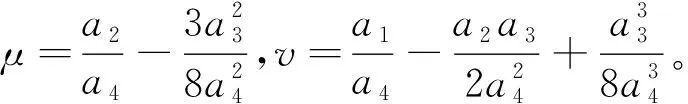
最后,对上式进行二次求导,可得突变特征值为
Δ=8μ3+27v2。
(5)
根据突变特征值即可判断基坑稳定性:当Δ>0时,基坑处于稳定状态;当Δ<0时,基坑处于不稳定状态。同时,突变特征值的大小可衡量基坑稳定性的强弱,即Δ>0时,其值越小,稳定性状态越好,反之稳定性状态越差[13]。
1.3 Bartels检验
Bartels检验是一种随机性检验,于1982年由Robert Bartels提出,其初步统计量[14]为
(6)
其中:RVN为Bartels检验的初步统计量;R′为秩次均值;Ri为第i个节点处的秩次;T为样本总数。
同时,RVN服从正态分布N(2,4/T),进而可得到Bartels检验的评价指标P值为
P=2×min(pnorm(RVN′),
1-pnorm(RVN′)),
(7)
(8)
其中:pnorm(*)为小于该数的概率值;min(*,*)为最小函数。
另外,根据P值大小可判定检验对象的变异程度,研究中将变异程度划分为3个等级,如表1所列。

表1 变异程度划分
由表1可知,P值越小,变异程度越高,说明基坑稳定性的变异可能性越高。
1.4 波动互相关分析
波动互相关分析的核心思想是利用两序列间的波动分析来评价两序列的相关性,以实现序列总体上的互相关影响程度评价。其分析过程如下[15]:
(1) 若两评价序列为{xi:i=1,2,…,N}和{yi:i=1,2,…,N},分别对两序列进行波动轮廓处理:
(9)
(10)
其中:vx(l)、vy(l)为两序列在l步长条件下的波动轮廓;l为波动轮廓的步长;x′、y′为两序列的平均值;N为序列长度。
(2) 计算各评价序列的波动平方根,计算公式为
Δvx(l,l0)=vx(l0+l)-vx(l0),
(11)
Δvy(l,l0)=vy(l0+l)-vy(l0),
(12)
其中:Δvx(l,l0)、Δvy(l,l0)分别为两序列在时间间隔为l时的统计差分;l0=N-l。
(3) 求解波动协方差Fxy(l),计算公式为
(13)
其中:l0=1,2,…,N-l;l=,1,2,…,N。
(4) 由于协方差与波动互相关系数hxy间存在幂函数关系,即
lnFxy(l)=hxy·lnl+lnC,
(14)
其中:C为待拟合常数。
(5)hxy为波动互相关系数,代表两评价序列间的相关程度。当hxy<0.5时,说明两序列呈负相关,即两序列的发展趋势相反;当hxy=0.5时,说明两序列不具有相关性;当hxy>0.5时,说明两序列呈正相关,即两序列的发展趋势相同。同时,hxy数值越大,表示两序列的相关性越强。
在基坑变形趋势的判断过程中,由于监测时间具有持续增加的特点,因此,确定波动分析的评价序列为监测时间序列和累计变形实测序列。
2 工程实例
2.1 工程概况
基坑位于上海市中心,拟建占地面积为6 800 m2,主楼局部最大开挖深度为15.3 m,裙房局部最大开挖深度为13.3 m,总计开挖方量为9.9万m3。支护结构包含地下连续墙和三道横撑,且横撑形式为钢筋混凝土。其中,地下连续墙的宽度为0.8 m,主楼局部最大深度为30.8 m,而裙房局部最大深度为26.8 m;三道横撑的中心标高分别为-11.25 m、-7.25 m和-2.1 m。
由于该基坑位于市中心,其周边近接建筑物较为复杂,加之周边地下管线较多(共计有14条,主要涉及燃气、电力、信息及给排水等管线),使得基坑开挖过程中的变形控制格外重要[16]。
根据勘查成果,基坑开挖深度范围内的土层主要有7个工程地质单元,以粉质粘土为主,且各土层的物理力学参数如表2所列。
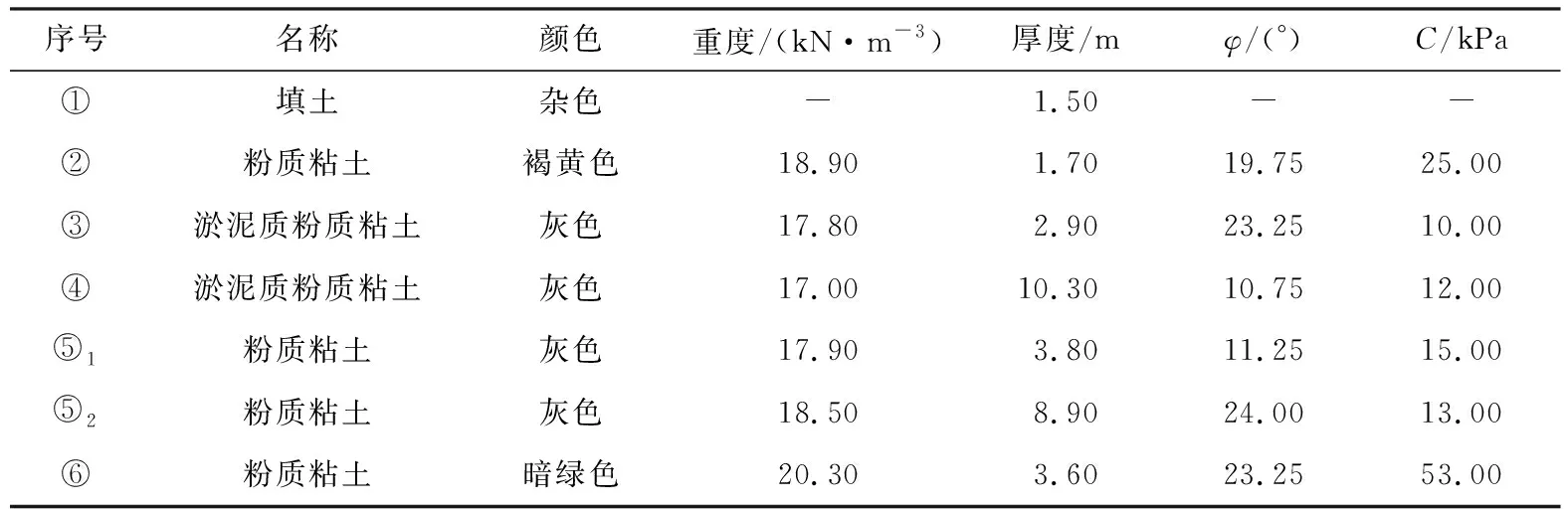
表2 土体物理力学参数
由于该基坑所处地段的地质条件较为复杂,使得该基坑的工程安全性较高,为确保施工安全及周边建筑物、管线的正常运营,对基坑进行了必要监测,其中,水平位移8#监测点处的基坑开挖深度为10 m,该监测点监测数据完整性和连续性较好,因此,研究主要对该点进行分析。8#监测点的监测时间为5月30日—8月23日,监测频率为1次/d,共计86个监测周期,其变形曲线如图1所示。同时,为便于基坑不同阶段的稳定性和变形趋势分析,结合施工阶段和开挖深度将监测样本划分为3个工况,分别为:
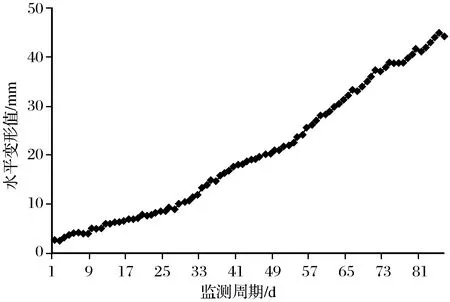
图1 8#监测点水平位移变形曲线Fig.1 Horizontal displacement deformation curve of 8# monitoring point
第1工况:该工况的基坑开挖深度为0~3.5 m,施工时间共计32 d,即监测数据为第1~32周期。
第2工况:该工况的基坑开挖深度为3.5~8 m,施工时间共计35 d,即监测数据为第33~67周期。
第3工况:该工况的基坑开挖深度为8~10 m,施工时间共计19 d,即监测数据为第68~86周期。
为进一步分析基坑的变形特征,再对基坑变形速率的变化特征和分布特征进行统计,且基坑水平位移变形速率为正时,基坑水平位移向内变形,反之向外变形,基坑变形速率曲线如图2所示。
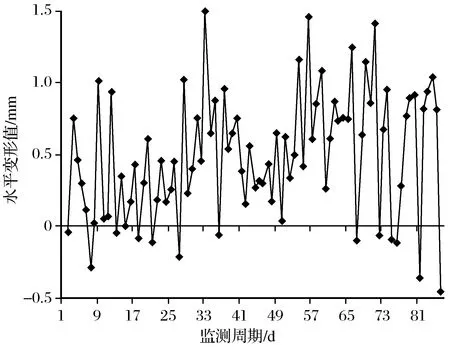
图2 8#监测点水平位移速率曲线Fig.2 Horizontal displacement rate curve of 8# monitoring point
由图2可知,基坑变形速率的波动性较强,且多以正值为主,说明基坑水平变形多向内侧变形。同时,再对基坑水平位移速率特征参数进行统计,如表3所列。由表3可知,在不同工况条件下,变形速率的特征参数是具有差异的,说明基坑变形特征的分阶段研究具有必要性。在变形速率的均值方面,以第2工况的变形速率平均值最大,其次是第3工况和第1工况;而在变形速率的稳定性方面,以第3工况的方差值最大,其次是第2工况和第1工况,说明随着基坑开挖深度的增加,基坑变形将会加剧,且变形的波动性也将会增强。
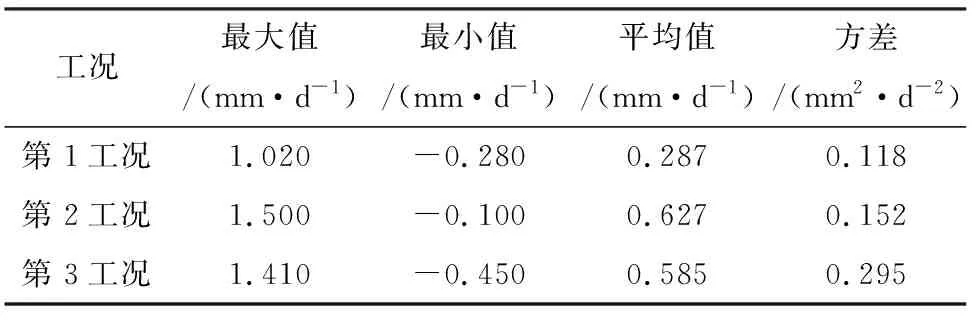
表3 8#监测点水平位移速率特征参数
另外,再利用正态分布及t检验的基本原理,对基坑水平位移速率的置信区间进行求解,置信区间的求解公式为
(15)
其中:z′为平均变形速率;s为变形速率序列的均方差;n为速率序列的样本总数;ta(n-1)为自由度,为n-1和显著水平为a时的临界值。
根据式(15),在不同置信水平条件下,对基坑水平位移速率的置信区间进行求解,结果如表4所列。根据表4,可以确定相应置信水平条件下基坑水平变形速率的变化范围,当出现奇异值时,可重新测量或加强监测频率,以便更好地指导现场监测。
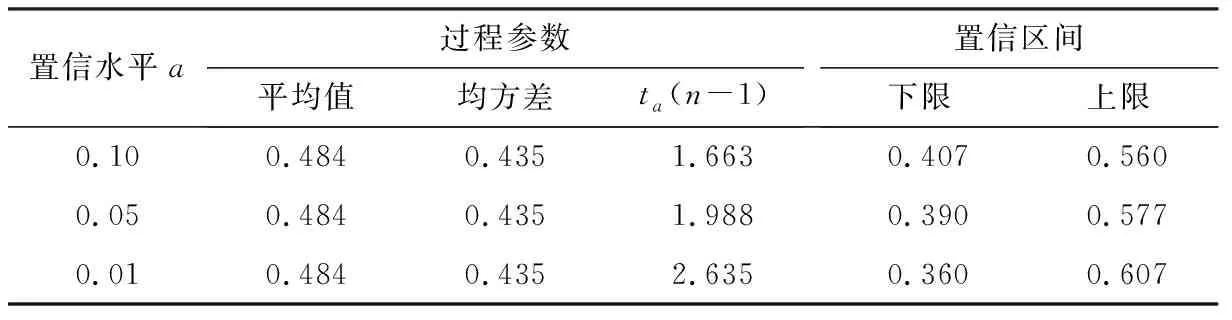
表4 水平位移速率的置信区间统计
2.2 稳定性分析
结合前述尖点突变理论的基本原理,采用Matlab的cftool工具箱对各工况的监测成果进行四次多项式拟合,结果如表5所列。由表5可知,各工况拟合结果的拟合度均趋近于1,均方根误差也较小,说明各工况的拟合结果较好,其中,以第3工况的拟合结果相对略优,其次是第2工况和第1工况。

表5 各工况的多项式拟合结果
同时,对各工况的突变参数和突变特征值进行求解,过程如下:
第1工况:
μ1=-2.177×102,v1=1.355×104,
则Δ1=4.874×109>0;
第2工况:
μ2=2.836×103,v2=4.148×105,
则Δ2=4.829×1012>0;
第3工况:
μ3=-6.304×103;v3=-5.153×105,
则Δ3=5.166×1012>0。
根据上述可知,随基坑开挖深度的增加,突变特征值相应增加,说明基坑稳定性随开挖深度的增加而减弱,与实际情况相符;第2工况突变特征值较第1工况突变特征值的增量较大,而第3工况突变特征值较第2工况突变特征值的增量较小,说明第2工况的稳定性减弱程度相对较大,而第3工况的稳定性减弱程度相对较小;由于基坑各工况的突变特征值均大于0,说明基坑目前仍处于稳定状态。
为进一步分析基坑稳定性的发展趋势,利用Bartels检验判断基坑稳定性的变异趋势,检验结果如表6所列。
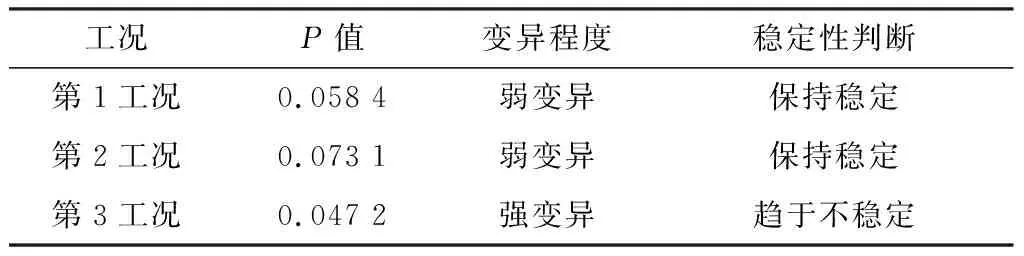
表6 基坑稳定性变异程度检验
由表6可知,第1工况的稳定性变异程度为弱变异,说明第2工况的稳定性与第1工况一致,仍将保持稳定状态;第2工况稳定性变异程度为弱变异,说明第3工况的稳定性与第2工况一致,仍将保持稳定状态,上述两工况的检验结果与尖点突变理论的分析结果一致,说明Bartels检验结果的可信度较高。同时,第3工况的变异程度为强变异,说明基坑后期的稳定状态较第3工况的稳定状态会出现变异,即往不稳定方向发展。
2.3 变形趋势分析
据研究思路,为验证稳定性分析结果的准确性,利用波动互相关分析判断基坑的变形趋势,分析结果如表7所列。由表7可知,在各工况的波动互相关分析过程中,拟合度均趋近于1,而均方根误差均较小,说明各工况的拟合结果较优,为hxy指数的准确求解奠定了基础;第1工况的hxy指数大于0.5,得出基坑第2工况的变形将呈持续增加趋势,且第2工况的hxy指数也大于0.5,得出基坑第3工况的变形也将呈持续增加趋势。上述两工况的趋势判断结果均与图1基坑变形曲线的发展趋势相符,验证了波动互相关分析结果的准确性。同时,第3工况的hxy指数为0.796,说明基坑后期的变形发展趋势仍将增加,加之基坑累计变形量已达44.29 mm,已趋近于变形控制值,说明基坑稳定性将向失稳方向发展,与前述的稳定性分析结果一致。
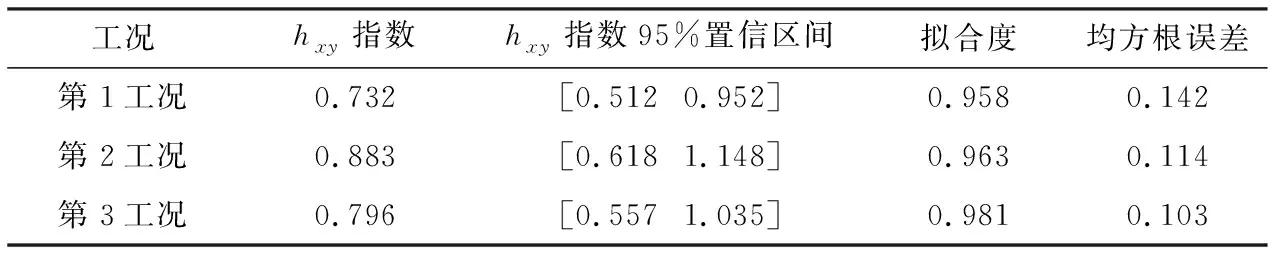
表7 变形趋势分析统计
综上所述,基坑的稳定性分析结果与变形趋势分析结果具有较好一致性,验证了尖点突变理论、Bartels检验和波动互相关分析在基坑工程应用中的有效性。
3 结论
研究以尖点突变理论、波动互相关分析和Bartels检验为理论基础,构建了基坑稳定性和变形趋势判断的综合检验体系,并经实例检验,主要得出如下结论:
(1) 基坑变形受地质条件、施工阶段等因素的影响,具有明显的阶段性特征,因此,在基坑稳定性或变形规律研究中,有必要对其进行阶段性划分,以便分析不同阶段的稳定性或变形规律,且在实际施工过程中,可根据前期监测数据,对相应置信水平条件下的变形速率置信区间进行求解,以便检查奇异值,更好地指导现场监测工作。
(2) 基坑变形监测数据蕴含了基坑内部系统的力学演化信息,具有复杂性和非线性,因此,有必要合理结合多种方法来分析基坑的稳定性和变形趋势,这样可以增加分析结果的准确性和可信度。
(3) 尖点突变理论能准确判断基坑各工况条件下的稳定性,且通过Bartels检验能准确预测基坑稳定性的发展趋势;同时,波动互相关分析也能有效分析不同工况条件下的基坑变形发展趋势,且趋势分析结果与稳定性分析结果相符,验证了3种分析方法在基坑工程应用中的有效性。
