基于视觉敏感性的非对称建筑立面视觉均衡量化研究

霍海鹰，吕 典

1河北工程大学 建筑与艺术学院,河北 邯郸 056000 2邯郸市建筑物理环境与地域建筑保护技术重点实验室,河北 邯郸 056000 3中国建筑第五工程局华南分公司深圳分公司,广东 深圳 518000

0 引言

建筑外立面的设计不仅仅是设计师个性化的体现和实验性的产物,也应关注人们视觉生理的审美习惯来取得立面设计的视觉均衡效果.“造化赋形,肢体必双,神理为用,事不孤立”.对称事物自然是均衡的,但受实际条件制约,建筑立面在很多情形下采用非对称均衡设计,即利用不同体量、材质、色彩、虚实变化等平衡达到非对称均衡的目的[1].诸如巴西议会大厦、悉尼歌剧院、千禧教堂等一些视觉感受良好的非对称建筑立面能获得人们的普遍认可,其立面中是否存在某些客观的理性规律,值得深入探究.将审美的规律进行量化有助于其更好地进行传播和继承.

视觉敏感性是视觉系统对眼球感受事物所作出的应激反应,包括反应时间、反应准确程度等.其中，被观察物体的大小、方位、亮度、色彩等都会影响视觉敏感性[2].本文选取视觉敏感性中与建筑空间有关的属性进行研究,即物体的大小、方位,暂不考虑亮度、色彩等因素的影响，并针对在建筑立面构图中,视觉支点左右两边的视觉整体轮廓占比及其方位布局，对非对称建筑立面视觉均衡的影响进行研究.

国内外有关非对称建筑立面视觉均衡的研究,体现出以建筑科学与工程为核心,以视科学、心理学、计算机科学等学科为辅的学科交叉融合趋势.研究多侧重于立面虚实元素的占比、构筑物的尺寸比例等方面,同时结合问卷评价、美学实验等相关技术手段来对研究进行反馈验证.

Walter Niekamp[3](1981)发现人类的视知觉并不遵循几何光学规律,不同物体的相互位置关系对视觉重量有影响,即非线性视觉.

鲁道夫·阿恩海姆[4](Rudolf Arnheim,2006)基于人们在不对称构图中寻找视觉支点的这一天性,认为建筑立面的视觉均衡要通过建筑各部分或建筑与相邻建筑、景物间的协调比例达到，这时“支点”往往是入口、形象上的兴趣中心或图形上的重心.

杜异[5](2008)从灯光照明的角度出发,认为视觉敏感性是对某种视觉设计属性的权重,使视觉均衡中心两边的视觉趣味分量相当.

Zheng Bian等[6]人(2011)研究表明，视觉空间不是均匀的,随着视角变大,视觉会清晰——模糊——消失.

Jin-Ho Park[7](2018)通过沿街住宅立面的视觉敏感性“对称叠加”实验,认为错综复杂的不对称建筑立面也有实现视觉平衡的手段,即设计元素的分层权重叠加.

通过对前人研究的分析,总结非对称建筑立面的视觉均衡量化需要解决两方面问题:一是得到视觉敏感性在三维空间中的具体变化规律;二是利用这种变化规律对非对称立面进行视觉均衡的计算与评价.其基本流程为:确定建筑立面——设定观察视点——建筑立面整体轮廓识别——设定中心轴——中心轴两边设计元素的权重计算——视觉均衡感知.

1 量化模型的构建

建筑立面的形式丰富多样,不同观察点的立面视觉效果也有所差异,要实现其量化就有必要建立相应的视觉均衡量化模型,其中权重计算与视觉敏感性在三维空间中的变化规律密切相关,需设计实验得到实验数据进行拟合,得到视觉敏感性方程之后,从主立面的选取、视觉中心轴的定位和整体轮廓的提取三方面作为基础,对非对称建筑立面进行视觉均衡的量化计算.

参考詹姆斯·吉布森[8](James J.Gibson,1986)在《视知觉生态论》一书中的相关概念,本文将人对空间中某点的潜意识、快速的识别准确率定义为该点的视觉敏感性.人眼如同一台超高速帧照相机,视觉感知过程相当于视觉中心在若干个点之间来回扫描变换,二维信息到三维信息的转换受以往经验的影响[9].

在剥离材质、明暗等干扰因素情况下,微观上一定区域内的每个点视觉敏感性刺激值的累积值可代表区域对人视觉敏感性刺激总体影响,宏观体现在建筑上,即是对建筑轮廓内立面的总体感觉[10].

进行实际的主立面计算时,量化模型如下:若α为视点与被观察视点间的水平弧度,β为视点与被观察视点间的竖直弧度,定义空间某一点的视觉敏感性值为视点对该点的识别准确率Q=f(α,β).

以典型的矩形立面为例,在确定主立面、视中心轴线情况下,矩形区域映入眼里的面域的水平方向弧度范围为α∈[m1,m2],竖直方向弧度范围为β∈[n1,n2],则该立面区域对人敏感性总体感觉影响为：

将视觉中心轴左边立面轮廓的视觉敏感性刺激总影响值定义为S1,中心轴右边的定义为S2,则某视点的视觉均衡系数为：

VBC(Visual balance coefficient)=S小/S大

其中，S小取S1和S2中的较小值,S大取较大值,VBC越接近于1则建筑视觉均衡感越好,如图1所示.

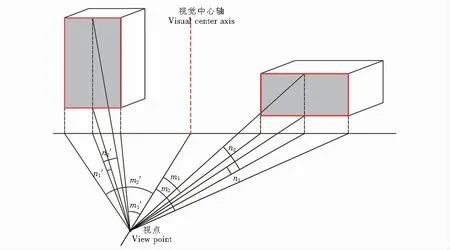
图1 典型矩形立面视觉均衡系数计算示意图Fig.1 Calculation of visual equilibrium coefficient of typical rectangular facade

2 视觉敏感性测量实验

为对建筑立面视觉均衡效果进行量化,

必须得到视觉敏感性在空间分布的特征与变化规律.从纯理论计算角度推导计算距离、角度与视觉敏感性之间的关系太过复杂,控制论学说体系为解决这类问题提供了一些思路,即将人们认识和改造的对象看作黑箱,主体输入可控制变量,观察客体输出的可观察变量[11].设计实验直接通过结果反推出最初参量间的关系是可行的手段,绕过了复杂的理论“黑箱”.实验前寻求计算机相关专业人员设计了视觉敏感性运行程序,该程序将某一尺寸的立面抽象成若干均匀排布的像素网格组成的平面,该平面会在随机位置的网格中随机闪烁某个字母,对网格中字母的识别率则可一定程度反映视点对网格中心点的视觉敏感性反应，然后在一定尺寸的电子大屏幕上同步笔记本运行的程序画面,实现对建筑立面识别的现实模拟.

图2 现场实验画面Fig.2 Field experiment screen

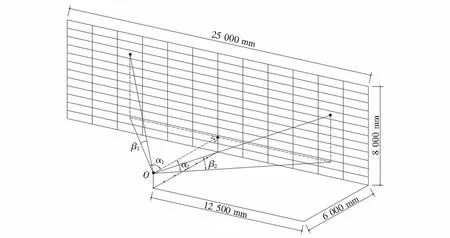
图3 现场实验观测简图Fig.3 Field experimental observation diagram

实验邀请40名(男女生各20人)河北工程大学在校生参加实验,年龄均在23～29岁之间,视力或矫正视力1.0左右.该实验在邯郸市规划展览馆沙盘模型厅进行,大屏幕尺寸为25 m*8 m.实验用1个可调节高度升降椅固定视点高度h(升降椅处于大屏幕竖直对称轴线上)、1个高度定位杆防止视点摇摆,2套数码分别录音和录像.实验参与人员在规划好的位置坐下后,大屏幕同步笔记本运行的程序画面.程序画面为一定规格的方格网,伴随每个方格内随机闪烁一个待识别的元素,参试人员对不同方位方格内元素的识别率一定程度反映其视敏度,现场实验如图2所示.视点定为O,默认视线的角度是眼睛与某个方格形心的夹角,如图3所示.

采集到的实验数据整理后,在1STOPT中采用非线性最小二乘法中的“麦夸特+通用全局优化算法(Levenberg-Marquardt+ Universal Global Optimization - UGO)”拟合曲线方程,对数据分析发现,d相当于变量α,β对Q影响很小,所以剔除d这一参数,得出Q=f(α,β).公式为:

式中,Q为被观察点相对于视点的视觉敏感性, %;α为视点与被观察点间的水平角度弧度值,rad;β为视点与被观察点间的竖直角度弧度值,rad.

图4 视觉敏感性与视角度三维曲面图Fig.4 Visual sensitivity and visual angle

在MATLAB中绘制出视觉敏感性Q随水平角度α、竖直角度β变换的空间三维曲面图,并与原数据进行对比,如图4所示.

3 部分经典案例选取计算

通过运用视觉均衡量化模型,对部分经典建筑设置观察点进行模拟量化分析,试图探索其立面设计中蕴含的视觉规律.所选的案例立面轮廓分明、立面材质简洁统一、视觉整体性强,有利于分析计算.实际案例分析时需结合周边环境、设计师意图等具体情况选定主立面和主要观察点区域,每个案例取5个观察点,中心轴正前方为基准观察点,并向左右两侧同等间距各取2点.模拟计算流程整理如表1所示.

表1 立面案例模拟计算Table1 Simulation calculation of elevation cases

模拟计算的相关数据整理如表2所示.

对表格数据进行分析和总结后发现,若立面两侧区域面积相差较大,观察点越靠近面积较小的一侧,视觉均衡效果越好;若立面两侧区域面积相差较小,观察点越靠近视觉中心轴,视觉均衡效果越好.

4 结论与总结

综合以上研究,总结非对称建筑立面的视觉均衡设计的量化手法，得出如下结论:

(1) 在非对称建筑立面设计中,若要取得视觉上的均衡,视觉中心轴两侧的整体轮廓到中心轴的距离应与面积成正相关,即轮廓面积越大离视觉中心轴应该越远,具体的尺度关系可由视觉均衡量化模型进行推算.

(2) 当视觉中心轴两侧立面区域面积相似时,为达到非对称均衡效果,可将一侧远离地平线,距离为d1,另一侧远离视觉中心轴,距离为d2.由视觉敏感性方程推算,d1与d2的比例约为0.76.

(3) 当视觉中心轴两侧立面区域面积相差较大时,视觉中心宜向立面区域面积较小的一侧偏移.若此时观测投影距离为d,立面区域较大一侧面积为L1*H,离视觉中心轴距离为d1,立面区域较小一侧面积为L2*H,离视觉中心轴距离为d2,则为达到立面上的视觉均衡应满足:

其中，f(α,β)的具体表达式见文中Q=f(α,β)公式.

非对称建筑立面视觉均衡量化模型能将立面视觉均衡审美转译为准确的数学图解,设计人员根据图解反映出的直观数据,结合自身经验、使用者需求、环境条件等因素进行循环反馈调节,能帮助设计师评价和优化非对称立面的设计.