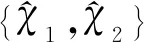含有2个非线性非忠实不可约特征标的有限群的若干性质
2020-12-16李亚利
李亚利,王 雪
(云南民族大学 数学与计算机科学学院 昆明 650031)
本文考虑的群都是有限群,提到的有限群的特征标总是指常特征标.符号Irr(G)表示群G的所有不可约特征标构成的集合, dl(G)表示群G的导长. 其它符号都是标准的,可以参阅文献[1].
设G为有限群, χ∈Irr(G),如果kerχ={g∈G|χ(g)=χ(1)}={1},则称特征标χ是群G的忠实不可约特征标.近年来,有限群的非线性非忠实不可约特征标性质对群结构的影响是一个重要的研究课题.文献[1]中定理12.5刻画了只含有0个非线性非忠实不可约特征标的有限群.2011年,Iranmanesh[2]探讨了只含有1个非线性非忠实不可约特征标的有限群的结构和性质,特别地,文献[2]中作者给出了只含有1个非线性非忠实不可约特征标的有限p-群的结构.2013年, Saeidi[3]研究了只含有1个非线性非忠实不可约特征标的可解群的性质和结构.2019年笔者分类了只含有2个非线性非忠实不可约特征标的有限p-群,具体的结论可以参看文献[4].
本文将讨论只含有2个非线性非忠实不可约特征标的任意有限群的性质,这些性质对后续考察这类群的结构有着重要的作用.
1 主要结论及其证明
任意有限群的所有不可约特征标核之交等于1,事实上,在文献[5]中,作者给出了结论:任意有限群的所有非线性不可约特征标核之交也等于1.下面我们将用不同与文献[5]中的方法,证明以下2种特殊情况.
引理1设有限群只含有1个非线性不可约特征标χ,则χ是忠实特征标.

于是,我们可以得到
也即 |K|·(|G′-1|)=|G′|-|G′∩K|,从而(|G′-1|)|(|G′|-|G′∩K|).又因为
|G′|-1≥(|G′|-|G′∩K|).
故得到|G′∩K|=1,于是G′∩K=1,这就迫使K=1,得到矛盾.矛盾说明只能成立K=1,因此χ是忠实特征标.
引理2设有限群只含有2个非线性不可约特征标χ1,χ2,则Kerχ1∩Kerχ2=1.

|G|-|G/G′|=χ1(1)2+χ2(1)2=|G/L|-|G/L∶(G/L)′| .
化简上面式子可以得到,|L|·(|G′-1|)=|G′|-|G′∩L|,从而(|G′-1|)|(|G′|-|G′∩L|),容易知道, |G′|-1≥|G′|-|G′∩L|,故得到|G′∩L|=1,于是G′∩L=1,从而L=1,得到矛盾.矛盾说明只能成立L=1,综上得征.
设G是有限群,如果χ∈Irr(G)且G/Kerχ只有唯一的极小正规子群,则称χ是群G的单基点特征标.下面稍偏离主题,给出有限群单基点特征标的核之交的1个结论.
命题1有限群G的所有单基点特征标的核之交是1.
证明记D是群G的所有单基点特征标的核之交,以及R是群G的任意1个极小正规子群.设M是G的最大的满足M∩R=1的正规子群,则可以断言RM/M是G/M的唯一极小正规子群.事实上,由于R是群G的极小正规子群,显然RM/M是G/M的极小正规子群.假设K/M是G/M的不等于RM/M的极小正规子群,则K是群G的极小正规子群且R∩K=1.注意到M 命题2设有限群G只含有2个非线性非忠实不可约特征标χ1,χ2.记Kerχi=Ki,i=1,2.则群G的不含G′的正规子群只有K1,K2,K1∩K2. 命题3设G为有限群,则下列结论成立. (i)如果群G只含有1个非线性非忠实不可约特征标χ,则群G的不含G′的非平凡正规子群只有Kerχ,且Kerχ是G的极小正规子群. (ii)如果群G只含有3个非线性非忠实不可约特征标χ1,χ2,χ3.记Kerχi=Ki,i=1,2,3.则群G的不含G′的非平凡正规子群属于集合{K1,K2,K3,K1∩K2,K1∩K3,K2∩K3,K1∩K2∩K3}. 命题3的证明参看文献[2]和[6]. 定理1设有限群G只含有2个非线性非忠实不可约特征标χ1,χ2.记Kerχi=Ki,i=1,2.且L=K1∩K2.则下列结论成立. (i)若L>1,则Z(G)为循环群,且K1/L,K2/L为G的主因子. (ii)若G′∩L≠1,则G′∩L为群G的唯一极小正规子群. (iii)若L>1且G′∩L=1,则L和G′为群G的全部极小正规子群以及G′∩K1=G′∩K2=1. 证明(i)由于L>1和引理2可得,群G必含有除χ1,χ2外的其它非线性不可约特征标.再结合群G满足的已知条件,可以知道这些除χ1,χ2外的非线性不可约特征标均是忠实的,因此Z(G)循环. 设群G的正规子群N满足L≤N≤K1,则G′⊄N,否则,若G′≤N,则G′≤K1,这与χ1为非线性特征标矛盾.由命题2可得N∈{K1,K2,L},故K1/L为群G的主因子.同理K2/L也为群G的主因子. (ii)设M为群G的任意非平凡正规子群.若G′≤M,则G′∩L≤G′≤M;若G′⊄M, 由命题2可得M∈{K1,K2,L},则G′∩L≤L≤M.总之无论何种情况,均有G′∩L≤M成立,从而群G′∩L为群G的唯一极小正规子群. (iii)因为G′∩L=1,所以L≤Ζ(G).设N为L的素数阶子群,则N是G的不含G′的正规子群,于是由命题2可得N=L.从而L为群G的素数阶极小正规子群.注意到G′∩L=1,结合命题2,可得G′和L是群G的全部极小正规子群.假设G′∩Ki≠1,i=1,2.由于G′∩Ki为群G的不含G′的正规子群且G′∩L=1,故由命题2必有G′∩Ki=L.于是L=G′∩Ki=G′∩Ki∩L=(G′∩L)∩Ki=1,i=1,2.这与已知条件L>1矛盾.从而成立G′∩K1=G′∩K2=1. 定理2(i)设有限群G只含有1个非线性非忠实不可约特征标χ,则当G非可解时, ∀r≥2,G(r)=G′.当G可解时,G的导长dl(G)≤3. (ii) 设有限群G只含有2个非线性非忠实不可约特征标χ1,χ2,记Kerχi=Ki,i=1,2.且L=K1∩K2.则当G非可解时, ∀r≥2,G(r)=G′.当G可解时,G的导长dl(G)≤4. 证明(i)考虑G的换位子群G″,若G″=G′,则显然∀r≥2,G(r)=G′成立.以下假设G是可解群,则G″ (ii)由于G的换位子群G″≤G′,同上当G″=G′,则∀r≥2,G(r)=G′成立.下面设G可解.若1