基于改进EKF的柔性绳索自动升降装置姿态估计

张富春，郑武略，汪 豪，吴阳阳，丁红涛，崔家山

(1.中国南方电网超高压输电公司广州局， 广州 510405; 2.西安电子科技大学空间科学与技术学院， 西安 710126)

高空检修作业是电网稳定运行的必要手段。近年来，新建线路均采用高跨设计，而且大部分线路地处偏远、环境恶劣、交通不便，这对线路高空维护检修及其安全性带来了巨大挑战。目前，国内外科研人员针对高空作业安全与防坠进行了深入研究与探索，并取得了一系列成果[1-3]，但绝大多数方案是基于机械原理实现的，即通过结构设计，增加系统的摩檫力。

在其他行业出现了通过MES(Microelectro Mechanical Systems)传感器检测装置姿态的方式进行安全性研究[4-6]。在导航与制导领域，出现了井喷的现象。文献[7]提出了基于互补滤波器的姿态信息融合方法。文献[8]设计了基于梯度下降法的互补滤波器进行四元数误差估计，并应用于开源无人机项目。国内外学者对基于惯导系统加上磁力计的互补滤波算法进行了大量研究[9-10]，后来Premerlani W和Bizaed P对Mahony的互补滤波算法进行了验证，并形成了开源飞控APM和PX4的姿态解算互补滤波算法[11]。扩展卡尔曼滤波算法作为非线性系统下的高效算法也被大量的应用于飞行器的姿态解算中[12-14]。

基于已有检测方法，针对输电线路高空作业特点，研究了基于改进扩展卡尔曼滤波的柔性绳索自动升降装置姿态估计方法。

1 姿态表示方法

姿态用于描述刚体的刚体坐标系和参考坐标系之间的角度位置关系，如图1所示。

图1 姿态表示的角度位置关系

常见的表示方法有方向余弦矩阵、欧拉角和四元数。柔性绳索自动升降装置的姿态信号指的是柔性绳索自动升降装置在导航坐标系下的空间位置信息表示，即机体坐标系在导航坐标系中的方位，考虑到处理的方便性，采用四元数表示[15]。定义四元数q为：

(1)

为了简化描述，四元数q可以写为：

(2)

式(2)中，q0,…,q3称作旋转四元数。

定义υB和υN分别表示机体坐标系和导航坐标系中的矢量，则有：

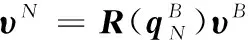
(3)

(4)

为了书写简便，旋转矩阵可以简写为：

(5)

与此同时，姿态四元数也可以由旋转矩阵表示为：

(6)

四元数q的时间变化率与柔性绳索自动升降装置的运动角速度ω之间的关系可由如下的动力学方程表示：

(7)

式(7)中：ω表示陀螺仪的输出

(8)

Ω(ω)和Ξ(q)分别由角速度和四元数组成

(9)

(10)

式(9)、式(10)中：I表示单位阵；反对称矩阵运算符⎣qv×」定义为

(11)

姿态检测传感器中，一般将陀螺仪和加速度计作为核心器件，而磁力计仅对陀螺仪在偏航角上的积分进行长时矫正[16]。

加速度计测量的是重力分量，当检测变速运动的加速度信号时，会导致姿态角的解算不准确。陀螺仪测量升降装置角速度时，随着积分时间的增加，其误差增加。磁力计测量地磁场强度在升降装置倾斜时，其计算结果也需要根据倾斜角进行补偿。因此，需对多种传感器进行数据融合，解算出更准确的姿态。

2 基于四元数的扩展卡尔曼滤波

扩展卡尔曼滤波 (extended kalman filter， EKF)是一种应用最广泛的非线性滤波方法。EKF采用围绕上一步估计值Xk将非线性函数f(·)和h(·)展开成泰勒级数，并取一阶近似来进行线性化，再利用滤波递推方程进行系统的状态估计。当系统具有较强的非线性或初始误差较大时，滤波精度明显下降，甚至造成滤波发散[17]。

EKF用于处理非线性离散时间过程，其同样使用两步法：预测-校正进行状态估计。预测过程根据当前时刻的系统状态获得下一时刻的先验估计；校正过程将观测和先验估计相结合获得改进的系统后验估计。

2.1 离散化

与其他典型非线性系统相同，柔性绳索自动升降装置的系统状态方程也可以表示为：

(12)

式(12)中:f(·)为多维向量函数，并且相对于其独立变量都是非线性的；h(·)是一个非线性向量函数；W(t)和V(t)分别表示过程噪声和观测噪声。

EKF算法中一个关键的部分就是状态方程与观测方程从非线性转化为线性，最终变成一个离散的系统。为了使状态变量成为线性的，可以将X(t+Δt)在X(t)处进行泰勒展开，考虑到实际情况，这里仅取二阶近似值，有：

(13)

式(13)中：

忽略高阶项，系统状态方程的离散形式可以表示成如下的标准状态空间形式，即：

(14)

这里假定W(k)和V(k)都是均值为0的高斯白噪声，方差分别记作Qk、Rk。A(X(k))表述为：

(15)

2.2 建立系统过程方程

由于MEMS陀螺仪存在静态漂移，故将姿态四元数和陀螺仪偏差作为EKF的状态变量，记作：

(16)

柔性绳索自动升降装置通常是由三轴陀螺仪来测量旋转角速度，众所周知的是，陀螺仪非常容易受到角速度噪声以及温度等的影响。本文采用如下的陀螺仪模型(这是Farrenkopf 在1974年提出的既简单又实用陀螺模型[18])：

(17)

(18)

陀螺仪的角速度偏移也并非静态常量，其表现为二阶高斯白噪声，表示为：

(19)

式(19)中：

根据式(7)和式(19)，可以得到柔性绳索自动升降装置状态方程的微分形式为：

(20)

在预测过程中，使用式(20)的简化形式：

(21)

由于采样时间非常短，在积分过程中认为陀螺仪偏移量为常值，可以得到：

(22)

并且

(23)

最终建立系统的状态方程为：

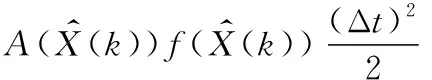
(24)

2.3 建立离散测量方程

为了使状态向量的测量更直观，即使测量矩阵更简单，本文选择姿态四元数作为测量变量。因此测量向量为：

(25)

使用高斯牛顿算法[19]、或者求解Wahaba问题[20]，可以直接根据加速度计与磁力计的输出计算出机体的四元数。但是由于地磁常量难以确定并且极易受到周围铁磁体的干扰，本文提出了一种向量正交化的方法，使用加速度计与磁力计的的测量值得到单位正交的旋转矩阵，进而计算出机体的单位四元数。旋转矩阵由三维向量i,j,k组成，分别代表机体的X,Y,Z三个体轴向量。因此有：

(26)

(27)

加速度计的输出用于构造机体坐标系的Z轴，将X轴强制与Z轴垂直，可以计算出i为：

(28)

由于选择矩阵为单位正交矩阵，可以直接将k和i叉乘得到向量j为：

(29)

(30)

由此可得四元数的测量值为：

(31)

2.4 EKF的实现

EKF滤波算法的工作原理如图2所示。

图2 扩展卡尔曼滤波算法的工作原理框图

根据式(24)和式(31)推导出的状态向量和测量向量表达式以及EKF工作原理，可得基于四元数的扩展卡尔曼滤波器的五步法：

步骤1：估计先验状态。

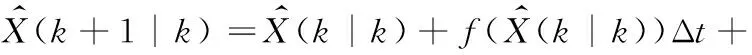
(32)

步骤2：计算先验误差协方差矩阵。

P(k+1|k)=Φ(k)P(k|k)ΦT(k)+Qk

(33)

式(33)中：

Q(k)=E[W(k),W(k)T]

(34)

步骤3：计算卡尔曼增益。

K(k+1)=P(k+1|k)HT(k+1)×

(35)

式(35)中：

(36)

步骤4：估计后验状态。

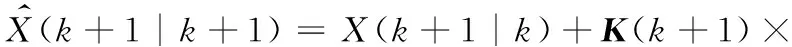
{Z(k+1)-h[X(k+1|k)]}

(37)

步骤5：计算后验误差协方差矩阵。

P(k+1|k+1)=[I-K(k+1)H(k+1)]P(k+1|k)

(38)

3 仿真实验

为了验证上述算法的有效性，分别对升降装置在静态和动态下的传感器原始数据进行了实验。数据采样频率50 Hz。为了获得升降装置的参考位姿，使用二维转台的数据作为参考，其旋转精度可达到0.1°。二维转台和升降装置姿态检测传感器模块如图3所示。

图3 二维转台及升降装置姿态检测传感器

3.1 静态测试

首先，将升降装置姿态检测传感器模块静止放置在二维转台上，设置系统的采集频率为100 Hz，采样个数5 000点。加速度计和陀螺仪原始数据分别如图4、图5所示。

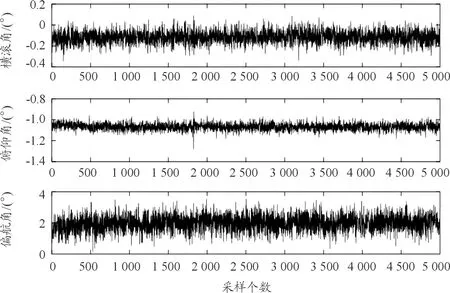
图4 静态加速度计测量数据曲线

图5 静态陀螺仪测量数据曲线

对数据进行分析后，得到横滚角的样本方差为0.003 24，俯仰角的样本方差为0.000 991 3，偏航角的方差为0.241 37。

对数据进行分析后，得到横滚角的样本方差为3.068 26×10-7，俯仰角的样本方差为2.535 02×10-7，偏航角的方差为9.759 27×10-7。

然后，将升降装置载重250 kg悬置在半空中进行了悬停测试，悬置方向以普通的指南针为参考，升降装置悬停测试如图6所示。

图6 升降装置悬停测试

传感器原始数据和姿态输出信息分别如图7～图10所示。

图7 加速度计数据曲线

图8 磁力计数据曲线

图9 陀螺仪数据曲线

图10 姿态角输出数据曲线

由图7-图9可以看出：传感器在悬停状态下的输出与静止状态基本一致，但数据的动态范围要大于静止状态，其原因在于，悬停状态的升降装置受吊绳垂直与水平方向的弹性形变影响，存在微振动现象。经过滤波之后，由图10可以看出：横滚角、俯仰角和偏航角的偏差基本上控制在0.2°之内，较为真实准确的反应了升降装置在悬停状态下的姿态信息。同时采用了陀螺仪误差的四元数状态能够通过扩展卡尔曼滤波有效的修正陀螺仪零点漂移带来的累计误差。

3.2 动态测试

设置转台分别在X轴和Y轴进行±2°和0～25°匀速旋转，传感器数据进行采集，并分别使用本文所提方法与梯度下降法、高斯牛顿算法GDA和未改进EKF以及两轴转台所测得的数据进行对比，结果如图11所示。

从图11中显示的效果看来，这3种算法都能够有效地进行姿态估计。但本文所提算法在保持平滑前提下收敛速度也快于其他的EKF算法。

图11 动态测试姿态角输出数据

4 结论

提出了一种柔性绳索自动升降装置姿态估计算法，使用姿态四元数表示柔性绳索自动升降装置的姿态，并使用扩展卡尔曼滤波器(EKF)进行数据融合。静态实验和动态实验验证了所提方法的有效性，静态偏差控制在0.2°之内，且在保持平滑的前提下收敛速度快于传统EKF算法。为研制基于姿态估计的柔性绳索自动升降装置安全防坠系统提供了数据支撑。