雷达天线伺服系统误差分析

余 驰，杨 超，张钢峰

(庆安集团有限公司 航空设备研究所， 西安 710077)

雷达系统对目标的探测和识别，在精确制导技术、反隐身技术、光电对抗技术和C5I(指挥、通讯、计算、控制、对抗和情报)中起到重要的作用。它为信息的获取与态势感知、进行指挥决策和评估分析提供了依据。它的总体技术指标和性能与收发光学子系统、信号处理子系统、伺服控制子系统密切相关[1]。雷达天线伺服系统是实现雷达天线快速响应、大范围伺服和空间精确定位定向的伺服控制系统。它是雷达系统进行快速准确跟踪和定位的前提[2]。已经被广泛应用在陆海空等领域中[3]，它随着伺服控制技术、电机及驱动技术、传感器技术、精密传动技术和振噪控制技术的发展，不断的向大范围随动、高精度控制、快速伺服响应的方向发展。雷达天线伺服系统按照一定的速度、范围、扫描算法驱动天线对一定空域进行周期性的扫描、探测，以进行外部环境感知和目标信息获取。而在实际应用中，因为雷达天线伺服系统加工精度、装配配合、轴承间隙、载荷分布引起的变形等因素的综合作用，将影响雷达天线伺服系统的动态精度和定向精度，给探测目标的精度、态势评估和判断决策带来负面影响。文献[4-6]对雷达天线伺服系统的控制器、运动控制补偿算法、抗干扰控制技术进行了建模仿真与研究。文献[7-9]对雷达天线跟踪方式、伺馈训练关键技术、基于模型的雷达天线伺服系统设计进行分析和研究。文献[10-15]对雷达天线的安装调整和调平、检测精度方法、挂装姿态标定、扫描噪声、天线伺服动力学和雷达天线驱动进行了研究。而雷达天线伺服系统的误差控制、分配综合是提高精度的有效措施之一。

本文以雷达天线伺服系统两自由度伺服运动为基础，建立了伺服系统的误差数学模型，并对误差源进行了分析。通过对误差在不同伺服位置的精度影响特性的研究，可用于雷达天线伺服系统的精度分配、轴系综合误差控制和评估分析。

1 坐标系建立与误差数学模型分析

以雷达天线伺服系统两自由度伺服运动的轴线建立如图1所示坐标关系，Yf为方位自由度，Pf为俯仰自由度，以实现在方位和俯仰2个自由度的伺服运动。建立载体坐标系OXaYaZa、雷达天线伺服系统方位自由度坐标系OXyYyZy和俯仰自由度坐标系OXpYpZp。φ、ψ分别为方位自由度坐标系OXyYyZy和俯仰自由度坐标系OXpYpZp绕OZa和OXy旋转的方位角和俯仰角。

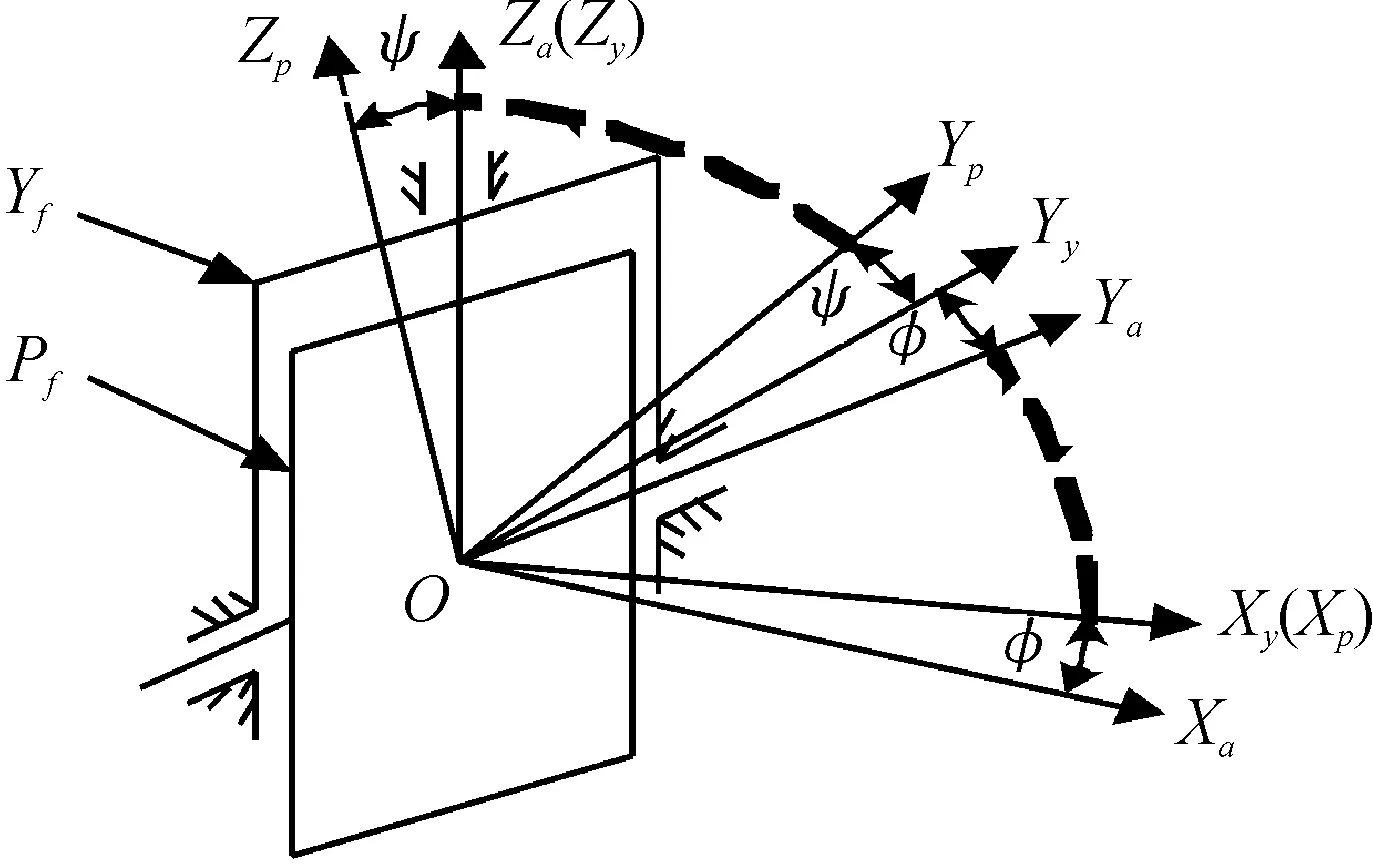
图1 雷达天线伺服系统坐标关系图

设A是OXaYaZa坐标系中有一个向量，则该向量在OXaYaZa坐标系中三个轴的分量分别为Aax、Aay、Aaz。在理想状态时，Aax、Aay、Aaz通过OZa轴的摩擦传递和几何约束耦合到方位自由度中，如图2所示，可以得到Aax、Aay、Aaz在方位自由度坐标系OXyYyZy三个轴的分量分别为Ayx、Ayy、Ayz。即：

(1)

图2 方位与载体坐标系的关系图

其中：

(2)

Ayx、Ayy、Ayz通过OXp轴的摩擦传递和几何约束耦合到俯仰自由度中，如图3所示，可以得到Ayx、Ayy、Ayz在俯仰自由度坐标系OXpYpZp三个轴的分量分别为Apx、Apy、Apz。即：

(3)

图3 俯仰与方位坐标系的关系图

其中：

(4)

Tp,a=Tp,yTy,a

(5)

(6)

在考虑轴系综合误差时，设α为方位自由度轴系误差角度，β为俯仰自由度轴系误差角度。如图4所示，因为综合轴系误差的存在等效于OXaYaZa坐标系绕OZa和OXa1旋转了一个α和β的旋转角，OXaYaZa坐标系绕OZa旋转α形成了OXa1Ya1Za1坐标系，OXa1Ya1Za1坐标系绕OXa1旋转β形成了OXa2Ya2Za2坐标系。则A向量在OXaYaZa坐标系中3个轴的分量分别为Aax、Aay、Aaz在OXa1Ya1Za1坐标系和OXa2Ya2Za2坐标系的分量分别为Aax1、Aay1、Aaz1和Aax2、Aay2、Aaz2。

图4 雷达天线伺服系统轴系综合误差坐标关系图

其中：

Aax1、Aay1、Aaz1通过OXa1轴选转β，可以得到Aax1、Aay1、Aaz1在OXa2Ya2Za2坐标系3个轴的分量分别为Apx2、Apy2、Apz2。即：

其中：

(7)

因为轴系综合误差α和β的存在，在OXaYaZa坐标系中的A向量，分解到OXa2Ya2Za2坐标系中三个轴的分量变为Aax2、Aay2、Aaz2。如图5所示，当方位自由度坐标系OXyYyZy和俯仰自由度坐标系OXpYpZp绕OZa2和OXy旋转的方位角和俯仰角分别为φ、ψ时，Aax2、Aay2、Aaz2变化为Apxe、Apye、Apze，即表示为OXaYaZa坐标系中的向量A，因轴系综合误差α和β的存在，同样经过方位角φ和俯仰角ψ时变换为Apxe、Apye、Apze。根据式(1)～式(6)可以得：

图5 轴系综合误差伺服运动状态关系图

整理后可得：

cosφcosψsinαsinβ+sinψsinαsinβ，sinφsinψcosα+

cosφsinψsinβcosβ+cosψsinαsinβ,cosφsinα+sinφcosαcosβ，

-sinφcosψsinα+cosφcosψcosαcosβ-sinψcosαsinβ，

sinφsinψsinα-cosφsinψcosαcosβ-cosψcosαsinβ，

sinφsinβcosφcosψsinβ+sinψcosβ-cosφsinψsinβ+cosψcosβ]

在OXaYaZa坐标系中的向量A，即Aax、Aay、Aaz在理想状态和有轴系综合误差时引起的运动误差值为：

(8)

在OXaYaZa坐标系中的向量A，分解到OXaYaZa坐标系中3个轴的分量 为Aax、Aay、Aaz。雷达天线伺服系统的轴线一般与OYa重合或平行，为了简化分析取与OYa重合，并将向量A单位化，则有：

(9)

联立式(6)、式(7)、式(8)和式(9)后整理可得：

(10)

2 雷达天线伺服系统误差源的分析

雷达天线伺服系统主要是为雷达天线的稳定和精确伺服运行提供保障，其动态精度和轴向定向精度将直接影响探测目标的精度、态势评估和判断决策。因此，需要根据要求对误差进行控制、分配与综合。实际应用中雷达天线伺服系统因加工精度、装配配合、轴承间隙、载荷分布引起的变形等因素的综合作用，误差是必然存在的。其误差主要有方位伺服轴系综合误差和俯仰伺服轴系综合误差。

2.1 方位轴系综合误差分析

1) 方位轴与方位伺服框架垂直度引起的误差。方位轴与方位伺服框架之间可能是一体加工结构或有安装配合，因加工精度，必然存在垂直度误差，设垂直度引起的误差为δy1，Δy1为垂直度，Ly1为方位轴支撑轴承之间的距离，则有：

δy1=atan(Δy1/Ly1)

(11)

2) 轴承径向跳动及间隙误差。方位轴通过轴承支撑于基础结构上，设ED1为轴承径向跳动量，Δy2为轴承径向间隙。假设跳动引起的误差与间隙误差相互独立，误差合成后总误差为σy1，设轴承径向跳动及间隙引起的误差为δy2，则有：

(12)

δy2=tan-1(σy1/Ly1)

(13)

3) 方位轴安装偏心误差。方位轴的同轴度误差Δy3和圆度误差Δy4，安装孔的圆柱度误差Δy5，假设各个误差相互独立，按照误差合成后总误差为σy2，设方位轴安装偏心引起的误差为δy3，则有：

(14)

δy2=atan(σy2/Ly1)

(15)

4) 方位轴变形引起的误差。方位轴通过支撑轴承安装与载体结构上，方位轴上有方位框，俯仰框通过机械安装于方位框。设方位轴承载的所有结构总重量为Gy1，重心偏离方位轴的偏心距为ey1，重心距离方位轴伺服支撑距离为Ly2，Ey为方位轴材料的弹性模量，Iy为方位轴薄弱截面的惯性矩，则方位轴变形引起的误差δy4为

δy4=Gy1ey1Ly2/EyIy)

(16)

5) 方位轴系综合误差合成。因方位轴与方位伺服框架垂直度引起的误差δy1、轴承径向跳动及间隙误差δy2、方位轴安装偏心误差δy3和方位轴变形引起的误差δy4的存在，多个误差因素，其具有一定的随机性，且相互独立或弱相关，按照误差合成的理论采用均方根法来进行分析，方位轴系综合误差为设δy。则有：

(17)

2.2 俯仰轴系综合误差分析

1) 俯仰轴与俯仰伺服框架垂直度引起的误差。俯仰轴与俯仰伺服框架之间可能是一体加工结构或有安装配合，因加工精度，必然存在垂直度误差，设垂直度引起的误差为δp1，Δp1为垂直度，Lp1为俯仰轴支撑轴承之间的距离，则有：

δp1=atan(Δp1/Lp1)

(18)

2) 轴承径向跳动及间隙误差。俯仰轴通过轴承支撑于基础结构上，设轴承径向跳动量为ED2，轴承径向间隙为Δp2，假设跳动引起的误差与间隙误差相互独立，误差合成后总误差为σp1，设轴承径向跳动及间隙引起的误差为δp2，则有：

(19)

δp2=atan(σp1/Lp1)

(20)

3) 俯仰轴安装偏心误差。方位轴的同轴度误差Δp3和圆度误差Δp4，安装孔的圆柱度误差Δp5，假设各个误差相互独立，按照误差合成后总误差为σp2，设方位轴安装偏心引起的误差为δp3，则有：

(21)

δp3=atan(σp2/Lp1)

(22)

4) 俯仰轴变形引起的误差。俯仰轴通过支撑轴承安装与方位框，设俯仰轴的跨距为Lp2，俯仰轴上的总重量为Gp1，重心与俯仰轴的中心偏离量为ep1，Ep为俯仰轴材料的弹性模量，Ip为俯仰轴薄弱截面的惯性矩，则俯仰轴变形引起的误差δp为

(23)

其中δp40和δp41分别为俯仰轴支撑两端的误差：

(24)

(25)

5) 俯仰轴系综合误差合成。因俯仰轴与俯仰伺服框架垂直度引起的误差δp1、轴承径向跳动及间隙误差δp2、俯仰轴安装偏心误差δp3和俯仰轴变形引起的误差δp4的存在，多个误差因素，其具有一定的随机性，且相互独立或弱相关，按照误差合成的理论采用均方根法来进行分析，方位轴系综合误差为设δp。则有：

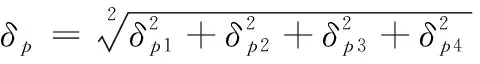
(26)

2.3 轴系综合误差合成与分析

设δ为总的轴系综合误差，按照δy和δp相互独立，则有：

(27)

雷达天线伺服系统通过方位和俯仰伺服运动实现对一定空域范围的扫描。由式(21)到式(27)的分析可知，因加工精度、配合、轴系在结构间的跨度、变形等多种因素影响和制约，同时考虑到载荷、过载的应用需求，误差一般需要控制在10′以内。根据以上的基本分析，可对1′、5′、10′误差下的系统按照建立的数学模型进行仿真与分析。

3 仿真与结果分析

3.1 仿真试验

依据第二节的模型与分析可知，由于诸多误差因素的必然存在，折合到输出轴不可避免会产生雷达天线伺服系统在方位轴和俯仰轴的轴系误差。当雷达天线伺服系统轴系在方位轴和俯仰轴的误差角度分别为α、β时，为了扫描探测空间一定范围的某目标或监控某区域时，设雷达天线伺服系统需要伺服运动的方位和俯仰角度分别为φ、ψ，将式(10)中ΔApx和ΔApz线位移误差转换为对应的角位移误差，按照表1给出了3组误差参数算例，可以得出不同轴系综合误差情况下在方位、俯仰和两自由度伺服合成的误差仿真试验曲线，见图6～图14。

表1 伺服运动角度和轴系误差参数

图7 俯仰轴系误差曲线Ⅰ

图8 2个自由度合成的轴系误差曲线Ⅰ

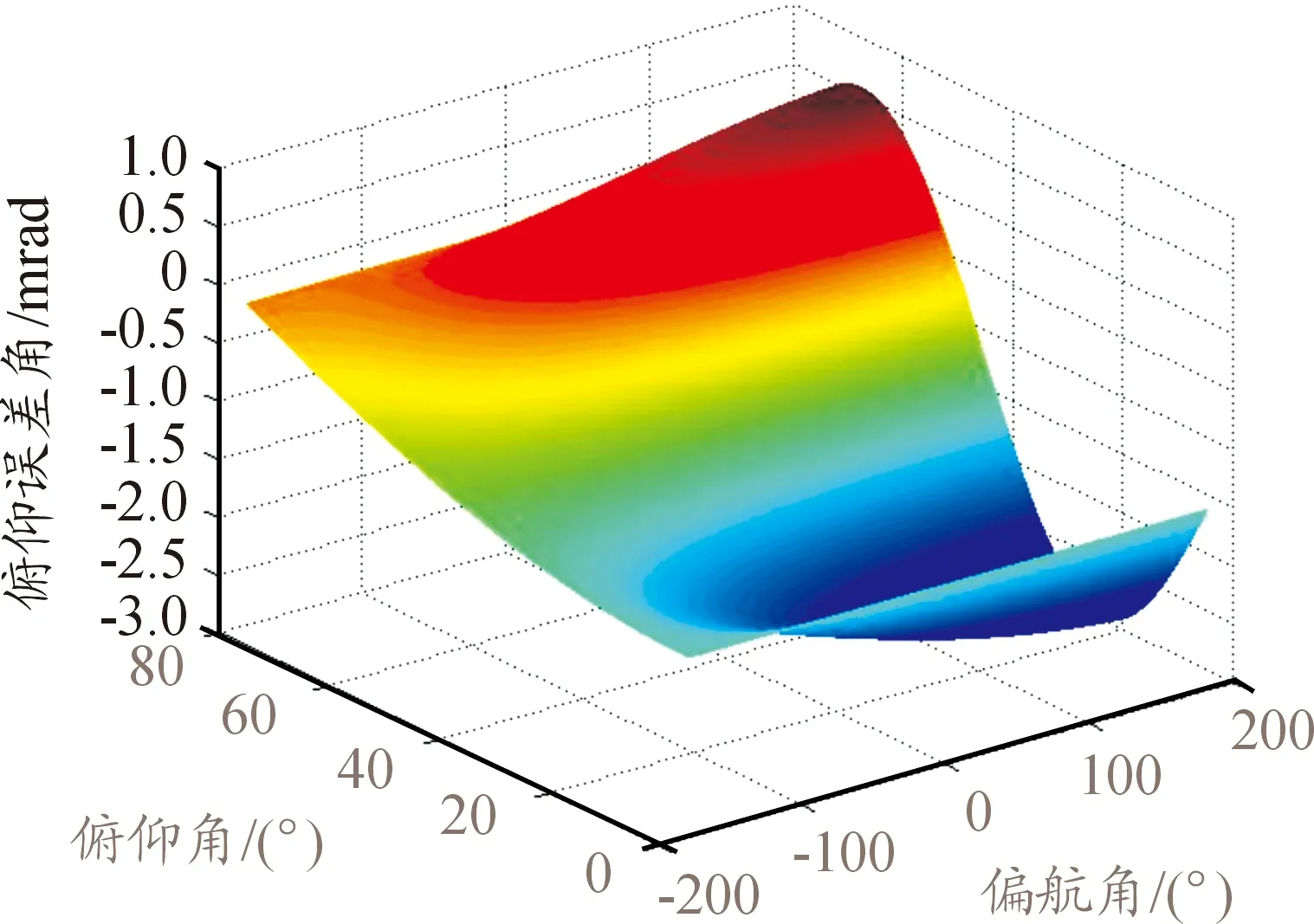
图9 方位轴系误差曲线Ⅱ

图10 俯仰轴系误差曲线Ⅱ

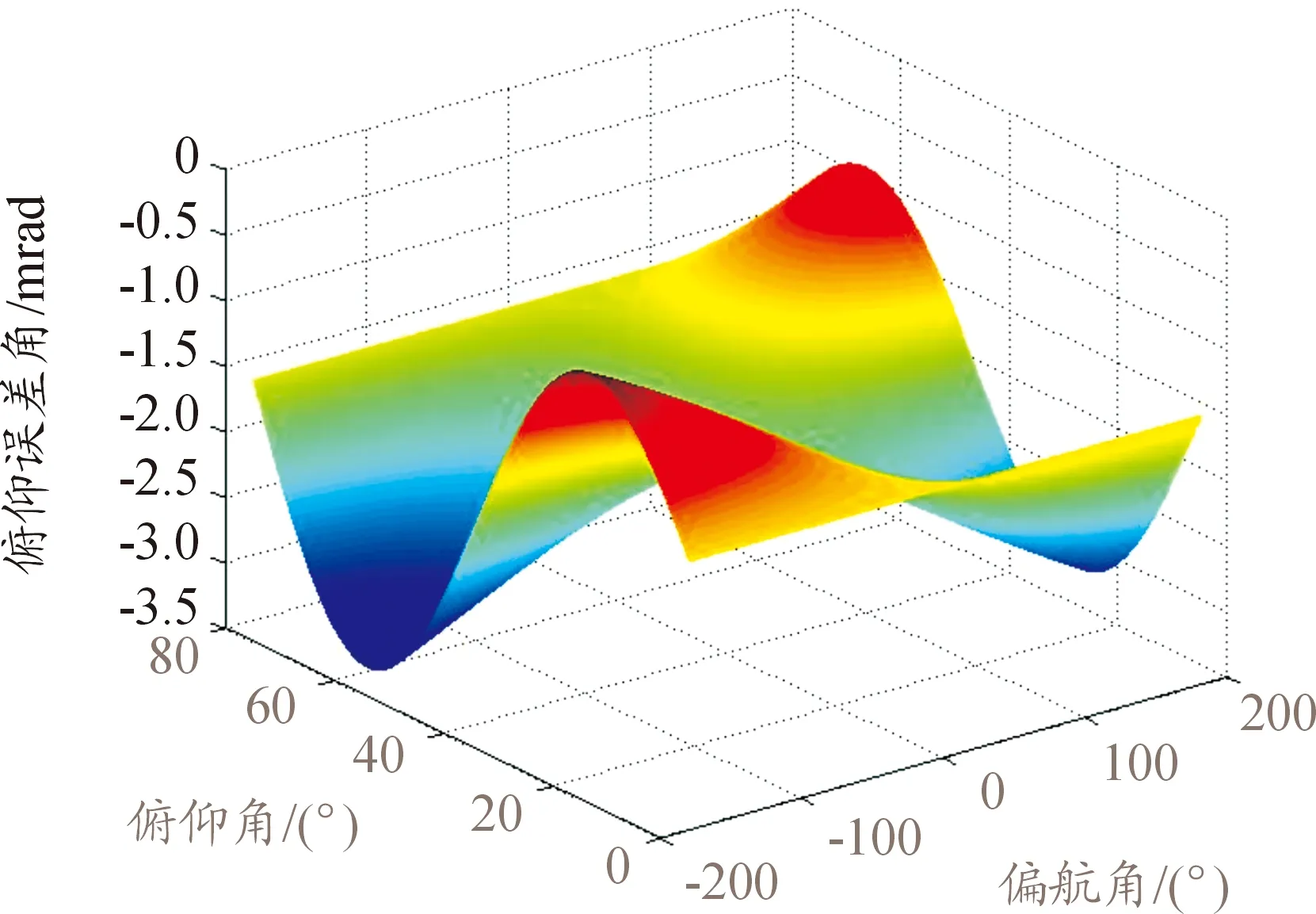
图11 2个自由度合成的轴系误差曲线Ⅱ

图12 方位轴系误差曲线Ⅲ

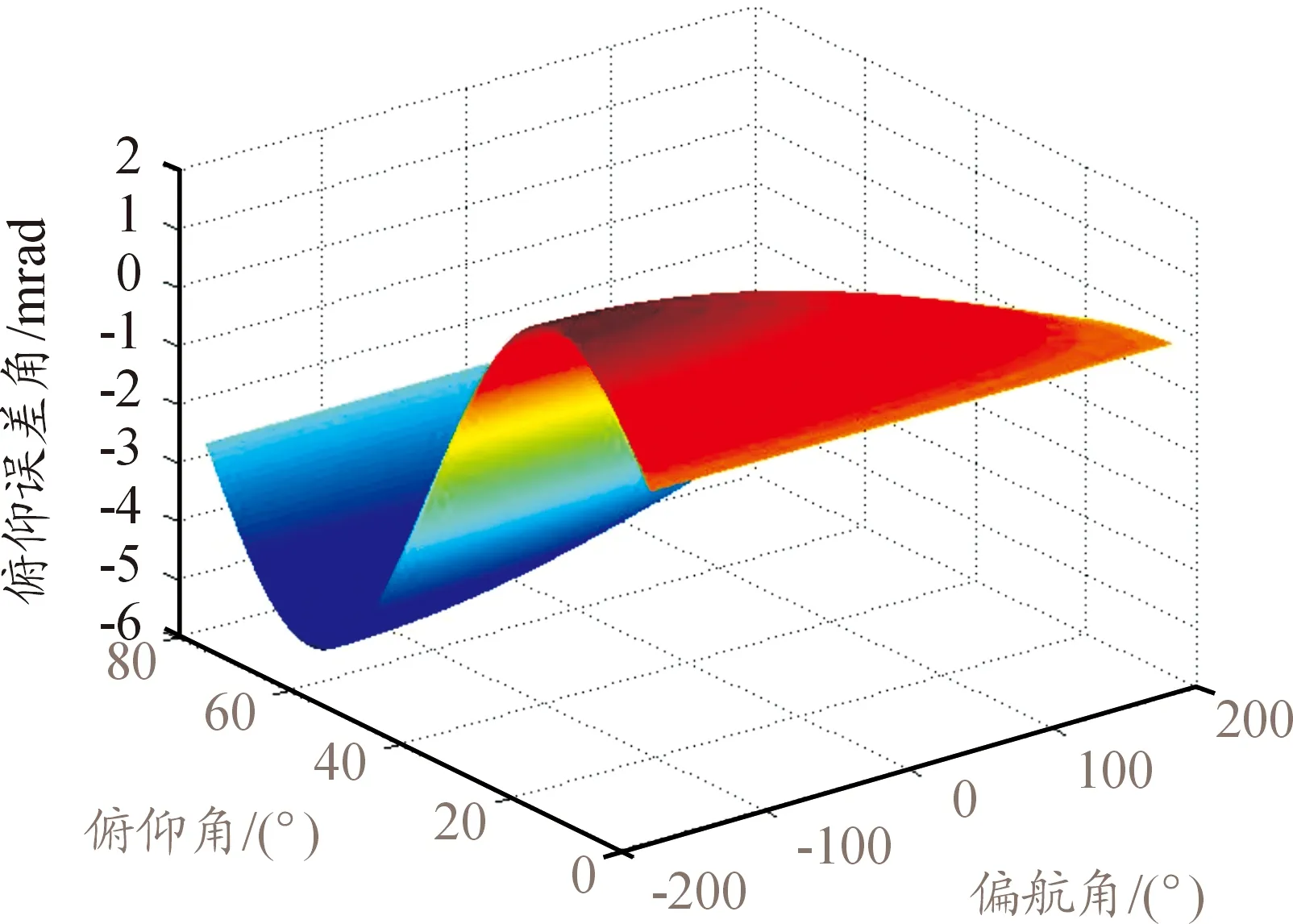
图13 俯仰轴系误差曲线Ⅲ

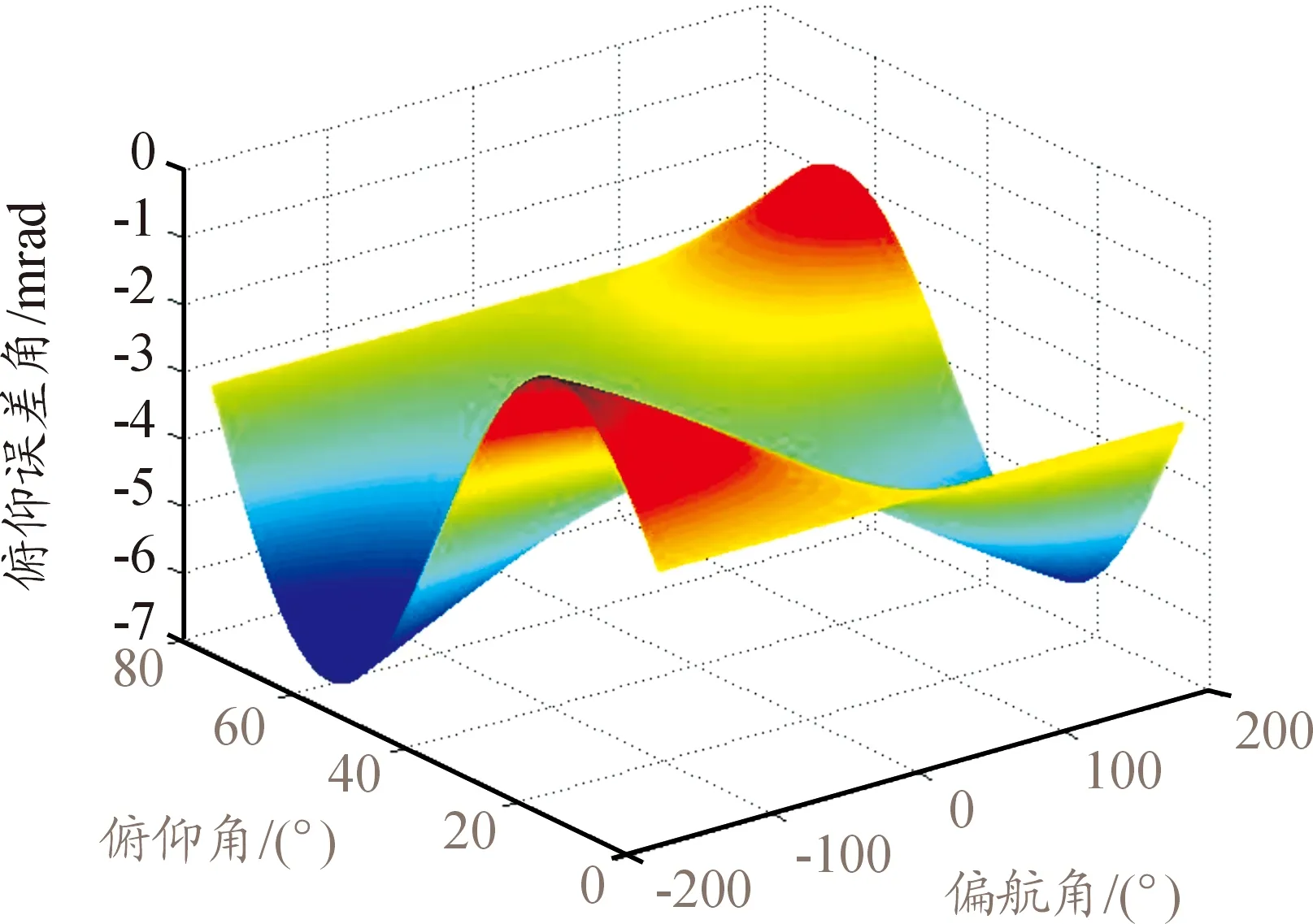
图14 2个自由度合成的轴系误差曲线Ⅲ

3.2 结果分析

当存在1′、5′和10′的方位轴和俯仰轴综合误差时，在不同的方位和俯仰伺服运动角度跟踪下。图6、图9和图12仿真试验曲线可知，方位轴系误差在方位角和俯仰角[180,20]时，分别达到最大值为-0.55 mrad、-2.8 mrad和-5.5 mrad。由图7、图10和图13仿真试验曲线可知，俯仰轴系误差在方位角和俯仰角[-180,60]时，分别达到最大值为-0.53 mrad、-2.6 mrad和-5.2 mrad。通过图8、图11和图14仿真试验曲线可知，2个自由度伺服运动合成后，合成误差在[-180,60]时，分别达到最大值为-0.68 mrad、-3.4 mrad和-6.8 mrad。上述的分析表明，在不同伺服运动位置和精度要求的雷达天线伺服系统中，轴系综合误差的存在，将对不同伺服跟踪位置目标探测时产生不同的精度影响。因此在雷达天线伺服系统设计时，需要根据伺服运动范围和实际精度使用的要求，按照建立的数学模型、进行误差源分析和仿真试验，并根据结果进行精度分配、轴系综合误差控制和评估分析。

实际应用中雷达天线伺服系统因加工精度、装配误差、成件精度和变形引起的误差等因素的综合作用，误差是客观存在的。这些误差将通过结构几何关系耦合到方位轴和俯仰轴，即会产生相应的轴系综合误差。因此需要对误差产生的影响进行有效的控制、补偿和消除。以提高雷达天线伺服系统的运动精度。

4 结论

在建立雷达天线伺服系统运动误差数学模型的基础上，通过误差源的分析，对不同误差对伺服运动精度的影响进行了仿真试验与分析，可为雷达天线伺服系统精度控制、分配与综合提供设计参考。