军用多轮电驱动车辆稳定性及转矩分配控制

马晓军，王科淯，刘春光，张 征

(中国人民解放军陆军装甲兵学院 兵器与控制系， 北京 100072)

军用多轮电驱动车辆作为战场人员装备输送平台，需要具备较高的越野能力，在复杂路面仍能保持较好的稳定性、机动性；同时为了持续作战和远距离运输，也需具备较好的续航能力，所以能耗经济性也是车辆行驶控制的重点优化方面之一。

针对类似车辆的行驶控制问题，近年来主流控制方法之一为直接横摆力矩控制，通过同时控制横摆角速度和质心侧偏角2个变量，给出维持车辆稳定行驶所需整车横摆力矩目标值并分配至各车轮[1-2]。这一类控制策略中主要存在2个问题：一是上层控制器需要协调控制2个变量，而二者的控制过程存在矛盾，有学者将控制范围分区，在不同的区域控制不同的变量，以减弱控制过程中的矛盾，也有学者尝试分别对2个变量进行跟踪控制，之后综合两部分控制结果[3-4]，针对军用运载车辆的较为成熟的相关研究及应用仍然较少；二是从整车到各轮的转矩分配问题，民用越野车、工程车及军用车辆的相关研究设计中，多以轮胎附着裕度为优化目标设计转矩分配方案[5]，而城市民用车辆领域，优化目标多围绕能耗经济性展开设计[6-7]。总体而言，多数控制策略优化目标较单一，不能很好地适用于军用运载车辆的行驶控制问题。

本文设计了一种分层控制器，上层控制首先针对两变量分别实现单独控制，其次设计动态加权函数，通过加权求和，削弱多变量控制矛盾，实现两变量的协调控制，得出上层输出。在下层控制中，结合军用多轮运载车辆的运用特点，设计了一种针对复合目标的转矩优化分配方案，综合考虑轮胎附着裕度优化和能耗经济性优化，优先考虑上层控制目标在下层的实现问题，其次当情况允许时，通过转矩优化分配提高能耗经济性。最后在人在环仿真试验平台进行典型工况试验，验证控制方法的有效性，为类别相似车辆的行驶控制策略制定提供参考。

1 控制器设计

本文设计的控制器为分层结构。上层为运动跟踪层，采用质心侧偏角和横摆角速度的独立控制，分别计算出实现车辆横摆稳定性控制所需的横摆力矩；并设计对应车辆行驶状态的加权函数；对两控制通道的横摆力矩进行加权求和，作为上层控制器输出即目标横摆力矩。在下层控制器中，分别就轮胎附着裕度优化和电机工作效率区间设计优化算法。结合试验，设计多目标寻优控制器，实现轮胎附着裕度和能耗经济性的综合优化。

1.1 运动跟踪控制器设计

1.1.1参考模型及控制变量理想值

车辆运行在线性区时，忽略轮胎的非线性因素并忽略转向系统、悬架系统的动力学影响，视车辆X轴方向速度分量为常量，只考虑Y轴方向的横向运动和绕Z轴的横摆运动，依据此时车辆状态建立线性二自由度车辆参考模型。此模型对车辆稳定行驶时的行驶状态描述和对驾驶员意图的表述精确度满足车辆行驶控制需求。

(1)

(2)

(3)

式(1)～(3)中：L为等效轴距；K为稳定系数；as为前两桥转角比；Ci(i=1,2,3,4)分别为各桥轮胎的侧偏刚度；δ1为第一桥车轮转向角；Vx为纵向车速。

由微分方程组中质心侧偏角与横摆角速度的关系，同理，易推知质心侧偏角的理想值为：

(4)

1.1.2滑模控制器

以上述参考模型为基础，设计高阶滑模控制器[8]。依据控制结果，计算得到车辆维持稳定性所需的附加横摆力矩。易知考虑附加横摆力矩作用的二自由度微分方程组为：

(5)

首先设计横摆角速度控制，定义滑模面为：

(6)

式(6)中：sγ为横摆角速度控制的滑模变量；c1、c2分别为误差及其变化率的归一化权重，且c1>0,c2>0。

将式(5)代入式(6)得：

(7)

(8)

其中：

(9)

(10)

对式(10)积分得横摆角速度控制下车辆稳定行驶所需的横摆力矩ΔMγ。

(11)

其中：

(12)

1.1.3加权函数及横摆力矩期望值

横摆角速度与质心侧偏角的耦合关系在式(5)有所体现，这说明不可能完全排除某一个变量的影响而单独控制另一个变量。本文通过设置加权函数W，尽量减弱二者之间的互相干扰给控制过程带来的不良影响。依据质心侧偏角与车辆的稳定程度之间的对应关系，建立加权函数。该权值用于规定在联合控制器给出的横摆力矩中2个控制子系统分别给出的力矩之比。根据车辆稳定性与β的关系，设计W的表达式为：

(13)

式(13)中，β0与β1分别为车辆稳定性降低过程中的2个标定状态所对应的质心侧偏角。

最终得到联合滑模控制器的输出控制量ΔMz的大小为：

ΔMz=WΔMγ+(1-W)ΔMβ

(14)

1.2 转矩分配控制器设计

本文设计的转矩分配控制器为多目标优化[9]。首先以提高轮胎附着裕度为目标，对转矩分配进行优化；结合试验，选定阈值；当车辆附着裕度目标函数达到阈值后，即认为车轮附着裕度已满足行驶控制需求，在此基础上开始进行经济性优化，由经济性优化模块给出单轮转矩目标值；若车辆附着裕度目标函数未达到阈值，即认为此时应单纯地提高车辆的稳定程度，即由轮胎力优化模块给出单轮转矩目标值。

考虑到多目标优化存在切换问题，为避免“开关”结构的出现，设计切换函数，使转矩分配控制在车辆行驶过程中始终保持平滑[10]，控制器结构如图1所示。

图1 控制器结构示意图

图1中，Tia为轮胎力优化分配模块输出的各车轮转矩目标值，Tib为轮胎力优化分配模块输出的各车轮转矩目标值，Tic为阈值判定模块输出的各车轮转矩阈值。(此节中若无特殊说明，则Tia、Fib、ηi等中的i=1,2,…,8)。

1.2.1轮胎力优化设计

为提高全车轮胎附着裕度，应通过优化轮胎利用率来实现轮胎力的优化分配[11]。为保证控制的实时性要求，需要适当简化目标函数，主要考虑纵向力与垂向载荷间的关系。综上，设计轮胎力优化目标函数为：

(15)

式中：Fxi为各轮纵向力；Fzi为各轮垂向载荷；μi为各轮路面附着系数。

考虑地面附着及电机限制，得到车轮纵向力约束条件为：

(16)

式(16)中：Tmax为电机最大输出转矩；r为车轮滚动半径。

考虑上述优化问题的优化目标及约束条件，采用加权最小二乘法进行寻优计算。计算得出轮胎力优化后的纵向力Fxia。又因为Tia=Fxia·r，所以该模块输出为Til和Tia。

1.2.2能耗经济性优化设计

首先需要测出驱动电机的工作效率与转矩、转速三者间的对应关系。实验室现有电机工作效率测试台架，包括一台同型号轮毂电机和一台负载电机，如图2所示。

实验时，可以实时测得轮毂电机的输入电压Vi和输入电流Ii及电机输出转矩Ti和输出转速ni[12]。

(17)

(18)

Pinput_i=UiIi

(19)

式(17)～(19)中：ηi为第i车轮电机对应Ti和ni的工作效率；Poutput_i为电机输出的机械功率；Poutput_i为电机输入的电功率。

图2 电机工作效率测试台架

经过一组实验，测得电机的转速、转矩与工作效率的对应关系即MAP图[13]，如图3所示。

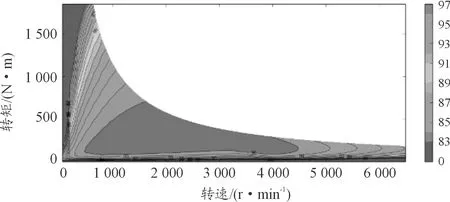
图3 驱动电机转速-转矩-效率MAP图

经济性优化的目的是在保证不影响各个车轮通过协调分配转矩实现上层整车横摆扭矩给定的前提下，调整各车轮之间的扭矩分配；即在各车轮转速一定的情况下，调整分配转矩给定，从而在保证整体扭矩输出的同时，提高整车电机的工作效率，降低能耗。举例而言，某一时刻，当同侧4个电机总共需要输出100 N·m时，而每个车轮实际可输出最大值为50 N·m时，如果没有此控制模块，则将平均分配转矩输出，4个车轮都处于较小扭矩输出状态，效率较低；而施加此模块控制后，采用2个电机各输出50 N·m，另外2个电机随动，则2个耗能的电机都出于大转矩输出状态，效率提高，最终实现能耗经济性优化。综上，设计经济性优化目标函数为：

(20)

式(20)中，ηi=ηi(Ti,ni)通过查MAP图得到。

考虑电机附着、电机功率和稳定性阈值限制，得到约束条件：

Tib≤min{rμiFzi,Tmax,Til}

(21)

1.2.3多目标协调控制

为了研究对象能在充分保证行驶稳定性的基础上，提高能耗经济性，以提高作战半径，发挥更大的武器效能。在设计轮胎力优化模块和经济性优化模块的基础上，设计协调控制模块，其中包含判断模块和切换模块。

车辆行驶过程中，纵向力的约束为：

Fxi≤μimaxFzi

(22)

判断模块中包含一个附着裕度阈值系数σ(0<σ<1)，用来标记轮胎力是否满足动力要求的界限。即当Fxi满足式(23)时，视为充分稳定。

Fxi≤σμimaxFzi

(23)

定义Til作为对应Fxil的转矩稳定阈值：

(24)

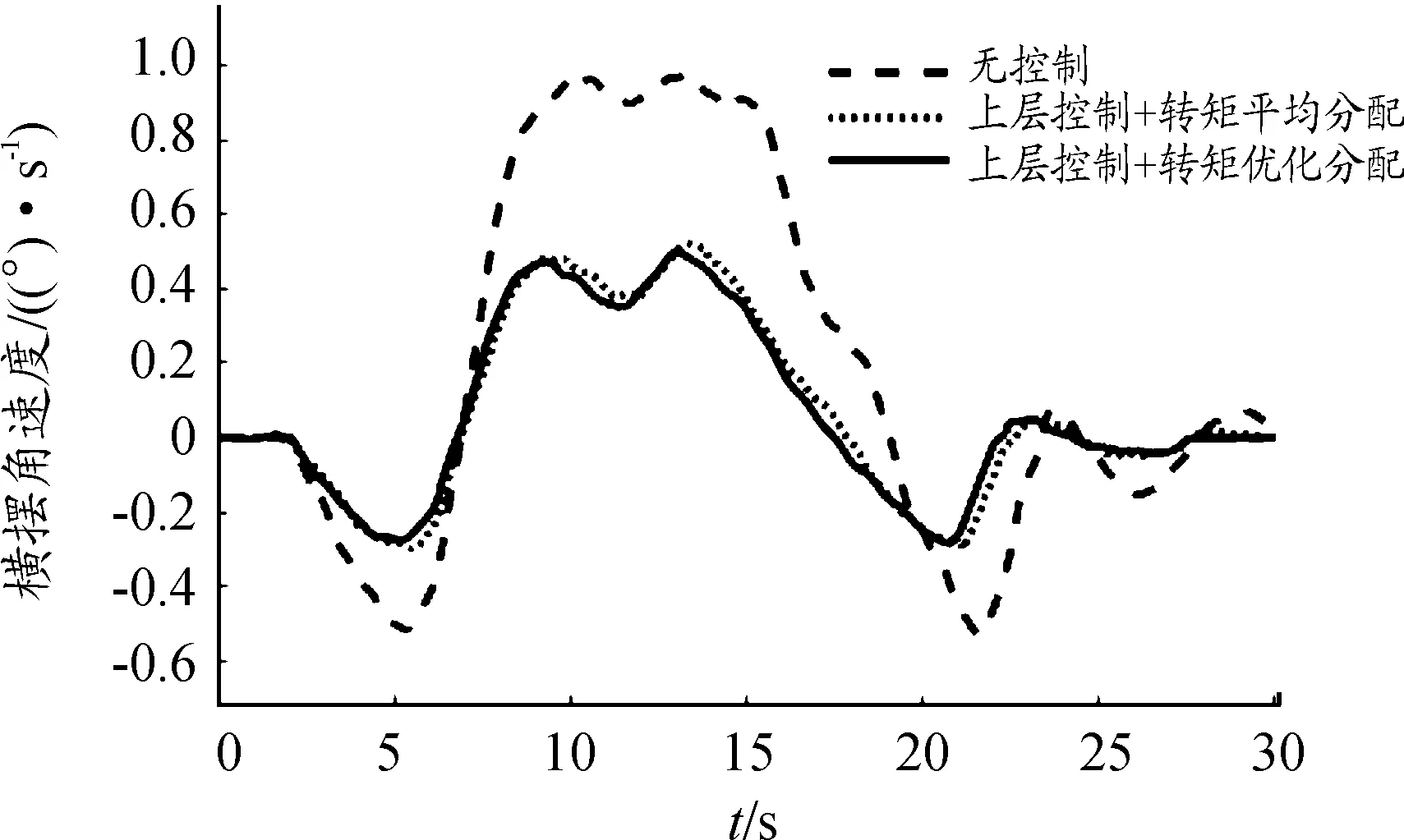
进行稳定性优化计算，得到Tia和Til，若所有Tia≥Til，则认为当前时刻车辆行驶环境足够理想，能完全满足车辆稳定性要求，则在此基础上进行经济性优化。如果存在任意Tia

Tid=Tia(i=1,…,8)

(25)

如果进行经济性优化，则依据前述经济性优化模块可计算出Tib。

但是考虑到多目标切换时，若采用“开关”结构，控制平滑性将变差。所以定义加权函数，以加权求和的形式实现不同目标控制的切换，加权函数为：

Tid=(1-λ)Tia+λTib

(26)

式(26)中：λ为切换参数；Tja={Tia|min[(T1l-T1a),…,(T8l-T8a)]}为一中间变量。λ定义为：

(27)

2 人在环实时仿真验证

2.1 人在环仿真实验平台

人在环实时仿真平台主要包括4部分：用于采集驾驶员加速、制动、转向操纵信号的驾驶员模拟操纵系统；用于车辆行驶控制方法实时仿真的dSPACE系统；用于电机及其驱动控制系统实时仿真的RT-LAB系统；用于车辆动力学实时仿真的Vortex系统。

进行仿真试验时，驾驶员输入通过方向盘、驱动踏板、制动踏板模拟器输入系统，驾驶员信息采集盒实现数模转换，之后信号由dSPACE仿真系统中的控制器接收。控制器同时接收Vortex输入的车辆状态信息，运行控制算法，求解得到转矩控制指令，通过总线发送给RT-LAB仿真系统，RT-LAB将电机实际输出转矩发送给Vortex，驱动车辆实时运行，形成闭环仿真系统[14]。

2.2 试验车辆简介

试验车辆实车原型为“十三五”某型在研多轮独立电驱动车辆，采用八轮轮毂电机独立驱动形式，前两桥具有自然转向结构，整车通过各轮独立转矩控制实现差速转向。

车身尺寸及电机驱动系统部分参数如表1所示。

表1 车辆及电机驱动系统部分参数

2.3 仿真试验及分析

为同时验证车辆上层控制及下层多目标协调转矩分配控制效果，以典型双移线工况为基础，设计了接近研究对象实际行驶特点的试验工况[15-16]。

每组仿真试验连续依次进行A(μ=0.3、目标车速为35 km/h)，B(μ=0.4、目标车速为50 km/h)，C(μ=0.7、目标车速为70 km/h)3种条件下的双移线工况试验，连续完成10组试验。

仿真试验平台可记录各台驱动电机的输入电流、输入电压、转矩和转速,电压与电流相乘即为输入功率,转矩与转速相乘即为输出功率。记录、整理试验数据得到表2。

经过多次试验调整，取定β0=0.03，β1=0.08，σ=0.73。

表2为3次完整试验的能耗统计结果。3次试验均施加相同的上层控制，旨在比较下层转矩分配的控制效果，其中轮胎力优化分配即在设计的转矩分配层中只保留轮胎力优化模块。由表2可以看出，轮胎力优化分配方案单纯考虑了车轮附着裕度问题，行驶能耗高于平均分配方案；而复合目标分配方案在车辆行驶状态较为稳定，轮胎附着裕度较为充分时，能够适时地转换控制目标，合理分配目标转矩，使更多的车轮尽量工作在高效区，从完整行驶过程上看，降低了车辆能耗，提高了能源利用率。

图4至图9为第一组实验中A条件下的仿真结果。

表2 两种分配方式能耗

图4 行驶轨迹

图5 车轮转矩曲线

图6 横摆角速度曲线

图7 质心侧偏角曲线

图8 质心侧偏角相位曲线

图9 轮胎力优化目标函数J曲线

从图4可以看出，未施加控制的车辆在附着率较低的路面进行连续转向行驶时，明显偏离理想轨迹；而加入上层控制后，车辆行驶基本符合驾驶意图，再加上转矩优化分配控制后，车辆循迹能力进一步提升。图5为车辆施加转矩优化分配后的分配结果，以上层控制结果为引导，下层转矩分配模块控制实现了转矩差异分配。图6至图8则具体显示出车辆在连续转向运动中的整车稳定程度，上层控制的施加很好地限制了横摆角速度和质心侧偏角的变化，两变量控制后的最大值分别较控制前降低了42.3%和47.0%；而再加入转矩优化分配后，又分别降低了3.7%和4.5%，同时动态响应的快速性有所提高。

图9为第一组试验中A条件下及A、B两工况间直线行驶过渡阶段的轮胎力优化目标函数J的数据。从图9可以看出，在3～23 s，当车辆处于转向阶段时，绝大多数情况下，判断模块判断Fxi未处于充分稳定状态，转矩优化分配主要以轮胎力优化为主，复合目标优化分配控制的目标函数J与单纯轮胎力优化分配控制相应目标函数取值相同；而在25～40 s，当车辆经过前后两工况过渡路段时，车辆处于直线行驶，行驶环境理想，在一段时间内，判断模块判断Fxi处于充分稳定状态，复合优化目标控制的优化目标从轮胎力优化转为经济性优化，目标函数J的取值稳定在一定范围，而未同单纯轮胎力优化分配控制一样，使目标函数值继续优化下降。

3 结论

本文针对军用多轮电驱动车辆的行驶控制问题，设计了一种分层控制方法，控制器上层通过协调控制质心侧偏角与横摆角速度，给出整车附加横摆力矩目标值；下层转矩分配层，实现了同时考虑轮胎力优化和经济性优化的多目标转矩优化分配。仿真结果表明，上述控制器，能够很好地控制车辆依据驾驶员意图行驶，同时在充分保证轮胎附着裕度的前提下，提高车辆能耗经济性，增加研究对象的作战半径，从多方面促进其更好地发挥武器效能。