基于VI-CarRealTime的FSAE赛车操稳性优化
2020-12-15石晨旭裴晓飞
石晨旭 裴晓飞
摘 要:为提高FSAE(Formula SAE)赛车的圈速,对赛车的操纵稳定性进行仿真优化。首先使用TDFT工具箱中對 Hoosier 43101 R25B轮胎的试验数据进行PAC2002轮胎模型的参数辨识,然后在VI-CarRealTime中建立整车虚拟模型并验证其准确性,最后依据8字绕环和蛇形绕桩工况的仿真结果,优化了侧倾刚度分布、外倾角和前束角等参数。结果表明,优化后的赛车在侧向附着能力和瞬态响应品质方面都有所提升,改善了整车操纵稳定性,同时也为赛车的调教提供了仿真依据。
关键词:FSAE赛车;轮胎模型;整车模型;操纵稳定性
中图分类号:U469.6+96 文献标识码:A 文章编号:1671-7988(2020)22-84-05
Abstract: In order to improve the lap speed of the FSAE (Formula SAE) car, the handling stability of the car is simulated and optimized. First use the test data of Hoosier 43101 R25B tires in the TDFT toolbox to identify the parameters of the PAC2002 tire model, then build a virtual model of the vehicle in VI-CarRealTime and verify its accuracy, and finally based on the 8-word winding ring and snake winding Simulation results of the working conditions optimize the parameters such as roll stiffness distribution, camber angle and toe angle. The results show that the optimized car has improved lateral attachment ability and transient response quality, improved the handling stability of the whole car, and also provided a simulation basis for the tuning of the car.
Keywords: FSAE racing car; Tire model; Vehicle model; Handling stability
CLC NO.: U469.6+96 Document Code: A Article ID: 1671-7988(2020)22-84-05
前言
车辆动力学虚拟仿真技术被广泛应用于车辆的研发与优化中,在减少开发时间、控制成本和提升驾驶性能方面具有巨大的优势。VI-grade为中国大学生方程式赛事(Formula SAE,简称SAE)提供软件赞助支持,在VI-CarRealTime的虚拟环境中,可以快速搭建高精度的动力学模型和虚拟赛道,验证赛车设计,通过优化参数来提升赛车的操纵稳定性。
操纵稳定性仿真分析包括整车建模、赛道建模和评价优化三个部分。轮胎模型参数辨识是整车建模的重要组成部分,对仿真结果有重大影响,使用Matlab和TDFT工具箱可以高效处理轮胎试验数据,得到精准的轮胎模型[1-2];在完成其他子系统的建模和装配后,进行整车模型仿真和试验的关联[3]。由于FSAE赛车的特殊性,传统的国家标准并不适用于评价其操纵稳定性,应基于特定的FSAE赛道,建立虚拟道路模型进行操纵稳定性仿真[4]。由于修改了试验方法,必须重新确定国标评价参数的上下限值,结合FSAE赛车的评分规则确定不同试验项目的评分权重[5],最终依据评分来优化赛车的K&C特性和转向特性等[6-7],提高赛车的操纵稳定性。
本文首先对Hoosier 43101轮胎进行了PAC2002轮胎模型的参数辨识,建立了整车模型并验证了其精度,之后使用8字绕环和蛇形绕桩仿真工况的结果评价操纵稳定性,优化了侧倾刚度分布、外倾角和前束角。最后将两种车型进行圈速仿真,验证优化的有效性。
1 PAC2002轮胎模型
“魔术公式”轮胎模型是一种被广泛应用的计算轮胎稳态工况的力和力矩的半经验轮胎模型,于1987年由荷兰Delft理工大学的H.B.Pacejka教授提出。魔术公式用三角函数的组合公式表达轮胎的纵向力、侧向力、回正力矩[8],其一般表达式如下:
式中:Y可以表示纵向力Fx、侧向力Fy和回正力矩Mz,X为对应的滑移率κ和侧偏角α;B为刚度因子,决定曲线在原点处的斜率;C为形状因子,控制X在变化范围内取极限值时Y的大小,从而决定了曲线的形状;D为峰值因子,决定曲线的峰值;E为曲率因子,控制曲线在峰值处的曲率以及峰值所处的水平位置;SH和Sv分别曲线相对原点的水平和垂向偏移。
PAC2002轮胎模型是以魔术公式为原型,不断完善发展得到的新版本,在原来的基础上增加考虑了瞬态工况的计算,改善了模型的翻转力矩,广泛应用于车辆的操纵稳定性仿真[9]。
2 PAC2002轮胎模型参数辨识
2.1 参数辨识流程
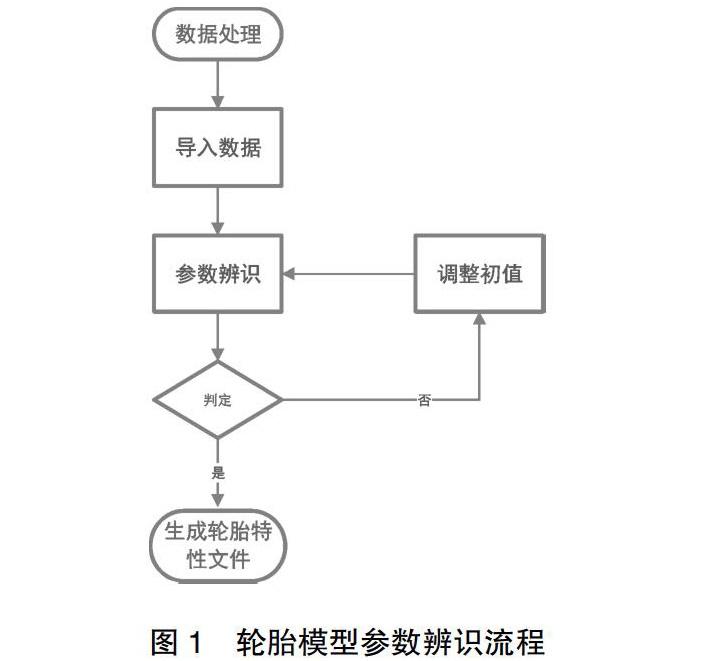
由于PAC2002轮胎模型对胎压变化不具备预测性,故本文只提取常用胎压12 psi下的轮胎六分力试验数据进行轮胎模型的参数辨识。PAC2002轮胎模型参数辨识的基本流程如图1所示。
2.2 试验数据处理
轮胎的试验工况可以分为纯侧倾工况、纯纵向工况和复合工况,提取出相应的数据进行拟合才能完整地表达轮胎力学特性。纯侧向工况下的轮胎试验数据如图2所示,需要删除暖胎阶段下的不稳定数据和每个侧偏角变化周期之间一段侧偏角为0°的无用数据,处理后的数据见图3。在处理纯纵向工况数据时,只需提取侧偏角为0°的试验数据,而复合工况需提取侧偏角为0°、-3°、-6°的试验数据,原始试验数据见图4。
2.3 参数辨识
利用ADAMS的示例文件fm_data_example_tdft和loaded _effective_radius_example_tdft,编辑其中的轮胎测试条件、尺寸信息、计算数据等信息,形成TDFT工具箱可以辨识的tdx格式文件。由于TDFT工具箱采用的坐标系为TYDEX C-Axis和W—Axis轮胎坐标系,而轮胎测试数据遵循SAE坐标系,故需要对垂直载荷FZ数据进行正负变换,侧偏角SA和外倾角IA数据进行单位变化。
将tdx文件导入FDFT工具箱,选择对所有力和力矩进行参数辨识。从结果上看,试验数据与拟合曲线具有较好的一致性,得到的PAC2002轮胎模型精度较高,满足仿真要求。
在实际的赛车跑动中,由于地面的附着条件达不到试验台的高附着要求,胎温也不如轮胎试验时维持在理想温度区间内,所以应对附着系数进行一定的缩放,调整比例因子LMUX、LMUY为0.7[10],使仿真结果更接近实际情况。最后,生成轮胎特性文件并用于后续的操纵稳定性仿真。
3 整车操纵稳定性优化与评价
3.1 整车模型
在VI-CarRealTime中调用整车模型的模板,通过修改尺寸规格、悬架参数和传动方式等来建立动力学仿真模型,赛车基本参数见表1。为验证整车模型的准确性,进行八字绕环工况的仿真,与实车跑动时陀螺仪得到的试验数据相比具有较好的一致性,仿真结果与试验结果如图9所示。
3.2 侧倾刚度分布优化
当赛车处于转向工况时,离心力的作用使得载荷在左、右车轮之间重新分配。由于轮胎的载荷敏感性和侧偏特性,载荷转移将会影响赛车的侧向附着极限与动态平衡。垂直载荷与轮胎侧偏刚度的关系见图10,载荷转移量越大,平均侧偏刚度越小[11]。通过防倾杆控制前、后轴的载荷转移,就可以减少或增加赛车的不足转向趋势。因此,匹配合适的防倾杆刚度,优化前、后轴的侧倾刚度分布改善赛车的动态平衡,从而提高操纵稳定性。
3.2.1 仿真工况
在FSAE赛事的动态测试中,8字绕环和高速避障项目被用来测试赛车的操纵稳定性。8字绕环考察的是赛车的稳态响应,可以用最大侧向加速度或圈时来评估;而高速避障侧重于评价赛车的瞬态响应,包括响应时间和横摆角速度等。高速避障的测试方法和目的类似于蛇形绕桩,因此为了便于仿真,基于高速避障赛道的特点建立蛇形绕桩工况。
MaxPerformance仿真模式通过不断地迭代找到每个点的极限通过速度,从而求出给定轨迹下的最短圈时。导入8字绕环的路径文件和路面文件,设置初速度10 m/s,用该模式来计算赛车的极限状态,8字绕环赛道见图11。
高速避障的平均通过速度在45 km/h左右,其中蛇形绕桩部分桩桶以7.62 m到12.19 m的间隔直线排列。因此,结合国标GB/T 6323-2014[12]的试验方法,仿真工况选择基准车速45 km/h,修改桩桶间距为10 m,在VI-EventBuilder模块中编写驾驶员控制文件,加速和制动模块设置为保持车速,转向模块用如图13所示的路径控制。运用FileDriven仿真模式,导入驾驶员控制文件和路面文件,实现匀速绕桩。
3.2.2 评价指标
8字绕环工况按完成左、右两圈的时间作为评价指标Ns。蛇形绕桩工况参考QC/T480-1999汽车操纵稳定性指标限值与评价方法[13],选择中间四个有效标桩区的平均横摆角速度峰值作為评价指标Nr,计分方法如公式4:
3.2.3 仿真分析
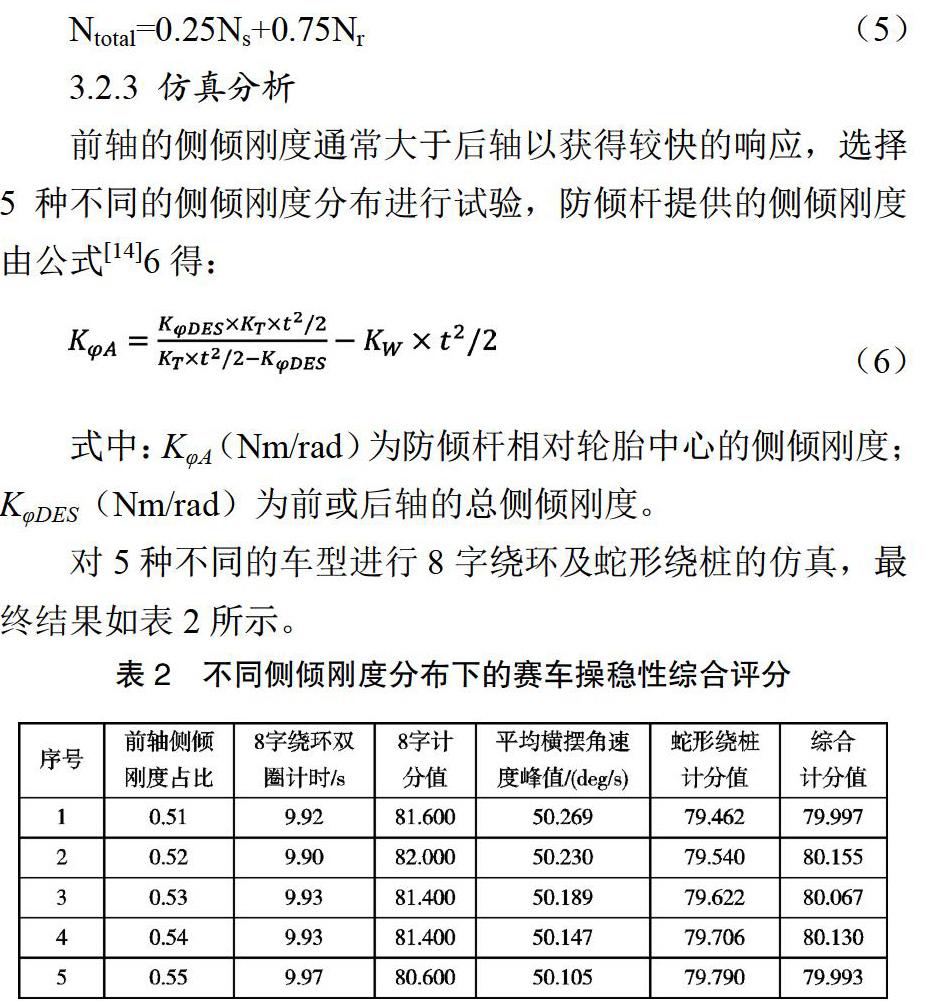
前轴的侧倾刚度通常大于后轴以获得较快的响应,选择5种不同的侧倾刚度分布进行试验,防倾杆提供的侧倾刚度由公式[14]6得:
3.3 外倾角与前束角优化
外倾角会影响轮胎与地面的接触面积,通过设置一个合适的负外倾角,使承受较大载荷的外侧轮与地面保持垂直接触,可以提高侧向附着力。前束角的作用主要是为了减少外倾角带来的行驶阻力,另一个作用是调整赛车对转向初始输入的响应速度。
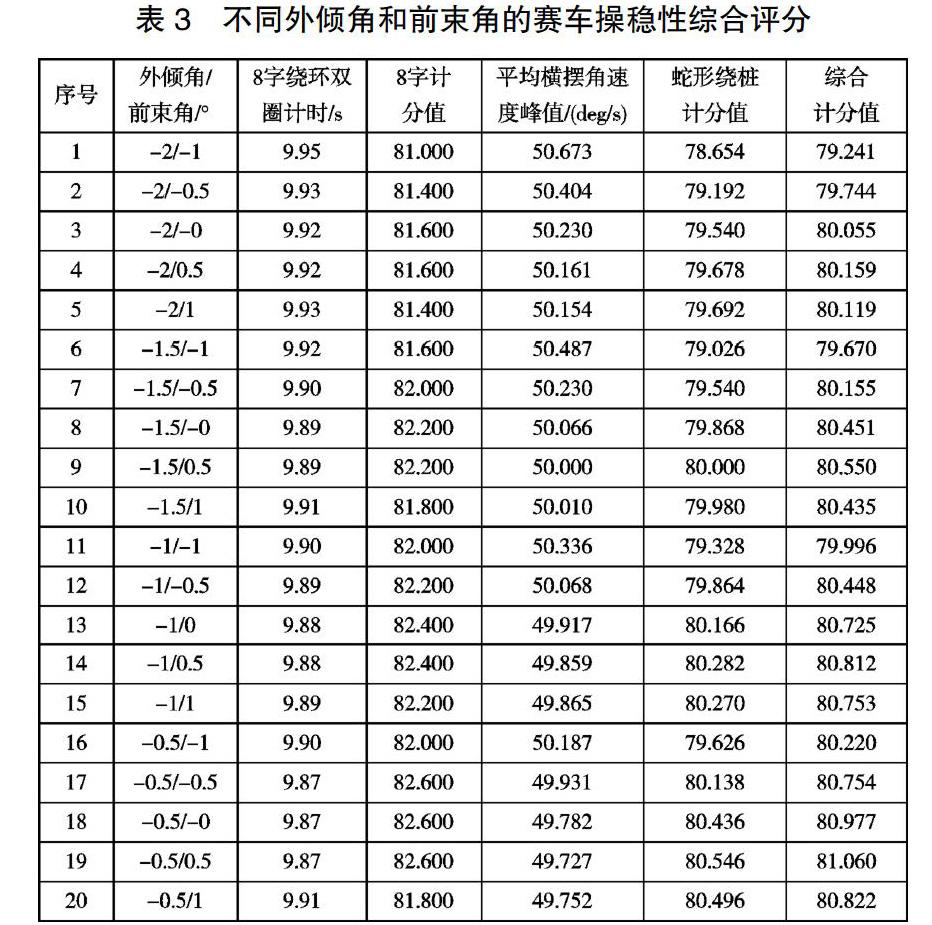
为了便于试验,前、后轴外倾角取相同的值,共4个变量;前轮前束角设置5个变量,后轮前束角取0 °,共形成20组试验对象,仿真工况以及评价指标不变,得到仿真结果如表3所示。
由表3可知,外倾角为-0.5 °,前束角为0.5 °时的赛车操纵稳定性最优。在这种组合下,由于前轮前束角为正,当赛车处于转向工况时,由于提供主要附着力的外侧轮已经指向入弯方向,因此有更快的响应速度和更好的操纵稳定性,但是这种组合没有消除外倾角带来的阻力,会削弱纵向动力性,在实际调教中应该通过数据去评估这些阻力的影响。
4 圈速对比
将原车型与优化后的车型使用MaxPerformance仿真模式分别进行8字绕环与高速避障工况的仿真,求得最快单圈的圈时,高速避障道路模型由VI-CarRealTime提供。原车型的参数为前轴侧倾刚度占比0.51,外倾角-1.5 °和前束角-0.5 °。结果对比见表4,说明优化工作起到了提高操纵稳定性的作用,使赛车能获得更好的成绩。
5 结论
本文建立了Hoosier 43101 R25B轮胎的PAC2002轮胎模型,并搭建了整车虚拟模型。参考国标及结合赛道特点建立评价指标,优化了悬架侧倾刚度分布、外倾角及前束角,将8字绕环的通过时间从9.92s缩短至9.87s,高速避障的圈时从70.42s缩短至69.97s,提升了整车操纵稳定性,为实车调教提供了仿真依据。
参考文献
[1] 刘泽,张新.基于Matlab的FSAE赛车常用轮胎数据处理方法研究[J].轮胎工业,2015,35(5):307-310.
[2] 王海,张宏亮,薛盛兴.基于TDFT的PAC轮胎模型参数辨识[J].汽车实用技术, 2019, (7):62-65.
[3] 刘红领,张德超,孙国良,张林波,徐有忠.悬架侧倾刚度分布对车辆瞬态响应的影响分析[J].机械设计,2015,32(03):12-17.
[4] 邓召文,高伟,臧照阳.基于特定赛道的FSAE赛车操纵稳定性仿真分析[J].拖拉机与农用运输车,2016,43(02):7-11+15.
[5] 洪聪.大学生方程式赛车轮胎模型参数辨识及整车操稳性仿真分析[D].长安大学,2019.
[6] 宋学前,丁华锋,景文倩等.FSAE赛车转向系统优化设计[J].重庆理工大学学报(自然科学), 2019,第33卷(2):38-44.
[7] 张志亮,朱建军.FSAE赛车整车建模及操纵稳定性仿真[J].机械设计与制造,2020, (1):75-79.
[8] Hans B. Pacejka,Tire and Vehicle Dynamics.[M].3.The Netherlands: Delft University of Technology,2012.165-176
[9] 程泽木,姜俊昭,蔡金文等.基于轮胎六分力测试的PAC2002轮胎模型参数辨识方法研究[J].汽车实用技术, 2018, (15):61-64.
[10] Derek Seward.Race Car Design.[M].1.UK:Palgrave,2014.131.
[11] 余志生.汽车理論.[M].6.北京:机械工业出版社,2019.195.
[12] GB/T 6323-2014.汽车操纵稳定性试验方法[S].(GB/T 6323-2014. Controllability and stability test procedure for automo bile[S].)
[13] QC/T480-1999.汽车操纵稳定性指标限值与评价方法[S].(QC/ T480-1999.Criterion thresholds and evaluation of controllability andstability for automobiles[S]).
[14] MILLIKEN W.F., MILLIKEN D. L,Race Car Vehicle Dynamics[M]. Warren dale SAEInternational,1994.
