基于强度折减法的抗滑桩加固边坡可靠度分析
2020-12-15黄俊赵江段祥睿张洁
黄俊 赵江 段祥睿 张洁
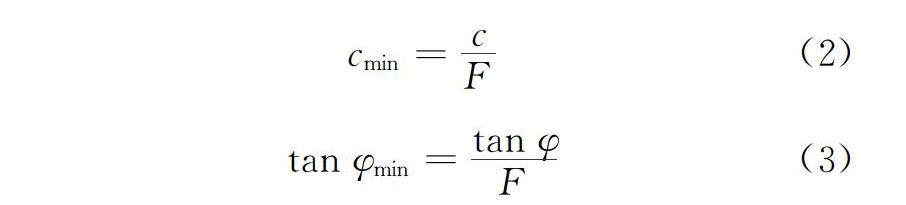
摘 要:抗滑桩是一种常用的边坡加固方法。由于天然土体存在不确定性,导致抗滑桩加固边坡的稳定性也存在不确定性,采用可靠度方法可定量考虑上述不确定性。为更加真实地反映不同抗滑桩加固位置下边坡的滑动面,采用强度折减法来计算边坡的安全系数。基于可靠度理论提出一种抗滑桩加固边坡的稳定性评价方法,采用一阶可靠度与响应面法相结合的方法计算边坡的失效概率。为方便应用,开发了基于FLAC3D的抗滑桩加固边坡可靠度分析程序。采用钢管混凝土桩加固边坡的算例计算结果表明,抗滑桩的加固位置和桩间距对加固边坡的可靠度有重要影响,在相同的桩间距条件下,边坡可能存在一个最优抗滑桩加固位置。
关键词:边坡;抗滑桩;可靠度;强度折减法
中图分类号:TU431 文献标志码:A 文章编号:2096-6717(2020)06-0011-08
Abstract: Piles are widely used to reinforce slopes. Uncertainties exist in stability with anti-slide pile reinforced slope due to the uncertainties of soil. Reliability method can be used to quantify the uncertainties. Shear strength reduction method is employed to obtain the factor of safety and slip surfaces with different pile reinforcement locations. A response surface method-based first order reliability method is used to calculate the failure probability. Based on FLAC3D, an automatic programing procedure is proposed for convenient application.Steel pipe piles are adopted for stabilization in the illustrative example. The results show pile location and spacing have significant effect on the reliability of the illustrative example. An optimal location may exist at a certain spacing for the illustrative example. The suggested method can be helpful for the optimal design of pile reinforcement for soil slopes.
Keywords:soil slopes; piles; system reliability; shear strength reduction method
由于土体是一种复杂的天然材料,性质复杂多变,导致了其力学参数的不确定性,也造成边坡的安全系数难以准确确定。20世纪70年代,Wu等[1]建议采用概率理论考虑边坡稳定性分析中的不确定因素,由此,基于可靠度理论的边坡稳定性分析方法获得广泛的研究[2-3]。多年来,边坡可靠度分析模型多基于工程中常用的极限平衡法[4]。近年来,随着强度折减法的发展,基于强度折减法的边坡可靠度分析日益受到重视[5]。与极限平衡法相比,强度折减法无需对滑动面形状进行假设即可自动搜索最危险滑动面位置,能够更加真实和“自然”地反映边坡的破坏机制[6]。近年来,边坡可靠度分析领域的研究热点逐渐转移到如何考虑土体的空间变异性[7-8]、如何计算边坡的系统失效概率[5,9-11]、如何考慮降雨和地震等荷载的影响[12-13]以及如何使得可靠度方法更为实用化等方面[14-17]。文献[18-19]对边坡可靠度分析方法进行了详细的总结和介绍。
当边坡稳定性不满足要求时,须采用工程措施对其进行加固。由于抗滑桩可在对稳定性扰动较小的情况下对边坡进行加固,该措施在边坡工程中得到广泛应用[20]。已有研究表明,即使在均匀地层中,抗滑桩加固边坡的滑动面也未必为圆弧状,故在抗滑桩加固边坡的稳定性分析中需考虑不规则滑动面的出现[21];此外,随着土体强度参数和抗滑桩位置的改变,滑动面最危险位置也可能发生改变[22]。现有边坡可靠度分析多集中在没有加固体的边坡上[22],仅有少数研究对抗滑桩加固边坡的可靠度进行了分析。其中,文献[23]对给定滑动面采用极限平衡法进行了抗滑桩加固边坡的可靠性分析,没有考虑滑动面位置的不确定性;文献[22]基于圆弧滑动面假设采用极限条分法对抗滑桩加固边坡的可靠性进行了研究,没有考虑滑动面形状的非规则性。如何分析抗滑桩加固边坡的可靠性这一问题尚未得到很好的解决。
强度折减法是边坡稳定性分析中的另外一种常用方法。与极限条分法相比,该方法可自动搜索最危险滑动面形状,既可用于不含加固体的边坡稳定性分析中,也可用于加固后边坡的稳定性分析。文献[24]将强度折减法与传统极限平衡法进行比较,验证了强度折减法在抗滑桩加固边坡分析当中的可行性。文献[24-26]指出,强度折减法除可自动搜寻任意形状最危险滑动面外,还可考虑桩土相互作用,计算获得的安全系数较极限条分法更合理。目前,强度折减法在抗滑桩加固边坡稳定性分析中已获得广泛应用[24-26],在抗滑桩加固边坡的可靠度分析中有很大的应用潜力。笔者提出一种基于强度折减法的抗滑桩加固边坡的高效可靠度分析方法。首先介绍抗滑桩加固边坡的强度折减法模型,再介绍模型的可靠度方法,最后通过算例分析不同因素对抗滑桩加固边坡可靠度的影响,并提出基于可靠度理论的抗滑桩优化设计方法。
1 基于强度折减法的抗滑桩边坡安全系数计算方法
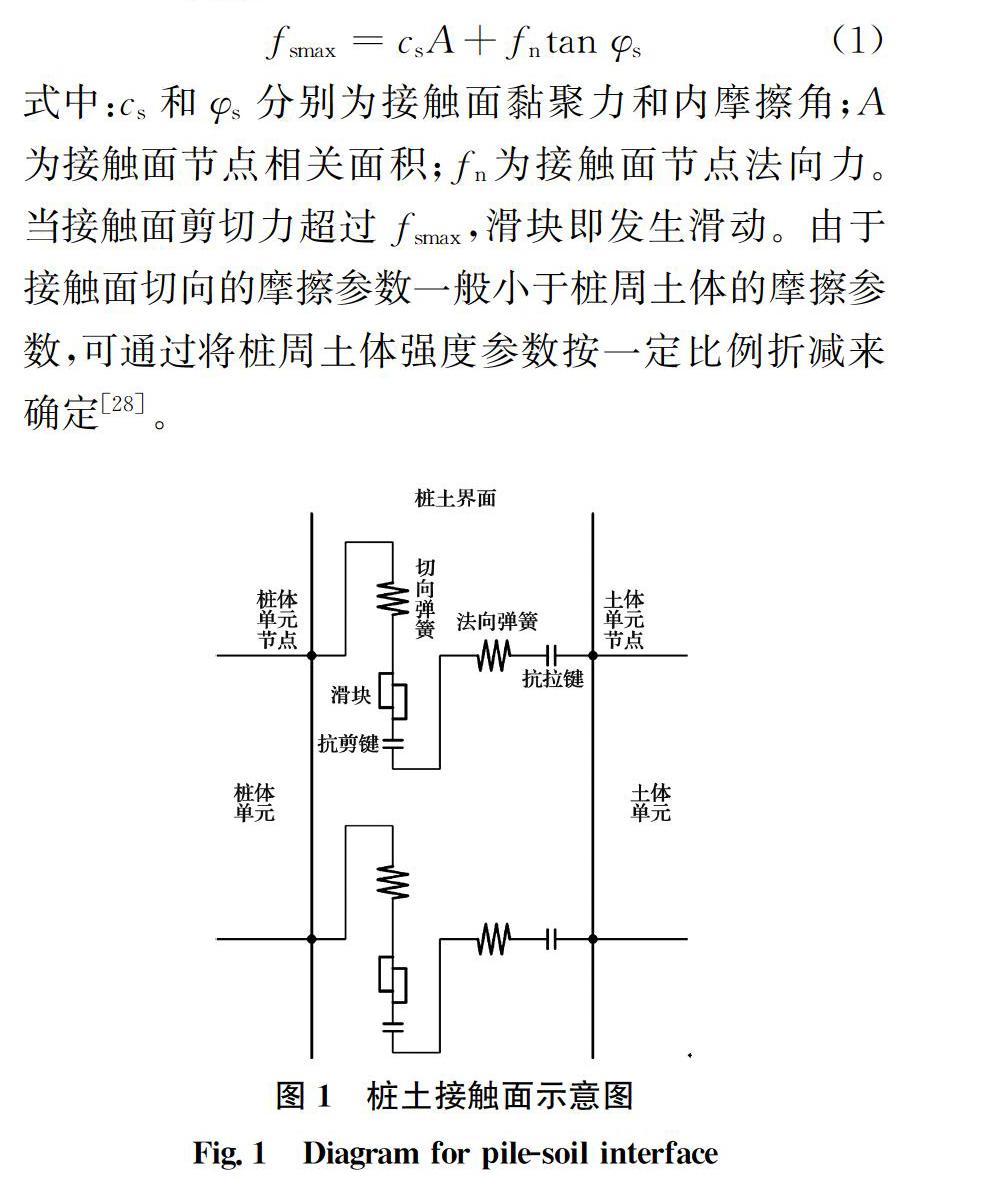
为考虑土拱效应,采用实体单元模拟土体和桩体,其中,土体材料采用摩尔库伦屈服准则、桩体材料采用弹性模型,桩土之间采用可考虑剪切屈服的无厚度接触面进行连接,如图1所示。其中,接触面的法向行为采用法向弹簧和抗拉键来控制;当接触面法向拉力超过最大抗拉强度,接触面即失效。取抗拉键强度为0,即桩土界面不抗拉。接触面的切向行为通过切向弹簧、抗剪键和滑块来表征,抗剪键的强度服从库伦剪切强度屈服准则,其可承受的最大剪切力fsmax按式(1)计算[27]。
式中:cs和φs分别为接触面黏聚力和内摩擦角;A为接触面节点相关面积;fn为接触面节点法向力。当接触面剪切力超过fsmax,滑块即发生滑动。由于接触面切向的摩擦参数一般小于桩周土体的摩擦参数,可通过将桩周土体强度参数按一定比例折减来确定[28]。
式中:cmin和φmin分别为极限平衡状态下的黏聚力和内摩擦角。首先定义一个安全系数的上界和下界,分别用Fu和Fl来表示,使模型对于Fl处于稳定,而对于Fu处于不稳定,即模型的安全系数F介于Fl和Fu之间。然后,检验当安全系数等于(Fl+Fu)/2时,模型是否能够稳定。目前常用的边坡失稳判据主要有3种[29]:1)模型计算不收敛;2)坡体或坡面位移突变;3)潜在滑移面塑性区贯通。如果模型稳定,则采用(Fl+Fu)/2作为新的Fl;否则采用(Fl+Fu)/2作为新的Fu。重复以上步骤,直到Fu和Fl之差小于容许误差,即将(Fl+Fu)/2作为模型的安全系数。
采用FLAC3D实现上述强度折减法,采用最大不平衡力判断模型是否收敛。由于FLAC3D无法对存在弹性单元的模型直接进行强度折减法计算,利用FLAC3D内置的FISH语言编制了基于二分法的抗滑桩安全系数计算程序,仅对土体参数进行折减,对桩土接触面参数不进行折减,再基于最大不平衡力比判断计算是否不收敛。当模型最大不平衡力无法达到某一阈值(如1×10-5)时,认为模型不收敛。为便于判定当前安全系数下模型是否不收敛,首先设置一个足够大的特征步数Nr,并记录连续两个Nr计算步数后的模型最大不平衡力比;如果第2个Nr计算特征步条件下最大不平衡力比超过第1个Nr特征步条件下的最大不平衡力比,则认为模型在当前安全系数下不收敛,否则,模型将进行下一个Nr步数的计算。在任意阶段,如果模型最大不平衡力比小于设定的阈值,则认为模型在当前安全系数下收敛。取Nr=20 000,不平衡应力比阈值设为1×10-5。上述方法可用于计算抗滑桩加固边坡的安全系数,也可用于计算未加固边坡的安全系数。
钢筋混凝土桩由于造价低廉、抗滑效果好,在中国获得了广泛应用。其他国家除采用钢筋混凝土抗滑桩以外,还常采用钢管混凝土桩作为抗滑桩[30-31]。由于施工速度快,近年来,钢管混凝土桩在中国滑坡应急抢险等项目中也开始获得应用[32]。在本文模型中,桩体采用弹性材料进行模拟,通过采用等效参数,既可模拟钢筋混凝土抗滑桩,也可模拟钢管混凝土桩。
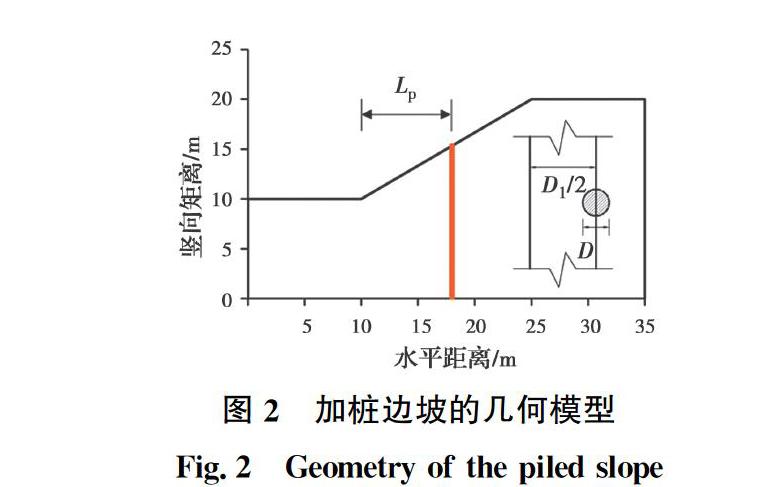
为验证上述方法的可靠性,采用该方法对文献[21]中某钢管混凝土抗滑桩加固边坡的安全系数进行分析。图2为该边坡的剖面图。该边坡高10 m、坡度为2∶3。土体黏聚力c为10 kPa、内摩擦角φ为20°。土体的弹性模量、泊松比和重度分别是200 MPa、0.25和20 kN/m3。边坡采用直径为0.8 m的钢管混凝土桩进行加固,其弹性模量、泊松比和重度分别是60 GPa、0.2和78.5 kN/m3。图2中Lp为抗滑桩中心距离坡脚的水平距离,D为桩的直径,D1为桩间距(桩心距)。
图3为Lp=7.5 m、D1=2D条件下边坡的有限差分模型。为考虑土体从桩间的滑动失稳,采用三维模型对抗滑桩加固边坡进行分析。为减少计算量,模型采用半对称形式。模型边界条件与文献[21]相同:竖直边界施加水平位移约束,底部边界施加水平和竖直方向的位移约束,抗滑桩桩底也施加水平和竖直方向位移约束。基于提出的强度折减法,表1给出了两种工况条件下不同方法获得的安全系数。由表1可知,由该方法获得的安全系数与文献[21]中强度折减法获得的安全系数也很接近;两者之间的微小差别可能是由模型网格的差别造成的。
2 基于响应面法的抗滑桩加固边坡可靠度分析模型
对于一个边坡,通常将土体强度参数作为随机变量,用x表示。根据强度折减法计算得到安全系数以后,可建立抗滑桩加固边坡的功能函数g(x)。
式中:y为随机变量x转换到标准正态空间中的变量;R为随机变量的相关矩阵。由式(5)可以看出,可靠度的求解是一个有约束优化问题。式(5)使得表达式最小化对应的点yd常被称为设计点。
當采用强度折减法计算抗滑桩加固边坡的安全系数时,功能函数为隐式。此时,采用式(5)进行可靠度分析时涉及可靠度分析与强度折减法的耦合,极难进行求解。利用响应面法,采用一个具有显示表达式的函数对原功能函数进行近似,再通过该显示表达式进行可靠度分析,从而实现隐式表达式与可靠度分析的解耦。令G(y)代表标准空间中的功能函数。对于大多数岩土工程问题,其功能函数可采用式(6)所示方程进行局部拟合。
3 抗滑桩加固边坡可靠度分析程序
为方便工程应用,基于MATLAB和FLAC3D开发了抗滑桩加固边坡可靠度分析程序,其中MATLAB作为可靠度分析的工具,FLAC3D用来计算各取样点功能函数的响应值。在MATLAB中,可利用命令!flac3d700_gui.exe实现对FLAC3D的调用。再通过生成text文本的方法,实现MATLAB和FLAC3D的数据交换。
首先,MATLAB生成取样点数据并将其保存在text文本中。FLAC3D读取文本中取样点并计算各取样点的功能函数响应值。FLAC3D的计算结果也将保存于text文本中,然后MATLAB读取取样点响应值并建立响应面函数,并利用MATLAB中的fmincon.m解决的式(5)优化问题并获取可靠度指标。通过式(7),可以更新取样中心点并建立更新响应面逼近真实的设计点。一般,当前后两次可靠度计算误差在容许误差范围内,则认为计算收敛。具体的可靠度迭代流程可参考图4所示流程图。
4 算例分析
作为算例,假设图2中边坡土体黏聚力服从均值为10 kPa、变异系数为0.3的对数正态分布,内摩擦角服从均值为20°、变异系数为0.2的对数正态分布。首先,设置响应面拟合步长m=1,根据流程图4对未加固的边坡进行可靠度分析。其迭代过程如表2所示,对应的可靠度指标和失效概率分别为0.800和21.19%,表明边坡在未加固条件下失效概率较大。表2表明,迭代经过2次收敛,说明提出的方法具有很高的计算效率。采用应变增量云图[34],图5给出了设计点对应的滑动面位置。图5表明,不加固条件下边坡可能发生整体滑动。
采用相同的方法对Lp=8 m、D1=2D条件下抗滑桩加固边坡进行可靠度分析,其迭代过程如表3所示。加固后边坡对应的失效概率0.34%。为了验证方法的准确性,采用蒙特卡罗法基于对上述加固后边坡的可靠度进行分析。当样本数为100 000时,基于一台搭载CPU为一颗Intel Core i9 9900ks 5.0 GHz的计算机,计算耗时约970 h,获得的失效概率为0.29%,失效概率变异系数为5.71%,结果与该方法计算结果接近。采用相同的计算机,采用该方法计算时间为2.2 h。
由此可以看出,抗滑桩可显著降低边坡的失效概率。图6给出了此时设计点对应的滑动面。可以看到,在抗滑桩的作用下,边坡的滑动面位于抗滑桩下侧,滑坡可能性和规模都有所降低。提出的方法可以量化抗滑桩对滑坡可靠性的影响。
4.1 抗滑桩位置的影响
为研究抗滑桩位置对边坡可靠度的影响,图7给出了桩间距为D1=2D、Lp分别为2、6、10、14 m时边坡设计点处滑动面位置及其可靠度指标。由图6和图7可知,抗滑桩的位置对滑动面位置和边坡的可靠度指标有重要的影响。当Lp≤6 m时,滑动面位于抗滑桩上方,可靠度指标随着抗滑桩向滑坡中部移动而增加;当Lp≥8 m时,边坡滑动面位于抗滑桩下方,可靠度指标随着抗滑桩向滑坡顶部移动而减小。
4.2 抗滑桩桩间距的影响
为了研究抗滑桩桩间距对边坡稳定性的影响,图8(a)~(c)给出了Lp=8 m,D1=3D、D1=4D、D1=5D条件下设计点处的滑动面位置和可靠度指标。由图8可知,随着桩间距增大,可靠度指标逐渐减小,边坡的失效概率也随之增大。此外,可以看到,随着桩间距增大,滑动面逐渐趋近于未加固时的圆弧状,说明加固效果逐渐下降。此外,桩间不同位置处的滑动面也有差异,图8 (d)为Lp=8 m、D1=5D时,桩间土中心处的滑动面,与图8(c)桩心处相比,桩间土更接近未加固时的圆弧状,表明在抗滑桩加固条件下滑动面具有的空间特性,说明强度折减法能够更加真实地反映边坡破坏机制。
4.3 抗滑桩最优位置
图9给出了不同桩间距条件下边坡可靠度指标随抗滑桩加固位置的变化情况。由图9可以看到,对于所研究的案例,在给定桩间距条件下,边坡的可靠度指标均随抗滑桩位置变化呈现先增大后减小趋势,即可能存在一个最佳的加固位置;在给定加固位置条件下,可靠度指标随桩间距的增加而减小。这些结论与文献[21,25-26]采用确定性分析方法所得出的结论一致。文献[35]建议路基边坡的目标可靠度为βt=2.3。从图9中可知,按D1=3D、Lp=7~ 9 m可达到上述可靠度指标。
5 结论
可靠度方法可以定量考虑岩土参数不确定性对边坡稳定性的影响。现有研究多集中于未加固边坡的可靠度分析。针对该问题,提出一种基于可靠度理论的抗滑桩加固边坡稳定性评价方法。该方法采用强度折减法来计算边坡的安全系数,采用响应面法计算边坡的失效概率。为方便应用,开发了基于FLAC3D的抗滑桩加固边坡可靠度分析程序。算例分析表明,提出的方法具有很高的计算效率。算例采用的抗滑桩为钢管混凝土桩,结果表明,抗滑桩的加固位置和桩间距对该边坡的可靠度有着重要的影响。在相同的桩间距条件下,该边坡可能存在一个最优抗滑桩加固位置。提出的方法可用于基于可靠度理论的抗滑桩加固边坡优化设计。参考文献:
[1] WU T H, KRAFT L M. Safety analysis of slopes [J]. Journal of the Soil Mechanics and Foundations Division, 1970, 96: 609-630.
[2] 祝玉学, 戚国庆. 边坡可靠性分析的蒙特卡洛-有限元法[J]. 水文地质工程地质, 1992, 19(3): 17-20.
ZHU Y X, QI G Q. Monte Carlo-finite element method for slope reliability analysis [J]. Hydrogeology and Engineering Geology, 1992, 19(3): 17-20. (in Chinese)
[3] 陳祖煜, 徐佳成, 孙平, 等. 重力坝抗滑稳定可靠度分析: (一)相对安全率方法[J]. 水力发电学报, 2012, 31(3): 148-159.
CHEN Z Y, XU J C, SUN P, et al. Reliability analysis on sliding stability of gravity dams: Part Ⅰ,An approach using criterion of safety margin ratio [J]. Journal of Hydroelectric Engineering, 2012, 31(3): 148-159. (in Chinese)
[4] 彭振斌, 李俊, 彭文祥. 基于Bishop条分法的边坡可靠度应用研究[J]. 中南大学学报(自然科学版), 2010, 41(2): 668-672.
PENG Z B, LI J, PENG W X. Application analysis of slope reliability based on Bishop analytical method [J]. Journal of Central South University(Science and Technology), 2010, 41(2): 668-672. (in Chinese)
[5] MA J Z, ZHANG J, HUANG H W, et al. Identification of representative slip surfaces for reliability analysis of soil slopes based on shear strength reduction [J]. Computers and Geotechnics, 2017, 85: 199-206.
[6] GRIFFITHS D V, LANE P A. Slope stability analysis by finite elements [J]. Géotechnique, 1999, 49(3): 387-403.
[7] 李典庆, 祁小辉, 周创兵, 等. 考虑参数空间变异性的无限长边坡可靠度分析[J]. 岩土工程学报, 2013, 35(10): 1799-1806.
LI D Q, QI X H, ZHOU C B, et al. Reliability analysis of infinite soil slopes considering spatial variability of soil parameters [J]. Chinese Journal of Geotechnical Engineering, 2013, 35(10): 1799-1806. (in Chinese)
[8] 陈朝晖, 雷坚, 黄景华, 等. 考虑参数空间变异性的边坡稳定可靠性有限元极限分析[J]. 岩土工程学报, 2018, 40(6): 985-993.
CHEN Z H, LEI J, HUANG J H, et al. Finite element limit analysis of slope stability considering spatial variability of soil strengths [J]. Chinese Journal of Geotechnical Engineering, 2018, 40(6): 985-993. (in Chinese)
[9] 褚雪松, 王旭春, 張勇强, 等. 基于代表性滑动面的边坡系统可靠度分析[J]. 煤炭学报, 2014, 39(6): 1077-1083.
CHU X S, WANG X C, ZHANG Y Q, et al. Slope system reliability analysis based on representative slip surfaces [J]. Journal of China Coal Society, 2014, 39(6): 1077-1083. (in Chinese)
[10] 蒋水华, 祁小辉, 曹子君, 等. 基于随机响应面法的边坡系统可靠度分析[J]. 岩土力学, 2015, 36(3): 809-818.
JIANG S H, QI X H, CAO Z J, et al. System reliability analysis of slope with stochastic response surface method [J]. Rock and Soil Mechanics, 2015, 36(3): 809-818. (in Chinese)
[11] 曾鹏, 陈语, 李天斌. 基于拟牛顿近似二阶法的岩土工程系统可靠性分析[J]. 岩石力学与工程学报, 2018, 37(3): 726-733.
ZENG P, CHEN Y, LI T B. System reliability of geotechnical problems using quasi-Newton approximation-based sorm [J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(3): 726-733. (in Chinese)
[12] HUANG H W, WEN S C, ZHANG J, et al. Reliability analysis of slope stability under seismic condition during a given exposure time [J]. Landslides, 2018, 15(11): 2303-2313.
[13] ZHANG L L, LI J H, LI X, et al. Rainfall-induced soil slope failure: Stability analysis and probabilistic assessment [M]. CRC Press, 2018.
[14] 李亮, 褚雪松, 郑榕明. Rosenblueth法在边坡可靠度分析中的应用[J]. 水利水电科技进展, 2012, 32(3): 53-55, 66.
LI L, CHU X S, CHENG Y M. Application of Rosenblueth method in reliability analysis of soil slopes [J]. Advances in Science and Technology of Water Resources, 2012, 32(3): 53-55, 66. (in Chinese)
[15] 苏永华, 罗正东, 张盼凤, 等. 基于Kriging的边坡稳定可靠度主动搜索法[J]. 岩土工程学报, 2013, 35(10): 1863-1869.
SU Y H, LUO Z D, ZHANG P F, et al. Active searching algorithm for slope stability reliability based on Kriging model [J]. Chinese Journal of Geotechnical Engineering, 2013, 35(10): 1863-1869. (in Chinese)
[16] TAN X H, WANG X E, HU X J, et al. Two methods for predicting reliability index and critical probabilistic slip surface of soil slopes [J]. Geotechnical and Geological Engineering, 2016, 34(5): 1283-1292.
[17] 任斌斌, 苏立君, 张崇磊, 等. 基于Python语言和Abaqus平台的边坡可靠度计算自动化算法开发[J]. 土木与环境工程学报(中英文), 2019, 41(5): 67-72.
REN B B, SU L J, ZHANG C L,et al. A slope reliability automated algorithm based on python language and abaqus platform [J]. Journal of Civil and Environmental Engineering, 2019, 41(5): 67-72. (in Chinese)
[18] 刘晓, 唐辉明, 熊承仁. 边坡动力可靠性分析方法的模式、问题与发展趋势[J]. 岩土力学, 2013, 34(5): 1217-1234.
LIU X, TANG H M, XIONG C R. Patterns, problems, and development trends of analysis methods for slope dynamic reliability [J]. Rock and Soil Mechanics, 2013, 34(5): 1217-1234. (in Chinese)
[19] 王德洋, 朱鴻鹄, 张洁, 等. 基于可靠度理论的边坡稳定性研究进展[J]. 工程地质学报, 2016, 24(Sup): 1010-1018.
WANG D Y, ZHU H H, ZHANG J,et al. Status and prospects of research on slope stability based on reliability theory [J]. Journal of Engineering Geology, 2016, 24(Sup): 1010-1018. (in Chinese)
[20] 李荣建, 于玉贞, 李广信. 土质边坡中部与顶部抗滑桩动力响应和边坡变形比较[J]. 山地学报, 2010, 28(2): 135-140.
LI R J, YU Y Z, LI G X. Analyses of deformation of slopeand dynamic response of stabilizing piles reinforced in the middle and near crest of slope in earthquake [J]. Journal of Mountain Science, 2010, 28(2): 135-140. (in Chinese)
[21] WEI W B, CHENG Y M. Strength reduction analysis for slope reinforced with one row of piles [J]. Computers and Geotechnics, 2009, 36(7): 1176-1185.
[22] ZHANG J, WANG H, HUANG H W, et al. System reliability analysis of soil slopes stabilized with piles [J]. Engineering Geology, 2017, 229: 45-52.
[23] LI L, LIANG R Y. Reliability-based design for slopes reinforced with a row of drilled shafts [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2014, 38(2): 202-220.
[24] 郑颖人, 赵尚毅. 用有限元强度折减法求边(滑)坡支挡结构的内力[J]. 岩石力学与工程学报, 2004, 23(20): 3552-3558.
ZHENG Y R, ZHAO S Y. Calculation of inner force of support structure for landslide/slope by using strength reduction FEM [J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(20): 3552-3558. (in Chinese)
[25] CAI F, UGAI K. Numerical analysis of the stability of a slope reinforced with piles [J]. Soils and Foundations, 2000, 40(1): 73-84.
[26] WON J, YOU K, JEONG S, et al. Coupled effects in stability analysis of pile-slope systems [J]. Computers and Geotechnics, 2005, 32(4): 304-315.
[27] Itasca Consulting Group. FLAC3D: Fast Lagrangian Analysis of Continua in Three-Dimensions [M]. Ver. 7.0. Minneapolis: Itasca, 2019.
[28] 張建勋, 陈福全, 简洪钰. 被动桩中土拱效应问题的数值分析[J]. 岩土力学, 2004, 25(2): 174-178, 184.
ZHANG J X, CHEN F Q, JIAN H Y. Numerical analysis of soil arching effects in passive piles [J]. Rock and Soil Mechanics, 2004, 25(2): 174-178, 184. (in Chinese)
[29] 吕庆, 孙红月, 尚岳全. 强度折减有限元法中边坡失稳判据的研究[J]. 浙江大学学报(工学版), 2008, 42(1): 83-87.
LV Q, SUN H Y, SHANG Y Q. Slope failure criteria of shear strength reduction finite element method [J]. Journal of Zhejiang University(Engineering Science), 2008, 42(1): 83-87. (in Chinese)
[30] FRANK R, POUGET P. Experimental pile subjected to long duration thrusts owing to a moving slope [J]. Géotechnique, 2008, 58: 645-658.
[31] SONG Y S, HONG W P, WOO K S. Behavior and analysis of stabilizing piles installed in a cut slope during heavy rainfall [J]. Engineering Geology, 2012, 129/130: 56-67.
[32] 杨雪莲, 邬凯, 何思明, 等. 大直径旋挖钢管混凝土桩滑坡应急抢险与工后变形监测[J]. 路基工程, 2019(1): 184-190.
YANG X L, WU K, HE S M, et al. Large-diameter rotary-drilled concrete-filled steel pipe piles for landslide emergency rescue and the deformation monitoring after construction [J]. Subgrade Engineering, 2019(1): 184-190. (in Chinese)
[33] ANG A H, TANG W H. Probability concepts in engineering planning and design, Vol. II: Decision, risk, and reliability [M]. New York, John Wiley & Sons, 1984.
[34] CHENG Y M, LANSIVAARA T, WEI W B. Two-dimensional slope stability analysis by limit equilibrium and strength reduction methods [J]. Computers and Geotechnics, 2007, 34(3): 137-150.
[35] 王仲锦, 吴敏敏, 程爱君, 等. 铁路路堤边坡的可靠度设计方法研究[J]. 铁道工程学报, 2013, 30(3): 24-27, 49.
WANG Z, WU M M, CHENG A J, et al. Study on design method for slope reliability of railway embankment [J]. Journal of Railway Engineering Society, 2013, 30(3): 24-27, 49. (in Chinese)
(编辑 王秀玲)
