Seismic data denoising based on data-driven tight framedictionary learning method

Abstract: Because of various complicated factors in seismic data collection, the random noise of seismic data is too difficult to avoid. This random noise reduces the quality of seismic data and increases the difficulty of seismic data processing and interpretation. Improving the denoising technology is significant. In order to improve seismic data denoising result, a novel method named data-driven tight frame (DDTF) is introduced in this paper. First, we get the sparse coefficients of seismic data with noise by DDTF. Then we remove the smaller sparse coefficient by using the hard threshold function. Finally, we get the denoised seismic data by inverse transform. Furthermore, the DDTF is compared with curvelet transform in the stimulation and practical seismic data experiments to validate its performance. DDTF can raise the signal-to-noise ratio of seismic data denoising and protect the effective signal well.

Keywords: DDTF dictionary; hard threshold; curvelet transform; random noise

0 Introduction

In the process of seismic exploration, the random noise caused by the environmental impact is always accompanied, which serious interferes the effective signal and greatly increases the difficulty of data processing. In order to avoid the influence of random noise brought by the environment, many algorithms have been studied so as to raise the signal-to-noise ratio of seismic data. At present, the proposed methods include F-X deconvolution, polynomial fitting, F-K filtering and so on. But when F-X deconvolution suppresses random noise, it also strengthens all coherent information in seismic data, which causes new interference in effective signals (Chengetal., 2018).

In recent years, in order to remove the random noise effectively and get higher SNR, many geophysicists use the sparsity and separability of seismic data in a basic function transform domain to achieve the effect of denoising. In the processing, different transformation methods are selected to adapt to the sparsity of seismic data. But once the basis function of the transformation method is fixed, it can not be adjusted according to the local characteristics of seismic data. Although wavelet transform can recognize seismic data in multi-scale, its direction recognition is poor. As for Curvelet transform, it inherits the multi-scale recognition ability from wavelet transform and also has directionality (Yuetal., 2019). However, the basis function of curvelet transform is still very difficult to adapt to the seismic data. Therefore, Eladetal. (2006) proposed a super complete dictionary which can sparse decompose seismic data flexibly (Elad & Aharon, 2006). But due to limitations of the dictionary learning algorithm, the dictionary training is not ideal, and its denoising effect is not satisfactory.

One of the decisive factors for the effective representation of seismic signals is to train an accurate super complete dictionary. In this paper, DDTF based on hard threshold is proposed, which can adapt to all kinds of seismic data, so that the trained dictionary can make good use of distinguish the sparse difference between effective signal and noise. In this paper, the layered synthetic seismic record with random noise is tested to compare the denoising ability of DDTF with curvelet transform and verify that the denoising effect of DDTF is better than that of curvelet transform.

1 Method and principle

Dictionary learning is a kind of method that it can sparse represents the signal texture features adaptively. The typical representative is K-SVD (k-singular value decomposition, K-SVD) dictionary learning, which is an improvement of MOD(Method of optimal directions, MOD). It can sparse represent complex seismic data adaptively. But it takes a long time to calculate and is very difficult to process large amount of data. In order to improve the calculation efficiency, many kinds of dictionary learning methods are proposed, such as ADMM dictionary learning, SGK dictionary learning, on-line dictionary learning and DDTF dictionary learning(Zhang, 2018). Among them, DDTF (data-driven tight frame) can not only ensure the accuracy, but also effectively improve the calculation speed, which is the research focus of seismic denoising at present.

DDTF adds tight frame constraints to KSVD:DTD=I.

The optimization can be expressed as follows(Yuetal., 2015):

(1)

Among them,Xrepresents the training sample selected from the seismic data with interference term,Drepresents the dictionary,Arepresents the dictionary sparse coefficient,Irepresents the unit matrix,T0represents the sparse constraint parameter, and the superscriptTrepresents the transposition of the matrix. ║·║Fand ║·║0represent Frobenius norm andl0norm respectively.

There are two steps in DDTF: sparse coding and dictionary updating. First, we should fix the initial dictionary, and then solve the sparse coefficient. Then we update the dictionary by singular value decomposition. And the result of Eq. (1) is obtained by hard threshold function (Schönemann, 1966; Zouetal., 2006).

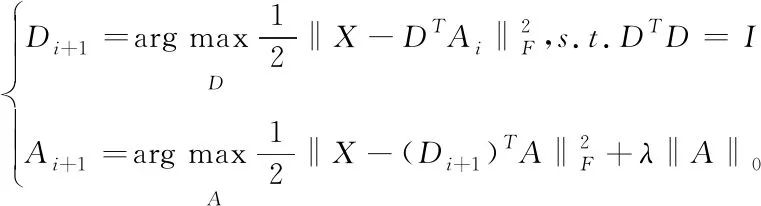
(2)

λis the regularization parameter

(3)

Fig.1 Hard threshold function

(4)

2 Experimental data

In order to verify the superiority of DDTF in removing random noise of seismic signal, we compared it with curvelet transform. What is more, DDTF and curvelet algorithm are used to denoise the simulation data. Therefore, we add random noise to the seismic record and compare the denoising effect of two methods by calculating the signal-to-noise ratio before and after processing. In this paper, the signal-to-noise ratio is defined as:

(5)

Among them,xis the denoised data,x0is the original data, which is the seismic data without random noise.

The following figures is a 90 channel seismic record with 900 sampling points and a sampling rate of 0.001 s (Fig.2a), the seismic record with random noise (Fig.2b), the denoising results of the two algorithms (Fig.3) and the DDTF dictionary (Fig.4).

Compared with Fig.3, it can be seen that both the DDTF and the curvelet transform have significant denoising effects. But compared with the latter, the DDTF remains more effective waves, while the curvelet algorithm loses part of the reflected signals. Moreover, DDTF can remove random noise better than curvelet transform. Table 1 shows that the signal-to-noise ratio of DDTF after denoising is about 1 dB higher than that of curvelet transform. It can also be seen from Fig.5 that the effect of DDTF denoising is significantly better than curvelet transform denoising.

Fig.2 Layered model synthetic seismogram (a) and seismic records with added noise (b)

Fig.3 Layered model synthetic seismogram DDTF effect (a) and curvelet transform effect (b)

Fig.4 DDTF

Table 1 Layered model synthetic seismogram curvelet transform and DDTF SNR before and after denoising

Fig.5 SNR of layered model synthetic seismogram with noise and SNR after reducing random noise by two methods

When the added noise increases gradually, the signal-to-noise ratio of DDTF decreases more slowly than that of the curvelet algorithm. So we can see that the curvelet algorithm losses a part of the effective signal, and the effect of removing random noise is unsa-tisfactory. DDTF can not only eliminate noise, but also protect reflected signal.

3 Detection and analysis of actual seismic records

In order to test the denoising ability of DDTF and curvelet transform in actual data, we use the two methods to deal with actual seismic data. The actual seismic data record is shown in Fig.7. There are 120 traces of the data, sampling time of 256 ns and a sampling rate of 0.001s.

Comparing the results of the two denoising algorithms (Fig.8), we can see that the effect of DDTF denoising is significantly different from that of curvelet transform. First of all, for the noise signal, the effect of DDTF denoising is better than the curvelet. It can be seen from the comparison between Fig.8a and Fig.8b. Although the curvelet transform has removed the noise, some of the events are obviously missing. It shows that DDTF has protected the effective seismic signal well while removing the noise effectively.

Fig.6 Actual seismogram DDTF

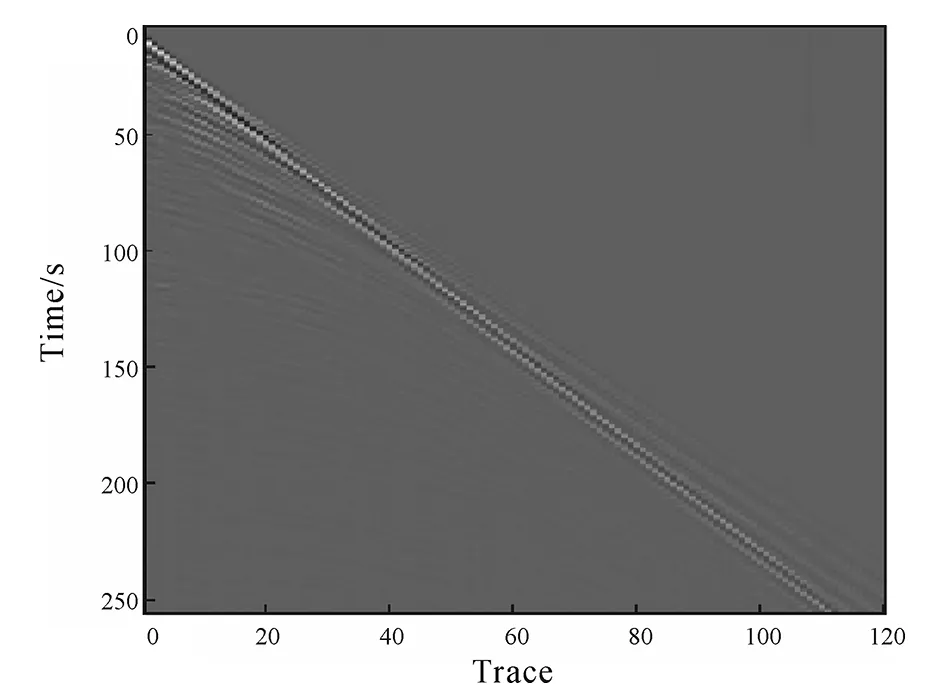
Fig.7 Actual seismogram

Fig.8 DDTF denoising effect (a) and Curvelet transform effect (b)

4 Conclusions

In this paper, we add tight frame constraints based on KSVD dictionary learning and higher calculation accuracy is obtained. Through the comparison of theoretical model test and actual data, the following conclusions are drawn:

(1) DDTF can effectively remove the noise in the seismic record and significantly improve the signal-to-noise ratio of seismic data. It can protect the seismic signal well and avoid the loss of effective reflection signal, which provides strong support for the subsequent interpretation of seismic data.

(2) In the experiment of this paper, compared with the curvelet transform, the denoising effect of DDTF is greatly improved. When the accuracy is higher, DDTF has better performance. With the gradually strengthen of random noise in the seismic record, the denoising effect of DDTF is better than that of curvelet transform and the signal-to-noise ratio of data after denoising decreases more slowly.

(3) DDTF method also has the disadvantage, such as slow operation speed. So the method in this paper is suitable for the small scale seismic data with high precision requirement.