鱼类目标的密度估计模型

2020-12-15汪梦婷袁飞程恩

哈尔滨工程大学学报 2020年10期

汪梦婷，袁飞，程恩

(1.水声通信与海洋信息技术教育部重点实验室(厦门大学)，福建厦门 361005;2.山东省计算机网络重点实验室，山东济南 250014)

鱼类水产养殖业中，从最初的引入苗种、计算养殖密度评估养殖生物量到最后的出售环节，都涉及到鱼类的计数需要。人工作业在耗费巨大人力物力的同时是接触型作业，会对鱼体造成不同程度的损伤，不利于鱼类的生长和出售。为了取代人工作业，有学者结合数字图像处理技术实现鱼的计数这一任务[1-3]。这些方法都是基于目标检测的方法，即将目标在图像中检测出来后以目标检测结果作为计数结果。此外一些学者采用的是基于回归分析的方法，即对目标检测区域提取区域特征，根据区域内的目标数量拟合区域特征和目标数量之间的关系。如拟合目标区域的面积与目标数量之间的线性关系[4-8]，拟合目标区域细化后骨架的端点数[9-10]，或结合目标区域的多种特征预测目标数量[11]。同时一些学者尝试通过设计鱼道完成目标计数[12-14]。随着神经网络的发展，在20世纪90年代就有学者利用人工神经网络达到计数的目的[15]。深度学习网络在不同计算机视觉任务中取得斐然的成绩后，研究人员利用深度学习对鱼类进行了分类[16]、识别[17-19]、定位[20]、摄食欲望判断和测长测重[21-22]等研究。但是利用深度学习对目标识别进行计数仍然是基于目标检测和回归分析的方法。这些方法应用条件比较严格，实际应用会受到以下几种挑战：首先目标计数结果受限于检测结果，而检测方法对环境噪声较敏感；其次目标遮挡重叠时计数精度会大大降低；最后检测区域的特征如像素面积等与鱼类数量的关系在不同鱼类或同一鱼类的不同生长阶段都不相同，不具有普适性。

近年来深度学习在人群密度估计方面取得了优越的发展并应用于公共安全事业中。人群密度估计事先获得人群图像的密度图，密度图表示了场景中人群分布情况，对密度图积分或求和就能获得场景中的人群总数。目前人群密度估计在ShanghaiTech[23]、UCSD[24]、UCF_CC_50[25]等开源数据集上都获得了较高的估计精度。

虽然人群密度估计取得了较大成功，但是基于深度学习的密度图估计方法目前并没有在水产养殖业中尝试过。基于此，本文提出一个用于鱼类目标密度估计的网络结构。鉴于目前并没有适用鱼群密度估计的数据集，本文创建了一个包含近2 000张样本的鱼群图像数据集并对鱼体进行标注获得了密度图，以实践鱼群密度估计，同时在鱼类数据集和人群数据集上验证了本文方法的有效性。

1 鱼类密度估计网络

Loy等[26]提出，对密集群体的分析可分为3类方法：基于检测的方法、基于回归的方法和基于密度估计的方法。而基于深度学习的方法在计数性能上往往优于传统方法[27]。基于深度学习的密度图估计是指通过训练神经网络得到输入图像相应的密度分布图，对密度图积分得到输入图像中目标数目。

深度神经网络得到迅速发展后，很多学者对利用深度学习分析人流密度进行了尝试。本文中鱼类密度估计网络是一个端到端的神经网络，由前端和后端两个部分组成。前端网络由于提取图像特征，生成特征图。后端网络的输入是前端网络提取的一系列特征图，根据特征图估计输入图像的密度图。鱼类密度估计网络结构如图1所示。

1.1 混合空洞卷积

1.1.1 卷积层

卷积层是卷积神经网络中最重要的组成部分也是卷积神经网络名字的由来。神经网络中，卷积是2个矩阵的点积运算。如图2所示，卷积层的输入是5×5大小的二维矩阵，卷积核大小是3×3，卷积核从上到下、从左到右以步长s扫描输入矩阵与相应区域的点积和是输出矩阵中对应位置的元素值：

(1)

式中：N是卷积核大小；Hi是卷积核H的第i个元素值；Ii是输入图像中Hi对应位置的像素值；y是卷积的输出结果。

图1 鱼类密度估计网络结构Fig.1 The architechture of fish density estimation network

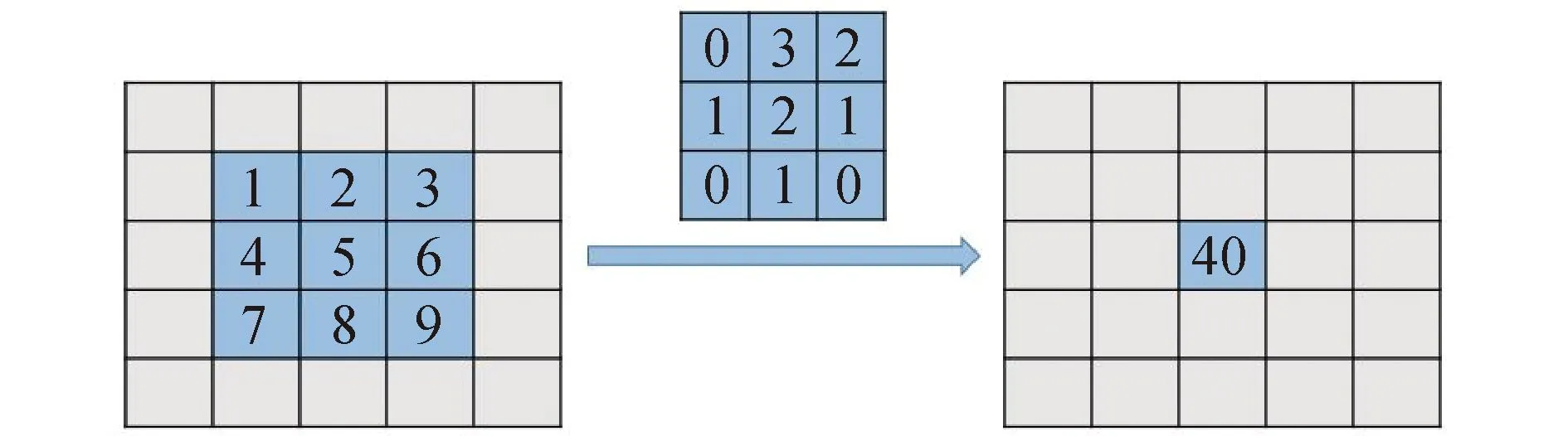
图2 卷积运算示意Fig.2 Illustration of convolution operation

一般的，输入图像边长为w时，输出特征图边长o的计算方法为：

(2)

式中：s是卷积核每次移动的步长；k是卷积核大小；p是卷积操作前对输入图像的补零填充值，目的是使卷积核移动时可以刚好把所有像素遍历完；⎣·」是向下取整运算。

1.1.2 空洞卷积

空洞卷积是Yu等[28]提出的一种卷积结构，最初应用在图像分割领域，目的是为了在不减小图像尺寸的同时增大图像感受野。空洞卷积定义为：

(3)

式中：x(m,n)是长宽分别为M、N的输入图像信息，经过卷积核w(i,j)得到空洞卷积的输出y(m,n)。其中r是空洞率，当r=1时空洞卷积就是普通卷积。边长为K的卷积核经过空洞率为r的空洞卷积操作后边长会变为K+(K-1)(r-1)。

感受野rf(reception field)是指卷积神经网络每一层输出的特征图上的像素点在原始图像上映射区域的大小。例如图2中输出结果40是由输入图像中一个3×3的区域映射得到的，因此卷积核的RF是3×3，即输出结果的每个像素与原始图像的3×3大小的区域有关。大小为3×3的卷积核经过空洞率为1、2的空洞卷积操作后分别得到5×5、7×7大小的卷积核，在不增加网络参数的前提下扩大了卷积层的感受野，如图3(a)所示。普通卷积增大感受野必须将图像下采样，即减小图像大小，而减小图像大小必然丢失部分信息。空洞卷积在保持图像大小的同时能够增大感受野。如图3(b)，设置步长s=1，填充p=0，5×5大小的输入图像经过2次3×3大小的卷积核操作后输出结果大小为1×1，即2次3×3卷积操作的感受野是5，即输出结果是由原始图像中5×5大小的区域映射得到的。图3(b)中，通过增大空洞卷积的空洞率就能改变卷积核的感受野，空洞率越大，感受野越大，即不改变输入图像大小也不增加网络参数。

图3 3×3卷积核感受野示例Fig.3 Example of receptive field with kernel size 3×3

1.1.3 混合空洞卷积

空洞卷积虽然在改变图像大小、不增加网络参数的同时能增大卷积核的感受野，但也存在缺点：“网格效应”。空洞卷积运算时空洞率越大，像素的利用率越小。例如图3(b)中，r=2时卷积核感受野为5×5，但是对卷积运算结果有贡献的只有其中9个像素，像素利用率为36%，r=3时卷积核感受野为7×7，对卷积运算结果有贡献的仍然只有9个像素，像素利用率约为18%。同时，这9个像素来自原图像中不同的块，即空间上的连续性较差，导致输出特征图中相邻像素间的相关性很差，出现明显的分区现象形成“网格效应”。

Wang等[29]发现，卷积层连续采用相同的空洞率时原始图像中部分像素将始终不能参与运算，即部分信息完全丢失。图4(a)是连续采用3×3、r=2时每层卷积的感受野，中心浅色网格是每次卷积的运算结果，深色网格是每次卷积的感受野。从图中看出，连续采用相同空洞率的卷积时原始图像中部分像素始终没有参与运算，造成部分信息丢失。

混合空洞卷积HDC(hybrid dilation convolution)是Wang等[29]提出用于解决空洞卷积“网格效应”的方法。不同于采用不变的空洞率，混合空洞卷积将连续几个卷积层设为一组，组内采用不同空洞率的卷积。例如图4(b)，卷积核大小为3×3，空洞率分别为1、2、3时顶层特征图即最终输出结果的是由原始图像中完整连续的区域得到的。这样的设计使图像感受野没有空洞或缺失，所有的像素都参与了卷积的运算。例如图4(b)中组内空洞率为1、2、3时，最后一层卷积结果的感受野覆盖的是原始图像中一片连续区域，避免了部分像素信息的丢失，卷积结果在空间上具有连续性，解决了空洞卷积的“网格效应”。

图4 “网格效应”和混合空洞卷积示例Fig.4 Illustration of “gridding artifact” and HDC

将连续的几个卷积层作为一组，为了使组内最后一层卷积的感受野对应原始输入图像中一块完整连续没有缺失的区域，组内卷积层的空洞率选择需要满足一定条件：定义组内第2层空洞卷积核非零元素间的距离为M2，则M2不大于原始卷积核大小K：

M2=max[M3-2r2,M3-2(M3-r2),r2]

(4)

式中M3=r3，r2是组内第2层空洞卷积的空洞率。当K=3时，[1,2,5]是有效的空洞率组合，因为M2=2，而[1,2,9]不是有效的空洞率组合，此时M2=5。

1.1.4 网络结构

鱼类密度估计网络由前端网络和后端网络组成。前端网络采用VGG-16[30]的前10层，用于提取输入图像的特征图，输出特征图大小是输入图像的1/8。VGG网络具有很强的特征提取能力，在密度估计中常常被用于构成前端网络提取图像特征[31-32]。后端网络由4个级联的混合空洞卷积组构成，每组由3个连续的空洞卷积组成，基于空洞率的组合原则，组内空洞率为[1,2,3]。表1是本文鱼类密度估计网络的配置。

表1 鱼类密度估计网络参数配置Table 1 Configuration of fish density estimation network

基于深度学习的密度估计方法本质上是特征提取器和密度函数的组合。不同于传统密度函数估计方法，基于深度学习的密度估计不需要人为选择图像特征和构造密度函数模型，相比人为构造的密度估计函数，神经网络对非线性有更强的表达能力。这种将每个像素映射为密度值的方法一定程度上降低了目标遮挡重叠对计数结果的影响。本文将鱼的头部作为检测区域标记整个鱼体。网络训练时，前端网络学习到的是鱼头部的特征，虽然鱼群存在一定程度上的重叠，但是没有被完全遮挡的部分还是能够被前端网络提取到特征，并经后端网络映射为像素点对应的密度值，这部分像素对鱼类计数是有贡献的。

2 实验与结果

2.1 创建鱼类密度估计数据集

目前并没有一个公开的鱼群数据集能用以密度估计。为了训练鱼群密度估计网络，本文首先创建了鱼群密度估计数据集。首先本文在YouTube视频网站上选择下载了20个鱼群视频并截取视频帧获得了大量的鱼群图像。视频分辨率为1 280×720，帧率为30 f/s。为了减少图像的重复率提高数据集的多样性，本文在每个视频的图像帧中抽样选取了适合用于网络训练的图像组成鱼群密度估计数据集。最后本文的数据集共包含1 961张图像，其中1 382张为训练集，579张为测试集，鱼个体总数达到17 442个。

和人群密度估计数据集标注一样，本文对鱼的头部进行标注。同时采用几何自适应高斯核函数生成密度真值图。假设一条的头部标注点位置为xn，则含有N个标注点的信息表示为：

(5)

基于几何自适应的高斯核密度图表示为：

(6)

(7)

对包含一个目标标注点的图像进行高斯滤波并归一化后，滤波结果就是该标注点对应的密度图，所有标注信息滤波结果的加和就是原始图像的密度图。以标注点为中心的(6σ+1)×(6σ+1)区域内的像素都被赋予了相应密度值，越靠近中心点密度值越大，σ近似表示了目标区域大小。根据几何距离确定高斯函数的方差是因为几何距离反映了鱼类头部区域的大小：当鱼群较密集时，鱼类之间的遮挡重叠导致图像中显示的鱼的头部区域变小，此时几何距离相应的也较小；当鱼群分布较稀疏时，鱼群之间的遮挡重叠较少，图像中鱼的头部区域较大，此时几何距离也较大。因此文中采用基于几何自适应的高斯核滤波生成密度真值图。实验中本文采用的β值为0.3。鱼类数据集样本如图5所示。

图5 鱼类数据集样本Fig.5 Samples of fish dataset

2.2 模型训练

本文在实验中将每个样本均等裁剪成4等分，并随机上下或左右旋转图像以此扩充训练数据集。采用L2范数作为网络训练的损失函数：

(8)

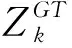
2.3 鱼类数据集密度估计结果

为对比本文所提方法的有效性，实验选取了MCNN[23]、CSRNet[27]、CANNet[33]、DSNet[34]作为对比模型并采用相同的参数设置进行训练。在鱼类数据集上各模型密度估计结果在图6中展示。从图中看出本文提出的密度估计网络结果更接近输入图像的真实值，预测结果更可靠。同时，鱼类密度估计网络对不同种类、不同大小的鱼类图像能保持较好的估计结果。在鱼类数据集样本充足的情况下，密度估计网络能学习到具有很强表达性的特征，对不同种类、不同大小的鱼类估计具有更强的鲁棒性。

图6 鱼类数据集密度估计结果Fig.6 Density estimation results of fish dataset

为了定量的分析网络预测结果，本文采用平均绝对误差MAE(mean absolute error)、均方误差MSE(mean square error)、峰值信噪比PSNR(peak signal to noise ratio)和结构相似性SSIM(structural sIMilarity)来评价网络密度估计的结果：

(9)

(10)

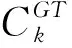
各模型指标对比结果如表2所示，表中深色字体表示最优结果。由表中数据可得，本文提出的鱼类密度估计网络在各项指标上均取得最优结果。在图像结果和指标量化2方面，本文的密度估计网络网络计数结果更准确，估计的密度图更接近真实的密度图。

表2 鱼类数据集网络预测结果对比Table 2 Comparison of networks on fish dataset

2.4 ShanghaiTech密度估计结果

人群密度估计数据集ShanghaiTech是由上海科技大学搜集创建的开源数据集，也是人群密度估计中使用最频繁、最经典的数据集，共包含1 198张图像，330 165个注释头。该数据集分为A和B 2个部分。

2.4.1 ShanghaiTech Part_A密度估计结果

ShanghaiTech Part_A部分图像随机选自Internet，共482张图像，其中训练集300张，测试集182张，图像分辨率不定，人群分布较密集，平均每张图像人群数量达到501个。为对比本文提出的密度估计网络在其他数据集上的预测结果，实验室选择了CSRNet[27]、MCNN[23]、CMTL[35]3个密度估计网络作对比试验，密度估计结果在图7中展示。实验中同样对各模型预测结果进行了定量评价，各指标评价结果如表3所示。表中深色字体表示最优结果，斜体表示次优结果。本文密度估计网络ShanghaiTech Part_A上预测时在各项指标上都获得了最优或次优的结果。

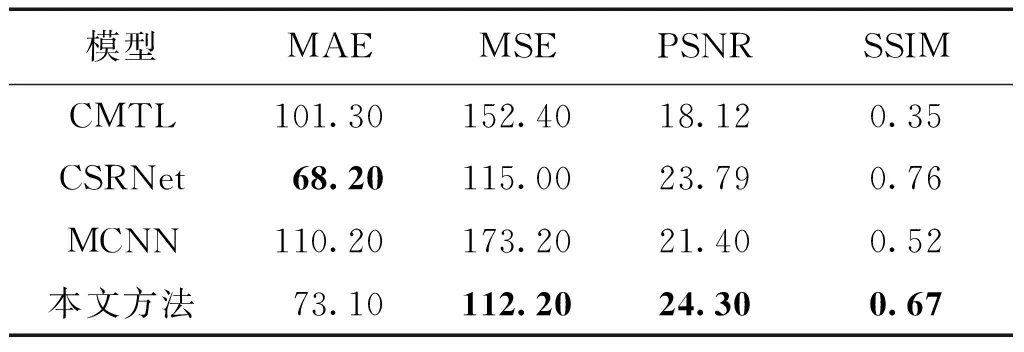
表3 ShanghaiTech Part_A网络预测结果对比Table 3 Comparison of networks on ShanghaiTech Part_A

2.4.2 ShanghaiTech Part_B密度估计结果

ShanghaiTech Part_B部分图像来自上海街道的一些场景，共716张图像，其中训练集400张，测试集316张，该部分图像分辨率固定为768×1 024，人群密度分布相比Part_A较稀疏，平均每张图像人群数量为123。对比试验设置和Part_A部分相同，密度估计结果如图8所示，定量分析结果在表4中展示。表中深色字体表示最优结果。本文密度估计网络ShanghaiTech Part_B上预测时在各项指标上都获得了最优结果。