基于K-means图像深度聚类的自适应Retinex算法

吴明祥 于瓅

摘要：传统的Retinex算法均是采用固定尺度对雾天图像整体进行去雾增强，但是对局部雾霾浓度分布不均的图像，自适应性较弱，图像细节增强也有所欠佳。基于此提出一种基于K-means图像深度聚类的自适应Retinex算法。该算法通过暗通道原理获取雾天图像的景深，用K-means聚类算法对图像深度进行聚类，以深度所属不同类别来估计局部雾天浓度，将相似深度的图像划分成不同子图，并自适应的获取尺度进行增强，最后对子图进行融合，完成对图像整体的增强。结果表明，相对于传统的多尺度Retinex算法和其他去雾算法，文中算法对于图像局部具有较好的自适应成像增强效果，在图像细节增强、颜色重建恢复等方面均表现良好。

关键词：图像增强;自适应成像;图像重建恢复;Retinex;K-means

中图分类号：TP391        文献标识码：A

文章编号：1009-3044（2020）28-0028-05

Abstract： The traditional Retinex algorithm uses a fixed scale to enhance the fog image as a whole， but for the image with uneven local haze concentration distribution， the adaptability is weak， and the image detail enhancement is also poor. Based on this， an adaptive Retinex algorithm based on K-means image depth clustering is proposed. In this algorithm， the depth of field of fog image is obtained by the principle of dark channel， and the depth of image is clustered by K-means clustering algorithm. The local fog concentration is estimated by the difference of depth. The image of similar depth is divided into different subgraphs， and the adaptive acquisition scale is enhanced. Finally， the subgraphs are fused to complete the overall the image  enhancement. The results show that， compared with the traditional multi-scale Retinex algorithm and other defogging algorithms， the algorithm in this paper has a better adaptive imaging and enhancement effect for the local image， and performs well in image detail enhancement， color reconstruction-restoration and other aspect.

Key words： Image enhancement; Adaptive imaging; Image reconstruction-restoration; Retinex; k-means

近年來，雾天图像增强[1～3]作为计算机图像处理领域的研究重点之一，出现了很多的经典算法。LAND等人[4]基于色彩恒常性理论提出了Reinex算法，为图像增强提供了新思路，并在图像去雾上得到越来越多的应用。G.A.WOODELL等人[5，6]提出了单尺度Retinex算法（Single-Scale Retinex，SSR）和多尺度Retinex算法（Multi-Scales Retinex，MSR），将其应用到雾天图像增强上;D.J.JOSHON等人[6]提出了带色彩恢复的MSR算法（Multi-Scales Retinex with Color Restoration， MSRCR），提升了图像色彩恢复效果;汪贵荣等人[7]提出了基于照度分割的多尺度Retinex算法，加强了图像的亮度细节。

研究成果表明，MSRCR对于雾天图像有较好的增强效果。然而该算法通过多个尺度增强后进行加权平均，虽取得一个较为折中的增强效果，却也导致结果在细节处理上欠佳，并对于局部雾霾浓度分布不均的图像，算法也不能实现局部动态的增强。

何凯明等人[8，9]提出的基于暗通道先验的图像去雾算法（简称HE算法），利用暗原色和雾天退化模型估计出大气散射模型参数，具有良好的去雾效果。HE算法指出图像中局部雾霾浓度大小与图像景深（深度）成正相关性，雾霾浓度越大，景深越大，反之越小。

本文提出了一种基于K-means图像深度聚类的自适应Retinex算法。该算法以雾霾浓度和图像景深的正相关性为依据，通过K-means算法[10]将原始图像分割成深度相似的子图，将各子图的Retinex尺度依照图像深度进行线性映射求解，再对子图进行自适应的单尺度Reinex算法增强，依照子图在原始图像中的位置融合子图，实现对图像的增强。

1 Retinex算法理论

1.1 单尺度Retinex和多尺度Retinex算法介绍

Retinex算法基于色彩恒常性理论[11]，认为图像中物体表面信息由自身特性决定，与周围环境无关。由此原始图像[sx，y]分解为入射分量[lx，y]和反射分量[rx，y]：

2 K-means的图像深度聚类算法

传统的Retinex算法都只是图像全局性增强，即使MSR考虑到不同尺度对增强的影响，但本质上只是利用多个尺度加权平均获得折中效果，未考虑局部性差异。为了更好地对雾天图像局部区域进行增强，由暗通道原理图像深度不仅与图像中物体与拍摄者的远近有关，与图像中雾的浓度也成正比，雾的浓度越大，图像深度越深，反之越浅。因此利用图像深度来获知图像中雾的分布和浓度，对图像进行分割，再使用不同尺度对子图进行增强，增强后的图片提升了图像细节，除雾效果更好。

K-means算法以距离作为数据对象间相似性度的标准，数据间距离越小，相似性越高，越有可能同属一类簇。由于图像局部深度变化平缓，确定不同深度的阈值变得困难，且随着不同场景雾天图像的加入，图像深度聚类的复杂度也增加。由此文中运用MinBatchKMeans算法[12]，该算法基于K-means，对数据进行抽样生成数据子集，再进行聚类。自适应的分类不同景深，在應对不同场景的有雾图像也具有自适应性。MinBatchKMeans算法相对原有算法降低了计算时间，利用随机采样降低样本中噪音点的影响，避免出现不同类别中样本数过多或过少的情况。具体流程和示例如图2、3所示。

从图3（b）看出，雾霾浓度加大导致图像局部信息有所丢失，景深随之变大。完成图像深度聚类后，可以得到一个明显带有色彩边界的图像（c），由（c）图对原始图像进行分割，进行自适应尺度的增强。

3 基于K-means图像深度聚类的自适应Retinex算法

3.1一种可变滤波器

上文分析可知，图像局部景深[d]与雾的浓度成正相关。根据Retinex增强理论，当尺度[σ]较大时，图像颜色保真性较好，但增强效果较差，适用于雾霾浓度低的场景;当[σ]较小时，图像增强细节较好，但全局性较差，适用于雾浓度较高的场景。基于此，图像深度[d]与尺度[σ]也具有正相关性。文中定义了一种可变滤波器，根据各图像中不同景深[d]计算自适应的[σ]值。

将图像深度在聚类后分为n块（n为聚类的个数）不同深度去区间的子图，遍历子图中的景深值，得到子图的平均深度，公式如下：

3.2基于K-means图像深度聚类的自适应Retinex算法

综上所述，本文提出一种基于K-means图像深度聚类的自适应Retinex算法。该算法首先基于暗通道原理获取原始图像的深度图像，其次用K-means对深度图像进行聚类处理，再依据可变滤波器求解不同深度区域的尺度，之后根据不同尺度多次对图像使用带有颜色增益加权的单尺度Retinex算法，依据各深度图在原始图像上的对应关系，将不同子图进行融合，完成图像的自适应去雾增强，算法流程如图4所示：

基于此流程，得出[n]个去雾子像（[n]由聚类个数决定），每张子像都完成了自适应增强。再依据子图对应原图的位置，对每张子图进行融合，得到最终结果，公式如下：

4 实验与分析

文中实验的图像均取自不同场景下的雾天图像，考虑到计算时间成本，图像聚类的K值选择5，子图的数目[n]=5。实验主要分为两个部分：第一步设置不同大小的尺度阈值[σ_max]和[σ_min]，用文中算法对多个图像进行增强，通过数据对比，评价不同尺度阈值的增强效果;第二步将文中算法与He算法、MSRCR和自动色彩均衡快速算法（ACE）[13]算法的增强效果进行比较。

4 .1选取[σ]阈值范围

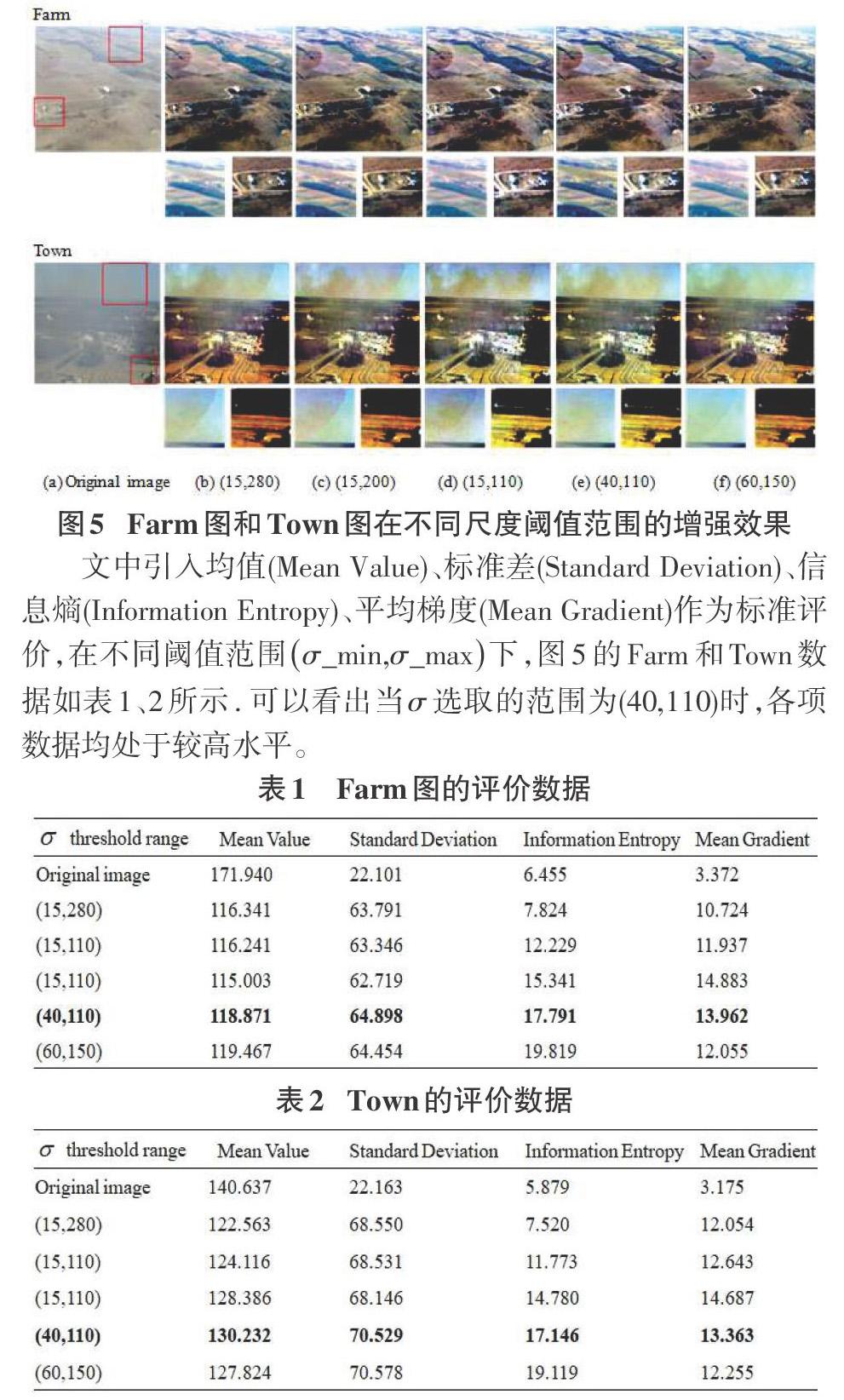
图5是不同尺度阈值下对图像增强后的结果，[σ_min]和[σ_max]分别选取了（15，280）、（15，200）、（15，110）、（40，110）、（60，150）五组数据进行对比。从图5的（b）（c）（f）看出，阈值[σ]选取的范围越大，图像的亮度越暗、颜色越深，局部颜色失真产生边缘现象;如（d）（e）所示，当阈值范围较小时，增强的细节较好、颜色较为自然。

文中引入均值（Mean Value）、标准差（Standard Deviation）、信息熵（Information Entropy）、平均梯度（Mean Gradient）作为标准评价，在不同阈值范围[σ_min，σ_max]下，图5的Farm和Town数据如表1、2所示. 可以看出当[σ]选取的范围为（40，110）时，各项数据均处于较高水平。

文中引入折线图来显示阈值范围与增强效果之间的关系，如图6所示，当[σ]的范围从（15，280）到（60，150），图像的各项数据呈现由低到高再转低的趋势。

综合分析，当阈值大小在80左右，且范围较小时，有较好的增强效果。因此文中选取[σ_max=110]，[σ_min=40]作为[σ]阈值的最大值最小值。

4.2不同算法增强效果对比

图7是文中提出的算法与其他算法的图像处理结果。可以看出文中算法在局部细节和色彩恢复上表现得较为出色。相对文中算法，HE算法整体增强较好，但得到的图像普遍偏暗;ACE算法色彩恢复相对单一，局部细节欠佳：MSRCR的结果较差，总体亮度偏高。

表3、表4的为不同算法的评价数据，其中HE算法的均值普遍较低，导致图像整体亮度偏低;相对的MSRCR算法均值较高，但其他数据均较低，增强结果欠佳;ACE算法各项数据较为均衡。文中算法的均值在120左右，符合人眼视觉观察所需像素值标准，标准差、信息熵和平均梯度的数值表现良好。

6 结论

文中算法通过图像不同的景深差异来估计图像局部雾霾浓度，对不同浓度的雾霾场景进行自适应尺度的增强，很好地弥补了传统Retinex算法在固定尺度下只注重图像全局性增强的缺点。相对其他算法，文中算法的处理后的图像整体亮度较高，细节较好，具有良好的颜色恢复性，在提升了图像局部细节的同时，也兼顾了全局性增强。由于文中算法采取了自适应尺度对图像进行去雾增强，当尺度阈值范围较大时，子图融合后的图像边缘色差较大;当所有尺度阈值整体偏小时，图像的颜色恢复会出现一定的色彩失真现象。如何提高更好的自适应性是后面需要考虑的重点。

參考文献：

[1] 孙小明，孙俊喜，赵立荣，等.暗原色先验单幅图像去雾改进算法[J].中国图象图形学报，2014，19（3）：381-385.

[2] Kim J H，Jang W D，Sim J Y，et al.Optimized contrast enhancement for real-time image and video dehazing[J].Journal of Visual Communication and Image Representation，2013，24（3）：410-425.

[3] 谢凤英，汤萌，张蕊.基于Retinex的图像增强方法综述[J].数据采集与处理，2019，34（1）：1-11.

[4] Land E H，McCann J J.Lightness and retinex theory[J].Journal of the Optical Society of America，1971，61（1）：1.

[5] Jobson D J，Rahman Z，Woodell G A.Properties and performance of a center/surround retinex[J].IEEE Transactions on Image Processing，1997，6（3）：451-462.

[6] Rahman Z，Jobson D J，Woodell G A.Multi-scale retinex for color image enhancement[J].Proceedings of 3rd IEEE International Conference on Image Processing，1996，3：1003-1006.

[7] 汪荣贵，朱静，杨万挺，等.基于照度分割的局部多尺度Retinex算法[J].电子学报，2010，38（5）：1181-1186.

[8] He K M，Sun J，Tang X O.Single image haze removal using dark channel prior[C]//2009 IEEE Conference on Computer Vision and Pattern Recognition.June 20-25，2009，Miami，FL，USA.IEEE，2009：1956-1963.

[9] He K M，Sun J，Tang X O.Fast matting using large kernel matting Laplacian matrices[C]//2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.June 13-18，2010，San Francisco，CA，USA.IEEE，2010：2165-2172.

[10] Hartigan J A，Wong M A.Algorithm AS 136：a K-means clustering algorithm[J].Applied Statistics，1979，28（1）：100.

[11] 朱静.色彩恒常性理论及其在图像增强中应用研究[D].合肥：合肥工业大学，2011.

[12] 徐君，黄亚楼，李飞.K-Means聚类中序列模式和批量模式的比较研究[J].计算机科学，2004，31（6）：156-158，193.

[13] 袁雪庚，顾耀林.自动色彩均衡快速算法[J].计算机辅助设计与图形学学报，2005，17（10）：2269-2274.

【通联编辑：唐一东】