周期信号傅里叶级数分析演示系统设计

任亚莉

摘要：周期信号傅里叶级数分析教学中，内容繁多，画图困难，应用Matlab GUI设计了兩个演示系统。通过GUI界面，分析了八种对称性周期性信号与傅里叶级数系数关系以及典型周期矩形信号的时-频域特性，以交互的方式实现周期信号傅里叶级数分析动态演示仿真。系统将抽象的信号频谱内容直观化、可视化，激发学生学习兴趣，提高教学质量和效率。

关键词：信号与系统;傅里叶级数分析;动态模拟演示;Matlab GUI

中图分类号：TN911.6        文献标识码：A

文章编号：1009-3044（2020）28-0023-03

Abstract： In the teaching of Fourier series analysis of periodic signals， there are many contents and it is difficult to draw pictures. Two demonstration systems are designed by Matlab GUI. The relationship between eight symmetrical periodic signals and Fourier series coefficients and the time-frequency characteristics of typical periodic rectangular signals are analyzed through GUI interface. The dynamic demonstration simulation of Fourier series analysis of periodic signals is implemented in an interactive way. The abstract content is visualized and visualized. It stimulates students' interest in learning and improves the quality and efficiency of teaching.

Key words： Signals and systems; Fourier series analysis; Dynamic simulation demonstration; Matlab GUI

1 引言

《信号与系统》是高等院校通信、电子、计算机、自动化等专业的核心课程，其中很多概念和分析方法广泛应用于通信、自动控制、信号与信息处理、电路与系统等领域[1-2]。由于该课程物理概念抽象、理论性和数学性强，学生对其中的分析方法与基本理论不能很好地理解与掌握。因此，如何让学生更好地理解和掌握课程中的物理概念、基本原理、基本分析方法并灵活运用理论工具解决实际问题是该课程要解决的关键问题[3-4]。国内外高校相继应用Matlab GUI对该课程中的一些重点难点内容进行仿真和验证，并取得了较好的效果[5-7]。

周期信号的傅里叶级数分析中，建立信号时域波形与频谱之间的内在联系，理解不同信号频谱及其特点，是一个抽象的概念，是学习中的难点。如果周期信号的波形满足某些对称条件，其傅里叶级数中有些项将为零，不必计算这些零系数项，并且其余的计算公式也可简化。实际教学中理论内容多，图多，讲解效率低[8]。应用Matlab GUI[9]设计了“周期信号对称性与傅里叶级数系数关系分析系统”及“周期矩形信号时-频域分析动态模拟系统”，通过GUI直观界面来完成周期信号的傅里叶级数分析，避免了手工画图的烦琐，而且信号频谱变化、谐波特性、吉布斯现象、对称性与傅里叶级数系数关系等难点内容一目了然，更能轻松地理解周期信号频谱的特点与一般规律。

2 周期信号对称性与傅里叶级数系数关系分析系统

系统选择了八种对称性的典型周期性信号为例分析，信号参数均为：周期[T=1s]，角频率[ω=（2π）rad/s]，幅度为1V。

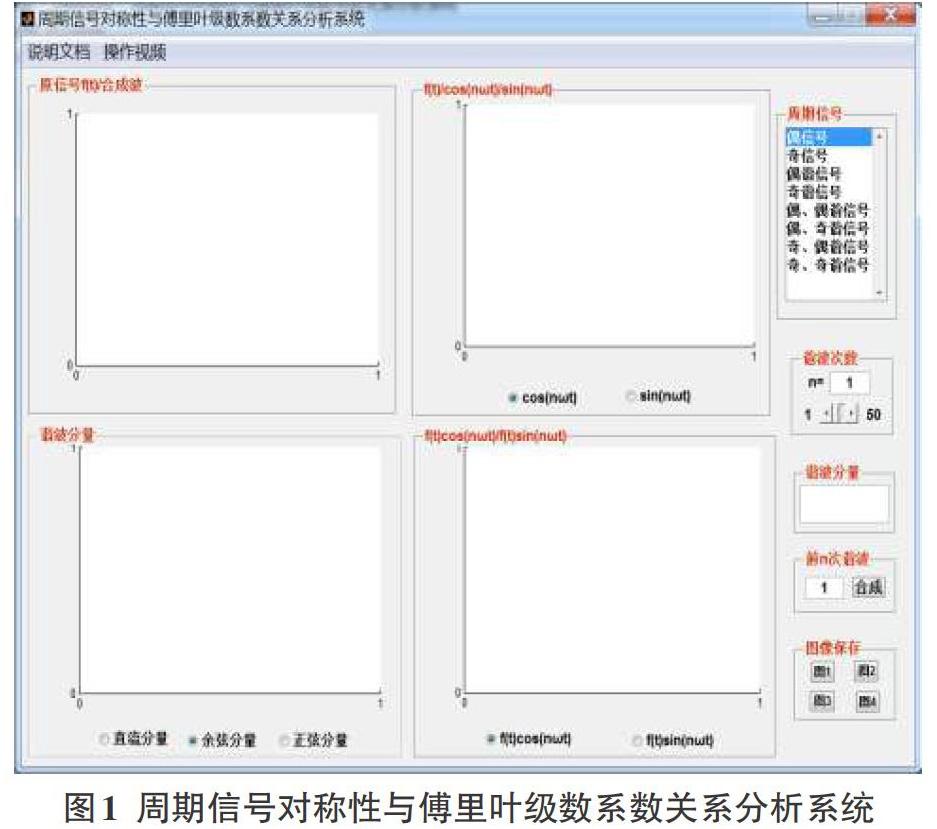
系统界面如图1所示，由七部分组成：（1）四个坐标区，显示周期信号[f（t）]、合成波、各次谐波、[cos（nωt）]、[sin（nωt）]、[f（t）cos（nωt）]及[f（t）sin（nωt）]波形图;（2）周期信号选择区，通过窗口界面右上角列表框任意选择信号;（3）谐波次数选择区，由窗口右“谐波次数”中滑动键控制，其值显示在对应的上方文本框中;（4）谐波分量数学表达式区，显示在窗口右“谐波分量”文本框中;（5）合成波谐波次数输入区，通过窗口右“前[n]谐波”中文本框输入;（6）图像保存区，由窗口左下角四个按钮组成，点击任何一个按钮会打开一个“图像保存”窗口，将对应四个坐标的图形以jpg形式保存在当前目录中;（7）菜单区，有“说明文档”和“操作视频”两个菜单。

系统主要功能：（1）八种对称性周期性信号（偶、奇、偶谐、奇谐、偶及偶谐、偶及奇谐、奇及偶谐、奇及奇谐）时域波形特点分析;（2）在[-T2]～[T2]区间内，绘制八种对称性周期性信号[f（t）]与[cos（nωt）]、[sin（nωt）]乘积波形图，通过观察它们的面积是否为零，从而方便判断对应的傅氏系数是否为零，其中[n]的范围为1～50;（3）绘制八种对称性周期性信号各次谐波分量波形，并给出对应的数学表达式;（4）绘制八种对称性周期性信号前任意[n]次谐波合成波波形。

观察奇谐信号对称性对傅氏系数的影响，奇谐信号波形特点是任意半个周期的波形可由它前面半个周期的波形沿横轴反折得到，即[f（t）=-f（t±T2）]。奇谐信号只含正、余弦波的奇次项，不含偶次项。选择列表框中的“奇谐信号”，当谐波次数n=1时，如图2所示，左上角坐标中给出了前1次谐波合成波波形，虚线表示，原周期信号用实线表示。

当谐波次数n=2时，如图3所示，左上角坐标中给出了前5次谐波合成波波形。

3 周期矩形信号时-频域分析动态模拟系统

系统以周期矩形信号为例，通过调整脉宽、周期及幅度各参数的大小，观察频域特性变化情况。

系统界面如图4所示，由四部分组成：（1）信号波形显示区，由四个坐标组成，分别动态模拟显示周期矩形信号、频谱信号、谐波信号及合成波信号波形;（2）参数改变区，位于窗口最下边，由文本框和滑动键组成，可调整信号脉宽、周期、幅度、谐波及视角等参数;（3）参数计算区，位于窗口最右边，由文本框组成，可计算信号内带宽分量、占空比、过冲值及方均根误差参数;（4）菜单区，有“说明文档”和“操作视频”两个菜单。

系统主要功能有：（1）周期矩形信号时-频对应关系动态模拟显示;（2）信號周期及脉宽变化对频谱的影响;（3）观察吉布斯现象;（4）通过视角变化，利用三维图形展示周期矩形信号的谐波特性;（5）信号带宽内分量、占空比、过冲值及方均根误差参数的计算;（6）当信号周期T→∞时，从傅里叶级数到傅里叶变换动态模拟显示。

在图4中，通过窗口下方的滑动键改变周期矩形信号任何一个参数时，“信号波形显示区”或“参数计算区”都会出现相应的动态变化。适当调整各参数，结果如图5所示。

4 结语

基于Matlab GUI功能设计的“周期信号傅里叶级数分析”动态演示系统，将抽象的傅里叶级数分析内容直观化，可视化，加深了学生对内容的理解与掌握，激发学习，具有很好的参考和应用价值。系统窗口界面大方，功能齐全，控制精细，既可在课堂上理论讲解演示，也可用于实验教学，或提供给学生自主操作学习，教师进行答疑与辅导。为确保系统正常运行，“前n谐波”文本框中要求输入正整数，如果输入字符、负数或空格等会出现“输入任意正整数！”信息提示。为了使系统适应不同类型的显示器，应用屏幕适应性算法，程序运行后，其窗口界面及控件的大小和比例会保持不变。

为方便学生学习，系统提供了说明文档和操作视频。说明文档是Word文档，详细说明了系统设计的思路方法、组成结构、实现的功能及详细操作方法等;操作视频是mp4文件，配有语音和字幕，简单演示了该系统的操作方法，可使学生快速掌握该系统的操作。学生在使用学习的过程中，可提出自己的修改意见，使系统不断得到完善和补充，让学生切实感受到可视化教学过程，积极参与教学过程，从灌输课堂向对话课堂转变。

参考文献：

[1] 胡沁春.信号与系统[M]. 重庆：重庆大学出版社，2015.

[2] 胡光锐，徐昌庆.信号与系统[M]. 上海：上海交通大学出版社，2013.

[3] 韩连福，王海霞，付长凤，等.信号与系统课程教学改革与实践探索[J]. 当代教育实践与教学究，2019（2）：52-53.

[4] 王琼，欧阳征标，刘强.《信号与系统》课程中以实用设计为导向的实验教学探讨[J]. 信息系统工程，2019（12）：168-170.

[5] 冯英翘，宋超，黄晓红，等.面向专业应用型人才培养的信号与系统课程改革[J].华北理工大学学报（社会科学版），2020，20（2）：85-88+126.

[6] 赵伶俐.新工科背景下信号与系统课程实践教学改革研究[J]. 中国教育技术装备，2019（18）：119-120+124.

[7] 程正梅，刘云连，付又香.基于MatlabGUI的“信号与系统实验”仿真平台搭建研究[J]. 电脑知识与技术，2019，15（12）：236-237.

[8] 陈后金，胡健，陶丹，等.“信号与系统”慕课建设[J]. 南京：电气电子教学学报，2018，40（1）：29-31.

[9] 蒋珉.Matlab程序设计及应用[M]. 北京：北京邮电大学出版社，2015.

【通联编辑：王力】