车桥耦合振动2019年度研究进展

李小珍 辛莉峰 王铭 傅沛瑶 王党雄 晋智斌 朱艳

摘 要：车辆运行于桥梁上，车辆与桥梁之间相互作用、相互影响，称为车桥耦合振动。车桥耦合振动理论为桥梁设计、线路运营、维护及管理提供了理论基础、分析方法和评估手段，具有重要的工程应用价值。自20世纪起，众多学者已经开展了大量卓有成效的研究工作。近年来，中国交通运输行业飞速发展，稠密的交通网、紧张的运能、复杂的线路条件等因素对传统的车桥耦合振动理论提出了新的挑战，也催生了相关先进理论技术的发展。为了促进该领域后续更加全面深入的基础研究，对轨道不平顺作用下的车桥耦合振动、轨道不平顺作用下的车桥耦合随机振动、风车桥耦合振动、地震車桥耦合振动、磁浮交通车辆轨道梁耦合振动等5个方面在2019年的研究进展进行了总结，并对研究热点和展望进行了梳理。

关键词：车桥耦合振动;车桥耦合随机振动;风车桥耦合振动;地震车桥耦合振动;磁浮交通车辆轨道梁耦合振动

中图分类号：U441.3   文献标志码：A   文章编号：2096-6717（2020）05-0126-13

收稿日期：2020-04-23

基金项目：国家自然科学基金（51878565、U1434205）

作者简介：李小珍（1970- ），男，教授，博士生导师，主要从事车-桥耦合动力学研究，E-mail： xzhli@swjtu.cn。

朱艳（通信作者），女，博士，E-mail： zhuyan@swjtu.cn。

Received：2020-04-23

Foundation items：National Natural Science Foundation of China （No. 51878565， U1434205）

Author brief：Li Xiaozhen（1970- ）， professor， doctorial supervisor， main research interest： vehicle-bridge interactions， E-mail： xzhli@swjtu.cn.

Zhu Yan （corresponding author）， PhD， E-mail： zhuyan@swjtu.cn.

Abstract： When a vehicle runs on a bridge， the vehicle and the bridge will be mutually influenced in the dynamic behavior， which is called vehicle-bridge interactions. The vehicle-bridge coupled vibration theory can provide the theoretical basis， analysis method and assessment technique for bridge design， line operation， maintenance and management， and it is of important engineering application value. Many scholars have carried out a lot of relevant researches since the 20th century. At present， Chinas transportation industry has developed rapidly. Conventional vehicle-bridge interaction dynamics are challenged by the dense transportation network， tight transportation capacity， complicated line conditions， etc. Thus， the related theory and technique are being and further developed. This paper summarizes the progress and advances of the vehicle-bridge interaction field in 2019， including the vehicle-bridge interaction model under track irregularity， vehicle-bridge random vibrations under track irregularity， wind-vehicle-bridge coupled vibrations， earthquake-vehicle-bridge coupled vibrations， and maglev vehicle-bridge coupled vibrations. Furthermore， the research hotspots and prospects are provided. The work is expected to promote more comprehensive and in-depth basis researches.

Keywords：vehicle-bridge interactions; vehicle-bridge random dynamics; wind-vehicle-bridge interactions; earthquake-vehicle-bridge interactions; maglev vehicle-bridge interactions.

近年来，中国铁路、公路、轨道交通领域桥梁建设事业蓬勃发展，成就举世瞩目。在众多的桥梁系统工程力学问题中，车桥耦合动力学问题是一个历久弥新的研究课题，涉及车辆动力学、轨道动力学、结构动力学、轮轨接触力学以及数值分析等多个研究方向，属于多学科交叉的复杂问题，其研究的核心目标通常为如何准确地预测在实际复杂运营条件下车桥耦合系统的动力响应，进而优化结构设计及建造，并对铁路、公路系统养护及维修做出指导。因此，开展车桥动力相互作用研究极其重要，一直是交通运输领域的研究热点之一，尤其是20世纪八九十年代以来，中国学者已经开展了大量卓有成效的研究工作。当前，中国铁路、公路、轨道交通领域的桥梁建设面临高速度、大运载量、高舒适度等新的挑战，车桥耦合振动研究在新形势下催生出新的研究热点和发展趋势。

为了推动车桥耦合领域更加全面、深入的基础研究，促进该课题在实际工程中的推广及应用，更进一步地对规模庞大的桥梁工程进行科学经济地维护和管理，笔者总结了2019年度轨道不平顺下的车桥耦合振动、车桥耦合随机振动、风车桥耦合振动、地震车桥耦合振动、磁浮交通车辆轨道梁耦合振动等5个方面的研究进展，并对研究热点进行了展望。

1 轨道不平顺作用下的车桥耦合振动研究

以轨道不平顺作为主要激励源的车桥耦合分析模型是整个复杂外界环境激励下车橋耦合振动理论的前提及基础。纵观其漫长的发展史[1-2]，车辆模型、轨道模型、桥梁模型、轮轨接触关系等各部分的建模方法与理论已逐步趋于完备且一致：车辆结构多基于多刚体动力学建模，轨道及桥梁结构采用有限元方法建模，轮轨接触主要以轮轨密贴刚性接触理论和Hertz弹性接触理论及Kalker蠕滑理论作为代表，数值积分方法以Newmark-β方法、Zhai方法、Runge-Kutta方法、Houbolt方法等为主。这些理论在保证计算效率的同时较为准确地预测了系统中、低频的动力响应。近年来，面向不同的工程实际需求，车桥耦合振动理论在精细化、精简化、实用化、理论解析、反问题、智能化、可视化等方面继续拓展及深入。

1.1 精细化模型

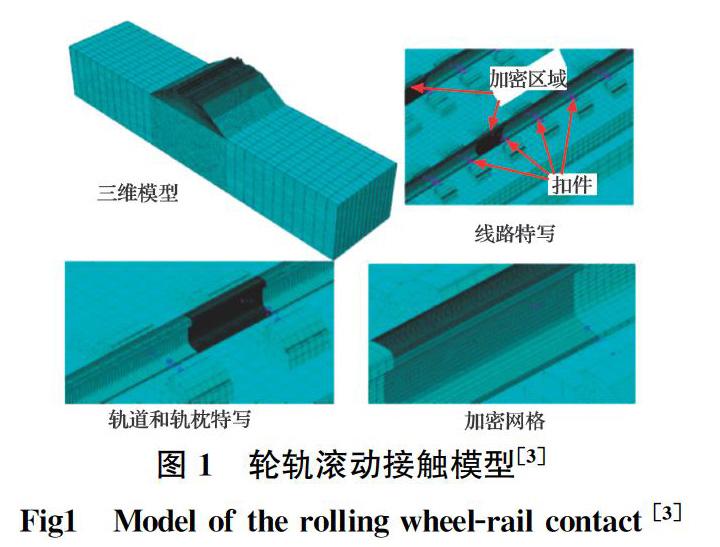
常规车桥耦合模型有时不能精准地反映工程中子构件的局部动力行为或机理，因此，根据所要揭示的特殊问题，需将车桥耦合动力分析模型精细化，如：Xue[3]建立了车轮-轨道轨下基础系统中的轮轨滚动接触模型（图1），模拟了车轮从静止加速到以预期速度向前滚动的过程，分析了滚动轮轨接触在期望速度下的动力特性;张经纬等[4]基于经典半空间10自由度车桥耦合动力模型，运用集中质量法引用动态单元法，建立了考虑轮轨接触损失的半空间13自由度人车线耦合动力模型，厘清了轮轨接触损失条件下列车乘员舒适性的差异;Gou等[5]理论推导了轨道位移和桥梁位移之间的映射关系，以此为基础，研究了桥墩沉降对车桥耦合系统动力响应的影响，并提出了不同车速下的桥墩沉降设计安全阈值，对实际桥梁工程建设具有较大的指导意义;昌超等[6]应用多体动力学软件UM、有限元软件ANSYS、前处理软件HYPERMESH，将轨道、桥梁系统考虑为柔性体，轮轨接触设定为轮轨非椭圆多点接触，建立三维车线桥耦合动力学精细模型，重点研究了车轮型面磨耗对高速铁路无砟轨道、桥梁振动特性的影响。此外，孙宇[7]在车轨耦合动力学中提出了一种新的轮轨非赫兹接触算法MKP法，方法具有很好的计算精度、计算稳定性和计算效率，适合于实时的轮轨动力相互作用计算，对于车桥耦合系统轮轨接触的模拟同样具有指导意义。

1.2 简化模型及高效算法研究

车桥耦合模型具有时间、空间双重非线性特征，计算负荷大、时间久，不利于与实际工程迅速对接。模型中妨碍计算效率的主要因素：以Hertz理论为主导的轮轨接触理论所导致的时间积分步长过小、庞大自由度的轨道系统、分离式建模引发的迭代问题等。因此，Xu等[8]基于车辆轨道耦合动力学理论和能量变分法，以刚性接触方式考虑轮轨脱离或者未脱离时的轮轨位移和力素协调条件，以矩阵耦合形式建立列车轨道桥梁系统动力学时变统一方程。黄博等[9]基于车桥系统内在机理和等效粘滞阻尼的思想，提出在移动集中力模型中加入附加阻尼即可用于评估车桥耦合模型下桥梁的动力响应。Zhu等[10]提出了车桥耦合模型的异步长多软件联合仿真方法，车轨系统采用了显式积分法，并应用了移动轨道技术来进一步提升模型的计算效率。Jin等[11]应用Ritz法处理钢轨方程，减少了钢轨自由度达80%。Jin等[12]提出了一种统计线性化方法处理车轨桥模型里最为复杂的轮轨关系，极大地提高了计算效率。Zeng等[13]采用拉氏乘子法处理轮轨关系，以提高轮轨接触关系的计算效率。Zhu等[14]在虚拟激励法中引入自适应积分选点，提高了车桥随机分析的效率。Li等[15]联合Ansys和Simpack软件，通过轮轨位移协调条件和相互作用力平衡条件联系车辆和桥梁子系统，使模型利于工程实际的对接。整体而言，车桥耦合简化模型或者高效算法仍会落足于轨道简化、轮轨接触简化、高效积分算法、统一化建模等方面。

1.3 相互作用的解析理论

不同于数值方法，车桥耦合相互作用理论的解析解可以直观地观测每个因素所起的影响及作用，如最为典型的车致桥梁共振理论。近年来，研究者从不同角度给出了桥梁附加阻尼公式[16]，包括频响等效、耗能等效，来考虑车辆对桥梁的减振作用。UIC规程给出了折减系数拟合曲线用于轨道对桥梁的减振作用。Jin等[17]推导出了轨道对桥梁减振系数的解析公式，将轨下荷载分布函数作傅氏变换，取桥梁频率与车速比值处的值。关于车辆通过梁端转角时的轮重减载率，Jin等[11]也提供了相应的解析公式。由于理论解析解需要大量的公式推导，发展速度较为缓慢，主要作用在于识别关键参数或提供更为简单的数值曲线用于数值分析使用。

1.4 系统反问题相关理论研究

车桥耦合系统反问题，涉及荷载识别和系统参数辨识，通过测试车桥系统动力响应，建立相关理论与模型来反推系统本身物理参数。近期主要进展包括：Deng等[18]采用等效剪力法根据测试的桥梁响应来识别车辆荷载;Tan等[19]用车辆响应测试量反演桥梁频率及模态;Yang等[20]根据实测车辆响应对桥梁模态和桥梁损伤进行识别。Ticona Melo等[21]利用遗传算法从非常有限的桥梁实测数据中提取了模态参数，研究了考虑车辆轨道结构相互作用的钢混凝土组合铁路桥梁数值模型的标定与验证。车桥耦合系统反问题的研究成果对桥上车辆运营管理、桥梁损伤识别、桥梁养护维修等具有重要的指导意义，在未来几年内，该领域将在结合信号处理技术和模态分析理论的基础之上，进一步提高识别能力，并应用如全局敏感度分析理论的随机分析方法识别敏感参数，提高反问题识别过程中的效率性及精确度。

1.5 面向桥梁运营管理的数字化分析系统

目前，车桥耦合系统的数值模拟多数侧重于桥梁设计阶段，针对成桥阶段桥梁在风荷载、随机车流、温度等运营荷载作用下的动力仿真较少，谢青等[22]、Yuan等[23]研发了桥梁动力分析软件BDANS，软件具有“从平面到空间，从静力到动力，从确定到随机”的显著特点，推进了车桥耦合动力仿真软件在三维可视化、智能化、数字化等方面的进步，对形成桥梁智能养护维修关键技术体系与现代化管养策略有重要指导意义，仍需进一步研究。

2 轨道不平顺作用下的车桥耦合随机振动研究

受自然环境等多种不确定因素的影响，车桥耦合系统本身结构参数、外部激励等均具有明显随机性特征。仅仅考虑物理力学参数不变的设计值及确定性外荷载的动力分析结果，是车桥耦合时空间随机场的一次体现，不能准确反映车桥耦合系统真实动力学状态。鉴于此，从随机角度来揭示车桥耦合随机系统的内在机理及规律，是近年来研究热点，且取得了较为丰硕的成果。

2.1 车桥耦合系统随机振动理论和分析方法

精确、快速、适用于车桥耦合动力学系统的随机数学方法是当前车桥耦合随机动力学发展的集中突破点。Jiang等[24]采用了新点估计法研究了桥梁各种不确定因素作用下车桥耦合系统随机响应，随机因子主要包括桥梁材料参数、环境因素及预应力参数，证明了新点估计法较传统蒙特卡洛方法可提高2～3个数量级的计算效率。Han等[25]提出了一种基于非线性自回归的外源性输入人工神经网络模型的代理建模方法提高列车桥梁耦合随机分析的效率，并论证了其方法中重要样本的关键性。向活跃等[26]采用了子集分裂模拟方法对车桥耦合系统的极值响应进行了统计，得到了车辆极值响应的超越概率曲线，并与直接蒙特卡洛方法進行了对比验证，证明其方法可大幅减少计算样本。目前，针对车桥耦合随机动力分析的数学方法仍然较少，是发展重点之一。

2.2 列车桥梁耦合系统响应的不确定度

量化由于激励源、系统参数的空间非定常特征导致的车桥耦合动力响应的不确定是当前车桥耦合随机分析领域的另一大重点[24-26]。Mao等[27]利用概率密度演化法探索了多种随机激励下重载铁路中列车桥梁耦合系统的动力响应上下界问题，并基于朔黄重载铁路32 m简支梁桥现场试验验证了方法及所采用的输入参数概率分布的合理性。Xin等[28]从随机角度探讨了铁路列车导致的桥梁共振问题，定义及阐释了“随机共振”及“随机消振”现象，结合Nataf变换理论分析了变量间的概率相关性对共振及消振车速概率分布特征的影响，并研究了“随机共振”现象对车桥耦合系统随机动力响应的影响规律。Xiao等[29]利用概率密度演化方法研究了轨道不平顺激励下车线桥耦合系统的随机响应，得到了众多有意义的结论。

2.3 列车桥梁耦合系统敏感因子识别

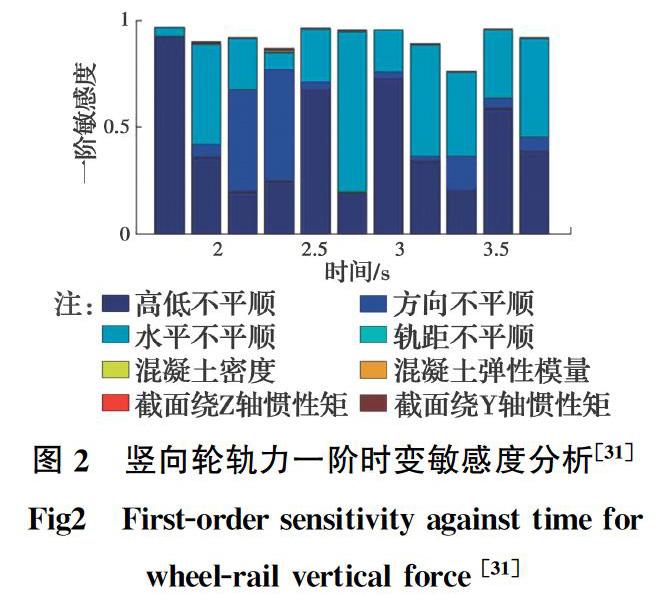
敏感度问题主要探究众多的随机因子中到底哪些对车桥耦合随机响应影响较大，用于在实际工程设计及建设中做出指导、重点把控。Wan等[30]结合Sobol敏感度理论和高斯过程模型，分析了某二维车桥耦合模型的全局敏感度，通过与蒙特卡洛方法对比，验证了方法的正确性;Xin等[31]采用概率密度演化方法探明了轨道随机不平顺和系统随机参数导致的车桥耦合系统动力响应不确定性，并基于推广的傅里叶幅度敏感度检验法，考虑输入参数的实际概率分布，且允许所有参数同时变化，定量分析了各参数及参数之间的相互作用对随机系统响应的影响，对各动力指标的关键影响因素进行了排序，如图2所示。

2.4 列车桥梁耦合系统动力可靠度

结构动力可靠度是结构动力学重要分支，它研究结构承受随机动载荷时不发生失效破坏的概率。李小珍等[32]发展了一种包含谱概率、幅值、波长、相位等信息的全概率轨道不平顺模型，引入概率密度演化方法，量化了系统各动力指标的时变统计矩和可靠度，研究方法可用于大规模铁路线路车桥耦合系统的动力可靠度评估。Jin等[33]采用析因试验设计方法提取对重载列车弯桥耦合随机系统中动力响应敏感的随机参数，应用响应面法明确各敏感随机参数对系统失效概率的影响，进而量化曲线地段轨道桥梁结构的可靠度。

3 风车桥耦合振动研究

随着经济社会的快速发展、互联互通需求的剧增，桥梁工程不断从内陆向近海延伸，逐渐复杂的风场环境使得大跨桥梁的行车安全性和平稳性受到了更为严峻的考验[34]。近年来，风车桥耦合振动的研究取得积极进展，从车桥系统气动参数研究、挡风措施及机理研究、车桥系统行车抗风安全性评估和风浪/流车桥耦合振动研究等几个方面进行回顾。

3.1 车桥系统风荷载

列车桥梁系统气动参数测试及脉动风场模拟直接关系到风车桥耦合系统的输入风荷载，同时，由于风荷载突变效应是风车桥系统的控制性因素之一，也是近来车桥系统风荷载研究的一个主要方面。

为提高针对大跨度桥梁非均匀脉动风场模拟的效率，李永乐等[35]提出了一种新颖的Cholesky分解法;王浩等[36]基于非负矩阵分解，对大跨度桥梁开展了非平稳风场的模拟研究;靖洪淼等[37]采用数值模拟方法分析了山区峡谷桥址处的风场特性，实现了高质量的山区风场数值模拟及解决了数值计算雷诺数与实际不符的难题;徐曼等[38]基于实测数据的风速谱采用谐波合成法模拟得到了沪通公铁两用长江大桥的三维脉动风速场。

针对高速列车驶经复杂环境时所出现的风荷载突变效应，何佳骏等[39]采用数值模拟方法分析了桥隧过渡段列车气动特性的变化，研究发现车头位置会呈现出更为明显的气动特性突变;李小珍等[40]采用桥上移动列车测试系统测试了桥塔遮蔽效应对列车气动特性的影响，如图3所示，研究表明车辆气动参数在桥塔区域会呈现出明显的突变现象。

大跨桥梁结构整体趋于细长、轻柔，其静风力作用和脉动风作用下的响应更为突出。刘昊苏等[41]采用风洞试验与计算流体力学相结合的方法，对常用公铁两用斜拉桥双层桁架主梁静三分力系数进行研究，分析了雷诺数的影响，并提出了高风攻角下识别三分力系数最低雷诺数的建议值;Ma等[42]和Li等[43]针对典型流线型箱梁断面进行了二维及三维气动导纳系数的风洞试验研究（图4），并提出了气动导纳的识别方法。

3.2 挡风措施及机理研究

风屏障的正确布置及合理选型对改善桥上列车复杂行车风环境极为重要，风屏障的研究通常集中于选型、布置高度及透风率等方面。Xiang等[44]通过风洞试验测试了不同高度风屏障的防风效果，同时桥上移动车辆测试装置的采用可以更为真实地反映风屏障的防风性能;Ren等[45]和He等[46]则通过分析风屏障前后及列车周围流场特性的发展来研究风屏障类型、透风率对风屏障的防风性能影响。

3.3 车桥系统行车抗风安全性评估

高速列车的行车安全性评估需通过风车桥耦合系统来综合考虑横风、列车、桥梁三者之间的相互影响。韩艳等[47]结合有限元软件ANSYS和多体动力学软件SIMPACK建立列车轨道桥梁三维多体系统模型，研究了非定常气动力荷载对列车行驶安全的影响;He等[48]提出一种基于伪激励法的非平稳风载车桥耦合振动分析框架，进行了非平稳风对车桥系统性能影响的研究;Guo等[49]研究了风屏障对风车桥耦合系统中车辆动力性能的优化效果;李小珍等[50]开展了侧风作用下五峰山长江大桥列车行车安全控制研究，通过数值模拟给出了五峰山长江大桥在各风速下保证行车安全的车速阈值。

3.4 风浪/流车桥耦合振动研究

海洋环境中的桥梁工程同时受强风、巨浪、急流等复杂荷载的作用，准确建立各类荷载模型对进行风浪/流车桥耦合振动研究起到至关重要的作用。刘高等[51]通过现场同步连续观测获得了风浪流耦合场观测数据，并将其置于风车桥耦合系统，分析车辆在极端条件的行车安全性及稳定性。李永乐等[52]建立了波浪风列车桥梁动力模型，将风场视为空间相关的平稳高斯过程，并将波浪作为外部荷载施加到該耦合体系中，分析了波高、风速、车速对耦合模型车辆和桥梁响应的影响;魏凯等[53-54]先后采用叠加风场和TPXO潮汐模式共同驱动的SWAN+ADCIRC波流耦合模式模拟台风期间近岸海域波浪风暴潮的生成与发展过程，运用ANN算法中常用的BP神经网络对外海海洋预报台提供的波高、风速数据以及在桥址区实测波高数据进行训练，建立二者之间的映射关系及ANN推算模型。

4 地震车桥耦合振动研究

中国地处环太平洋地震带和亚欧地震带之间，地震断裂带数量多，地震频发，多而密的高铁路线不可避免地会穿越活跃地震断裂带，高速列车行车时遭遇地震的概率大幅提高，地震作用下桥上高速列车行车安全研究十分必要。目前，学者们对地震车桥耦合体系的研究主要集中在系统地震动激励、地震车桥耦合振动模型、行车安全性评估以及振动台试验研究等方面。

4.1 系统地震动激励

视震源机制、场地条件、传播路径等因素不同，地震动自身具有非常大的随机性。以往地震车桥的相关研究中，以近场地震、远场常规地震、非一致地震激励、三维地震激励等多种地震波作为系统激励源，如Chen等[55]分别考虑近断层脉冲、非脉冲和远场地震动对车桥系统动力响应的影响，并指出脉冲地震波对列车的行车安全影响更大;沈毓婷[56]分别考虑具有方向性和滑冲效应的实测近断层地震波以及人工合成的脉冲地震波，研究了近断层地震波对无砟轨道结构和列车行车安全性的影响;研究仍在继续深入，如乔宏等[57]基于粘弹性边界理论建立考虑地形和地震波入射角影响的局部场地模型，获取场地地震动时程，分析了山区地形和地震动斜入射角对车桥系统地震响应的影响。

4.2 地震车桥耦合振动精细化模型

地震车桥耦合振动模型是车桥耦合动力分析模型的进一步延伸[58]。国巍等[59]基于Simpack和OpenSees软件开发了车轨桥系统联合仿真程序，建立了强震下车轨桥系统精细化模型，考虑结构参数在强震作用下的非线性情况，分析了地震和轨道不平顺激励下列车的运行安全性;Zeng等[60]考虑轮轨两点接触、单点接触和分离的情况，建立了模拟不同轮轨接触状态的地震车桥分析模型，并基于脱轨系数和轮重减载率评价了列车的行车安全;Borjigin等[61]提出了一种同时考虑车辆动荷载和地震作用的车桥耦合系统动力响应分析方法，研究了两种荷载作用下系统的动力响应特点，指出了地震作用下忽略车辆荷载可能会低估结构的地震响应。

4.3 车桥系统行车抗震安全性评估

目前，地震作用下车桥系统的抗震安全性受到了学者的广泛关注[62-63]，研究采用数值分析方法对高速列车地震安全性、平稳性以及桥梁动力响应对行车安全的影响进行研究，如图5所示[62]。Wei等[64]研究了地震动不确定特征周期对车桥系统地震响应和地震易损性的影响，结果表明，桥梁和轨道部件易损性随地震动特征周期增加，采用恒定特征周期的地震动可能导致不安全的结果;雷虎军等[65]采用自编程序TTBSAS研究了钢筋混凝土拱桥的地震响应，给出了CRH3高速列车安全通过该桥时地震动的速度阈值。此外，地震作用下车桥耦合系统的预警研究开始兴起，目前的相关研究主要集中在利用车桥模型进行振动台试验，探讨传统脱轨指标的局限性，提出采用轮轨水平相对位移、车轮抬升量和车体倾覆角等位移指标对地震作用下列车的地震预警阈值进行评价[66]。

4.4 地震车桥实验室模型及试验研究

传统数值模拟方法对地震作用下车桥系统的安全性有了初步的认识和研究，提出了具体的行车安全评价指标，但其值偏于保守，应用于实际工程可能导致偏于不安全的结果。为确保车桥系统地震预警阈值的准确性和可靠性，相应的振动台试验应运而生。利用振动台试验，研究者可以精准捕捉地震作用下列车的脱轨行为，掌握脱轨机理，提出更加准确可靠和行之有效的地震预警阈值。目前，相关的试验研究较少，主要集中在日本等少数国家，中国车桥系统的振动台试验研究尚处于起步阶段，北京交通大学做了一些初步的尝试和研究，如图6所示。李昊等[67]通过准静态全尺寸车辆轨道模型振动台试验发现，规范所给轮重减载率和脱轨系数限值偏于保守，且列车实际脱轨行为与传统数值研究有异，并给出了基于实验的高速列车地震预警阈值。

5 磁浮交通车辆轨道梁耦合振动研究

随着磁浮交通的发展，磁浮车辆轨道梁耦合振动问题也成为了当前的研究热点之一。磁浮列车通过摒弃传统的轮轨接触，利用电磁悬浮力将车体悬浮在额定悬浮间隙附近（图7所示），从而具有爬坡能力大、转弯半径小、低振动、低噪声、污染小等优点，日益受到人们的青睐。这一新型接触方式的使用，使得磁浮车桥耦合振动的问题更加突出，诸多试验线路或运营线路均由于强烈的磁浮车桥耦合振动而导致磁浮列车无法平稳运行，韩国的仁川机场中低速磁浮线路由于强烈的车桥耦合振动导致计划运营时间一拖再拖。因此，磁浮交通车桥耦合振动研究十分必要。近期研究进展主要集中在新型磁浮列车研发、主动悬浮控制系统改进和磁浮车桥耦合振动理论和方法。

6 研究热点与展望

中国铁路、公路、轨道交通桥梁工程建设取得了巨大成就，但桥梁工程也将面临严峻的新形势，如中西部极端恶劣气候条件下的桥梁建设;大跨度跨河、跨海桥梁的设计;大规模的既有桥梁将步入长时效安全管理与维护阶段;自然灾害条件下桥梁的运营预警等。因此，未来10～20年，桥梁车致振动研究将面临创新、转型、升级的重要战略机遇期，研究应注重支撑性、前瞻性、系统性和交叉性，从顶层设计视角致力于全面解决这些建设及运维过程中的核心关键难题。以下几个方面的研究是下一阶段的研究热点：

1） 既有以轨道不平顺作为激励源的车桥耦合振动理论与模型已经较为完善，能在保证计算效率的同时较为准确地预测了系统中低频的动力响应。展望未来，车桥耦合模型仍会在精细化、实用化、理论解析、反问题、智能化、可视化等当前研究热点下继续向数字化发展，实现基础设施运行感知立体化智能化、评估预警维养系统化、运维业务数据标准化等基础理论的创新和关键技术的突破。

2） 车桥耦合随机动力学理论研究尚不充分，近期热点在于提高随机分析计算效率的数学方法、响应的不确定度量化、敏感因子识别、动力可靠度等方面。为实现基于可靠度的车桥耦合设计理念，车桥耦合随机分析不仅应当继续在当前热点上继续深入研究，还应进一步就耦合系统长时效演化规律、复杂激励下耦合系统的随机动力内在机理探索、车桥耦合随机动力学的实际应用问题等方面纵向展开。

3） 风车桥耦合振动近期研究热点主要在于：开发高车速、小偏角、大攻角等条件下桥上移动车辆模型风洞试验技术;基于可靠度分析理论，建立考虑系统随机性和激励随机性的风车桥系统可靠度分析方法;风浪联合作用下大跨度桥梁车桥耦合振动。目前，研究多数仅为在数值模拟，可进一步开展结构风、浪、流的耦合作用模型试验，为数值结果及工程实际提供参照。

4） 地震车桥相关研究主要围绕车辆及桥梁的动力响应分析和高速列车的行车安全性评估展开，由于核心试验的缺失，理论尚未得到可靠的验证。预期在未来数年内，地震列车桥梁耦合振动理论将围绕地震车桥耦合振动模型的进一步开发及相应的振动台试验验证、从地震预警阈值的角度对地震列车桥梁耦合系统行车安全评价指标进行丰富和完善、基于概率的行车安全可靠度等课题展开。

5） 厘清真实的磁浮交通车轨桥耦合振动机理是磁浮交通进一步发展的瓶颈。面向未来新一代时速600 km甚至更高速度的高速磁浮交通，建立基于智能主动反馈控制磁轨关系的磁浮交通车轨桥系统精细化模型，研究制定高速磁浮交通设计标准，对磁浮交通工程动力安全性及工程经济性具有重要意义。同时，针对云轨、智轨、空铁等新型轨道交通制式，开展相应车桥耦合振动研究，具有同样重要的理论意义和工程价值。参考文献：

[1] 李小珍， 强士中. 列车桥梁耦合振动研究的现状与发展趋势[J]. 铁道学报， 2002， 24（5）： 112-120.

LI X Z， QIANG S Z. State-of-the-art review and trend of studies on vehicle-bridge interaction [J]. Journal of the China Railway Society， 2002， 24（5）： 112-120.（in Chinese）

[2] ZHAI W M， HAN Z L， CHEN Z W， et al. Train-track-bridge dynamic interaction： A state-of-the-art review [J]. Vehicle System Dynamics， 2019， 57（7）： 984-1027.

[3] XUE F C. Investigation of rolling wheel-rail contact using an elaborate numerical simulation [J]. Proceedings of the Institution of Mechanical Engineers， Part F： Journal of Rail and Rapid Transit， 2020， 234（10）： 1198-1209.

[4] 張经纬， 刘学文， 王岩松， 等. 考虑轮轨接触损失的列车乘员舒适性分析[J]. 振动与冲击， 2019， 38（16）： 181-187， 207.

ZHANG J W， LIU X W， WANG Y S， et al. Riding comfort of trains with rail irregularities considering contact loss of wheel-rail [J]. Journal of Vibration and Shock， 2019， 38（16）： 181-187， 207. （in Chinese）

[5] GOU H Y， YANG L C， MO Z X， et al. Effect of long-term bridge deformations on safe operation of high-speed railway and vibration of vehicle-bridge coupled system [J]. International Journal of Structural Stability and Dynamics， 2019， 19（9）： 1950111.

[6] 昌超， 肖乾， 王亞朋. 高速列车车轮型面磨耗对轨道、桥梁振动特性影响分析[J]. 振动与冲击， 2019， 38（13）： 185-196.

CHANG C， XIAO Q， WANG Y P. Effects of high-speed trains wheel wear on vibration characteristics of track and bridge [J]. Journal of Vibration and Shock， 2019， 38（13）： 185-196. （in Chinese）

[7] 孙宇. 轮轨非Hertz接触方法及其在高速铁路轮轨动力相互作用中的应用研究[D]. 成都： 西南交通大学， 2018.

SUN Y. Wheel-rail non-Hertzian contact method and its application in the study of wheel-rail dynamic interaction on high-speed railway [D]. Chengdu： Southwest Jiaotong University， 2018. （in Chinese）

[8] XU L， ZHAI W M. A three-dimensional model for train-track-bridge dynamic interactions with hypothesis of wheel-rail rigid contact [J]. Mechanical Systems and Signal Processing， 2019， 132： 471-489.

[9] 黄博. 车线桥竖向振动等代解耦研究[D]. 成都： 西南交通大学， 2019.

HUANG B. Study on the decoupling of train-track-bridge system vertical vibration [D]. Chengdu： Southwest Jiaotong University， 2019. （in Chinese）

[10] ZHU Z H， GONG W， WANG L D， et al. Efficient assessment of 3D train-track-bridge interaction combining multi-time-step method and moving track technique [J]. Engineering Structures， 2019， 183： 290-302.

[11] JIN Z B， YUAN L G， PEI S L. Efficient evaluation of bridge deformation for running safety of railway vehicles using simplified models [J]. Advances in Structural Engineering， 2020， 23（3）： 454-467.

[12] JIN Z B， PEI S L， LI X Z， et al. Probabilistic evaluation approach for nonlinear vehicle-bridge dynamic performances [J]. Journal of Sound and Vibration， 2015， 339： 143-156.

[13] ZENG Q， STOURA C D， DIMITRAKOPOULOS E G. A localized Lagrange multipliers approach for the problem of vehicle-bridge-interaction [J]. Engineering Structures， 2018， 168： 82-92.

[14] ZHU S Y， LI Y L， TOGBENOU K， et al. An efficient optimization algorithm to study the stochastic responses of vehicle-bridge coupling systems [J]. Computing in Science & Engineering， 2019， 21（3）： 6-17.

[15] LI Y L， XU X Y， ZHOU Y， et al. An interactive method for the analysis of the simulation of vehicle-bridge coupling vibration using ANSYS and SIMPACK [J]. Proceedings of the Institution of Mechanical Engineers， Part F： Journal of Rail and Rapid Transit， 2018， 232（3）： 663-679.

[16] YAU J D， MARTíNEZ-RODRIGO M D， DOMNECH A. An equivalent additional damping approach to assess vehicle-bridge interaction for train-induced vibration of short-span railway bridges [J]. Engineering Structures， 2019， 188： 469-479.

[17] JIN Z B， HUANG B， REN J J， et al. Reduction of vehicle-induced vibration of railway bridges due to distribution of axle loads through track [J]. Shock and Vibration， 2018， 2018： 1-14.

[18] DENG L， HE W， YU Y， et al. Equivalent shear force method for detecting the speed and axles of moving vehicles on bridges [J]. Journal of Bridge Engineering， 2018， 23（8）： 04018057.

[19] TAN C J， UDDIN N， OBRIEN E J， et al. Extraction of bridge modal parameters using passing vehicle response [J]. Journal of Bridge Engineering， 2019， 24（9）： 04019087.

[20] YANG Y B， ZHANG B， CHEN Y N， et al. Bridge damping identification by vehicle scanning method [J]. Engineering Structures， 2019， 183： 637-645.

[21] TICONA MELO L R， RIBEIRO D， CALADA R， et al. Validation of a vertical train-track-bridge dynamic interaction model based on limited experimental data [J]. Structure and Infrastructure Engineering， 2020， 16（1）： 181-201.

[22] 谢青， 韩万水， 刘修平， 等. 基于模型修正的实体车桥耦合分析系统建立及验证[J]. 中国公路学报， 2018， 31（7）： 126-136.

XIE Q， HAN W S， LIU X P， et al. Development and validation of solid vehicle-bridge interaction analysis system based on model updating [J]. China Journal of Highway and Transport， 2018， 31（7）： 126-136.（in Chinese）

[23] YUAN Y G， HAN W S， LI G L， et al. Time-dependent reliability assessment of existing concrete bridges including non-stationary vehicle load and resistance processes [J]. Engineering Structures， 2019， 197： 109426.

[24] JIANG L Z， LIU X， XIANG P， et al. Train-bridge system dynamics analysis with uncertain parameters based on new point estimate method [J]. Engineering Structures， 2019， 199： 109454.

[25] HAN X， XIANG H Y， LI Y L， et al. Predictions of vertical train-bridge response using artificial neural network-based surrogate model [J]. Advances in Structural Engineering， 2019， 22（12）： 2712-2723.

[26] 向活躍， 唐平， 王涛， 等. 基于子集分裂模拟的车桥系统极值响应统计[J]. 振动与冲击， 2020， 39（5）： 105-111， 136.

XIANG H Y， TANG P， WANG T， et al. Extreme value response statistics of a vehicle-bridge system based on SS/S method [J]. Journal of Vibration and Shock， 2020， 39（5）： 105-111， 136. （in Chinese）

[27] MAO J F， YU Z W， JIANG L Z. Stochastic analysis of vehicle-bridge coupled interaction and uncertainty bounds of random responses in heavy haul railways [J]. International Journal of Structural Stability and Dynamics， 2019， 19（12）： 1950144.

[28] XIN L F， LI X Z， ZHANG J X， et al. Resonance analysis of train-track-bridge interaction systems with correlated uncertainties [J]. International Journal of Structural Stability and Dynamics， 2020， 20（1）： 2050008.

[29] XIAO X， YAN Y， CHEN B. Stochastic dynamic analysis for vehicle-track-bridge system based on probability density evolution method [J]. Engineering Structures， 2019， 188： 745-761.

[30] WAN H P， NI Y Q. An efficient approach for dynamic global sensitivity analysis of stochastic train-track-bridge system [J]. Mechanical Systems and Signal Processing， 2019， 117： 843-861.

[31] XIN L F， LI X Z， ZHU Y， et al. Uncertainty and sensitivity analysis for train-ballasted track-bridge system [J]. Vehicle System Dynamics， 2020， 58（3）： 453-471.

[32] 李小珍， 辛莉峰， 肖林， 等. 考虑轨道不平顺全概率分布的车桥随机分析方法[J]. 土木工程学报， 2019， 52（11）： 71-78.

LI X Z， XIN L F， XIAO L， et al. A stochastic analysis method of train-bridge interactions considering full probability distribution [J]. China Civil Engineering Journal， 2019， 52（11）： 71-78. （in Chinese）

[33] JIN S， FENG H D. Reliability assessment of a curved heavy-haul railway track-bridge system [J]. Structure and Infrastructure Engineering， 2020， 16（3）： 465-480.

[34] 廖海黎， 李明水， 周强. 海洋桥梁工程抗风安全的难题及其对策思考[J]. 中国工程科学， 2019， 21（3）： 12-17.

LIAO H L， LI M S， ZHOU Q. Wind resistance safety of marine bridge engineering and corresponding guarantee countermeasures [J]. Engineering Science， 2019， 21（3）： 12-17.（in Chinese）

[35] LI Y L， YU C J， CHEN X Y， et al. An efficient Cholesky decomposition and applications for the simulation of large-scale random wind velocity fields [J]. Advances in Structural Engineering， 2019， 22（6）： 1255-1265.

[36] WANG H， XU Z D， FENG D M， et al. Non-stationary turbulent wind field simulation of bridge deck using non-negative matrix factorization [J]. Journal of Wind Engineering and Industrial Aerodynamics， 2019， 188： 235-246.

[37] 靖洪淼， 廖海黎， 周強， 等. 一种山区峡谷桥址区风场特性数值模拟方法[J]. 振动与冲击， 2019， 38（16）： 200-207.

JING H M， LIAO H L， ZHOU Q， et al. A numerical simulation method for wind field characteristics of mountainous valley at bridge site [J]. Journal of Vibration and Shock， 2019， 38（16）： 200-207.（in Chinese）

[38] 徐曼， 郭薇薇， 夏禾， 等. 大跨度公铁两用斜拉桥三维风速场实测与模拟[J]. 哈尔滨工业大学学报， 2019， 51（3）： 107-113.

XU M， GUO W W， XIA H， et al. 3D wind field measurement and simulation of a long-span cable-stayed rail-cum-road bridge [J]. Journal of Harbin Institute of Technology， 2019， 51（3）： 107-113.（in Chinese）

[39] 何佳骏， 向活跃， 龙俊廷， 等. 大风攻角下桥隧过渡段CRH3型列车气动特性和安全性分析[J/OL]. 西南交通大学学报， http：//kns.cnki.net/kcms/detail/51.1277.U.20200320.1138.004.html.

HE J J， XIANG H Y， LONG J T， et al. Aerodynamic characteristics and safety analysis when CRH3 passing through bridge-tunnel transition at large wind attack angle [J/OL]. Journal of Southwest Jiaotong University， http：//kns.cnki.net/kcms/detail/51.1277.U.20200320.1138.004.html. （in Chinese）

[40] 李小珍， 唐庆， 吴金峰， 等. 桥塔遮风效应对移动列车气动参数及行车安全的影响[J]. 中国公路学报， 2019， 32（10）： 191-199.

LI X Z， TANG Q， WU J F， et al. Influence of the bridge tower shielding effect on aerodynamic parameters and running safety of moving train [J]. China Journal of Highway and Transport， 2019， 32（10）： 191-199.（in Chinese）

[41] 刘昊苏， 雷俊卿. 大跨度双层桁架主梁三分力系数识别[J]. 浙江大学学报（工学版）， 2019（6）： 1092-1100.

LIU H S， LEI J Q. Identification of three-component coefficients of double deck truss girder for long-span bridge [J]. Journal of Zhejiang University （Engineering Science）， 2019（6）： 1092-1100.（in Chinese）

[42] MA C M， WANG J X， LI Q S， et al. 3D aerodynamic admittances of streamlined box bridge decks [J]. Engineering Structures， 2019， 179： 321-331.

[43] LI M， LI M S， SU Y. Experimental determination of the two-dimensional aerodynamic admittance of typical bridge decks [J]. Journal of Wind Engineering and Industrial Aerodynamics， 2019， 193： 103975.

[44] XIANG H Y， LI Y L， CHEN S R， et al. Wind loads of moving vehicle on bridge with solid wind barrier [J]. Engineering Structures， 2018， 156： 188-196.

[45] REN W M， DUAN Q S， MA C M， et al. Experimental investigation of the protective effect of wind barriers on high-speed railway bridge in inland strong wind area： [J]. Advances in Structural Engineering， 2019， 22（15）： 3306-3318.

[46] HE X H， FANG D X， LI H， et al. Parameter optimization for improved aerodynamic performance of louver-type wind barrier for train-bridge system [J]. Journal of Central South University， 2019， 26（1）： 229-240.

[47] 韩艳， 刘叶， 胡朋. 非定常气动荷载对桥上列车行驶安全舒适性影响分析[J]. 铁道科学与工程学报， 2020， 17（1）： 118-128.

HAN Y， LIU Y， HU P. Impact analysis of unsteady aerodynamic loads on the safety and comfort of trains running on bridges [J]. Journal of Railway Science and Engineering， 2020， 17（1）： 118-128. （in Chinese）

[48] HE X H， SHI K， WU T. An efficient analysis framework for high-speed train-bridge coupled vibration under non-stationary winds [J]. Structure and Infrastructure Engineering， 2020， 16（9）： 1326-1346.

[49] GUO X R， TANG J F. Effects of wind barrier porosity on the coupled vibration of a train-bridge system in a crosswind [J]. Structural Engineering International， 2019， 29（2）： 268-275.

[50] 李小珍， 秦羽， 劉德军. 侧风作用下五峰山长江大桥列车行车安全控制[J]. 铁道工程学报， 2018， 35（7）： 58-64.

LI X Z， QIN Y， LIU D J. The safety control of train running on the Wufeng mountain Yangtze River bridge under crosswind [J]. Journal of Railway Engineering Society， 2018， 35（7）： 58-64.（in Chinese）

[51] 刘高， 陈上有， 王昆鹏， 等. 跨海公铁两用桥梁车桥-风浪流耦合振动研究[J]. 土木工程学报， 2019， 52（4）： 72-87.

LIU G， CHEN S Y， WANG K P， et al. Study on coupling vibration of vehicle-bridge-wind-wave-current system of rail-cum-road sea bridge [J]. China Civil Engineering Journal， 2019， 52（4）： 72-87. （in Chinese）

[52] 李永乐， 房忱， 向活跃. 风-浪联合作用下大跨度桥梁车桥耦合振动分析[J]. 中国公路学报， 2018， 31（7）： 119-125.

LI Y L， FANG C， XIANG H Y. Coupled vibration analysis of vehicle-bridge for long-span bridge under wind and wave [J]. China Journal of Highway and Transport， 2018， 31（7）： 119-125.（in Chinese）

[53] 魏凯， 沈忠辉， 吴联活， 等. 强台风作用下近岸海域波浪风暴潮耦合数值模拟[J]. 工程力学， 2019， 36（11）： 139-146.

WEI K， SHEN Z H， WU L H， et al. Coupled numerical simulation on wave and storm surge in coastal areas under strong typhoons [J]. Engineering Mechanics， 2019， 36（11）： 139-146.（in Chinese）

[54] 魏凯， 林静， 李明阳. 基于外海环境预报的近岸岛礁桥址区波高ANN推算模型[J]. 土木与环境工程学报（中英文）， 2019， 41（6）： 89-94.

WEI K， LIN J， LI M Y. ANN model of wave height in nearshore island area for sea-crossing bridge based on open ocean environmental forecasting [J]. Journal of Civil and Environmental Engineering， 2019， 41（6）： 89-94.（in Chinese）

[55] CHEN L K， QIN H X， JIANG L Z， et al. A near-fault vertical scenario earthquakes-based generic simulation framework for elastoplastic seismic analysis of light rail vehicle-viaduct system [J]. Vehicle System Dynamics， 2020： 1-25.

[56] 沈毓婷. 近断层脉冲地震动对无砟轨道结构及行车安全性影响研究[D]. 成都： 西南交通大学， 2019.

SHEN Y T. Study on the influence of near-fault pulse ground motion on ballastless track structure and driving safety [D]. Chengdu： Southwest Jiaotong University， 2019. （in Chinese）

[57] 乔宏， 夏禾， 杜宪亭. 地震动斜入射对车桥系统地震响应的影响[J]. 哈尔滨工程大学学报， 2019， 40（9）： 1629-1635.

QIAO H， XIA H， DU X T. Effect of oblique incidence of seismic wave on seismic response of a train-bridge system [J]. Journal of Harbin Engineering University， 2019， 40（9）： 1629-1635. （in Chinese）

[58] 雷虎军. 非一致地震激励下列车轨道桥梁耦合振动及行车安全性研究[D]. 成都： 西南交通大学， 2014.

LEI H J. Coupling vibration and running safety of train-track-bridge system under non-uniform seismic excitations [D]. Chengdu： Southwest Jiaotong University， 2014. （in Chinese）

[59] 國巍， 李君龙， 刘汉云. 强地震下高速铁路桥上行车精细化模拟及行车安全性分析[J]. 工程力学， 2018， 35（Sup1）： 259-264， 277.

GWO W， LI J L， LIU H. The analysis of running safety of high-speed-train on bridge by using refined simulation considering strong earthquake [J]. Engineering Mechanics， 2018， 35（Sup1）： 259-264， 277.（in Chinese）

[60] ZENG Q， DIMITRAKOPOULOS E G. Vehicle-bridge interaction analysis modeling derailment during earthquakes [J]. Nonlinear Dynamics， 2018， 93（4）： 2315-2337.

[61] BORJIGIN S， KIM C W， CHANG K C， et al. Nonlinear dynamic response analysis of vehicle-bridge interactive system under strong earthquakes [J]. Engineering Structures， 2018， 176： 500-521.

[62] 胡川川. 地震作用下铁道车辆桥上脱轨概率研究[D]. 成都： 西南交通大学， 2019.

HU C C. Study on derailment probability of railway vehicles on bridges shaken by earthquake [D]. Chengdu： Southwest Jiaotong University， 2019. （in Chinese）

[63] JIN Z B， PEI S L， LI X Z， et al. Effect of vertical ground motion on earthquake-induced derailment of railway vehicles over simply-supported bridges [J]. Journal of Sound and Vibration， 2016， 383： 277-294.

[64] WEI B， YANG T H， JIANG L Z， et al. Effects of uncertain characteristic periods of ground motions on seismic vulnerabilities of a continuous track-bridge system of high-speed railway [J]. Bulletin of Earthquake Engineering， 2018， 16（9）： 3739-3769.

[65] 雷虎军， 黄江泽. 地震作用下445 m上承式高速铁路拱桥行车安全分析[J]. 铁道标准设计， 2018， 62（11）： 88-93.

LEI H J， HUANG J Z. Train running safety analysis of high-speed railway deck arch bridge of 445 m span under earthquake action [J]. Railway Standard Design， 2018， 62（11）： 88-93. （in Chinese）

[66] 李昊， 張鸿儒， 于仲洋. 高速铁路地震预警阈值随机振动分析[J]. 振动工程学报， 2019， 32（5）： 874-885.

LI H， ZHANG H R， YU Z Y. Dynamic response analysis of wheel-track and train early warning threshold under earthquake [J]. Journal of Vibration Engineering， 2019， 32（5）： 874-885. （in Chinese）

[67] 李昊， 张鸿儒， 于仲洋， 等. 地震作用下车辆轨道系统轮轨动态响应试验研究[J]. 振动与冲击， 2020， 39（2）： 132-140.

LI H， ZHANG H R， YU Z Y. Stochastic vibration analysis of earthquake early warning threshold for high speed railway [J]. Journal of Vibration and Shock， 2020， 39（2）： 132-140. （in Chinese）

[68] ZHANG M， LUO S H， GAO C， et al. Research on the mechanism of a newly developed levitation frame with mid-set air spring [J]. Vehicle System Dynamics， 2018， 56（12）： 1797-1816.

[69] SUN Y G， XU J Q， QIANG H Y， et al. Hopf bifurcation analysis of maglev vehicle-guideway interaction vibration system and stability control based on fuzzy adaptive theory [J]. Computers in Industry， 2019， 108： 197-209.

[70] SUN Y G， XU J Q， QIANG H Y， et al. Adaptive sliding mode control of maglev system based on RBF neural network minimum parameter learning method [J]. Measurement， 2019， 141： 217-226.

[71] LI Q， WANG H， SHEN G. Research on control method of Maglev vehicle-guideway coupling vibration system based on particle swarm optimization algorithm [J]. Journal of Vibration and Control， 2019， 25（16）： 2237-2245.

[72] ZHANG L， HUANG J Y. Dynamic interaction analysis of the high-speed maglev vehicle/guideway system based on a field measurement and model updating method [J]. Engineering Structures， 2019， 180： 1-17.

[73] HUANG S， LI Z W， YANG M Z. Aerodynamics of high-speed maglev trains passing each other in open air [J]. Journal of Wind Engineering and Industrial Aerodynamics， 2019， 188： 151-160.

[74] LI X Z， WANG D X， LIU D J， et al. Dynamic analysis of the interactions between a low-to-medium-speed maglev train and a bridge： Field test results of two typical bridges [J]. Proceedings of the Institution of Mechanical Engineers， Part F： Journal of Rail and Rapid Transit， 2018， 232（7）： 2039-2059.

[75] WANG D X， LI X Z， LIANG L， et al. Influence of the track structure on the vertical dynamic interaction analysis of the low-to-medium-speed maglev train-bridge system [J]. Advances in Structural Engineering， 2019， 22（14）： 2937-2950.

[76] WANG D X， LI X Z， WANG Y W， et al. Dynamic interaction of the low-to-medium speed maglev train and bridges with different deflection ratios： Experimental and numerical analyses [J]. Advances in Structural Engineering， 2020， 23（11）： 2399-2413.

[77] 王黨雄， 李小珍， 耿杰， 等. 低速磁浮列车在简支梁上运行和静悬浮时的耦合振动试验研究[J]. 土木工程学报， 2018， 51（9）： 75-83.

WANG D X， LI X Z， GENG J， et al. Experimental study on coupling vibrations of low-speed maglev trains moving and standing still on simply-supported girders [J]. China Civil Engineering Journal， 2018， 51（9）： 75-83.（in Chinese）

[78] 李小珍， 王党雄， 耿杰， 等. F轨对中低速磁浮列车桥梁系统竖向耦合振动的影响研究[J]. 土木工程学报， 2017， 50（4）： 97-106.

LI X Z， WANG D X， GENG J， et al. Study on the influence of F-rail in vertical coupling vibration of low-medium speed maglev train-bridge system [J]. China Civil Engineering Journal， 2017， 50（4）： 97-106.（in Chinese）

（编辑 胡玲）