高职院校高等数学融入课程思政的教学策略——以“数列的极限”为例

杨 静

（唐山职业技术学院，河北 唐山 063000）

1 教学设计

1.1 提出问题

我国古代数学是世界数学发展不可忽视的一直源头，公元263年，数学家刘徽在《九章算术》里提出的割圆术将圆周率精确到小数后两位，而割圆术“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体，而无所失矣。”这种对极限思想的描述比欧洲早了一千多年。

在很长一段时间内，人们试图采用各种方法去近似计算圆的面积，而我国的刘徽在注解《九章算术》时提出的割圆术，是一种很好的方法。他用圆的内接或外切正多边形穷竭的方法求出圆面积和周长，割圆术的做法如图所示：

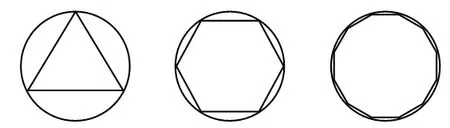
图1

先作圆的内接正三角形，面积记为A1，再作圆的内接正六边形，其面积记为A2，再作圆的内接正十二边形，其面积记为A3，…，照这样下去，把圆的内接正3×2n-1边形的面积记为An，这样得到一组数列，从图形的直观上不难看出：随着圆内接正多边形边数的增加，圆内接正多变形的面积与圆面积越来越接近。

通过对数学史的介绍引出了数列极限的定义，让学生了解到我国数学史上的一些辉煌的成就，虽然由于当时时代的限制和研究方向等因素的影响，刘徽没能将其总结形成理论，但是刘徽提出的“割圆术”“阳马术”这种极限思想比欧洲早了一千多年，使学生在了解数学史的同时增强民族认同感和自信心，通过介绍数学史及数学家的故事，鼓励学生要善于发现问题、提出问题、分析问题、解决问题，在遇到困难的时候要克服心理上的畏难情绪，踏实学习，勇于挑战。

1.2 概念的建立

体会刘徽的割圆术思想，通过观察图像的动态变化，抽象得出数列极限的概念：对于数列 {un}，如果当n无限增大时，通项nu无限接近于某个确定的常数A，则称A为数列{un}的极限，或称数列{un}收敛于A，记为或un→A,n→∞．若数列{un}没有极限，则称该数列发散．

1.3 知识巩固

理解概念解决下列数列的极限问题

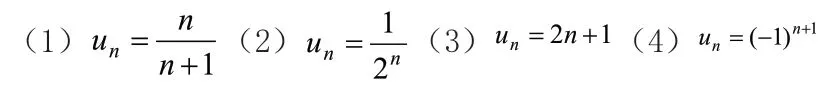
通过解决这些数列的极限问题，巩固数列极限的概念，让学生体会这种变化的过程，让学生进一步理解极限思想。

1.4 知识拓展

带领学生研究Koch分形曲线，Koch分形从一条直线段开始，首先画一个线段，把它平均分成三段，将线段中间的三分之一部分用一个等边三角形的另两条边代替，形成一个新的图形；在新的图形中，按照如上方法，再次形成新的图。如此迭代，每一次等分并向外作正三角形称为一次递归。引导学生完成n次递归所得的周长an，并求n无限增大时an的极限

接着提出问题，用无限长的周长一定能围住一块无限大的面积吗？带领学生进一步探索“雪花曲线”。用一个边长为1的等边三角形的每条边作如上的递归过程，经过无限次递归曲线的形状接近理想化的雪花，这个神奇的雪花被人们称为Koch雪花。观察雪花曲线的形成过程很快就会发现，雪花曲线的周长是无限长的，但是面积却是有限的。这和我们了解的周长越长面积越大的结论相反，通过这个问题告诉同学们遇到问题要理性的思考，科学的证明。

1.5 课后思考

存款分析：某人有本金A元，若银行存款的年利率为r，不考虑个人所得税的情况下，建立此人n年末的本利和数列，并分析此数列的极限，解释其实际意义。

通过课后思考题，让学生进一步掌握数列极限的计算，体会数学来源于生活中又服务于我们的生产生活。

2 教学效果与评价

1）通过对割圆术的探索，引导学生总结数列极限的概念，介绍中国数学家的数学成就，让学生感受民族自豪感，增强文化自信心，对比近代数学的落后激起学生强烈的民族责任感，通过正面的引导，使学生不仅学习了数学专业知识也激发了爱国主义情怀。

2）在概念的形成及巩固阶段，通过动画演示，数形结合，静动结合，让学生在变化中找规律，探索事物的本质。

3）在知识拓展部分选取了“Koch曲线”这个神奇而又美丽的曲线，引导学生理想思考，科学论证，在介绍完“Koch曲线”形成原理后，可以进一步引导计算机专业的学生利用“C++”等已经学习的计算机语言画出Koch曲线。在引导学生做题的同时，体会数学的内涵 之美。

3 结语

高等数学是高职院校最重要的基础课之一，课程思政融入教学，而非将数学课程讲成思政课，数学课程教师应不断提升自身政治修养，坚定政治意识，秉承“教书育人”的理念，始终把高等教学与学生的人格完善教育结合起来，开拓思路，不断创新，把思政元素与专业知识很好的融合，在潜移默化中实现润物无声，努力成为学生品格、品行的教育者和引领者。