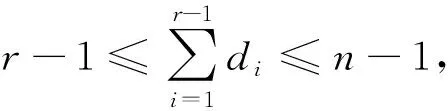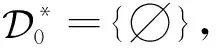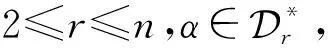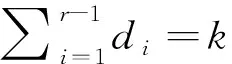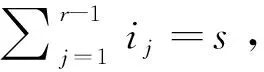半群OEXn的组合结果

王 芳，杨秀良

(杭州师范大学理学院，浙江 杭州 311121)

0 引言和主要结果叙述

设IOn={α∈In|∀x,y∈dom(α),x≤y⟹xα≤yα}是有限集Xn={1,2,…,n}上的部分一一保序变换半群,它引起了人们极大的关注[1-5].最近,Al-Kharousi等[6]研究了IOn的保序等距子半群

ODPn={α∈IOn|∀x,y∈dom(α),|x-y|=|xα-yα|}∪{∅}.

文献[7]将ODPn推广到IOn的更大的子半群,即保序扩张半群

OEXn={α∈IOn|∀x,y∈dom(α),|x-y|≤|xα-yα|}∪{∅}，

本文的主要结果如下:

定理1半群OEXn的阶为

1 主要结果的证明

为叙述方便, 先作如下准备.

对α∈OEXn,dom(α)和im(α)依次表示α的定义域和值域,令|im(α)|=r,且

其中a1

g(dom(α))=(|a2-a1|,|a3-a2|,…,|ar-ar-1|)，

g(im(α))=(|a2α-a1α|,|a3α-a2α|,…,|arα-ar-1α|).

给定g(dom(α))所对应的定义域集和值域集如下:

dom(g(dom(α)))={{p,p+d1,p+d1+d2,…,p+k}|1≤p≤n-k}，

im(g(dom(α)))={{p,p+d1+i1,p+d1+d2+i1+i2,…,p+k+s}|0≤s≤n-k-1,1≤p≤n-k-s}.

例如,α∈OEX4,且|im(α)|=3,设g(dom(α))=(1,1),则g(dom(α))所对应的定义域集和值域集分别为:

dom(g(dom(α)))={{1,2,3},{2,3,4}}，

im(g(dom(α)))={{1,2,3},{2,3,4},{1,3,4},{1,2,4}}.

引理1对n≥1,则F(n,0)=1，F(n,1)=n2.

□

x1+x2+…+xr-1=k-r+1

的非负整数解的个数.由[11,推论3.5.3],可得所求的个数为

因此当3≤r≤n时,结论成立.

综上可得结论成立.

集合X表示从数集{1,2,…,n-k+r-1}中任意取出r个数组成的集合{x1,x2,…,xr}的全体,其中x1

X={{p,p+i1+1,p+i1+i2+2,…,p+s+r-1}|0≤s≤n-k-1,1≤p≤n-k-s},

Y={{p,p+d1+i1,p+d1+d2+i1+i2,…,p+k+s}|0≤s≤n-k-1,1≤p≤n-k-s}.

证明给定集合

X={{p,p+i1+1,p+i1+i2+2,…,p+s+r-1}|0≤s≤n-k-1,1≤p≤n-k-s}.

Y={{p,p+d1+i1,p+d1+d2+i1+i2,…,p+k+s}|0≤s≤n-k-1,1≤p≤n-k-s}.

因此我们只需找一个从X映到Y的双射即可.现有映射f:X→Y为

只需证映射f是一个双射.

任取a,b∈X且a≠b,令a=(a1,a2,…,ar),b=(b1,b2,…,br), 从而

f(a)=f(a1,a2,…,ar)=(a1,a2+d1-1,a3+d1+d2-2,…,ar+k-r+1)=(l1,…,lr),

f(b)=f(b1,b2,…,br)=(b1,b2+d1-1,b3+d1+d2-2,…,br+k-r+1)=(m1,…,mr).

由于a≠b, 必存在t使at≠bt,因

lt=at+(d1+d2+…+dt-1)-t+1,

mt=bt+(d1+d2+…+dt-1)-t+1,

故lt≠mt.因此f(a)≠f(b),即f是一个单射.

现任取{y1,y2,…,yr}∈Y,必存在

c={y1,y2-d1+1,y3-d1-d2+2,…,yr-k+r-1},

由1≤y1

1≤y1

种情况.因r-1≤k≤n-1,故

令k=r+i-2,得

|OEXn|=F(n,0)+F(n,1)+F(n,2)+F(n,3)+…+F(n,n).

由引理1和引理4得

以下给出第二个主要结果的证明.

ij≥dj,k≤s≤n-1(j∈{1,2,…,r-1}).

i1+i2+…+ir-1=s

满足条件i1≥d1,i2≥d2,…,ir-1≥dr-1的整数解的个数.设x1=i1-d1,x2=i2-d2,…,xr-1=ir-1-dr-1,则等价于

x1+x2+…+xr-1=s-k

的非负整数解的个数.由[11,推论3.5.3],可得所求的个数为

因k≤s≤n-1,故(i1,i2,…,ir-1)共有

种情况.

当r=2时,则g(dom(α))=(d1),g(im(α))=(i1),由|x1-x2|≤|a1-a2|, 从而

1≤d1≤i1≤n-1,

综上可得结论成立.

结论成立.

结论成立.

结论成立.