Effect of rotation on the surface wave propagation in magneto-thermoelastic materials with voids
2020-12-12FarhanAbdAlla
A.M.Farhan ,A.M.Abd-Alla
a Physics Department, Faculty of Science, Jazan University, Saudi Arabia
b Physics Department, Faculty of Science, Zagzig University, Egypt
c Mathematics Department, Faculty of Science, Sohag University, Egypt
Abstract
Keywords: Green Lindsay theory;Thermoelasticity;Surface waves.
1.Introduction
Theory of linear elastic materials with voids is an important generalization of the classical theory of elasticity.The theory is used for investigating various types of geological and biological materials for which classical theory of elasticity is not adequate.The theory of linear elastic materials with voids deals the materials with a distribution of small pores or voids,where the volume of void is included among the kinematics variables.The theory reduces to the classical theory in the limiting case of the volume of void tending to zero.Such problems have attracted much attention and have undergone a certain development (in Refs.[1-4]).Surface waves have been well recognized in the study of earthquake,seismology,geophysics and Geodynamics.These waves usually have greater amplitudes as compared with body waves and travel more slowly than body waves.There are many types of surface waves but we only discussed Stoneley and Rayleigh waves.In earthquake the movement is due to the surface waves.These are also used for detecting cracks and other defects in materials.Lord Rayleigh [3] was the first to observe such kind of waves in 1885.That’s why we called it Rayleigh waves.Sengupta and Nath [5] investigated surface waves in fibre-reinforced anisotropic elastic media,but their decomposition of displacement vector was not correct due to which some errors are found in their investigations[6].The idea of continuous self-reinforcement at every point of an elastic solid was introduced by Belfield et al.[7].The superiority of fibre-reinforced composite materials over other structural materials attracted many authors to study different types of problems in this field.Fibre-reinforced composite structures are used due to their low weight and high strength.Two important components,namely concrete and steel of a reinforced medium are bound together as a single unit so that there can be no relative displacement between them i.e.they act together as a single anisotropic unit.The artificial structures on the surface of the earth are excited during an earthquake,which give rise to violent vibrations in some cases.Engineers and architects are in search of such reinforced elastic materials for the structures that resist the oscillatory vibration.The propagation of waves depends upon the ground vibration and the physical properties of the material structure.Surface wave propagation in fiber reinforced media was discussed by various authors.In the classical theory of elasticity,the voids is an important generalization.Nunziato and Cowin [8] and Cowin and Nunziato [9] discuss the theory in elastic media with voids.Puri and Cowin [10] studied the effects of voids on plane waves in linear elastic media and it is evident that pure shear waves remain unaffected by the presence of pores.Theory of thermoelastic material with voids is investigated by Lesan [11].Good amount of literature on surface wave propagation in a generalized thermoelastic material with voids,is available in Singh and Pal [12] and references therein.Chandrasekharaiah [13] and [14] discussed the effects of voids on propagation of plane and surface waves.Abo-Dahab [15] investigated the propagation of P waves from stress-free surface elastic half-space with voids.The effect of gravity on wave propagation in an elastic solid medium was first considered by Bromwich [16].Later on gravity effects on wave propagation were discussed by various authors[17-20].Surface waves in fiber-reinforced,general viscoelastic media of higher order under gravity is discussed by kakar et al.[21] whereas Pal and Sengupta [22] studied the gravitational effects in viscoelastic media.Ren et al.[23] investigated the coupling effects of void shape and void size on the growth of an elliptic void in a fiber-reinforced hyper-elastic thin plate.Vishwakarma et al.[24] discussed the influence of rigid boundary on the love wave propagation in elastic layer with void pores.Tvergaard [25] studied the elasticplastic void expansion in near-self-similar shapes.Fonseca et al.[26] expressed the material voids in elastic solids with anisotropic surface energies.The extensive literature on the topic is now available and we can only mention a few recent interesting investigations in refs [27-38].
The present discussion aims at investigating the propagation of surface waves in a generalized magneto-thermoplastic materials taking GL model with voids and rotation.The general surface wave speed is derived to study the effect of magnetic field,rotation and voids on surface waves.The results obtained in this investigation are more general in the sense that some earlier published results are obtained from our result as special cases.Moreover,influence of magnetic field(due to rotation) on the thermoelastic response is being studied in a homogeneous thermally conducting elastic medium having a void in the half-space in the medium.
2.Formulation of the problem
We consider a homogeneous isotropic elastic half spacez≥0.We choose rectangular coordinate system (x,y,z)whereaszis pointing towards the medium.The medium is assumed to be rotating with uniform angular velocity=(0,Ω,0)with respect to the magnetic field→H=(0,H0,0)is applied in theydirection as a result,there would be an induced electric field→Eand an induced magnetic field→h.
Folloing Wang and Dong [38],the governing electrodynamic Maxwell equations are:

whereis the perturbed magnetic field over the primary magnetic field,is the electric intensity,is the electric current density,µeis the magnetic permeability,is the constant primary magnetic field andis the displacement vector.Considering an isotropic elastic solid under a magnetic fieldacting on y-axis.The elastic medium is rotating uniformly with an angular velocityΩ=Ωnwherenis a unit vector representing the direction of the axis of rotation.The displacement equation of motion in the rotating frame has two additional term centripetal acceleration,×(×)due to time varying motion only.
The stress-strain-temperature relations,due to linearly thermoelastic medium,are (see Refs.[11,12]) given by

The Maxwell ’ s electro-magnetic stress tensorτijis given by
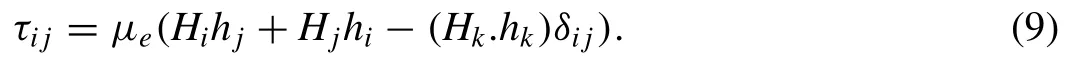
The basic governing dynamical equations for a homogeneous,isotropic thermoelastic solid after including the Coriolis and Centrifugal forces,in the absence of body forces and body couples are given [2]:

which it tends to
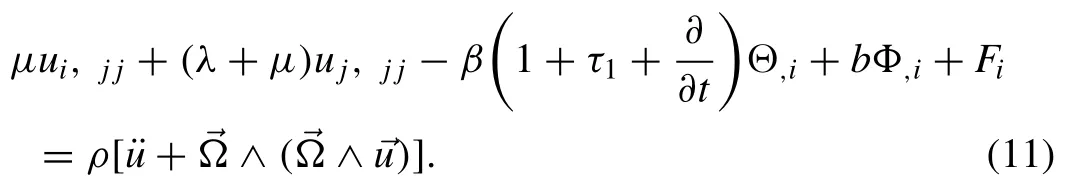
The heat conduction equation ([12]) is given by:

The voids equation is

whereα,b,m,ξare the void material parameters,αtis the coefficient of linear thermal expansion,ηis the entropy per unit mass,Θis the temperature,λandµare Lame’s constants,µeis the magnetic permeability,ρis the density,qiare the components of the heat flux vector,τ0andτ1are the thermal relaxations parameters,Φis the change in the volume fraction field,χis the equilibrated inertia,Ceis the specific heat per unit mass,g is the intrinsic equibrated body forces,K is the thermal conductivity,T0is the natural temperature of thmedum,Tis the absolute temperature,Siare the components of the equilibrated stress vector andis Lorentz’s force.
The Eqs.(11)-(13) are written in x-z plane as

where

Now vector and scalar potentialsψandφare defined

Using Eq.(18) in Eqs.(14)-(17),we get

where

3.Solution of the problem
In order to examine the possibility of a plane wave propagation in the medium under consideration,we shall assume a solution of governing Eqs.(19-21) in the form

Substituting from Eq.(23),into Eqs.(19)-(21),we obtain the following set of equations

The elimination ofφ1,Θ1andΦ1from Eqs.(24)-(26),we get
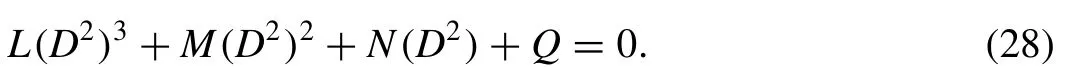
where

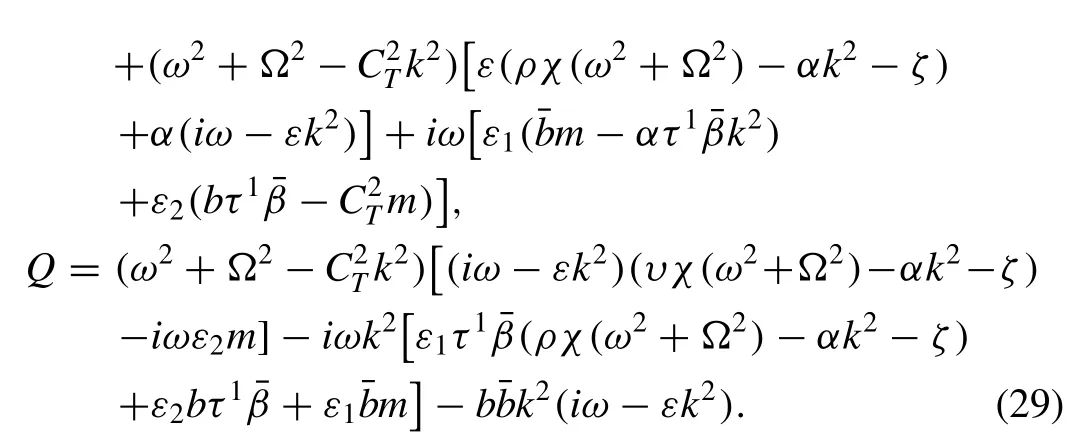
Thus the solution of Eq.(28) which are bound asz→ ∞have the following form

wherem1,m2,m3are the positive roots of the Eq.(28),

The general solutionsψof the Eq.(19a) are written as

where

4.Boundary conditions
If the thermoelastic interactions are caused by a uniform step in temperature applied to the boundary of the half-space which is held in stress-free state,then the following boundary conditions hold:

Substitution from Eqs.(2),(9),(30-32),(34) and (35-38)into the boundary condition Eq.(39),we get

where

If the magnetic field is neglected,the results obtained are deduced to the relevant results obtained by Abo-Dahab and Abd-Alla [3].
5.Numerical results and discussion
The present study focuses on the effects of rotation,magnetic field and void pores of the medium on the propagation of plane waves in a solid.For numerical discussion,we have considered three sets of values of relevant parameters from the works of [31] as given below;

Fig.1.Variations of the non-dimensional frequency with respect to magnetic field at τ0=0.05 and Ω=1.3,for the three modes.

Fig.2.Variations of the non-dimensional frequency with respect to magnetic field at τ0=0.05 and Ω=1.3,for the three modes.


For numerical computational purposes Matlab simulation technique is adopted.The variations of non-dimensional frequency of the magneto-thermoelastic material is shown graphically in Figs.1-7 for a thermo-elastic medium with voids in presence of a uniform rotation.

Fig.3.Variations of the non-dimensional frequency with respect to magnetic field at τ0=0.05 and Ω=1.3,for the three modes.

Fig.4.Variations of the non-dimensional frequency with respect to magnetic field at τ0=0.05 for different values of rotation Ω.
Using these values,it was found thatω=0.01,T0=298K.
Fig.1 illustrates the effect of magnetic field on the nondimensional frequency,which it increases with increasing of magnetic field in the whole range of theH0-axis for three modes.The non-dimensional frequency smaller except those of the lower modes vibrations with increase and become larger with an increase of the magnetic field of the two mediums.
In Fig.2,the effect of magnetic field on the nondimensional frequency in the whole range of theH0-axis for three modes as shown in Fig.(1).It’s obvious that the nondimensional frequency increases with increasing of magnetic field.For a specified magnetic field,the non-dimensional frequency of the medium with the parabolically varying magnetic field are the largest.This order corresponds to that of the medium,as shown in Fig.(3).is drawn to exhibit the reason for this ordering is that the increase of the magnetic field is more effective than that of the mass on the natural frequencies of the medium.

Fig.5.Variations of the non-dimensional frequency with respect to magnetic field at Ω=1.3 for different values the thermal relaxations τ0.

Fig.6.Variations of the non-dimensional frequency with respect to rotation Ω at τ0=0.05 for different values the magnetic field.
In Fig.4,a graphical representation is given for variations the non-dimensional frequency with respect to the magnetic field for the medium,which it has increased with the rotationΩand magnetic field.We can also observe from Fig.(4) that the non-dimensional frequency stays basicallyH0invariable when the rotationΩis a large.An obvious trend in that non-dimensional frequency for higher mode number 3 is always larger than the corresponding one for lower 3,is also obtained.
From the Fig.5,it has been observed that the variation of the shows the variations of the non-dimensional frequency with respect to the magnetic fieldH0of the rotating medium,which it has decreased with increasing of the relaxation time and magnetic field.The figure shows the deflection of the vibration modes without nodal circles,where the maximum deflection rising at the free edge is taken as unity.
From the Fig.6,it is observed that the variations of the non-dimensional frequency with respect to the rotationΩfor the rotating medium,which it has increased with the increasing of the magnetic field and rotation.Since for larger rotation the non-dimensional frequency stay nearly invariable,as indicated above,only two typical values of rotation are considered.
Fig.7 delineates the effect of relaxation time associated with rotation elastic half space with the non-dimensional frequency for the medium,which it has oscillatory behavior in the whole range of theΩ-axis,which it decreases with increasing of relaxation timeτ0.
The present method of using a half-interval method is very simple and clear as an analytical process,and therefore has significant computational advantages.This method is recommended for application to vibration problems of continuous systems such as half-space and plates.

Fig.7.Variations of the non-dimensional frequency with respect to rotation Ω at τ0=0.05 for different values the relaxation times.
6.Conclusion
This article directly used Lame’s potential method to study the surface wave propagation in magneto-thermoelastic problems of homogeneous,isotropic material with half-space based on two dimensional thermoelasticity.Due to rotation,the Coriolis and Centrifugal forces act as the cause of damping on thermoelastic voids.It is noticed that due to rotation the effect of thermo-elastic voids into the medium is much lesser at the periphery of the half-space.Here we are concentrating on the impact of magnetothermo-elastic voids into the homogeneous solids in very short time duration such that the influence of magnetic field as well as voids be taken into account.With the view of theoretical analysis and numerical computation,we can conclude the following phenomena:
1.The present article provides a detailed analysis of voids responses on surface wave propagation of magnetothermoelastic disturbance in an unbounded elastic medium in the presence of a magnetic field applied to the traction free boundary of the half-space.
2.The theoretical analysis and computational results confirm that the magnetic field and rotation can increase the disturbance in surface wave propagation of the thermoelastic field with respect to the classical coupled thermoelasticity model.
3.One can select the appropriate amount of rotation to enhance the effect of magnetic field on surface wave propagation of thermoelasticity.It is encouraging that voids will also make sense in comparison other thermoelastic.
The Results presented in this article may be useful for researchers who are working on material science,mathematical physics,and thermodynamics with low temperatures as well as the development of the hyperbolic thermoelastic theory.
杂志排行
Journal of Ocean Engineering and Science的其它文章
- Distortion performance of underwater acoustic mobile networks
- A modeling method for vibration analysis of cracked beam with arbitrary boundary condition
- Ship speed power performance under relative wind profiles in relation to sensor fault detection
- Role of mesoscale eddies on atmospheric convection during summer monsoon season over the Bay of Bengal:A case study
- The gravity impact in a rotating micropolar thermoelastic medium with microtemperatures
- Iterative algorithm for parabolic and hyperbolic PDEs with nonlocal boundary conditions
