水泥稳定碎石强度的测量不确定度分析

谢佳伟，唐利民*，肖约，蔡婉

(1.长沙理工大学 公路养护技术国家工程实验室，湖南 长沙 410114; 2.中交四航局广州南沙工程有限公司)

水泥稳定碎石材料的强度是衡量基层耐久性的重要指标。国内外大都采用多种耗资少、周期短的室内强度试验方法来研究其力学性能。为了准确测得水泥稳定碎石的强度，JTG D50-2017《公路沥青路面设计规范》对强度的测试方法和测试结果都有很高的要求。为了分析误差因素并定量评价误差大小，众多国际组织联合起来提出了测量不确定度理论。相比于传统的误差概念，不确定度理论用误差在某一置信水平下可能落入的区间来表征测量结果的质量，该评定与表示方法更符合实际情况，也更科学。

近年来，随着测量不确定度理论的逐步完善，其科学的评定方法已经得到了国内外众多学者的认可，并在材料力学试验和车辆碰撞模型等方面均有所应用，且取得了较为成功的研究成果。上述研究推广了测量不确定度的应用领域，然而，在道路工程中，很少有关于提高基层材料强度结果精确性的研究。由于缺乏考虑试验不确定性带来的影响，导致目前的研究结果往往与实际情况存在一定的偏差。

水泥稳定碎石强度试验结果的偏差大，为了有效评价强度结果，JTG D50-2017《公路沥青路面设计规范》对测量结果附加了平均值、标准差、变异系数和95%保证率值的要求，其数据处理程序较为繁琐，并且无法直观地呈现强度结果的偏差范围。因此，有必要对水泥稳定碎石的强度进行不确定度的评定与分析，并获得一种直观准确的表示方法。该文根据JTG E51-2009《公路工程无机结合料稳定材料试验规程》(以下简称“规程”)，采用MTS材料测试系统对水泥稳定碎石进行3种应力状态下的强度试验，根据GB/T 27418-2017《测量不确定度评定与表示方法》(以下简称“方法”)，分析并评定3种应力状态下的强度测量不确定度。

1 试件成型与试验准备

1.1 原材料与配合比

水泥稳定碎石选用复合硅酸盐水泥，强度等级为PC.32.5级，水泥剂量为5%，按照规程检验各项技术指标，检测结果如表1所示。集料采用石灰岩，经检测，其技术指标均满足规程要求。水泥稳定碎石的级配设计如图1所示。

表1 水泥指标检验结果

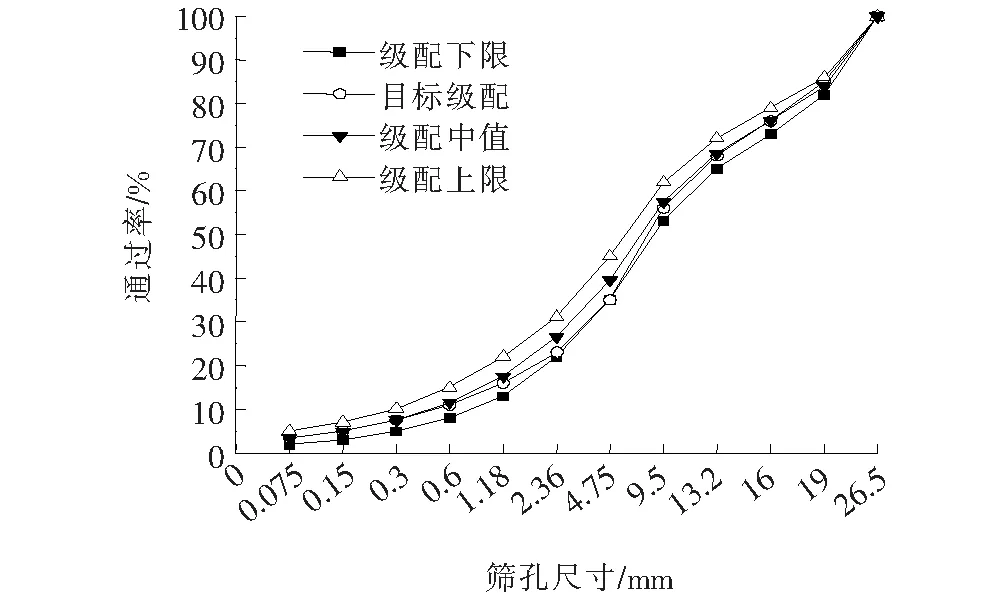
图1 水泥稳定碎石矿料级配曲线

1.2 试件成型

按照规程的试件成型方法，水泥稳定碎石采用振动压实法确定的最大干密度为2.349 g/cm3，最佳含水量为5.15%。据此，制作水泥剂量为5%的试件，其中，圆柱体试件尺寸为φ150 mm×150 mm，梁式试件的尺寸为450 mm×150 mm×150 mm。试件的成型均采用垂直振动的方法，成型后，将试件置于温度为(20±2) ℃、湿度不小于95%的标准养生室内养生。

2 强度测试分析

2.1 强度测试模型

(1) 单轴压缩强度计算公式

(1)

(2)

式中：Re为单轴压缩试件强度(MPa)；P为试件所受的破坏荷载(kN)；A为试件接触面积(mm2)；D为单轴压缩试件的直径(mm)。

(2) 四点弯曲强度计算公式

(3)

式中：Rs为抗压试件强度(MPa)；b为试件宽度(mm)；h为试件高度(mm)；l为两支点的跨距(mm)。

(3) 劈裂强度计算公式

(4)

式中：Rt为劈裂强度(MPa)。

2.2 强度试验及结果分析

将试件养生至90 d，并在强度试验前将试件置于(20±2) ℃的条件下浸水24 h，保持水面在试件顶上约2.5 cm。单轴压缩、四点弯曲和劈裂强度试验均在MTS万能材料试验机上进行。为了充分考虑水泥稳定碎石在成型和长时间养生过程中试件均质性的差异，对每种强度试验均进行15次平行测试。根据强度计算公式(1)～(4)，不同应力状态下的水泥稳定碎石强度结果如表2所示。

表2 水泥稳定碎石强度结果

由表2可知：水泥稳定碎石的3种应力强度试验结果差异性均较大。不同强度试验结果的变异系数大小排列为：四点弯曲18.74%>劈裂16.29%>单轴压缩15.92%。显然，相比于道路材料的其他性能试验结果，水泥稳定碎石强度的试验结果存在较大的离散性。然而，强度试验结果除了与试件的组成材料有关外，测试仪器和计算模型参数的精确性都会对每次强度的取值产生影响。为了系统地分析强度结果差异性的主要原因，需要对水泥稳定碎石的强度进行不确定度分析与评定。

3 强度测量不确定度的影响因素

根据不确定度的评定方法，将利用统计分析方法计算的标准不确定度称为A类评定，将无法使用统计学进行计算的不确定度统称为B类评定。平行试件的不均匀性会导致强度测量结果产生差异性，这种差异可以直接利用若干试件的强度测量结果进行统计分析，属于A类评定方法。此外，由强度的数学模型分析可知，试件尺寸和破坏荷载的测量误差是影响强度计算结果的直接影响量。其中，圆柱体试件尺寸的测量误差包括试件的高度h和直径D，梁式试件尺寸的测量误差包括高度h、宽度b和梁的跨距l。破坏荷载P的测量误差主要是由试验机的测量精度和数据采集系统的误差引起。针对由试件尺寸和试验机引入的测量不确定度，可采用B类评定方法分析。综上，不同应力状态下的强度不确定度影响因素及评定方法如表3所示。

表3 影响水泥稳定碎石强度结果测量准确性的主要因素

4 强度测量不确定度的评定

4.1 试件不均匀性引入的测量不确定度

根据表2实测的强度结果，对不同应力状态下，由试件不均匀性引入的测量不确定度采用A类评定方法。在统计方法中，采用贝赛尔公式进行计算：

(5)

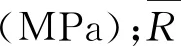
根据式(5)，在不同应力状态下，由试件不均匀性引入的强度标准不确定度分别为：单轴压缩ue(R)=0.53 MPa；四点弯曲us(R)=0.07 MPa；劈裂ut(R)=0.10 MPa。

以水泥稳定碎石强度的平均值为期望值，则因试件不均匀性引入的相对标准不确定度分别为：

由上述计算结果分析可知：不同应力状态下的水泥稳定碎石强度由试件不均匀性引入的相对不确定度大小及比较关系为：urel,s(R)=4.69%>urel,t(R)=4.07%>urel,e(R)=3.98%。结合表2对强度变异系数的分析可知，水泥稳定碎石强度由试件不均匀性引入的相对不确定度和变异系数呈正相关关系：变异系数越大，试件越不均匀，相对不确定度也就越大。并且两者的应力状态大小次序均为四点弯曲>劈裂>单轴压缩，即在水泥稳定碎石的强度试验中，四点弯曲强度受试件不均匀性的影响最显著。分析原因为：梁式试件的体积比圆柱体试件要大得多，在成型及养生过程中，影响试件强度形成的因素也更多；另外，四点弯曲试验条件相比而言也更加复杂。

4.2 强度数学模型输入量引入的测量不确定度

4.2.1 试件尺寸及梁跨距引入的测量不确定度

圆柱体试件高度h和直径D，梁试件宽度b和高度h的测量误差引起的不确定度主要是由测量工具的精度和示值误差造成的；而梁式试件在加载时，跨距l由试验装置来控制，因此梁跨距l的测量误差引起的不确定度是由试验装置的加工精度引起的。根据测量不确定度的B类评定方法，标准不确定度的计算公式为：

(6)

式中：u(x)为尺寸测量误差的标准不确定度(mm)；a为误差值的区间半宽度；k为包含因子,不同分布类型的包含因子k如表4所示。

表4 常见分布类型的k值

(1) 测量工具精度引入的不确定度

试件的尺寸均由钢直尺测得，其规定的最大允许误差为±0.1 mm，按均匀分布考虑，则由直尺精度引入的标准不确定度为：

(2) 示值误差引入的不确定度

钢直尺的最小分辨率为1 mm，按均匀分布考虑，故由示值误差引入的标准不确定度为：

测量工具精度和示值误差引起的不确定度相互独立，则梁式试件宽度的合成标准不确定度为：

以梁式试件标准宽度为期望值，则由宽度测量误差引入的相对不确定度为：

urel(b)=0.58/150=0.39%

试件高度和直径由测量误差引入的相对不确定度与宽度的分析方法相同，则试件高度和直径由测量误差引入的相对不确定度为：

urel(b)=urel(h)=urel(D)=0.58/150=0.39%

(3) 试验装置加工精度引入的不确定度

试验装置加工误差控制在±1 mm，按均匀分布考虑，则梁式试件弯曲强度由跨距误差引入的标准不确定度为：

以梁式试件试验要求的跨距为期望值，故相对不确定度为：

urel(l)=0.58/450=0.13%

4.2.2 破坏荷载测量误差引入的不确定度

根据文献[15]，破坏荷载的测量不确定度主要由MTS试验机的测量精度和计算机数据采集系统的误差引入。按B类评定方法计算，破坏荷载测量误差引入的不确定度分析如下：

(1) 试验机测量精度引入的不确定度

MTS试验机示值误差为±0.5%，采用均匀分布，则破坏荷载由试验机测量精度引入的相对不确定度为：

(2) 数据采集系统误差引入的不确定度

根据文献[15]数据采集系统的校准要求，MTS试验机的数据采集系统引入的相对不确定度为：urel(P2)=0.2%。

以上两个因素相互独立，故破坏荷载由MTS试验机引入的相对不确定度为：

5 合成标准不确定度

5.1 强度数学模型输入量的合成相对不确定度

根据测量不确定度的传播定律，当各输入量彼此独立时，计算量的合成相对不确定度可按下式计算：

(7)

(8)

式中：uc(y)为合成相对不确定度；ci为灵敏系数(或传播系数)；urel(xi)为各输入量的相对不确定度。

根据式(7)，由不同应力状态的强度数学模型输入量合成的测量不确定度计算式如下。

(1) 单轴压缩强度输入量的合成相对不确定度：

(2) 四点弯曲强度输入量的合成相对不确定度：

(3) 劈裂强度输入量的合成相对不确定度：

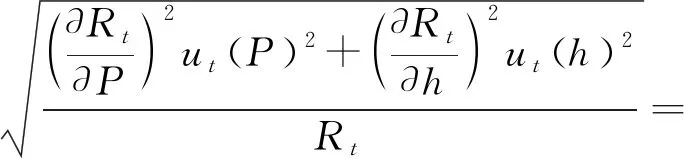
5.2 计算水泥稳定碎石强度的合成相对不确定度

由试件不均匀性和数学模型输入量的测量误差引入的不确定度相互独立，根据不确定度的传播定律，不同应力状态下的水泥稳定碎石强度的合成相对不确定度计算式如下。

(1) 单轴压缩强度的合成相对不确定度：

(2) 四点弯曲强度的合成相对不确定度：

(3) 劈裂强度的合成相对不确定度：

5.3 水泥稳定碎石强度测量不确定度汇总

根据以上对不同应力状态下的水泥稳定碎石强度测量不确定度的计算，列出水泥稳定碎石强度测量不确定度的分量汇总如表5所示。

表5 水泥稳定碎石强度测量不确定度分量汇总

由表5可知：相比其他因素对强度不确定度的影响程度，由试件不均匀性引入的不确定度贡献量:在单轴压缩强度中占比达97.7%；在四点弯曲强度中占比达98.2%；在劈裂强度中占比达99.3%。由此可知，无论何种应力状态下，水泥稳定碎石强度的不确定度主要来自试件的不均匀性。而输入量的测量误差对水泥稳定碎石强度测量不确定度的贡献占比很小，一般情况下，可以忽略不计。

6 强度的扩展不确定度及不确定度报告

扩展不确定度为合成不确定度与包含因子的乘积，按下式计算。

(9)

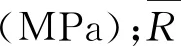
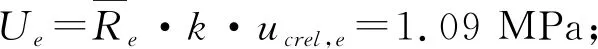
因此，不同应力状况下的水泥稳定碎石强度的扩展不确定度报告可表示为：单轴压缩强度Re=13.38 MPa,U=1.09 MPa,k=2；四点弯曲强度Rs=1.46 MPa,U=0.14 MPa,k=2；劈裂强度Rt=2.38 MPa,U=0.20 MPa,k=2。

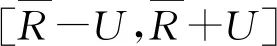
由图2可知：在不同的应力状态下，各强度由规范方法计算的平均值均位于强度区间内，而具有95%保证率的强度值均位于强度区间之下。相比于规范方法要求的强度平均值、标准差、变异系数和95%保证率值为试验结果的计算值，以基于测量不确定度理论评定方法转换的强度区间在表达上更简洁直观。

图2 不同分析方法下的水泥稳定碎石强度

一方面，强度区间包含了对强度测量试验全过程的影响范围值，即综合考虑了各种误差影响量的结果；另一方面，虽然水泥稳定碎石的扩展不确定度相对于强度均值并不大，但当测量结果位于规范临界值附近时，其结果是否合格应该考虑测量不确定度的影响范围。水泥稳定碎石强度作为道路基层设计材料的试验参数，其大小将直接影响路基设计指标的验算结果。因此，为了能充分考虑室内试验误差对路基设计的影响，建议以不利条件下，结合测量不确定度理论转换的强度区间，以区间强度下端点值为实测强度的代表值。

7 结论

测量不确定度是对测量结果质量的定量表征，在一定程度上反映了试验测量过程的误差影响大小。该文通过对水泥稳定碎石在3种应力状态下的强度试验和不确定度的分析与评定，得到以下结论：

(1) 3种应力状态下的水泥稳定碎石强度结果的变异系数越大，试件越不均匀，其相对不确定度也越大。相比于其他应力状态，四点弯曲强度受试件不均匀性引入的不确定度最大。

(2) 无论何种应力状态下，试件的不均匀性是水泥稳定碎石强度测量不确定度最主要的影响因素。一般情况下，由强度输入量引入的不确定度可忽略不计。该文评定的不同应力状态强度的不确定度报告可供同试验条件下的水泥稳定碎石强度试验参考。

(3) 水泥稳定碎石强度区间包含了试验测量误差的影响大小，可以充分反映出试验过程的复杂性及测量结果的不确定性范围。因此，强度区间在表达上更符合实际情况，相比规范方法的计算结果更加直观。

(4) 对于在规范临界值附近的强度测量结果，其是否合格应该考虑测量不确定度的影响范围。为了使水泥稳定碎石强度试验结果能提供最大保障的设计指标验算结果，建议以区间强度下端点值为实测强度的代表值。