等比数列及其前n 项和的性质与应用

◇ 陈晓明

在各级各类考试中，等比数列及其前n项和的各种性质的考查十分常见，但教材中呈现出来的显性性质较少，因此，非常有必要对等比数列及其前n项和的性质进行进一步研究、归纳、总结.同时，在解题中经常用到等比数列的相关性质，我们对它们进行归纳、总结，可让我们的解题思路更开阔.另外，研究等比数列及其前n项和的性质与应用可以类比等差数列及其前n项和的性质与应用.

“等比数列”“等比数列的前n项和”分别是人教A版教材数学《必修5》(以下简称“教材”)中第二章“数列”第2.4和2.5节内容.教材中这两节内容呈现的是知识的“学术形态”，作为数学教师，必须将其转化为“教育形态”才能让学生更容易接受，或者说能更好地备考.在各级各类考试中，对等比数列及其前n项和的各种性质的考查显得尤为突出，而教材中呈现出来的显性性质较少，因此，本文对等比数列及其前n项和的性质进行进一步研究、归纳、总结.

1 等比数列及其前n项和有关概念

1.1 等比数列的定义

一般地，如果一个数列从第2项起，每一项与它的前一项的比等于同一个常数，那么这个数列就叫作等比数列，这个常数叫作等比数列的公比，公比通常用字母q表示(q≠0).用符号语言表示等比数列为

1.2 等比数列的通项公式及其几何意义

等比数列{an}的通项公式为an＝a1qn－1，即an＝，当q＞0且q≠1时，an为n的指数型函数，此时函数图象为指数型函数图象上的孤立点.易知数列{an}为等比数列的充要条件是其通项公式an＝f(n)＝cqn(c，q为非零常数).

推广an＝amqn－m(当m＝1时即为通项公式)，其变式为

1.3 等比数列的前n项和公式及其几何意义

2 等比数列及其前n项和的性质

2.1 角码和定理

在等比数列中，若p＋q＝m＋n(p，q，m，n∈N＋)，则有apaq＝aman.特别地，

(1)当m＝n时

(2)an－kan＋k＝

另外，该定理可推广到多项的情况，如：若p＋q＋s＝m＋n＋t(p，q，m，n，s，t∈N＋)，则apaqas＝amanat.要注意的是利用角码和定理时，需要满足等式左右两边项数相同，不要出现认为a2a3＝a5始终成立的错误.

练习(1)等比数列{an}中，若a7＝10，a14＝20，则a21＝_________.

(2)在等比数列{an}中知a2a3a10a11＝36，则a5a8＝_____.

答案(1)40；(2)±6.

2.2 单调性

和等差数列相比，等比数列{an}的单调性要复杂多了.令等比数列公比为q，则

(1)当a1＞0时，若q＞1，则{an}为递增等比数列；若0＜q＜1，则{an}为递减等比数列.

(2)当a1＜0时，若q＞1，则{an}为递减等比数列；若0＜q＜1，则{an}为递增等比数列.

(3)若q＝1，则{an}为常数列，不具备单调性.

(4)若q＜0，则{an}为摆动数列，不具备单调性.

2.3 运算性质

(1)若{an}是等比数列，则数列{kan}(k≠0)，{apn＋q}(p，q∈N＋)，{|an|}均为等比数列.

(2)若{an}是等比数列，则数列均为等比数列.

推广一个等比数列各项的k次幂仍组成一个等比数列，新公比是原公比的k次幂.

(3)若{an}，{bn}都是等比数列，则数列{kan·(k，p为非零常数)均为等比数列.

(4)若{an}是等比数列，且公比q≠－1，则数列a1＋a2，a2＋a3，a3＋a4，…也是等比数列，且公比为q.(可再进行推广).

(5)若{an}是等比数列，令a1a2a3…ak＝Tk，则数列也是等比数列.

(6)若{an}是等差数列，则数列{man}(m为非零常数)是等比数列；若{an}是正项等比数列，则数列{logcan}(c为正常数且c≠1)是等差数列.

2.4 等比数列前n项和Sn的几个结论

(1)若{an}是等比数列，Sn是其前n项和，且公比q≠－1，则数列Sk，S2k－Sk，S3k－S2k，…(k∈N＋)也是等比数列，且公比q′＝qk.当q＝－1，且k为偶数时，则数列Sk，S2k－Sk，S3k－S2k，…(k∈N＋)是各项为0的常数列，不是等比数列；当q＝－1，且k为奇数时，则数列Sk，S2k－Sk，S3k－S2k，…(k∈N＋)仍为等比数列.

(2)在等比数列{an}中，当项数为偶数2n时，S偶＝qS奇；当项数为奇数2n＋1时，S奇＝a1＋qS偶.(注：S偶＝a2＋a4＋a6＋…，S奇＝a1＋a3＋a5＋…).

(3)在等比数列{an}中，

练习在等比数列{an}中，若a1＋a3＋a5＋…＋a99＝150，且公比q＝2，则数列{an}的前100项和为_________.

答案因为，所以a2＋a4＋…＋a100＝300，因此，易知数列{an}的前100项和为450.

3 应用举例

例1定义在(－∞，0)∪(0，＋∞)上的函数f(x)，如果对于任意给定的等比数列{an}，{f(an)}仍是等比数列，则称f(x)为“保等比数列函数”.现有定义在(－∞，0)∪(0，＋∞)上的如下函数：

①f(x)＝x2； ②f(x)＝2x；

③f(x)＝④f(x)＝ln|x|.

其中是“保等比数列函数”的f(x)序号为( ).

A.①② B.③④ C.①③ D.②④

简析由上述等比数列的运算性质，不难判断本题正确答案是C.

例2若数列{an}是等比数列，则下面四个数列中为等比数列的有( ).

①{can}(c为常数)；②{an＋an＋1}；③{an·an＋1}；④

A.1个 B.2个 C.3个 D.4个

对于①，若{an}是等比数列，则当c＝0时，{can}不是等比数列；对于②，若{an}是公比q＝－1的等比数列，则an＋an＋1＝0，所以{an＋an＋1}不是等比数列；对于③④，由等比数列的定义及运算性质可知其均为等比数列.故选B.

例3在等比数列{an}中，an＞0，且a2＝1－a1，a4＝9－a3，则a4＋a5的值为( ).

A.16 B.27 C.36 D.81

方法1设等比数列{an}的公比为q，由已知 得所以q2＝9，因为an＞0，所以q＝3，故a4＋a5＝q(a3＋a4)＝3×9＝27，故选B.

方法2设等比数列{an}的公比为q，由an＞0可知，q＞0.由已知得，解得q＝3或－3(舍).根据等比数列的运算性质可得a1＋a2，a2＋a3，a3＋a4，a4＋a5成等比数列，且公比为3，所以a4＋a5＝1×33＝27，故选B.

例4设{an}是各项均为正数的等比数列，bn＝log2an，b1＋b2＋b3＝3，b1b2b3＝－3，求{an}的通项公式.

设数列{an}的首项为a1，公比为q.因为b1＋b2＋b3＝3，所以log2a1＋log2a2＋log2a3＝3，即log2(a1a2a2)＝3，所以a1a2a3＝8，由角码和定理，得＝8，故a2＝2.因为b1b2b3＝－3，所以log2a1·log2a2·log2a3＝－3，故log2a1·log2a3＝－3，所以

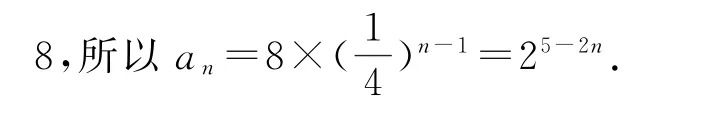
例5已知三角形的三边长度可构成等比数列，它们的公比为q，试求q的取值范围.

设三边长为a，aq，aq2(q＞0)，因为三角形两边之和大于第三边，所以由等比数列的单调性可分类讨论.

通过对比四种解题方法，可以发现方法1思路简便，但运算量过大；方法2采用特殊值法，使问题简单化，但只适用于解选择题；方法3思路略显复杂；方法4应用等比数列前n项和的性质，简化运算，且思路清晰.

上述结论及公式隐藏在教材不同的角落，同学们要注意将它们联系起来进行研究，这样才会更加清楚地认识到问题的本质，才能有新的发现，从而将知识融会贯通.同时，上述结论及公式在解题中经常用到，我们对它们进行归纳、总结，可让我们的解题思路更开阔.

等比数列是特殊的数列，更是特殊的函数，利用函数思想研究等比数列及其前n项和是解决问题的一个重要的突破口，应引起我们的重视.另外，研究等比数列及其前n项和的性质与应用可以类比等差数列及其前n项和的性质与应用.